Journal of Computer and Communications
Vol.2 No.8(2014), Article
ID:47257,11
pages
DOI:10.4236/jcc.2014.28004
Differentially-Keyed IR-UWB Signals for MA with Differential-Detection Receiver
Walid Mahmoud
Communications and Networks Engineering Department, Prince Sultan University, Riyadh, KSA
Email: wmahmoud@gmail.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 April 2014; revised 25 May 2014; accepted 17 June 2014
ABSTRACT
Noncoherent communication receivers (differential-detectors) have simple design, however, they always incur bit error rate (BER) performance loss up to 3dB compared to coherent receivers. In this paper, a differential-detector is proposed for impulse radio ultra wideband (IR-UWB) communication systems. The system employs bit-level differential phase shift keying (DPSK) combined with code division (CD) for IR-UWB signals to support multiple-access (MA). It is analyzed under additive white Gaussian noise (AWGN) corrupted by multiple-access interference (MAI) channel. Its BER performance is compared against a reference coherent receiver using MonteCarlo simulation method. A closed form expression for its average probability of error is derived analytically. Simulation results and theoretical analysis confirm the applicability of the proposed differential-detector for IR-UWB communication systems.
Keywords:Impulse-Radio Ultra-Wideband, Code Division Multiple Access, Multiple Access Interference, Bit Error Rate, Differential-Detection

1. Introduction
The federal communications commission (FCC) in USA has approved UWB technology for commercial use in February 2002 [1] . UWB signal is characterized by having a transmission bandwidth greater than 500 MHz or a signal whose bandwidth to the center frequency ratio is greater than twenty percents. The bandwidth is defined as the difference between −10 dB cut-off frequencies from the spectral peak-power value of UWB signal [2] . UWB has been accepted as an alternative physical layer for wireless personal area networks (WPANs) applications [3] . UWB communication systems depending on their propagated radio are classified as either impulseradio ultra-wideband (IR-UWB) or multi-carrier ultra-wideband (MC-UWB) [4] [5] .
Transmitted signal in IR-UWB communication systems consists of a series of short-duration pulses of nanosecond order or less transmitted at baseband [6] . Thereby the energy of the signal is spread over a broad frequency range in the available UWB spectrum from (3.1 - 10.6) GHz, with very low power spectral density. Because of this, UWB technology can coexist with other radio services, achieve high throughput, and share the spectrum for multiple-access (MA). Although IR-UWB is intended to work at baseband level, some practical systems still utilize a carrier signal [7] -[9] .
In this paper, we present a noncoherent communication system that employs bit-level DPSK modulation combined with code division (CD) on the transmitted IR-UWB signals to support multiple-access (MA). The system is analyzed under the additive white Gaussian noise (AWGN) corrupted by multiple-access interference (MAI) channel. Multiple access capability is investigated and expressed in mathematical equation as a function of active users in the system. Our proposed receiver implements differential-detection on received signal to detect the originally transmitted information bit, which is referred to as DS-DPSK. Its BER performance is compared with the BER of a reference coherent receiver reported in [10] , which is referred to as DS-PAM because it employs antipodal modulation on transmitted IR-UWB signals. Comparison results indicated that the performance of our system is slightly worse than that of DS-PAM system; however, our system has simple structure that results in less design costs and power consumption.
This paper is organized as follows. Mathematical model for the proposed system is provided in Section 2. Theoretical analysis and error probability derivation are provided in Section 3. Simulation results are presented in Section 4. Finally, the conclusion is drawn in Section 5.
2. Proposed DS-DPSK System Model
2.1. Transmitter
The transmitter in DS-DPSK system is similar to that in [10] , except that the system use bit-level differential encoding and the PAM Modulator is replaced by DPSK Modulator as shown in Figure 1.
The transmit signal for the 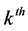 user is given by
user is given by
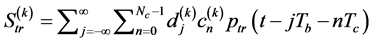 , (1)
, (1)
where 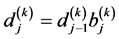 is the
is the 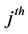 differentially encoded bit for all
differentially encoded bit for all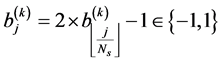 ,
, 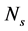 is the pulse repetition time,
is the pulse repetition time, ![]() is the used gold code sequence,
is the used gold code sequence, 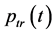 is the transmitted 2nd derivative Gaussian pulse,
is the transmitted 2nd derivative Gaussian pulse, 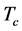 is the pulse repetition period,
is the pulse repetition period,  is the number of pulses per bit and the bit period is
is the number of pulses per bit and the bit period is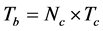 .
.
2.2. Channel
The channel is the additive white Gaussian noise (AWGN) corrupted by multiple-access interference (MAI) channel that has two sources of noise. The first source is the receiver noise, denoted as 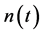 and represents the additive random thermal noise at receiver input. This noise is modeled as a white Gaussian random process that has zero-mean and variance
and represents the additive random thermal noise at receiver input. This noise is modeled as a white Gaussian random process that has zero-mean and variance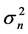 , i.e.,
, i.e., 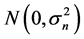 , with two-sided power spectral density equal to
, with two-sided power spectral density equal to . The second source is the MAI that represents the aggregate effect of having more than one active user in the system simultaneously. The MAI is approximated as a white Gaussian random process on the basis of central limit theorem.
. The second source is the MAI that represents the aggregate effect of having more than one active user in the system simultaneously. The MAI is approximated as a white Gaussian random process on the basis of central limit theorem.

Figure 1. DS-DPSK transmitter.
2.3. Receiver
When there are 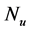 active users in the system, the received signal is given by
active users in the system, the received signal is given by
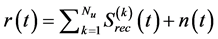 , (2)
, (2)
where 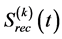 is the received signal of
is the received signal of 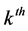 user at receiver input, and
user at receiver input, and 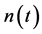 is the added receiver noise.
is the added receiver noise.
Bit-level differential encoding at transmitter side allows for bit-level differential detection at receiver side. In this scheme, the previous signaling interval (i.e., bit-period long) is used to recover the originally transmitted data bit from the current signaling interval. Therefore, receiver device should have two branches, namely branch A and branch B, to represent 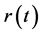 and
and 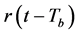 as shown in Figure 2.
as shown in Figure 2.
At receiver input each user is recognized by a unique Pseudo-Noise (PN) code. The PN Code Generator in Figure 2 exists mainly to generate the unique code for the user currently receiving data. The variable statistics at each branch, namely  and
and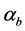 , are the result of correlating
, are the result of correlating 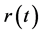 and
and 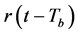 with the desired-user PN code over bit-period. Multiplying
with the desired-user PN code over bit-period. Multiplying 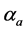 and
and 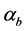 is equivalent to extracting the sign or the phase difference between the current and previous signaling intervals. The decision variable, Z, at the mixer-output is then compared against the threshold to recover the originally transmitted information bit.
is equivalent to extracting the sign or the phase difference between the current and previous signaling intervals. The decision variable, Z, at the mixer-output is then compared against the threshold to recover the originally transmitted information bit.
3. Receiver Analysis
3.1. Theoretical Analysis
In this subsection the variable statistics like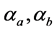 , and the decision variable Z shown in Figure 2 are analyzed, and expressed mathematically. The expression for the average probability of error in the proposed receiver is derived using the obtained mathematical expressions.
, and the decision variable Z shown in Figure 2 are analyzed, and expressed mathematically. The expression for the average probability of error in the proposed receiver is derived using the obtained mathematical expressions.
3.1.1. Branch A
Referring to Figure 2, correlator output is given by
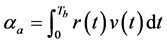 . (3)
. (3)
The assumption hereafter is that user 1 will be the desired user, and we are going to detect the ![]() data bit. In this case, the template can be defined as
data bit. In this case, the template can be defined as
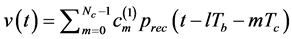 , (4)
, (4)
and the received signal after simplification is given by
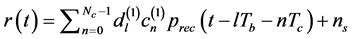 , (5)
, (5)
where 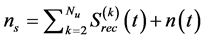 is the noise source including MAI and receiver noise
is the noise source including MAI and receiver noise , and excluding the signal of the desired user.
, and excluding the signal of the desired user. 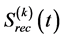 is the received signal of
is the received signal of 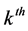 user at receiver input. Referring to (3),
user at receiver input. Referring to (3), 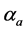 in the
in the ![]() bit-period is given by
bit-period is given by
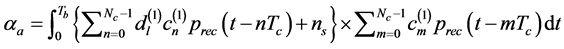 . (6)
. (6)
Let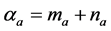 , where
, where 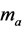 and
and ![]() are the desired signal and noise components at Branch A, respectively.
are the desired signal and noise components at Branch A, respectively.
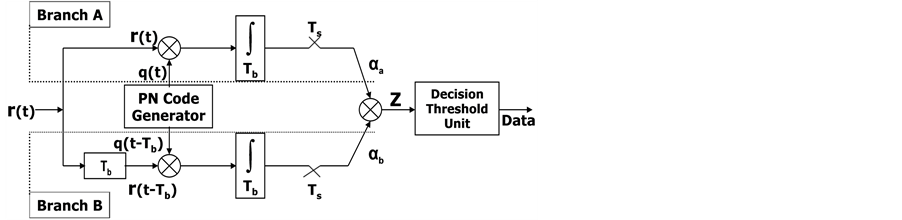
Figure 2. Proposed differential-detection MA receiver (DS-DPSK).
The desired signal component  is given by
is given by
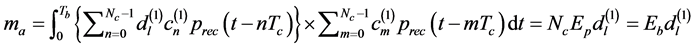 , (7)
, (7)
and the noise component ![]() is given by
is given by
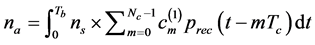 . (8)
. (8)
Therefore ![]() can be expressed as
can be expressed as
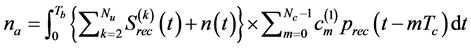 . (9)
. (9)
Furthermore, ![]() can be simplified and expressed as
can be simplified and expressed as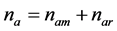 , where
, where 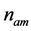 and
and 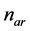 are the noise components at Branch A due to MAI and receiver noise, respectively. The noise component due to MAI,
are the noise components at Branch A due to MAI and receiver noise, respectively. The noise component due to MAI,  , is given by
, is given by
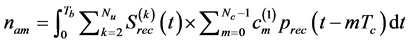 . (10)
. (10)
After simplifying (10) above, 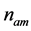 can be expressed as
can be expressed as
 , (11)
, (11)
where 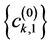 is the synchronous cross-correlation function between the desired and interfering users during the
is the synchronous cross-correlation function between the desired and interfering users during the ![]() bit-period. Now the expression for the noise component due to receiver noise,
bit-period. Now the expression for the noise component due to receiver noise,  , is given by
, is given by
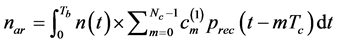 . (12)
. (12)
Under the assumption in [11] ,  has Gaussian distribution with zero-mean and variance
has Gaussian distribution with zero-mean and variance 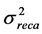 that is given by
that is given by
![]() . (13)
. (13)
Thus, the variable statistic 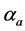 for Branch A is given by
for Branch A is given by
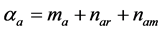 . (14)
. (14)
The obtained variable statistic will assist in deriving the final expression for the average probability of error in the proposed receiver.
3.1.2. Branch B
Due to similarity of derivations with Branch A, except for the bit-period delay that should be considered, only necessary derivations relevant to Branch B are included here. By following similar steps, the variable statistic 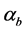 is given by
is given by
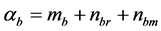 , (15)
, (15)
where the right-hand side terms are the desired signal, receiver noise and MAI components in Branch B, respectively. The desired signal component 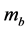 is given by
is given by
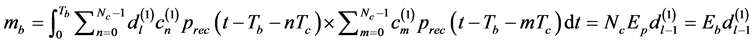 . (16)
. (16)
The noise component due to receiver noise, 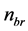 , is given by
, is given by
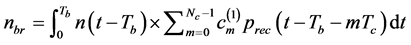 . (17)
. (17)
Similar to 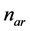 in (12),
in (12), 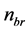 has Gaussian distribution with zero-mean and variance
has Gaussian distribution with zero-mean and variance 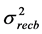 that is given by
that is given by
![]() . (18)
. (18)
The noise component due to MAI, 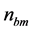 , is given by
, is given by
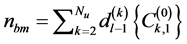 , (19)
, (19)
where 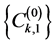 is the cross-correlation function between the desired and interfering users during the
is the cross-correlation function between the desired and interfering users during the 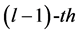 bit-period.
bit-period.
3.2. Error Probability Derivation
The randomness of the used PN code sequences with the existence of more than one active-user concurrently in the system permits the approximation of MAI terms, 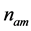 in (11) and
in (11) and  in (19) as Gaussian random processes [12] . Therefore, the variable statistic
in (19) as Gaussian random processes [12] . Therefore, the variable statistic 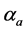 can be expressed as
can be expressed as
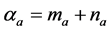 , (20)
, (20)
where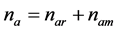 , and the variable statistic
, and the variable statistic 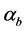 can be expressed as
can be expressed as
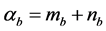 , (21)
, (21)
where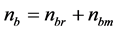 . Referring to Figure 2, the decision variable Z is equal to the multiplication of the variable statistics
. Referring to Figure 2, the decision variable Z is equal to the multiplication of the variable statistics 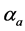 and
and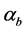 . Assuming that the data bit 1 is transmitted, then, the current and previous bits of DPSK signal are the same, hence
. Assuming that the data bit 1 is transmitted, then, the current and previous bits of DPSK signal are the same, hence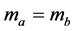 . Therefore, Z after simplification can be expressed as
. Therefore, Z after simplification can be expressed as
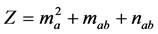 , (22)
, (22)
where 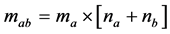 and
and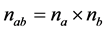 . If the desired signal component
. If the desired signal component 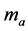 in (7) is squared, then we have
in (7) is squared, then we have
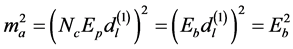 . (23)
. (23)
Note that receiver noise 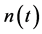 is modeled as AWGN process with zero-mean (DC power) and variance
is modeled as AWGN process with zero-mean (DC power) and variance 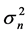
(AC power) that is equal to the spectral (total) power of this process. Therefore, 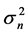 is equal to
is equal to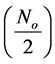 . Substituting the value of
. Substituting the value of 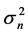 in (13), the expected value for
in (13), the expected value for 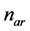 is given by
is given by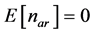 , and its variance
, and its variance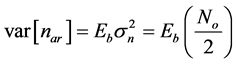 . The expected value for
. The expected value for 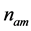 is given by
is given by 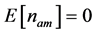 and its variance
and its variance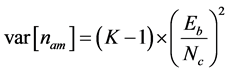 . After approximating MAI term with a Gaussian random process, and considering the effect of other active users in the system, the statistical value for the total noise at Branch A,
. After approximating MAI term with a Gaussian random process, and considering the effect of other active users in the system, the statistical value for the total noise at Branch A, ![]() , is given by
, is given by
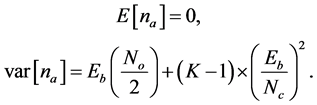 (24)
(24)
Since ![]() and
and ![]() expected to have similar statistical values due to randomness and independence of Gaussian processes, the new process is the sum of their statistics. Therefore,
expected to have similar statistical values due to randomness and independence of Gaussian processes, the new process is the sum of their statistics. Therefore, 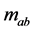 has zero-mean expected value and variance given by
has zero-mean expected value and variance given by
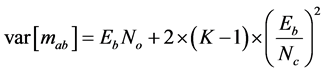 . (25)
. (25)
Statistical values for 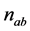 term in (22) are derived using Shannon’s sampling theorem [13] . Thus, the variable
term in (22) are derived using Shannon’s sampling theorem [13] . Thus, the variable 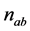 can be expressed as
can be expressed as
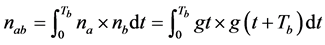 , (26)
, (26)
where 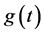 is a Gaussian random process with zero-mean and variance
is a Gaussian random process with zero-mean and variance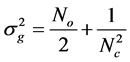 , which has autocorrelation function that is given by
, which has autocorrelation function that is given by
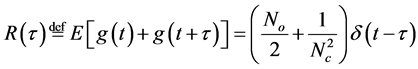 . (27)
. (27)
The sampled version of 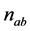 can be expressed as
can be expressed as
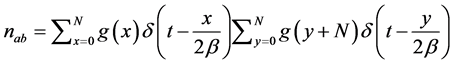 , (28)
, (28)
where 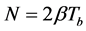 is the number of independent samples per bit, and
is the number of independent samples per bit, and 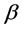 is the bandwidth of the 2nd derivative Gaussian pulse. Both
is the bandwidth of the 2nd derivative Gaussian pulse. Both 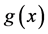 and
and 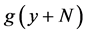 are independent and identically distributed (i.i.d) samples from the sampled version of the Gaussian process. Each sample has zero-mean and variance equal to
are independent and identically distributed (i.i.d) samples from the sampled version of the Gaussian process. Each sample has zero-mean and variance equal to 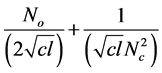 as a result of energy normalization, where
as a result of energy normalization, where ![]() is the length of the used PN code sequence. Because the bit-period
is the length of the used PN code sequence. Because the bit-period 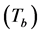 is much greater than the sampling-period
is much greater than the sampling-period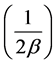 , we use the following approximation
, we use the following approximation
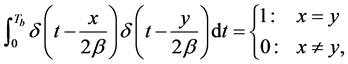 (29)
(29)
thus 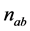 can be further simplified and is given by
can be further simplified and is given by
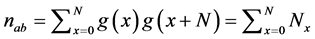 , (30)
, (30)
when![]() . Therefore, the statistics for
. Therefore, the statistics for 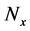 is given by
is given by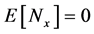 , and
, and
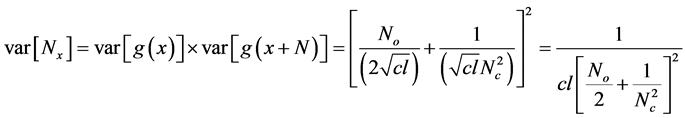 .
.
Because each sample has Gaussian distribution, the sum of the entire N independent samples also has Gaussian distribution based on central limit theorem. Therefore, 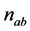 has Gaussian distribution with zero-mean expected value and variance given by
has Gaussian distribution with zero-mean expected value and variance given by
 , (31)
, (31)
after including the effect of other active users in the system. The signal-to-noise ratio 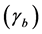 is given by
is given by
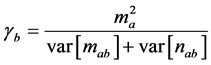 . (32)
. (32)
Substitute Equations (23), (25) and (31) in (32), the analytical expression for ![]() is given by
is given by
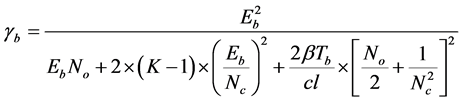 . (33)
. (33)
Substitute ![]() in the known expression for the average probability of error using DPSK receiver in AWGN channel we have
in the known expression for the average probability of error using DPSK receiver in AWGN channel we have
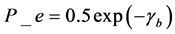 , (34)
, (34)
which is the analytical average probability of error in the proposed receiver.
4. Simulation Results
Simulation results for DS-DPSK (proposed) and DS-PAM (reference) systems using Matlab are presented in this section. Simulation parameters in both systems are identical in order to have fair and unbiased comparisons. The used 2nd derivative Gaussian pulse is given by
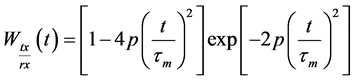 , (35)
, (35)
with pulse width 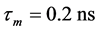 and pulse period
and pulse period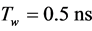 . The length of used gold sequences cl = 7 and pulse repetition period
. The length of used gold sequences cl = 7 and pulse repetition period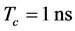 . Thus, the expected data rate for the proposed system is
. Thus, the expected data rate for the proposed system is 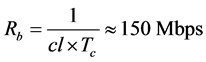
per user. In both systems the interferers are 1, 2 and 3 such that the total number of active users in the system is 4 users.
4.1. Proposed vs Reference
Performance comparison between DS-DPSK and DS-PAM receivers for the required SNR vs BER for different number of active users in the system is shown in Figure 3.
Because any communications receiver capable of achieving BER performance level 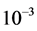 is considered functional receiver, SNR values for different number of active users at this level in both receivers are used as the
is considered functional receiver, SNR values for different number of active users at this level in both receivers are used as the
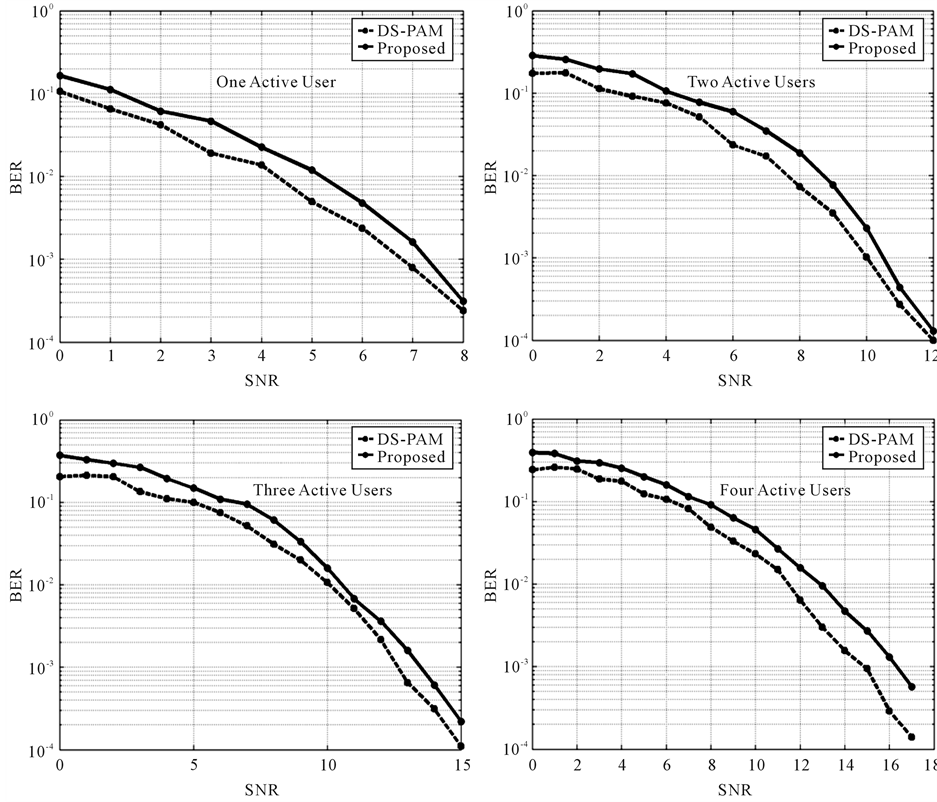
Figure 3. BER vs SNR (DS-PAM & DS-DPSK receivers).
comparison base. Such SNR values are extracted from Figure 3 and tabulated in Table 1 along with the difference and percentage difference (%PD) values.
From Figure 3, BER performance for same SNR values of proposed system is slightly worse than that of DS-PAM system. It is known in the literature that coherent (DS-PAM) receivers are superior in terms of BER performance compared to noncoherent (DS-DPSK) receivers as a result of demodulation process. In such receivers, the carrier used for demodulation at receiver side is in phase and frequency synchronism with the carrier used for modulation at transmitter side. This requires some sophisticated circuitry such as the phase-locked loop circuit, which is not a requirement for noncoherent receivers. Thus, coherent receivers are rendered complex from design perspective, costly and consume extra power. However, noncohenret receivers are known to be simple in their design, less costly and consume less power with BER performance degradation up to 3 dB compared to coherent receivers.
From Table 1, for the case of four active users in both systems, it is shown that the maximum increase in SNR required to achieve 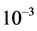 BER using DS-DPSK receiver is 1.2 dB. Since this value is less than 3 dB—the expected increase in SNR as a result of using noncoherent receivers such as differential detectors, this renders our proposed receiver a practical IR-UWB differential-detector.
BER using DS-DPSK receiver is 1.2 dB. Since this value is less than 3 dB—the expected increase in SNR as a result of using noncoherent receivers such as differential detectors, this renders our proposed receiver a practical IR-UWB differential-detector.
The slight performance improvement in the proposed system is the result of using gold code sequences in conjunction with DPSK modulation. Gold code sequences have noise-like behavior responsible in general for improving multiple-access capability of communication systems, and in particular, in improving spectral properties of the transmitted DPSK signal. In addition, working principle of DS-DPSK receiver in using template signal that experienced the same channel effects is another factor in improving its performance.
4.2. Efficiency of DS-DPSK
SNR versus BER graphs for the case of having 1, 2, 3 and 4 active users in the proposed system are shown in Figure 4. The behavior of these graphs has motivated the definition of a new performance metric, which is referred to as multiple-access efficiency (MAE), which is intended to test the efficiency of DS-DPSK as multipleaccess receiver.
Referring to Figure 4, one can see convergence in distance among the graphs in the figure and such convergence is more among the graphs representing higher number of active users in the system. MAE metric is the mathematical expression that represents the inverse of this convergence in percentage. It reflects the required increase in SNR values as a result of gradual increase in the number of active users in the system. MAE metric is given by
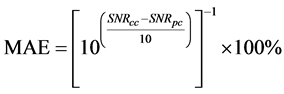 , (36)
, (36)
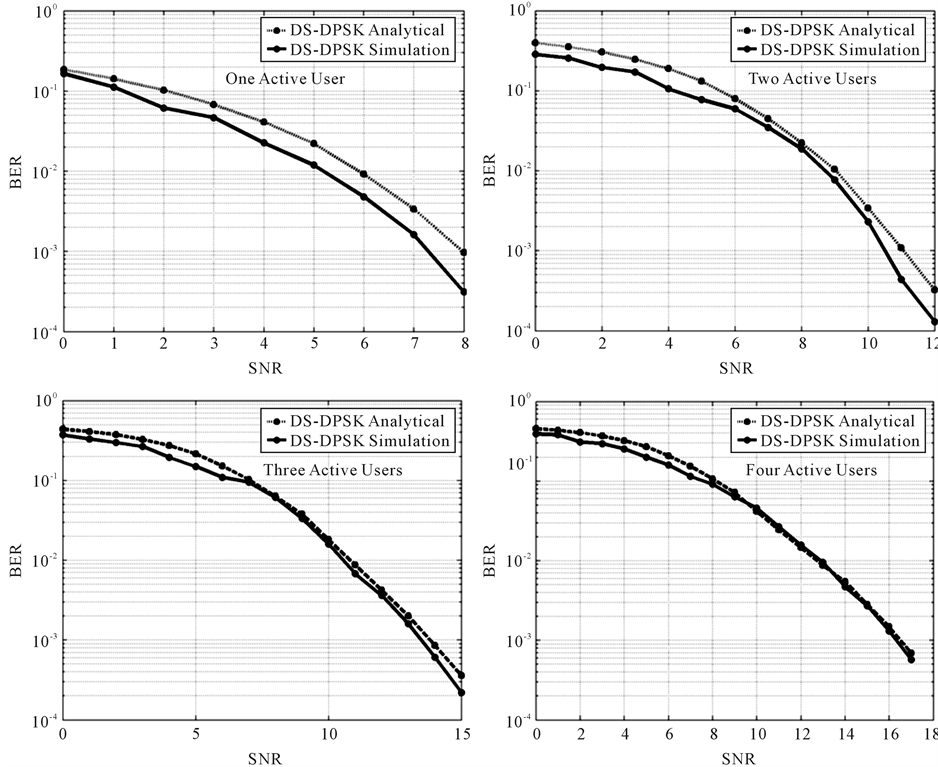
where Figure 4, if the movement is from the intersection point on the single-user graph to the intersection point on the two-users Table 1. Performance comparison DS-PAM & DS-DPSK. aPercentage difference. Figure 4. BER vs SNR (MAE of DS-DPSK receiver). graph, then The slight gradual increase in SNR values above indicates that DS-DPSK receiver is capable of handling the increase in the number of active users in the system as long as MAE not reached 100% value. This performance metric has confirmed the feasibility of the proposed system to support multiple-access. MAE metric can be used to define the upper bound for the required increase in SNR, especially when it approaches 100% value. At this value, the maximum number of active users that DS-DPSK system can support is also approached. 4.3. Analysis vs Simulation Results Comparison between analytical and simulation results for different number of active users in the proposed system is shown in Figure 5. From Figure 5, the obtained simulation results are in good match with the derived analytical results represented by the mathematical expressions describing DS-DPSK system. In other words, both graphs for each case of having difference number of active users are close to each other and change in tandem. Thus, the comparison confirmed the correctness of the followed analytical methods and the derived mathematical expressions presented herein. The small gap between graphs of one-active user in the system is the result of approximating MAI as Gaussian random process. Based on central limit theorem, this approximation becomes more valid as the number of active users in the system increases, which is evident on the graphs for more active users in the system. 5. Conclusions In this paper a noncoherent IR-UWB differential-detector (DS-DPSK) that supports multiple-access was proposed. The proposed system was analyzed under AWGN corrupted by multiple-access interference channel. Closed-form expression for the average probability of error in the proposed system was derived analytically. It is compared against a reference coherent receiver (DS-PAM) for BER performance for the cases of having 1, 2, 3 and 4 active users in the system using Matlab based on Monte-Carlo simulation method. Its capability to support multiple users was investigated and new multiple-access efficiency metric was defined. Simulation results were in good match with the derived analytical expressions describing our proposed system. Despite its slight BER performance loss as a noncohenret receiver relative to DS-PAM coherent receiver, its performance relative to other differential-detectors and its simple structure, which yields less design costs and power consumption, are the major advantages. Thus, it is a suitable IR-UWB communication system that supports multiple-access. Figure 5. Analysis vs simulation results (DS-DPSK receiver). Given the fact that mathematical analysis and simulation results confirmed the applicability of our proposed system, a possible future work is to devise other mechanisms to further improve its BER performance. Acknowledgements The author would like to warmly thank peer reviewers for their help in reviewing this manuscript. References and
and 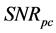 are defined as follows. By drawing a horizontal line at
are defined as follows. By drawing a horizontal line at 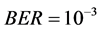 in
in 
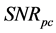 is the value of the first point and
is the value of the first point and 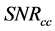 is the value of the second point. Proceeding in this way while moving from graph 2 to graph 3, and from graph 3 to graph 4, respectively, the calculated MAE values are 45.7%, 49%, and 56.5%.
is the value of the second point. Proceeding in this way while moving from graph 2 to graph 3, and from graph 3 to graph 4, respectively, the calculated MAE values are 45.7%, 49%, and 56.5%.