ABSTRACT

This article is devoted to obtaining sufficient conditions for the completion of pursuit for control systems of fractional order described with divided dynamics. The results are illustrated on model examples of gaming problems with a simple matrix and separated fractional-order motions.

Keywords:

Equations, Control Systems, Differential Game, Derivative Kaputo, Persecution, Evasion, Terminal Set

1. Introduction

At the present time, there is a noticeable increase in the attention of researchers to fractional calculus. The development of the theory of equations with derivatives of fractional order is stimulated by the development of the theory of differential equations of the whole order. The role of fractional calculus in the theory of equations of mixed type is well known, in the theory of problems with displacement, in the theory of degenerate equations. In addition, equations of fractional order, essentially supplementing the picture of the general theory of differential equations, can reveal a connection between phenomena that, remaining within the framework of integer differentiation, appear to be independent. The dynamics of systems described by differential equations of fractional order is an object of study of specialists from about the middle of the 20^th century [1] . In the middle 1970 years, F. Mainardi and M. Caputo have shown that the use of differential equations of fractional order for constructing models in problems of the thermo baric elasticity is more adequate from physical considerations and allows more accurately reproducing experimentally observed data in calculations. The study of dynamical systems of fractional order with control is actively developing in the last 10 years [2] . The growing interest in these areas is due to two main factors. First, by the middle of the last century, the mathematical foundations of fractional integro-differential calculus and the theory of differential equations of fractional order were developed [3] . Approximately at the same time, the methodology of applying fractional calculus in applied problems began to evolve, and numerical methods for calculating integrals and fractional derivatives began to develop. Secondly, in fundamental and applied physics, by that time, a significant volume of results was accumulated that showed the necessity of using the apparatus of fractional calculus for an adequate description of a number of real systems and processes [4] . As examples of real systems, we mention electrochemical cells, capacitors with fractal electrodes, viscoelastic media. These systems have, as a rule, non-trivial physical properties, useful from a practical point of view. For example, the irregular structure of the electrodes in the capacitors allows them to reach a much higher capacitance, and the use of electrical circuits with elements having a fractional-power transfer type provides more flexible tuning of the fractional order controllers used in modern control systems [5] [6] [7] .

At the present time, under the influence of rapid scientific and technical progress, fractional calculus has turned into a powerful scientific direction, including both fundamental and applied research. This is due to the need to more accurately describe the physical systems and processes that have become objects of interest of modern researchers. The distinguishing features of such systems and processes are their non-local character and the phenomenon of memory. For example, this applies to micro and nanostructured media, deterministic and chaotic including “fractal-chaotic” processes in nature and engineering.

In addition to research in the field of modeling fractional dynamical systems, research in management problems such as differential games has been actively developed in recent years. The present article is devoted to obtaining sufficient conditions for the completion of pursuit for differential games of fractional order, described with divided dynamics [8] - [15] .

2. Methods

Let the movement of the first player, whom we call the pursuer, be described by equation

$D^{\alpha }x=Ax+u,x\in R^{m_1}$ (1)

where $D^{\alpha }$ ―operator of fractional differentiation of order $\alpha$ , $n_1-1<\alpha <n_1$ , $n_1\in \mathbb{N}$ , $t\in \left[0,T\right]$ , $A$ ― $m_1\times m_1$ -constant matrix. The movement of the second player, which we will call escaping, is given by equation

$D^{\beta }y=By+\upsilon ,y\in R^{m_2}$ (2)

where $D^{\beta }$ ―operator of fractional differentiation of order $\beta$ , $n_2-1<\beta <n_2$ , $n_2\in \mathbb{N}$ , $t\in \left[0,T\right]$ , $B$ ― $m_2\times m_2$ constant matrix, $u,\upsilon$ ―control parameters, $u$ ―controlling parameter of the pursuer, $u\in P\subset R^{m_1}$ , $\upsilon$ ―the controlling parameter of the evading player, $\upsilon \in Q\subset R^{m_2}$ , $P$ and $Q$ ―compacts. The fractional derivative will be understood in the sense of Caputo [16] [17] [18] [19] [20] .

We recall that the fractional derivative of order $\gamma ,\left(n-1<\gamma <n,n\in {\rm N}\right)$ from sometimes n continuously differentiable function $z\left(t\right),z:R_{+}\to R^m$ in Caputo’s sense is defined by the expression

$D^{\gamma }z\equiv D^{\left(\gamma \right)}z\left(t\right)=\frac{1}{\Gamma \left(n-\gamma \right)}{\displaystyle \underset{0}{\overset{t}{\int }}\frac{z^{\left(n\right)}\left(\tau \right)}{{\left(t-\tau \right)}^{\gamma -n+1}}\text{d}\tau .}$ (3)

where $\Gamma (\cdot )$ ―gamma-function, which is defined as follows $\Gamma \left(\theta \right)={\displaystyle \underset{0}{\overset{\infty }{\int }}{t}^{\theta -1}{\text{e}}^{-t}\text{d}t}$ . The main property of the gamma function is expressed by the reduction formula $\Gamma \left(\theta +1\right)=\theta \Gamma \left(\theta \right)$ . If $\theta$ ―positive integer, than $\Gamma \left(\theta \right)=\left(\theta -1\right)!$ ; $\Gamma \left(\theta +\frac{1}{2}\right)=\frac{1\cdot 3\cdots \left(2\theta -1\right)}{2^{\theta }}\sqrt{\text{π}}$ . When $0<\theta <1$ we have formula $\Gamma \left(\theta \right)\Gamma \left(1-\theta \right)=\frac{\text{π}}{\sin \left(\text{π}\theta \right)}$ .

To define a terminal set, we introduce the notation $s\left(s\le \min \left(m_1,m_2\right)\right)$ , $M^1=M_0^1+M_1$ , $M_0^1\subset R^{s_1}$ , $L_1\times M_0^1=R^{s_1}$ and $M^2=M_0^2+M_1$ , $M_0^2\subset R^{s_2}$ , $L_2\times M_0^2=R^{s_2}$ . Across ${\Pi }_1$ , ${\Pi }_2$ , denote operators orthogonal to the projections respectively from $R^{m_1}$ on $L_1$ and from $R^{m_2}$ on $L_2$ and пусть $M=\left\{\left(x;y\right),x\in R^{m_1},y\in R^{m_2}:{\Pi }_{1}x-{\Pi }_{2}y\in M_1\right\}$ . The game is considered to be over, if the conditions are fulfilled. The aim of the pursuing player is to withdraw $\left(x;y\right)$ on the set M, the escaping player tries to prevent it.

Definition. We say that a differential game (1)-(3) can be completed from the initial position $x^0=\left(x_0^0,x_1^0,x_2^0,x_3^0,\cdots ,x_{n_1-1}^0\right)$ , $y^0=\left(y_0^0,y_1^0,y_2^0,\cdots ,y_{n_2-1}^0\right)$ during $T=T\left(x^0,y^0\right)$ , if there exists a measurable function $u\left(t\right)=u\left(z_0,\upsilon \left(t\right)\right)\in P$ , $t\in \left[0,T\right]$ , that the solutions of equations

$D^{\alpha }x=Ax+u\left(t\right),x\in R^{m_1},n_1-1<\alpha <n_1,x\left(0\right)=x^0,$ (4)

$D^{\beta }y=By+\upsilon \left(t\right),y\in R^{m_2},n_2-1<\beta <n_2,y\left(0\right)=y^0,$ (5)

satisfies the condition $\left(x;y\right)\in M$ , those ${\Pi }_{1}x-{\Pi }_{2}y$ belongs to the set $M_1$ in the moment $t=T$ for any measurable functions $\upsilon \left(t\right),\upsilon \left(t\right)\in Q$ , $0\le t\le T$ .

3. Formulation of Main Results

We now turn to the formulation of the main results. Let $E_{\eta }\left(G;\mu \right)={\displaystyle \sum _{k=0}^{\infty }\frac{G^k}{\Gamma \left(k{\eta }^{-1}+\mu \right)}}$

-generalized Mittag-Lefler matrix function [1] , where $\eta >0$ , $\mu \in ℂ$ ( $ℂ$ ―set of complex numbers) and $G$ ―an arbitrary square matrix of order m. We consider the dynamical system (1)-(3) with the initial conditions

$x^{\left(k\right)}\left(0\right)=x_k^0,k=0,1,\cdots ,n_1-1,y^{\left(l\right)}\left(0\right)=y_l^0,l=0,1,\cdots ,n_2-1.$ (6)

Then the solution of Equations ((4), (5)) with initial conditions (6) has the form

$x\left(t\right)={\displaystyle \sum _{k=0}^{n_1-1}{t}^k{E}_{\frac{1}{\alpha }}\left(A{t}^{\alpha };k+1\right)x_k^0}+{\displaystyle \underset{0}{\overset{t}{\int }}{\left(t-\tau \right)}^{\alpha -1}{E}_{\frac{1}{\alpha }}\left(A{\left(t-\tau \right)}^{\alpha };\alpha \right)u\left(\tau \right)d\tau }.$ (7)

$y\left(t\right)={\displaystyle \sum _{l=0}^{n_2-1}{t}^l{E}_{\frac{1}{\beta }}\left(B{t}^{\beta };l+1\right)y_l^0}+{\displaystyle \underset{0}{\overset{t}{\int }}{\left(t-\tau \right)}^{\beta -1}{E}_{\frac{1}{\beta }}\left(B{\left(t-\tau \right)}^{\beta };\beta \right)\upsilon \left(\tau \right)\text{d}\tau }.$ (8)

For $r\ge 0$ , define $\widehat{u}\left(r\right)={\Pi }_1{t}^{\alpha -1}{E}_{\frac{1}{\alpha }}\left(A{t}^{\alpha };\alpha \right)P$ , $\widehat{\upsilon }\left(r\right)={\Pi }_2{t}^{\beta -1}{E}_{\frac{1}{\beta }}\left(B{t}^{\beta };\beta \right)Q$ , $\widehat{w}\left(r\right)=\widehat{u}\left(r\right)\frac{*}{}\widehat{\upsilon }\left(r\right)$ ;

$W\left(\tau \right)={\displaystyle \underset{0}{\overset{\tau }{\int }}\widehat{w}\left(r\right)\text{d}r},\tau >0,W_1\left(\tau \right)=-M_1+W\left(\tau \right).$ (9)

For convenience, we introduce the notation $h_x\left(x^0,t\right)={\displaystyle \sum _{k=0}^{n_1-1}{t}^k{E}_{\frac{1}{\alpha }}\left(A{t}^{\alpha };k+1\right)x_k^0}$ , $h_y\left(y^0,t\right)={\displaystyle \sum _{l=0}^{n_2-1}{t}^l{E}_{\frac{1}{\beta }}\left(B{t}^{\beta };l+1\right)y_l^0}$ .

Theorem 1. If in the game (1)-(3) for some $\tau ={\tau }_1$ , the inclusion

$-{\Pi }_1{h}_x\left(x^0,\tau \right)+{\Pi }_2{h}_y\left(y^0,\tau \right)\in W_1\left(\tau \right)$ (10)

then from the initial position $x^0,y^0$ you can complete the pursuit of time $T={\tau }_1$ .

Now suppose that $\omega$ ―an arbitrary partition of the interval $\left[0,\tau \right]$ , $\omega =\left\{0=t_0<t_1<\cdots <t_p=\tau \right\}$ , $i=1,2,\cdots ,p$ , and $A_0=-M_1$ ,

$\begin{array}{l}{A}_i\left(M_1,\tau \right)=\left(A_{i-1}\left(M_1,\tau \right)+{\displaystyle \underset{t_{i-1}}{\overset{t_i}{\int }}{\Pi }_1{r}^{\alpha -1}{E}_{\frac{1}{\alpha }}\left(A{r}^{\alpha };\alpha \right)P\text{d}r}\right)\\ \frac{*}{}{\displaystyle \underset{t_{i-1}}{\overset{t_i}{\int }}{\Pi }_2{r}^{\beta -1}{E}_{\frac{1}{\beta }}\left(B{r}^{\beta };\beta \right)Q\text{d}r},i=1,2,\cdots ,p,\\ W_2\left(\tau \right)={\displaystyle \underset{\omega }{\cap }{A}_i}\left(M_1,\tau \right).\end{array}$ (11)

Theorem 2. If in the game (1)-(3) for some $\tau ={\tau }_2$ , the inclusion,

$-{\Pi }_1{h}_x\left(x^0,\tau \right)+{\Pi }_2{h}_y\left(y^0,\tau \right)\in W_2\left(\tau \right)$ (12)

then from the initial position $x^0,y^0$ you can complete the pursuit of time $T={\tau }_2$ .

We denote by $\widehat{w}\left(r,\tau \right)$ a bunch of $\left[-\frac{1}{\tau }{M}_1+\widehat{u}\left(r\right)\right]\frac{*}{}\widehat{\upsilon }\left(r\right)$ defined for all $r\ge 0$ , $\tau >0$ . Consider the integral

$W_3\left(\tau \right)={\displaystyle \underset{0}{\overset{\tau }{\int }}\widehat{w}\left(r,\tau \right)\text{d}r}.$ (13)

Theorem 3. If in the game (1)-(3) for some $\tau ={\tau }_3$ , the inclusion

$-{\Pi }_1{h}_x\left(x^0,\tau \right)+{\Pi }_2{h}_y\left(y^0,\tau \right)\in W_3\left(\tau \right)$ (14)

then from the initial position $x^0,y^0$ you can complete the pursuit of time $T={\tau }_3$ .

4. Proof of Theorems

Proof of Theorem 1. There are two possible cases:1) ${\tau }_1=0$ ; 2) ${\tau }_1>0$ . Case 1) is trivial, since when ${\tau }_1=0$ from (9) and inclusion (10) we have $-{\Pi }_1{h}_x\left(x^0,0\right)$ $+{\Pi }_2{h}_y\left(y^0,0\right)\in -M_1$ and ${\Pi }_1{x}_0^0-{\Pi }_2{y}_0^0\in M_1$ , which is equivalent to including $\left(x^0;y^0\right)\in M$ . Now let the case 2) ${\tau }_1>0$ . By the conditions of the theorem (10)

$-{\Pi }_1{h}_x\left(x^0,{\tau }_1\right)+{\Pi }_2{h}_y\left(y^0,{\tau }_1\right)\in W_1\left({\tau }_1\right)$ , then there are vectors $d\in M_1$ и $w\in {\displaystyle \underset{0}{\overset{{\tau }_1}{\int }}\widehat{w}\left(r\right)\text{d}r}$ such that (show (9), (10)) $d+w=-{\Pi }_1{h}_x\left(x^0,{\tau }_1\right)+{\Pi }_2{h}_y\left(y^0,{\tau }_1\right)$ . Further, in accordance with the definition of the integral ${\displaystyle \underset{0}{\overset{{\tau }_1}{\int }}\widehat{w}\left(r\right)\text{d}r}$ there exists a summable function $w\left(r\right),0\le r\le {\tau }_1$ , $w\left(r\right)\in \widehat{w}\left(r\right)$ , when $w={\displaystyle \underset{0}{\overset{{\tau }_1}{\int }}w\left(r\right)\text{d}r}$ . Taking this equality into account, we consider the equation

$\begin{array}{l}{\Pi }_1{\left({\tau }_1-t\right)}^{\alpha -1}{E}_{\frac{1}{\alpha }}\left(A{\left({\tau }_1-t\right)}^{\alpha };\alpha \right)u-{\Pi }_2{\left({\tau }_1-t\right)}^{\beta -1}{E}_{\frac{1}{\alpha }}\left(B{\left({\tau }_1-t\right)}^{\beta };\beta \right)\upsilon \\ =w\left({\tau }_1-t\right)\end{array}$ (15)

Relatively $u\in P$ for fixed $t\in \left[0,{\tau }_1\right]$ and $\upsilon \in Q$ . As $w\left(r\right)\in \widehat{w}\left(r\right)$ , then Equation (15) has a solution. From all solutions of (15) we choose the smallest in the lexicographic sense and denote it by $u\left(t,\upsilon \right)$ . Function $u\left(t,\upsilon \right),0\le t\le {\tau }_1,\upsilon \in Q$ , It is Lebesgue measurable with respect to and Borel measurable in $\upsilon$ [8] . Therefore, for any measurable function $\upsilon =\upsilon \left(t\right),0\le t<\infty ,\upsilon \left(t\right)\in Q$ , function $u\left(t,\upsilon \left(t\right)\right),$ $0\le t\le {\tau }_1$ , is a Lebesgue measurable function [7] . We set $u\left(t\right)=u\left(t,\upsilon \left(t\right)\right),$ $0\le t\le {\tau }_1$ and show that with this method of controlling the parameter, u the trajectory $z\left(u(\cdot ),\upsilon (\cdot ),z_0\right)$ falls on the set M for a time not exceeding $T={\tau }_1$ .

Indeed, according to (15), for the solution of $x\left(t\right),y\left(t\right),0\le t<\infty$ , equations

$D^{\alpha }x=Ax+u\left(t\right),x^{\left(k\right)}\left(0\right)=x_k^0,k=0,1,\cdots ,n_1-1$ (16)

$D^{\beta }y=By+\upsilon \left(t\right),y^{\left(l\right)}\left(0\right)=y_l^0,l=0,1,\cdots ,n_2-1$ (17)

in view of (7), (8), (16), (17) we have [1]

$\begin{array}{l}-{\Pi }_{1}x\left({\tau }_1\right)+{\Pi }_{2}y\left({\tau }_1\right)\\ =-{\Pi }_1{h}_x\left(x^0,{\tau }_1\right)+{\Pi }_2{h}_y\left(y^0,{\tau }_1\right)-{\displaystyle \underset{0}{\overset{{\tau }_1}{\int }}[{\Pi }_1{\left({\tau }_1-t\right)}^{\alpha -1}{E}_{\frac{1}{\alpha }}\left(A{\left({\tau }_1-t\right)}^{\alpha };\alpha \right)u\left(t\right)}\\ -{\Pi }_2{\left({\tau }_1-t\right)}^{\beta -1}{E}_{\frac{1}{\alpha }}\left(B{\left({\tau }_1-t\right)}^{\beta };\beta \right)\upsilon \left(t\right)]\text{d}t\\ =-{\Pi }_1{h}_x\left(x^0,{\tau }_1\right)+{\Pi }_2{h}_y\left(y^0,{\tau }_1\right)-{\displaystyle \underset{0}{\overset{{\tau }_1}{\int }}w\left({\tau }_1-t\right)\text{d}t}=-d+w-{\displaystyle \underset{0}{\overset{{\tau }_1}{\int }}w\left({\tau }_1-t\right)\text{d}t}\\ =-d+{\displaystyle \underset{0}{\overset{{\tau }_1}{\int }}w\left(r\right)\text{d}r}-{\displaystyle \underset{{\tau }_1}{\overset{0}{\int }}w\left(r\right)\text{d}r}=-d-{\displaystyle \underset{0}{\overset{{\tau }_1}{\int }}w\left(r\right)\text{d}r}+{\displaystyle \underset{0}{\overset{{\tau }_1}{\int }}w\left(r\right)\text{d}r=}-d=-M_1\end{array}$

${\Pi }_{1}x\left({\tau }_1\right)-{\Pi }_{2}y\left({\tau }_1\right)=d\in M_1,{\Pi }_{1}x\left({\tau }_1\right)-{\Pi }_{2}y\left({\tau }_1\right)\in M_1,$ (18)

As $-d-w={\Pi }_1{h}_x\left(x^0,{\tau }_1\right)-{\Pi }_2{h}_y\left(y^0,{\tau }_1\right)$ . Further we have ${\Pi }_{1}x\left({\tau }_1\right)-{\Pi }_{2}y\left({\tau }_1\right)$ $\in M_1$ . From this [18] , we get that $\left(x\left({\tau }_1\right);y\left({\tau }_1\right)\right)\in M$ . The theorem is completely proved.

Proof of Theorem 2. In view of the triviality of the case ${\tau }_2=0$ we start with the case ${\tau }_2>0$ . We have (show (11), (12)) $-{\Pi }_1{h}_x\left(x^0,{\tau }_2\right)+{\Pi }_2{h}_y\left(y^0,{\tau }_2\right)$ $\in W_2\left({\tau }_2\right)$ . $W_2\left({\tau }_2\right)$ is an alternating integral with initial set $A_0=-M_1$ [8] [9] [10] . Therefore, it satisfies the semigroup property [9]

$\begin{array}{l}{W}_2\left({\tau }_2\right)\subset \left(W_2\left({\tau }_2-\epsilon \right)+{\displaystyle \underset{{\tau }_2-\epsilon }{\overset{{\tau }_2}{\int }}{\Pi }_1{r}^{\alpha -1}{E}_{\frac{1}{\alpha }}\left(A{r}^{\alpha };\alpha \right)P\text{d}r}\right)\\ \frac{*}{}{\displaystyle \underset{{\tau }_2-\epsilon }{\overset{{\tau }_2}{\int }}{\Pi }_2{r}^{\beta -1}{E}_{\frac{1}{\beta }}\left(B{r}^{\beta };\beta \right)Q\text{d}r},\end{array}$ (19)

where, $\epsilon$ ―arbitrary positive fixed number $0<\epsilon \le {\tau }_2$ ; ${\upsilon }_0\left(r\right)$ , ${\tau }_2-\epsilon \le r\le {\tau }_2$ ―an arbitrary measurable function with values in Q.

Let $\upsilon =\upsilon \left(t\right),0\le t<\infty$ ―arbitrary measurable function $\upsilon \left(t\right)\in Q$ . In accordance with the conditions of the theorem at time $t=0$ the narrowing becomes known $\upsilon \left(t\right),0\le t\le \epsilon$ , function $\upsilon \left(t\right),0\le t<\infty$ , on the line $\left[0,\epsilon \right]$ . It follows from the inclusion (19) that for an arbitrary function $\tilde{\upsilon }\left({\tau }_2-r\right),{\tau }_2-\epsilon \le r\le {\tau }_2$ , $\tilde{\upsilon }\left({\tau }_2-r\right)\in Q$ , we have

$\begin{array}{l}-{\Pi }_1{h}_x\left(x^0,{\tau }_2\right)+{\Pi }_2{h}_y\left(y^0,{\tau }_2\right)\in W_2\left({\tau }_2-\epsilon \right)\\ +{\displaystyle \underset{{\tau }_2-\epsilon }{\overset{{\tau }_2}{\int }}{\Pi }_1{r}^{\alpha -1}{E}_{\frac{1}{\alpha }}\left(A{r}^{\alpha };\alpha \right)P\text{d}r}\frac{*}{}{\displaystyle \underset{{\tau }_2-\epsilon }{\overset{{\tau }_2}{\int }}{\Pi }_2{r}^{\beta -1}{E}_{\frac{1}{\beta }}\left(B{r}^{\beta };\beta \right)\tilde{\upsilon }\left({\tau }_2-r\right)\text{d}r},\end{array}$ (20)

Thus, for an arbitrary function $\tilde{\upsilon }\left(s\right),0\le s\le \epsilon$ , there is an inclusion (20). Consequently, when $\tilde{\upsilon }\left(s\right)\equiv \upsilon \left(s\right),0\le s\le \epsilon$ , the inclusion (17). This implies the existence of a measurable function $u\left(s\right),0\le s\le \epsilon$ , such that 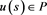and

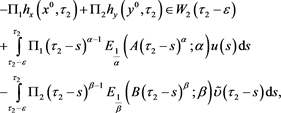(21)

than

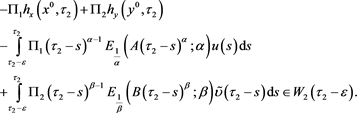(22)

We argue further in the same way as (21), (22). As

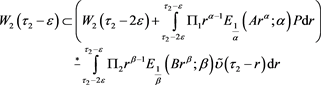(23)

we get

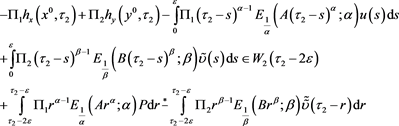(24)

for an (23), (24) arbitrary measurable function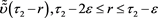,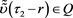. Consequently, there exists a measurable function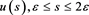, such that 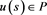and n

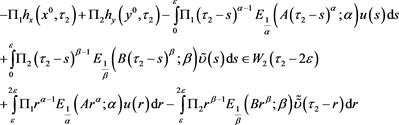(25)

It follows from (25) that

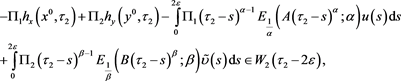(26)

etc. It is clear that there exists a natural number j such that: 1)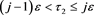; 2) by a known function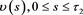, where 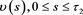narrowing of the function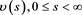, on the line, there exists a measurable function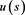, , 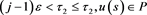satisfying the condition

(27)

and

(28)

therefore (26)-(28).

(29)

Similarly, by formulas (27)-(29) we eventually obtain

(30)

Thus (30), for a point we have, those. Trajectory, at the time is on the set M. The theorem is completely proved.

Proof of Theorem 3. By the hypothesis of Theorem (14), we have. Hence (13), there exists a measurable function, , when

(31)

Let an arbitrary measurable function (31), by the definition of the subtraction operation and from (7)-(9) we get

(32)

From this (32), in view of the measurability condition, there follows the existence of measurable functions, defined on a line and

(33)

A measurable function we define it as a solution of equation (33). Then for the solutions, relevant functions, we have

(34)

From (34) here, , those. Trajectory, at the time is on the set M. The theorem is completely proved.

5. Applying the Results to Specific Prosecution Processes

Example 1. Let the pursuer’s motion be described by equation

(35)

where―ratio of the length of the circle to its diameter. Movement of the evader is determined by the equation

(36)

where―limit value. The fractional derivative will be understood in the sense of Caputo. Phase vectors x and y determine

the current position in pursuer and escaping respectively. It is assumed that is four times, and―thrice continuously differentiable on function of time t, those,. Control vectors, are measurable functions of time t. Terminal set M has the form, where―linear subspace of the space,―subset,―orthogonal complement to the subspace в. Let,―single ball of. In our example―orthogonal projection operator from on. The game is considered to be over if conditions, those.

Because the A and B represent zero matrix, then and. The initial conditions for (35), (36) can be written in the form

(37)

and

(38)

Respectively (37), (38). We denote by

(39)

Now calculate the set, ,. By the conditions (39) of the problems, we have

(40)

Thus (40), the set there is a ball of radius, but many there is a ball of radius, and the geometric difference of these sets there is a ball of radius

(41)

The set defined by formula (9), (41) there is a ball of radius

(42)

It is (42) easy to prove that in order for the quantities, were positive for all, it suffices that the following inequalities hold

(43)

It is (43) clear that under these conditions all the conditions of the theorem are satisfied for this example 1. Thus, the quantity is the smallest positive root of the following equation

(44)

Example 2. Let in the Euclidean space dimension there are two points:―pursuing the motion, which is described by equation

(45)

and―the motion is given by the equation

(46)

where. The fractional derivative will be understood in the sense of Caputo. Phase vectors x and y determine the current position in pursuer and escaping respectively. It is assumed that is three times, and―twice continuously differentiable on function of time t, those.,

. Control vectors, are measurable functions of time t. A and B represent zero matrix, then and . The initial conditions for (44)-(46) can be written in the form

(47)

and respectively. We (47) denote by

(48)

The game is (48) considered to be over if conditions. Reasoning exactly the same in Example 1, we see that for this example all the conditions of Theorem 2 are satisfied. Then the equation for finding the end time of the game has the form

(49)

6. Conclusions

Summarizing the results obtained, we come to the conclusion that the differential game of pursuit of fractional order (1)-(3) starting at the moment t = 0 from the initial position, can be completed in a time not exceeding. Thus, sufficient conditions for solving similar problems are obtained in Theorems 1-3. The results obtained are applied to specific prosecution processes (49).

The research carried out to solve fractional differential games clearly demonstrates that fractional calculus is, in general, a more general and complex field of research than the classical differential games. Similarly, the theory of fractional dynamical systems and fractional calculus of variations include systems of integer order as special cases. The development of fractional differential games is just beginning, and therefore in this area there remains an extensive field for research. In particular, there is still no single clear interpretation of the geometric and physical meaning of fractional operators. There is also no single definition of the fractional derivative: in more abstract mathematical studies, as a rule, the Riemann-Lowville definition is used, and in more applied studies related to physics or control theory, in most cases the definition of Caputo is used or the definition of Grunwald-Letnikova. At the same time, the question of constructing standardizing functions for initial, boundary and initial boundary value problems that allow one to change the form of the in homogeneity in equations and thereby reduce the corresponding problems to problems with zero boundary or initial conditions becomes urgent.

Cite this paper

Mamatov, M. and Alimov, K. (2018) Differential Games of Persecution of Frozen Order with Separate Dynamics. Journal of Applied Mathematics and Physics, 6, 475-487. https://doi.org/10.4236/jamp.2018.63044

References