Journal of Applied Mathematics and Physics
Vol.04 No.11(2016), Article ID:71974,20 pages
10.4236/jamp.2016.411201
Numerical Solutions of Three-Dimensional Coupled Burgers’ Equations by Using Some Numerical Methods
Fatheah Ahmad Alhendi1, Aisha Abdullah Alderremy2
1Department of Mathematics, King Abdulaziz University, Jeddah, Kingdom of Saudi Arabia
2Department of Mathematics, King Khaild University, Abha, Kingdom of Saudi Arabia

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 6, 2016; Accepted: November 11, 2016; Published: November 14, 2016
ABSTRACT
In this paper, we found the numerical solution of three-dimensional coupled Burgers’ Equations by using more efficient methods: Laplace Adomian decomposition method, Laplace transform homotopy perturbation method, variational iteration method, variational iteration decomposition method and variational iteration homotopy perturbation method. Example is examined to validate the efficiency and accuracy of these methods and they reduce the size of computation without the restrictive assumption to handle nonlinear terms and it gives the solutions rapidly.
Keywords:
Three-Dimensional Coupled Burgers’ Equations, Laplace Transform, Adomian Decomposition, Homotopy Perturbation, Variational Iteration Method

1. Introduction
The Burgers Equation was first presented by Bateman [1] and treated later by J. M. Burgers (1895-1981) then it is widely named as Burgers’ Equation [2] . Burgers’ Equation is nonlinear partial differential equation of second order which is used in various fields of physical phenomena such as boundary layer behaviour, shock weave formation, turbulence, the weather problem, mass transport, traffic flow and acoustic transmission [3] [4] . In addition, coupled Burgers’ Equations has played an important role in many physical applications such as hydrodynamic turblence, vorticity transport, skock wave, dispersion in porous media and wave processes. In particular, the three-dimentional coupled Burgers’ Equations are important in large scale structure formation in the universe [5] [6] . In order to make a great application for burgers’ Equations, many researchers have been interested in solving it by various techniques. Analytic solution of one-dimensional Burgers’ Equation is got by many standard methods such as Backland transformation method, differential transformation method and tanh-coth method [6] , while an analytical solution of two-dimensional coupled Burgers’ Equations is first presented by Fletcher using the Hopf-Cole transformation [7] and an analytical solution of three-dimensional coupled Burgers’ Equations is derived by Srivastava et al using the variable of separable and Hopf-Cole transformation [6] . The finite difference, finite element, spectral methods, Adomian decomposition method, the variational iteration method, homotopy perturbation method HPM and Eulerian-Lagrangian method, etc. gave an numerical solution of one- and two-dimentional Burgers’ Equations [3] [8] - [15] .
Shukla et al are proposed a numerical solutions of three-dimensional coupled viscous Burgers’ Equations by using a modified cubic B-spline differential quadrature method [5] .
The motive of this paper is to find the numerical solution of three-dimensional coupled Burgers’ Equations by using more efficiently methods: Laplace Adomian decomposition method, Laplace transform homotopy perturbation method, the variational iteration method, variational iteration decomposition method and variational iteration homotopy perturbation method. We consider three-dimensional couple Burgers’ Equations as the following [6] :
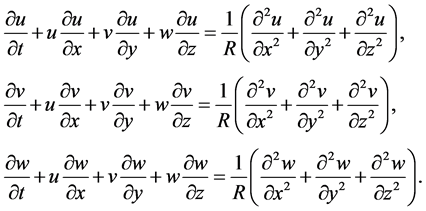 (1)
(1)
with the initial conditions:
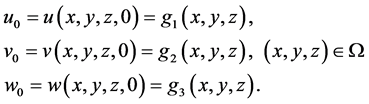 (2)
(2)
and the boundary conditions:
 (3)
(3)
where 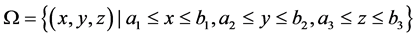 and
and 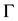 is its boundary,
is its boundary, 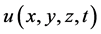 and
and 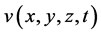 are the velocity components to be determined, g1, g2, g3, f1, f2 and f3 are known functions and R is the Reynolds number.
are the velocity components to be determined, g1, g2, g3, f1, f2 and f3 are known functions and R is the Reynolds number.
This paper is organized into five sections. Each method is in one section. We showed an overview of these methods then explained methodology and finally illustrated the methods by using examples. It is clear to see that numerical methods are reasonably in good covenant with the exact solution.
2. Laplace Adomian Decomposition Method
The Laplace transform LT is an integral transform discovered by Pierre-Simon Laplace. LT is a very powerful technique for solving ordinary and partial differential Equations, which transforms the original differential equation into an elementary algebraic expression [16] .
Definition: the Laplace transform of 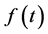 where
where , denoted by
, denoted by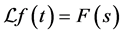 , is given by:
, is given by:
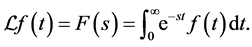
Adomian decomposition method ADM is proposed in 1980 by Grorge Adomian. ADM has been encountered much attention in recent years in applied mathematics in general and in solving Burgers’ Equations in particular. A wide class of linear and nonlinear, ordinary and partial differential Equations solved easily and more accurately via ADM. It has successfully used to handle most type of physical models of partial differential Equations without dependence on linearization or any restrictive assumptions that may change physical behavior of the models under study [3] [17] [18] [19] .
ADM consists of decomposing the unknown functions of any equations into a sums of an infinite number of components defined by the decomposition series:
 (4)
(4)
where  are to be determined in recursive manner. The nonlinear term
are to be determined in recursive manner. The nonlinear term 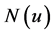 can be expressed by an infinite series of Adomian polynomial
can be expressed by an infinite series of Adomian polynomial 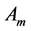 which is given as:
which is given as:
 (5)
(5)
where Adomian polynomial 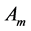 using the form
using the form
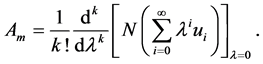 (6)
(6)
There is a growing interest of researchers has been to study the Adomian decomposition method ADM [3] [20] [21] [22] [23] . In this work, we will use Laplace transform- Adomian decomposition method (LT-ADM) introduced by Khuri khuri [24] . Some time it is known as Laplace Adomian decomposition method (LADM). This numerical technique explains how the Laplace transform may be used to approximate the solutions of the nonlinear partial differential equations (PDEs) including Burgers’ Equations with the decomposition method [11] [24] [25] [26] .
2.1. Methodology of LT-ADM for Three-Dimensional Couple Burgers’ Equations
We consider the system (1) and apply LT on both side of it:

We can write (7) as:

By using (2) we get:

Using inverse Laplace transform on both sides of (9), we have

from (4) we can write the solutions as:

Now, we assume the nonlinear terms as:

where 


where

2.2. Example
Consider (1) if the exact solution is [5] :

To solve this example by LT-ADM, we follow the methodology which discussed in subsection (2.1). The accuracy of LT-ADM for the three-dimensional coupled Burgers’ Equations agrees very well with the exact solution and absolute errors are very small for the current choice of x, y, z and t. The results are shown in Tables 1-3 for R = 100, x = 0.1, y = 0.02 and z = 0.03.
3. Laplace Transform Homotopy Perturbation Method
Homotopy perturbation method HPM was first proposed by He. HPM is combination of traditional perturbation method and homotopy method. The important advantage of HPM is that the nonlinear term can be easily handled. It is easy to calculate the solution
Table 1. The absolute error (AEs) of 
Table 2. The AEs of 
Table 3. The AEs of 
with this method. Linear or nonlinear ODEs and PDEs are studied successfully by using LT-HPM [17] , [27] [28] [29] [30] [31] . To figure out how HPM works [32] , consider n-dimensional Burgers’ equation

We construct the following homotopy:

or

where



parameter while 

Now, substituting 

The solution is

In [33] , Aminikhah presented LT-HPM to solve nonlinear Blasius' viscous flow equation. In [34] , some application examples of LT-HPM for nonlinear ODEs with Dirichlet, mixed, and Neumann boundary conditions were presented. It has used to solve PDEs then to solve Burgers’ Equations [12] [14] [30] [31] [34] .
Now, we are going to study LT-HPM for (1) as following.
3.1. Methodology of LT-HPM for Three-Dimensional Couple Burgers’ Equations
We consider the system (1) and apply HPM on it. We construct the following homo- topy:

where 




we can write (22) as:

Applying LT on both side of (24)

By applying inverse of LT on (25), we get

By substituting U, V and W from (23) in (26) and comparing coefficients of terms with identical powers of p:

Finally, the approximate solutions are:

3.2. Example
To solve (1) by LT-HPM, we follow the methodology which discussed in subsection (3.1). The results in Tables 4-6 show that LT-HPM is more effective and high accuracy when compared with the exact solutions for R = 100, x = 0.1, y = 0.02 and z = 0.03.
Table 4. The AEs of 
Table 5. The AEs of 
Table 6. The AEs of 
4. The Variational Iteration Method
The variational iteration method (VIM) was proposed by Ji-Huan He in 1997 [35] [36] [37] [38] . The VIM has been applied successfully for the most important problems in physically important phenomena including Burgers’ Equation [13] [39] [40] [41] [42] The VIM solve linear or nonlinear ODEs and PDEs without needing small parameter or linearization and by few iterations lead to high accurate solutions.
To explain the basic concepts of the VIM, we consider n-dim of burgers’ Equation (16). We can write the correction functional for it as [32] :

where





4.1. Methodology of VIM for Three-Dimensional Couple Burgers’ Equations
Consider the system (1), we can construct a the following correction functional:



4.2. Example
To solve (1) by VIM, we follow the methodology which discussed in subsection (4.1). The results in Tables 7-9 are shown that the efficiency and accuracy of the VIM. It reduces the size of computation without the restrictive assumption to handle nonlinear terms and it gives the solutions rapidly.
5. Variational Iteration Decomposition Method
The variational iteration decomposition method (VIDM) is technique combination of two the most powerful mathematical methods for solving a large class of differential Equations, namely variational iteration method and Adomian decomposition method. In 2007 VIDM has been used to solve quadratic Riccati differential Equation problems
Table 7. The AEs of 
Table 8. The AEs of 
Table 9. The AEs of 
[43] . Noor et al. [44] [45] used this method for solving eighth-order boundary value problems, sixth-order boundary value problems and higher dimensional initial boundary value problems. Grover and Tomer solved twelfth order boundary value problems by using VIDM. In 2013, the fractional Riccati differential Equation is solved by VIM by using Adomian polynomials for nonlinear terms [46] .
To illustrate the general concept of VIDM by using (5), (6) in (29), hence, we have the correction functional for (16) as:

We are solved three-dimensional coupled Burgers’ Equations by using VIDM as following.
5.1. Methodology of VIDM for Three-Dimensional Couple Burgers’ Equations
We consider the system (1). Next, by using (11) and (12) in (32), we obtain the iterative scheme to find the approximate solutions by VIDM as following:

5.2. Example
To solve (1) by VIDM by using (34). The numerical results in Tables 10-12 show that VIDM is an effective and powerful method to find better results.
Table 10. The AEs of 
Table 11. The AEs of 
Table 12. The AEs of 
6. Variational Iteration Homotopy Perturbation Method
The variational iteration homotopy perturbation method (VIHPM) is combination of two well-known methods, namely variational iteration method and homotopy perturbation method. VIHPM has been applied in [32] [47] - [52] for solving a large class of differential Equations.
To illustrate the concept of VIHPM [32] , we consider (16) and assume the solution of (16) has the form

from (35), (16) can be written as:

we can from the correction functional for(36) we can write

where


The approximate solutions are give by

we used this method to solve three-dimensional coupled Burgers’ Equations as fol- lowed.
6.1. Methodology of VIHPM for Three-Dimensional Couple Burgers’ Equations
we consider the correction functional (31) with 

by VIHPM, we have


by comparing the coefficients of like power of p, we get

The approximate solutions are given by

6.2. Example
To solve (1) by VIHPM, we follow the methodology discussed in subsection (6.1). The accuracy of VIHPM for the three-dimensional coupled Burgers’ Equations agrees very well with the exact solution and absolute errors are very small for the current choice of x, y, z and t. The result are shown in Tables 13-15 for R = 100, x = 0.1, y = 0.02 and z = 0.03.
7. Conclusion
In this work, these previous methods mentioned above have been successfully used for finding the solution of three-dimensional coupled Burgers’ Equations. The numerical
Table 13. The AEs of 
Table 14. The AEs of 
Table 15. The AEs of 
results are obtained for approximation and compared with the exact solutions and the results show that we achieve an excellent approximation to the actual solution of the equations by using only two iterations. The results show that these methods are powerful mathematical tools to solving a three-dimensional coupled Burgers’ Equation. In our work, we use the Maple to calculate approximate solutions in our systems by using those very efficient methods.
Acknowledgements
This paper was funded by King Abdulaziz City for Science and Technology (KACST) in Saudi Arabia. The authors therefore thank them for their full collaboration.
Cite this paper
Alhendi, F.A. and Alderremy, A.A. (2016) Numerical Solutions of Three-Dimensional Coupled Burgers’ Equations by Using Some Numerical Methods. Journal of Applied Mathematics and Physics, 4, 2011-2030. http://dx.doi.org/10.4236/jamp.2016.411201
References
- 1. Bateman, H. (1915) Some Recent Researches on the Motion of Fluids. Monthly Weather Review, 43, 163-170.
http://dx.doi.org/10.1175/1520-0493(1915)43<163:SRROTM>2.0.CO;2 - 2. Burgers, J.M. (1948) A Mathematical Model Illustrating the Theory of Turbulence. Advances in Applied Mechanics, 1, 171-199.
http://dx.doi.org/10.1016/S0065-2156(08)70100-5 - 3. Wazwaz, A.M. (2002) Partial Differential Equations: Methods and Applications. Balkema, Cape Town.
- 4. Naghipour, A. and Manafian, J. (2015) Application of the Laplace Adomian Decomposition and Implicit Methods for Solving Burgers’ Equation. TWMS Journal of Pure and Applied Mathematics, 6, 68-77.
- 5. Shukla, H.S., Tamsir, M., Srivastava, V.K. and Rashidi, M.M. (2016) Modified Cubic β-Spline Differential Quadrature Method for Numerical Solution of Three-Dimensional Coupled Viscous Burger Equation. Modern Physics Letters B, 30, Article ID: 1650110.
http://dx.doi.org/10.1142/s0217984916501104 - 6. Srivastava, V.K. and Ashutosh, M.T. (2013) Generating Exact Solution of Three-Dimensional Coupled Unsteady Nonlinear Generalized Viscous Burgers’ Equations. International Journal of Mathematical Sciences, 5, 1-13.
- 7. Fletcher, C.A. (1983) Generating Exact Solutions of the Two-Dimensional Burgers’ Equations. International Journal for Numerical Methods in Fluids, 3, 213-216.
http://dx.doi.org/10.1002/fld.1650030302 - 8. Fletcher, C.A.J. (1983) A Comparison of Finite Element and Finite Difference Solutions of the One-and Two-Dimensional Burgers’ Equations. Journal of Computational Physics, 51, 159-188.
http://dx.doi.org/10.1016/0021-9991(83)90085-2 - 9. Kutluay, S., Bahadir, A.R. and Ozdes, A. (1999) Numerical Solution of One-Dimensional Burgers Equation: Explicit and Exact-Explicit Finite Difference Methods. Journal of Computational and Applied Mathematics, 103, 251-261.
http://dx.doi.org/10.1016/S0377-0427(98)00261-1 - 10. Mittal, R.C. and Sighal, P. (1996) Numerical Solution of Periodic Burgers Equation. Indian Journal of Pure and Applied Mathematics, 27, 689-700.
- 11. Khan, M. (2014) A Novel Solution Technique for Two Dimensional Burger’s Equation. Alexandria Engineering Journal, 53, 485-490.
http://dx.doi.org/10.1016/j.aej.2014.01.004 - 12. Ahmad, J., Bibi, Z. and Noor, K. (2014) Laplace Decomposition Method Using He’s Polynomial to Burgers Equation. Journal of Science and Arts, 14, 131-138.
- 13. Abdou, M.A. and Soliman, A.A. (2005) Variational Iteration Method for Solving Burger’s and Coupled Burger’s Equations. Journal of Computational and Applied Mathematics, 181, 245-251.
http://dx.doi.org/10.1016/j.cam.2004.11.032 - 14. Desai, K.R. and Pradhan, V.H. (2012) Solution of Burger’s Equation and Coupled Burger’s Equations by Homotopy Perturbation Method. International Journal of Engineering Research and Applications, 2, 2033-2040.
- 15. Young, D.L., Fan, C.M., Hu, S.P. and Atluri, S.N. (2008) The Eulerian-Lagrangian Method of Fundamental Solutions for Two-Dimensional Unsteady Burgers’ Equations. Engineering Analysis with Boundary Elements, 32, 395-412.
http://dx.doi.org/10.1016/j.enganabound.2007.08.011 - 16. Schiff, J.L. (1999) The Laplace Transform: Theory and Applications. Springer, Berlin.
http://dx.doi.org/10.1007/978-0-387-22757-3 - 17. Adomian, G. (1986) Nonlinear Stochastic Operator Equations. Academic Press, Pittsburgh.
- 18. Adomian, G. (1988) A Review of the Decomposition Method in Applied Mathematics. Journal of Mathematical Analysis and Applications, 135, 501-544.
http://dx.doi.org/10.1016/0022-247X(88)90170-9 - 19. Adomian, G. (1996) Solution of Coupled Nonlinear Partial Differential Equations by Decomposition. Computers Mathematics with Applications, 31, 117-120.
http://dx.doi.org/10.1016/0898-1221(96)00010-7 - 20. Bougoffa, L., Rach, R., Wazwaz, A. and Duan, J.-S. (2015) On the Adomian Decomposition Method for Solving the Stefan Problem. International Journal of Numerical Methods for Heat & Fluid Flow, 25, 912-928.
http://dx.doi.org/10.1108/HFF-05-2014-0159 - 21. El-Borai, M.M., El-Sayed, W.G. and Jawad, A.M. (2015) Adomian Decomposition Method for Solving Fractional Differential Equations. International Research Journal of Engineering and Technology, 2, 296-306.
- 22. Pourgholi, R. and Saeedi, A. (2015) A Numerical Method Based on the Adomian Decomposition Method for Identifying an Unknown Source in Non-Local Initial-Boundary Value Problems. International Journal of Mathematical Modelling and Numerical Optimisation, 6, 185-197.
http://dx.doi.org/10.1504/IJMMNO.2015.071869 - 23. Alkresheh, H.A. and Ismail, A.M. (2016) An Algorithm for Positive Solution of Boundary Value Problems of Nonlinear Fractional Differential Equations by Adomian Decomposition Method. Journal of Interpolation and Approximation in Scientific Computing, 2016, 25-37.
http://dx.doi.org/10.5899/2016/jiasc-00090 - 24. Khuri, S.A. (2001) A Laplace Decomposition Algorithm Applied to a Class of Nonlinear Differential Equations. Journal of Applied Mathematics, 1, 141-155.
http://dx.doi.org/10.1155/S1110757X01000183 - 25. Zafar, Z.U. and Ahmed, M.O. (2013) Solution of Burger’s Equation with the Help of Laplace Decomposition Method. Pakistan Journal of Engineering and Applied Sciences, 12, 39-42.
- 26. Fadaei, J. (2011) Application of Laplace-Adomian Decomposition Method on Linear and Nonlinear System of Pdes. Applied Mathematical Sciences, 5, 1307-1315.
- 27. He, J.H. (1999) Homotopy Perturbation Technique. Computer Methods in Applied Mechanics and Engineering, 178, 257-262.
http://dx.doi.org/10.1016/S0045-7825(99)00018-3 - 28. He, J.H. (2000) A Coupling Method of a Homotopy Technique and a Perturbation Technique for Non-Linear Problems. International Journal of Non-Linear Mechanics, 35, 37-43.
http://dx.doi.org/10.1016/S0020-7462(98)00085-7 - 29. He, J.H. (2003) Homotopy Perturbation Method: A New Nonlinear Analytical Technique. Applied Mathematics and Computation, 135, 73-79.
http://dx.doi.org/10.1016/S0096-3003(01)00312-5 - 30. Liao, S. (2012) Homotopy Analysis Method in Nonlinear Differential Equations. Springer, Berlin.
http://dx.doi.org/10.1007/978-3-642-25132-0 - 31. Srivastava, V.K. and Awasthi, M.K. (2014) (1 + n)-Dimensional Burgers’ Equation and Its Analytical Solution: A Comparative Study of Hpm, Adm and Dtm. Ain Shams Engineering Journal, 5, 533-541.
http://dx.doi.org/10.1016/j.asej.2013.10.004 - 32. Hendi, F.A., Kashkari, B.S. and Alderremy, A.A. (2016) The Variational Homotopy Perturbation Method for Solving Dimensional Burgers’ Equations. Journal of Applied Mathematics, 2016, Article ID: 4146323.
http://dx.doi.org/10.1155/2016/4146323 - 33. Aminikhah, H. (2012) Analytical Approximation to the Solution of Nonlinear Blasius’ Viscous Flow Equation by Ltnhpm. ISRN Mathematical Analysis, 2012, Article ID: 957473.
http://dx.doi.org/10.5402/2012/957473 - 34. Filobello-Nino, U., Vazquez-Leal, H., Khan, Y., Perez-Sesma, A., Diaz-Sanchez, A., Jimenez-Fernandez, V.M., Herrera-May, A., Pereyra-Diaz, D., Mendez-Perez, J.M. and Sanchez-Orea, J. (2013) Laplace Transform-Homotopy Perturbation Method as a Powerful Tool to Solve Nonlinear Problems with Boundary Conditions Defined on Finite Intervals. Computational and Applied Mathematics, 34, 1-16.
http://dx.doi.org/10.1007/s40314-013-0073-z - 35. He, J.H. (1997) A New Approach to Nonlinear Partial Differential Equations. Communications in Nonlinear Science and Numerical Simulation, 2, 230-235.
http://dx.doi.org/10.1016/S1007-5704(97)90007-1 - 36. He, J.H. (1998) A Variational Iteration Approach to Nonlinear Problems and Its Applications. Mechanical Application, 20, 30-31.
- 37. He, J.H. (1999) Variational Iteration Method—A Kind of Non-Linear Analytical Tech-nique: Some Examples. International Journal of Non-Linear Mechanics, 34, 699-708.
http://dx.doi.org/10.1016/S0020-7462(98)00048-1 - 38. He, J.H. (2007) Variational Iteration Method-Some Recent Results and New Interpretations. Journal of Computational and Applied Mathematics, 207, 3-17.
http://dx.doi.org/10.1016/j.cam.2006.07.009 - 39. Wazwaz, A.M. (2007) The Variational Iteration Method for Solving Linear and Nonlinear Systems of Pdes. Computers & Mathematics with Applications, 54, 895-902.
http://dx.doi.org/10.1016/j.camwa.2006.12.059 - 40. Wazwaz, A.M. (2007) A Comparison between the Variational Iteration Method and Adomian Decomposition Method. Journal of Computational and Applied Mathematics, 207, 129-136. http://dx.doi.org/10.1016/j.cam.2006.07.018
- 41. Biazar, J. and Aminikhah, H. (2009) Exact and Numerical Solutions for Non-Linear Burger’s Equation by Vim. Mathematical and Computer Modelling, 49, 1394-1400.
http://dx.doi.org/10.1016/j.mcm.2008.12.006 - 42. Batiha, B. (2012) Varational Itrational Method and Its Applications. Lap Lambert Academic Publishing GmbH & Co. KG, Germany.
- 43. Abbasbandy, S. (2007) A New Application of He’s Variational Iteration Method for Quadratic Riccati Differential Equation by Using Adomian’s Polynomials. Journal of Computational and Applied Mathematics, 207, 59-63.
http://dx.doi.org/10.1016/j.cam.2006.07.012 - 44. Noor, M.A. and Mohyud-Din, S.T. (2008) Variational Iteration Decomposition Method for Solving Eighth-Order Boundary Value Problems. International Journal of Differential Equations, 2007, Article ID: 19529.
- 45. Noor, M.A., Noor, K.I. and Mohyud-Din, S.T. (2009) Variational Iteration Method for Solving Sixth-Order Boundary Value Problems. Communications in Nonlinear Science and Numerical Simulation, 14, 2571-2580.
http://dx.doi.org/10.1016/j.cnsns.2008.10.013 - 46. Jafari, H., Tajadodi, H. and Baleanu, D. (2013) A Modified Variational Iteration Method for Solving Fractional Riccati Differential Equation by Adomian Polynomials. Fractional Calculus and Applied Analysis, 16, 109-122.
http://dx.doi.org/10.2478/s13540-013-0008-9 - 47. Matinfar, M., Mahdavi, M. and Raeisy, Z. (2010) The Implementation of Variational Homotopy Perturbation Method for Fisher’s Equation. International Journal of Nonlinear Science, 9, 188-194.
- 48. Liu, Y. (2012) Variational Homotopy Perturbation Method for Solving Fractional Initial Boundary Value Problems. Abstract and Applied Analysis, 2012, Article ID: 727031.
http://dx.doi.org/10.1155/2012/727031 - 49. Allahviranloo, T., Armand, A. and Pirmohammadi, S. (2014) Variational Homotopy Perturbation Method: An Efficient Scheme for Solving Partial Differential Equations in Fluid Mechanics. The Journal of Mathematics and Computer Science, 9, 362-369.
- 50. Daga, A. and Pradhan, V. (2014) A Novel Approach for Solving Burger’s Equation. Applications & Applied Mathematics, 9, 541-552.
- 51. Mahdy, A.M.S., Mohamed, A.S. and Mtawa, A.A.H. (2015) Variational Homotopy Perturbation Method for Solving the Generalized Time-Space Fractional Schrdinger Equation. International Journal of Physical Sciences, 10, 342-350.
http://dx.doi.org/10.5897/IJPS2015.4287 - 52. Easif, F.H., Manaa, S.A., Mahmood, B.A. and Yousif, M.A. (2015) Variational Homotopy Perturbation Method for Solving Benjamin-Bona-Mahony Equation. Applied Mathematics, 6, 675-683.
http://dx.doi.org/10.4236/am.2015.64062


