Journal of Applied Mathematics and Physics
Vol.04 No.09(2016), Article ID:70897,25 pages
10.4236/jamp.2016.49181
Planar Retro-Reflector for Grazing Incident Beam of High-Energy X-Ray Photons*
Hakob Jacob Bezirganyan1,2#, Robert Bezirganyan1,3, Siranush Bezirganyan1,4
1X-Ray Optical Memory, Inc., Bellevue, WA, USA
2V Group Inc., Cranbury, NJ, USA
3University of Washington, Bothell, WA, USA
4Bellevue College, Main Campus, Bellevue, WA, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 17, 2016; Accepted: September 24, 2016; Published: September 27, 2016
ABSTRACT
The grazing-incidence hard X-ray retro-reflector (GIRR) is a novel optical element, which completely suppresses the conventional mirror beam in the retro-reflection mode, and, at the same time, totally reflects the primary grazing incident X-radiation backwards to its source in strictly anti-parallel direction with minimal scattering. The GIRR is a good alternative to hard X-ray normal-incidence Bragg mirror, and has a high potential for applications in various X-ray optical devices and techniques, such as, hard X-ray optical noise (or background) filters, high-quality hard X-ray waveguides, low-gain hard X-ray free electron laser resonators (XFELRs), X-ray holography, coherent X-ray diffraction imaging, phase-contrast imaging, as well as in hard X-ray optical data storage devices and deep space hard X-ray communications. The proposed optical element consists of single-crystal wafer covered by a thin, non-diff- racting layer of low-absorbing material.
Keywords:
X-Ray, Diffraction Theory, Single-Crystal, Total Retro-Reflection, Mathieu Functions

1. Introduction
The development of high quality hard X-ray retro-reflectors is important, since the later they can be used in solving of various challenges facing modern advanced hard X-ray optical engineering.
During the last two decades, there has been an essential progress in the design, modelling, fabrication and applications of optical retro-reflectors [1] - [5] , especially, in the sphere of the evolving technology and applications in optical wireless communications (OWC) from short to long distances [6] - [9] .
However, the direct extension for existing technologies from optical region to shorter X-ray wavelengths is not possible. The retro-reflection techniques developed for visible light don’t work for hard X-ray wavelengths because the refractive index of X-rays is slightly less than the unity for most substances. A common way to overcome this problem is through the application of various X-ray diffraction methods [10] - [13] .
Consider the well-known technique of normal-incidence hard X-ray Bragg reflection [14] - [18] which is utilized in, for example, simple two-crystal plate cavity [19] - [24] , as well as in multi-cavity [25] [26] Fabry-Perot (FP) resonators when the magnitude of Bragg angle 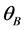 is close to 90˚. The cavities are separated by the crystal plates with specific thickness ratios and, basically, have a common monolithic crystal base. These plates act as a normal-incidence backward reflecting Bragg mirrors. However, such resonators require a stringent temperature control, since the crystal plates themselves are affected by thermal expansion, which, in its turn, leads to a problem of non-stability in lattice parameter of the diffracting planes
is close to 90˚. The cavities are separated by the crystal plates with specific thickness ratios and, basically, have a common monolithic crystal base. These plates act as a normal-incidence backward reflecting Bragg mirrors. However, such resonators require a stringent temperature control, since the crystal plates themselves are affected by thermal expansion, which, in its turn, leads to a problem of non-stability in lattice parameter of the diffracting planes . The overall uncertainty in modern measurements of, for example, the Si lattice parameter is
. The overall uncertainty in modern measurements of, for example, the Si lattice parameter is 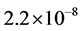 and thermal expansion at 22.5˚C is
and thermal expansion at 22.5˚C is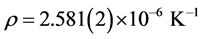 . Therefore, it is desirable to know the crystal temperature well enough, and have it controlled precise enough, to keep the Si lattice constant
. Therefore, it is desirable to know the crystal temperature well enough, and have it controlled precise enough, to keep the Si lattice constant 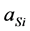 unchanged within
unchanged within  accuracy. According to above conditions, the temperature accuracy
accuracy. According to above conditions, the temperature accuracy 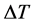 should not exceed the following value of
should not exceed the following value of 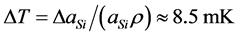 [27] - [29] .
[27] - [29] .
The absorption, and, consequently, the crystal plate heating problem are partially solved in [23] , where, instead of a conventional cavity with normal incidence, the authors of paper [23] use an inclined incident beam along one of the multiple diffraction directions to generate back diffraction in a resonator cavity. To address to change in the angle of incidence, authors remove the absorption in the first crystal, in contradiction to conventional normal-incidence one-cavity FR resonators setup.
2. Total Retro-Reflection of Grazing Incident X-Rays
In this paper, the authors propose and investigate the grazing-incidence hard X-ray backward reflector or retro-reflector (GIRR), which totally reflects the primary grazing incident X-radiation backwards to its source in strictly anti-parallel direction with minimal scattering.
The authors overcome the retro-reflector’s thermal expansion problem by using the X-ray grazing-incidence diffraction scheme, based on the fact that the X-ray penetration depths in a crystal are at least in three orders smaller than in the case of a normal-incidence Bragg mirror. The equations and corresponding graphs of the depths of penetration of hard X-rays in single-crystal are presented in [30] . Also, the energy distribution of the primary beam along the crystal entrance surface is, at least, two orders of magnitude smaller in the case of grazing-incidence diffraction than the energy distribution for the same primary beam in the case of normal-incidence Bragg reflectors. These two circumstances clearly satisfy the requirement of keeping the crystal temperature precisely at a predefined level.
2.1. Coplanar Grazing-Incidence X-Ray Backscattering Diffraction (GIXB)
First, let’s consider the following two reflection schemes from a variety of wave reflectivity models. The fist scheme is a conventional reflection scheme of the plane electromagnetic wave from planar mirror (see Figure 1). According to Figure 1, the equation  holds, where the angles
holds, where the angles 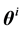 and
and  are the angles of incidence and reflectance, respectively. The wave vectors of incident
are the angles of incidence and reflectance, respectively. The wave vectors of incident 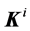 and reflected
and reflected 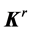 beams lie in this figure on the different sides of the normal line to the interface between two media. The vectors
beams lie in this figure on the different sides of the normal line to the interface between two media. The vectors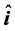 ,
, 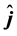 and
and 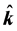 are unit vectors along positive directions of Ox-, Oy-, and Oz-axis, respectively.
are unit vectors along positive directions of Ox-, Oy-, and Oz-axis, respectively.
The second scheme is a retro-reflection scheme of the plane electromagnetic wave (see Figure 2). According to Figure 2, the equation 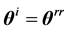 holds, where the angles
holds, where the angles 




One may note that the coplanar geometry of the grazing-incidence hard X-ray backscattering diffraction (GIXB, see the scheme in Figure 3 and translations [30] [31] of our original papers) contains both coplanar reflection schemes presented in Figure 1 and Figure 2. The GIXB technique is a dynamical Bragg diffraction, which holds under
Figure 1. A scheme of conventional reflection from planar mirror.
Figure 2. A scheme of grazing-incidence retro-reflection from planar mirror.
Figure 3. A scheme of coplanar grazing-incidence hard X-ray backscattering diffraction (GIXB) by the diffracting single-crystal wafer.



the conditions of total external reflection, and is extremely sensitive to variations of the spacing period 



The plane 
















where 






Equation (4b) is the exact condition for the particular case of coplanar GIXB setup derived from general GIXB equations [29] [30] . In this case, the angle of incidence, at which proposed planar mirror reflects X-rays in reverse way, is close to right angle, unlike the homogeneous planar optical mirror, which does this only if the mirror is exactly perpendicular to the wave front, having a zero angle of incidence. The vector 










where



2.2. Grazing-Incidence Hard X-Ray Retro-Reflector (GIRR)
Now, let’s clarify the performance criteria of the planar grazing-angle incidence hard X-ray retro-reflector (GIRR):
1) A grazing-incidence planar retro-reflector is a mirror with a plane surface that totally reflects (or diffracts) the electromagnetic wave back to its source, and, consequently, the conventional mirror wave is completely suppressed (that is the reflectivity coefficient of conventional mirror wave is equal to zero, see Figure 2).
2) The wave vectors of incident and retro-reflected (or backward diffracted) waves are strictly collinear (see Figure 2).
Therefore, all the types of non-coplanar grazing-incidence hard X-ray diffraction geometries (for example, see [32] ) are not applicable for the GIRR since they do not satisfy the requirement 2). Fortunately, it is possible to transform the coplanar GIXB scheme given in Figure 3 into the required GIRR scheme as given in Figure 2.
・ Thus, the main goal of presented theoretical research is the elaboration and estimation of certain physical and technical solutions that can help to completely suppress a conventional mirror wave 

We propose a solution to this problem through the coplanar GIXB that holds in a single-crystal wafer covered by an ultra-thin, non-diffracting layer of low-absorbing material (see Figure 4). The total retro-reflection can be achieved by ensuring that the
Figure 4. A scheme of coplanar grazing-incidence hard X-ray backscattering diffraction (GIXB) by the diffracting single-crystal wafer covered with an ultra-thin non-diffracting layer of low-absorbing material.



intensity of conventional mirror wave is reduced by destructive interference between the wave reflected from wafer and the wave reflected from cover layer. A scheme of proposed GIRR is presented in Figure 4, where the plane 


In a particular case of the specular beam suppression mode [32] [33] , the scheme of coplanar grazing-incidence X-ray backscattering diffraction (GIXB) presented in Figure 4 corresponds to total retro-reflection.
The mentioned above grazing-incidence retro-reflection from the proposed planar X-ray optical device is an X-ray analogue of the reflection phenomenon when a light beam is propagating in a photonic crystal, and is incident upon the plane interfaces between the crystal and a uniform dielectric [34] . The authors of paper [34] showed that neither the phase velocity nor the group velocity directions of reflected beam satisfies Snell’s law. The system exhibits remarkable and unusual reflection effects. In particular, total internal reflection is absent except at discrete angular values. The direction of the reflected beam can also be pinned along special crystal directions, independent of the orientation of the interface. At grazing incidences, strong backward reflection occurs (see figure 4 in [34] ). These effects may be important for creating integrated photonic circuits, and for on-chip image transfer [34] .
3. Stationary X-Ray Wave Fields in the Vacuum
All vacuum waves are traveling in the space region




where 






We seek a non-trivial y-component 




where 
4. Stationary X-Ray Wave Fields inside GIRR
The considered model of GIRR extends over the volume




where 









In general, dielectric permittivity








4.1. Solution of the Problem Using a Method of Finding the Eigenvalues and Eigenfunctions
The study of wave propagation in one-dimensional periodic media was pioneered by G. Floquet in 1883 [35] . This theory was extended for three-dimensional periodic media by F. Bloch in 1928 [36] . Bloch proved that waves in such a medium can propagate without scattering, their behaviour governed by a periodic envelope function multiplied by a plane wave.
The same technique can be applied to electromagnetism by considering Maxwell’s equations as an eigenvalues and eigenfuctions problem by analogue with Schrödinger’s equation (see [30] - [33] ). Using such approach, we treat the dynamical diffraction of X-rays by a set of diffracting lattice planes 

4.2. Stationary X-Ray Wave Fields inside Non-Diffracting Cover Layer
We seek a non-trivial y-component 



where








4.3. Stationary X-Ray Wave Fields inside the Single-Crystal Wafer
If absorption is not taken into account, and crystalline wafer has a center of symmetry, then the following relations describe components of the stationary X-ray wave fields 


where














5. Boundary Conditions and Extension of Results for the Absorbing Media
We do not make any assumptions about the X-ray wave field strengths






Using the orthogonality conditions of the functions involved in Equations (7b), (8b), (13b) and (15b), the unknown weight functions



In our calculation, the absorption is taken into account by the following substitutions made in the obtained results:



where


6. The Advanced Technologies That Can Be Used for Manufacturing of Hard X-Ray GIRRs
This paper further considers a total retro-reflection of grazing incident hard X-rays from a germanium wafer covered by a thin beryllium layer.
6.1. Choice of Germanium as a Diffracting Substrate for GIRR
The choice of germanium single-crystal wafer for use in GIRR is stipulated by the following reason:
・ Germanium has relatively low melting point and was the first material that could be grown dislocation free. With the improvement of crystal growth, dislocation-free wafers became available and are nowadays the standard in the case of 200 and 400 mm diameter germanium and silicon substrates [40] - [43] .
6.2. Selection of Beryllium as a Cover Layer Material for GIRR
The selection of beryllium as a base material for non-diffracting cover layer is stipulated by the following:
・ Beryllium is a metal that has low density and low atomic mass, and hence very low absorption level of X-rays, making beryllium the preferred choice for X-ray tube windows where the energy low absorption is desired.
・ The surface of beryllium metal, like the aluminum, is covered by a thin layer of oxide that helps protect the metal from attack by acids. Due to this coating, corrosion and oxidation in air is minimal up to temperatures of about 760˚C. Beryllium metal does not react with water or steam, even if the metal is heated to red heat.
6.3. A Technique for Deposition of Thin Metallic Layers on Semiconductors
The deposition of the beryllium thin layer can, for example, be realized via Atomic Layer Deposition (ALD) technology:
・ ALD technology allows semiconductor manufacturers to choose from a wide field of deposition precursors for the application of any thin film in use today on the surface of a large wafer with atomic layer precision.
・ ALD technology can also be used to construct complex, compound film structures with a level of control and conformity that was previously unavailable or impractical.
・ ALD offers the opportunity to create precisely controlled ultra-thin films coating up to 300 mm diameter single-crystal wafers.
・ General ALD process benefits are the excellent process control with wafer-to-wafer repeatability with accuracy less than ±1%, up to 300 mm diameter wafer with typical uniformity accuracy less than ±2%, excellent step coverage even inside high aspect ratio structures, low film impurities, etc. (for example, see [44] ).
6.4. The Thermal Annealing of GIRR
The improvement of tensile strain, crystal quality, and surface morphology of germanium wafer after its covering with thin beryllium layer can be achieved by the thermal annealing. For example, the tensile strain and crystal surface quality, of 500 nm thick Ge films were improved after rapid thermal annealing at 900˚C for a short period less than 20 s [45] . The films were grown on Si(001) substrates by ultra-high vacuum chemical vapour deposition. These improvements are attributed to relaxation and defect annihilation in the Ge films. However, after prolonged more than 20 s rapid thermal annealing, tensile strain and crystal quality degenerated. This phenomenon results from intensive Si-Ge mixing at high temperature.
The solid solubility of beryllium in germanium is extremely small up to temperatures of about 900˚C, and, consequently, the mutual diffusion process of atoms between germanium wafer and beryllium layer has very low rate (see Fig. 15.11 in [46] ).
・ This type of properties opens the opportunity of removing the interface tensile strain and improving the crystal quality and morphology of subsurface region of germanium wafer covered by thin beryllium layer through the application of a longer thermal annealing method at, for example, 700˚C practically without any appreciable inter-diffusion between these two materials. The essential reduction of the tensile strain along the Be-Ge large interface will increase the survivability of the coverage layer.
6.5. The Array of GIRRs
The main problem of experimental research involving the grazing-incidence hard X-ray optics is the small collection efficiency due to the small critical angle, since the collection area of grazing incidence mirrors is the projection of the mirror surface onto the aperture plane.
A Japanese optics company, JTEC Corporation, fabricates the mirrors for synchrotrons and other X-ray laser research facilities [47] such as Japan’s Spring-8 Angstrom Compact Free-Electron Laser (SACLA) and the European X-ray Free-Electron Laser (EXFEL), located in Hamburg, Germany and due to come online in 2017. Recently, scientists installed new mirrors to improve the quality of the X-ray laser beam at the Department of Energy’s SLAC National Accelerator Laboratory. The meter-long mirrors are the ultimate in flatness, smooth to within the height of one atom or one-fifthof a nanometer [48] . Each mirror is made from an individual silicon crystal, artificially grown in a lab. After the mirror is polished with conventional techniques, the company uses a process called elastic emission machining, where a jet of ultra-pure water containing fine particles removes any remaining imperfections atom by atom. The same advanced technology may be used for the GIRR manufacturing.
An alternative method to long plane retro-reflectors is a nesting multiple GIRRs that also increases the collection area, and a thin metallic coating will further increase the critical angle and thus collection efficiency (see Figure 5).
7. The Discussion of GIRR Reflectivity Coefficients
We analyze below the solutions for vacuum stationary hard X-ray wave fields for the optimization of system design parameters and diffraction conditions that satisfy well the performance objectives of GIRR (see subsection 2.2).
Figure 5. A cascade of GIRRs. The extra-large-area retro-reflector is prepared using an array (or a mosaic) of individual large single-crystal wafers. Special processing techniques maintain the orientation of the individual crystals to very high accuracy. The angles 



7.1. GIXB by Bulk Germanium Wafer without Cover Layer
Let’s discuss a diffraction in case where the exact condition of coplanar GIXB holds inside bulk germanium wafer without cover layer, and the angle of incidence 



The reflectivity coefficients 



where n = 0, 1, 2, the function 





These graphs are computed using the values of the incidence angle 
Figure 6. The graphs of X-ray reflectivity coefficients and visibility of images depending on Bragg angle 

Equation (28a) can be rewritten in the following form using Equation (3):

where


The polarizability Fourier components







7.2. GIXB by Bulk Germanium Wafer Covered with Beryllium Layer
One may write the following relation between 


Since GIXB setup performs only if the magnitude of Bragg angle 



The diffraction angles can be determined through the system of analyzer crystals with an accuracy of at least
Here we analyze a particular case of coplanar GIXB by germanium single-crystal wafer covered with thin non-diffracting beryllium layer. Our goal is to find an opportunity to reduce the common reflected wave and increase the retro-reflected one.
The graphs of X-ray reflectivity coefficients





Figure 7. The graphs of X-ray reflectivity coefficients and visibility of images depending on Bragg angle 
Curves in Figure 7 correspond to the incident X-ray wavelength 






The coefficients


















The relation (30) can be rewritten in the following form:

Hence, a small changes of the cover layer thickness equal to 


The comparison of the corresponding graphs presented in Figure 6 and Figure 7 brings to the following relations:




The relation (32c) can be rewritten in the following form:

where j = 0, 1 (see Figure 7). The enhancement of retro-reflectivity coefficient of a single crystal wafer happens if it has a thin non-diffracting cover layer (see Equation (33)). This phenomenon is caused by the constructive interference between the X-ray wave field retro-reflected from crystal wafer and the X-ray waves multiply reflected from the top and bottom surfaces of the cover layer.
Now, let’s consider the X-ray reflectivity and retro-reflectivity coefficients and visibility function depending on the Bragg angle


Figure 8. The graphs of X-ray reflectivity coefficients and visibility of images depending on Bragg angle 
of the reflectivity graphs



We present below three-dimensional graphs of the retro-reflectivity and reflectivity coefficients, as well as the visibility function depending on both variables 
Figure 9. The retro-reflectivity coefficient.
Figure 10. The reflectivity coefficient.
Figure 11. The reflectivity coefficient if the Bragg condition is not satisfied.
Figure 12. The graph of visibility function.


where T is an arbitrary value of the cover layer thickness. Note that the maximums on oscillating graphs of reflectivity and retro-reflectivity coefficients and of visibility function correspond to kinematic Bragg angle 
7.3. Hard X-Ray Optical Noise and Background Filter
The modern laboratory X-ray source has a high intensity X-ray beam close to 109 photons s−1 focused on the sample surface by using a Cu rotating anode X-ray generator operated at 40 kV - 30 mA (1.2 kW), according to paper [52] . The design, implementation, and performance of an X-ray monochromator with ultra-high energy resolution of 
The images of non-diffracting nano-sized subsurface inclusions, obtained by the hard X-rays scattering process, show a high-intensity background, so, besides a sufficient intensity and energy resolution, the advanced hard X-ray image registration system needs an all-optical filter that removes unwanted background or optical noise from the conventional specular wave and essentially increases the visibility of the informative signal.
In the retro-reflection performance mode, a planar GIRR removes the primary radiation from the common reflected beam propagating in the direction of the wave vector 
Finally, we can conclude that single crystal wafer covered by a thin cover layer with a certain thickness performs like an X-ray optical noise (or background) filter. Moreover, simultaneously with the increase in the magnitude of the visibility function, a diminishing of certain effects occurs, for example, in the probability of data read-out errors and data read-out time during the digital data read-out procedure from X-ray optical data carrier preliminary covered by a thin non-diffracting protective layer [33] .
8. Conclusions
・ Proposed grazing-incidence retro-reflector (GIRR) is a plane mirror that totally reflects (or diffracts) the grazing-incidence hard X-ray photons back to its source.
・ The planar GIRR (or a cascade of GIRRs, see the subsection 6.5) consists of single-crystal wafer(s) covered by an ultra-thin, non-diffracting layer of low-absorbing material, and can be applied in hard X-ray optical noise (or background) filters, high-quality hard X-ray waveguides, low-gain hard X-ray free electron laser resonators (XFELRs), X-ray holography, coherent X-ray diffraction imaging, phase-con- trast imaging, as well as in hard X-ray optical data storage devices [32] [33] and deep space hard X-ray communications [6] - [9] .
・ The authors justify in Section 6 of this paper the selection of a germanium and beryllium material for the design of planar GIRR, as well as review the advanced nano-technologies of the present day through which the GIRR can be implemented.
・ Changes in thickness of cover layer bring to oscillations with slowly damping (relative to oscillations period) amplitude of the hard X-ray reflectivity and retro-reflec- tivity coefficients, as well as of the visibility function (see Figure 7 and Figures 9-12).
・ From the analysis of graphs presented in Figures 7-12, the authors conclude that the coplanar GIXB at a certain value of the Bragg angle 




・ The authors overcome a thermal expansion problem due to GIXB scheme, since the X-ray penetration depths in crystal wafer are at least in three orders smaller than in diffraction methods, which rely on normal-incidence Bragg reflectors. Also, the energy distribution of the primary beam along the crystal entrance surface is, at least, two orders of magnitude smaller in the case of grazing-incidence diffraction than the energy distribution for the same primary beam in the case of normal-incidence Bragg reflectors. These two circumstances clearly satisfy the requirement of keeping the crystal temperature precisely at a predefined level.
Cite this paper
Bezirganyan, H.J., Bezirganyan, R. and Bezirganyan, S. (2016) Planar Retro-Reflector for Grazing Incident Beam of High-Energy X-Ray Photons. Journal of Applied Mathematics and Physics, 4, 1731-1755. http://dx.doi.org/10.4236/jamp.2016.49181
References
- 1. Akiyama, T., Yoshida, N., Kawahata, K., Tokitani, M., Iwakiri, H., Okajima, S. and Nakayama, K. (2012) Studies of Reflectivity Degradation of Retroreflectors in LHD and Mitigation of Impurity Deposition Using Shaped Diagnostic Ducts and Protective Windows. Nuclear Fusion, 52, Article ID: 063014.
http://dx.doi.org/10.1088/0029-5515/52/6/063014 - 2. Schultz, P., Cumby, B. and Heikenfeld, J. (2012) Investigation of Five Types of Switchable Retroreflector Films for Enhanced Visible and Infrared Conspicuity Applications. Applied Optics, 51, 3744-3754.
http://dx.doi.org/10.1364/AO.51.003744 - 3. Ooi, C.H.R. (2010) Superintense Laser Fields from Multiple Laser Pulses Retro-Reflected in Circular Geometry. Journal of Applied Physics, 107, Article ID: 043110.
http://dx.doi.org/10.1063/1.3296128 - 4. Groswasser, D., Waxman, A., Givon, M., Aviv, G., Japha, Y., Keil, M. and Folman, R. (2009) Retroreflecting Polarization Spectroscopy Enabling Miniaturization. Review of Scientific Instruments, 80, Article ID: 093103.
http://dx.doi.org/10.1063/1.3213076 - 5. Dell’Agnello, S., Delle Monache, G., Vittori, R., Boni, A., Cantone, C., Ciocci, E., Martini, M., Patrizi, G., Tibuzzi, M., Bianco, G., Currie, D., Intaglietta, N., Salvatori, L., Lops, C., Contessa, S., Porcelli, L., Mondaini, C., Tuscano, P. and Maiello, M. (2015) Advanced Laser Retroreflectors for Astrophysics and Space Science. Journal of Applied Mathematics and Physics, 3, 218-227.
http://dx.doi.org/10.4236/jamp.2015.32032 - 6. Hemmati, H., Ed. (2006) Deep Space Optical Communications. JPL Deep Space Communications and Navigation Series. John Wiley & Sons Inc., Hoboken.
http://www.wiley.com/WileyCDA/WileyTitle/productCd-0470040025.html - 7. Arnon, S., Barry, J., Karagiannidis, G., Schober, R. and Uysaleds, M., Eds. (2012) Advanced Optical Wireless Communication Systems. Cambridge University Press, Cambridge. http://www.cambridge.org/9780521197878
- 8. Ghassemlooy, Z., Popoola, W.P. and Rajbhandari, S. (2013) Optical Wireless Communications: System and Channel Modelling with Matlab. CRC Press, Boca Raton.
https://www.crcpress.com/Optical-Wireless-Communications-System-and-Channel-
Modelling-with-MATLAB/Ghassemlooy-Popoola-Rajbhandari/p/book/9781439851883 - 9. Arnon, S. (Ed.) (2015) Visible Light Communication. Cambridge University Press, Cambridge.
http://www.cambridge.org/us/academic/subjects/engineering/communications-and-signal-processing/visible-light-communication?format=HB - 10. James, R.W. (1967) The Optical Principles of the Diffraction of X-Rays. Cornel University Press, Ithaca.
- 11. Azaroff, L.V., Kap-low, R., Kato, N., Weiss, R.J., Wilson, A.J.C. and Young, R.A. (1974) X-Ray Diffraction. In: Farnsworth, J.L. and Bradley, J.W., Eds., International Series in Pure and Applied Physics, McGraw-Hill Pub. Co., New York, 664 p.
- 12. Pinsker, Z.G. (1978) Dynamical Scattering of X-Rays in Crystals. Springer-Verlag, Berlin.
http://www.springer.com/us/book/9783642812095 - 13. Authier, A. (2001) Dynamical Theory of X-Ray Diffraction. Oxford University Press, Oxford.
https://global.oup.com/academic/product/dynamical-theory-of-X-ray-diffraction-9780198528920?lang=en&cc=us - 14. Kohra, K. and Matsushita, T. (1972) Some Characteristics of Dynamical Diffraction at a Bragg Angle of about π/2. Zeitschrift für Naturforschung, 27, 484-487.
http://zfn.mpdl.mpg.de/data/Reihe_A/27/ZNA-1972-27a-0484.pdf
http://dx.doi.org/10.1515/zna-1972-0317 - 15. Brümmer, O., Höche, H.R. and Nieber, J. (1979) X-Ray Diffraction in the Bragg Case at Bragg Angles of about π/2. Physica Status Solidi (A), 53, 565-570.
http://dx.doi.org/10.1002/pssa.2210530220 - 16. Graeff, W. and Materlik, G. (1982) Millielectron Volt Energy Resolution in Bragg Backscattering. Nuclear Instruments and Methods in Physics Research, 195, 97-103.
http://dx.doi.org/10.1016/0029-554X(82)90764-9 - 17. Caticha, A. and Caticha-Ellis, S. (1982) Dynamical Theory of X-Ray Diffraction at Bragg Angles Near π/2. Physical Review B, 25, 971-983.
http://dx.doi.org/10.1103/PhysRevB.25.971 - 18. Sutter, J.P., Alp, E.E., Hu, M.Y., Lee, P.L., Sinn, H., Sturhahn, W. and Toellner, T.S. (2001) Multiple-Beam X-Ray Diffraction Near Exact Backscattering in Silicon. Physical Review B, 63, Article ID: 094111.
http://dx.doi.org/10.1103/physrevb.63.094111 - 19. Caticha, A., Aliberti, K. and Caticha-Ellis, S. (1996) A Fabry-Perot Interferometer for Sub-meV X-Ray Energy Resolution. Review of Scientific Instruments, 67, 3380-3381.
http://dx.doi.org/10.1063/1.1147321 - 20. Liss, K.-D., Hock, R., Gomm, M., Waibel, B., Magerl, A., Krisch, M. and Tucoulou, R. (2001) X-Ray Photon Storage in a Crystal Cavity. In: Mills, D.M., Schulte-Schrepping, H. and Arthur, J.R., Eds., X-Ray FEL Optics and Instrumentation, SPIE Press, Bellingham, 78-88.
http://dx.doi.org/10.1117/12.413682 - 21. Chang, S.-L., Stetsko, Y.P., Tang, M.-T., Lee, Y.-R., Sun, W.-H., Yabashi, M. and Ishikawa, T. (2005) X-Ray Resonance in Crystal Cavities: Realization of Fabry-Perot Resonator for Hard X-Rays. Physical Review Letters, 94, Article ID: 174801.
http://dx.doi.org/10.1103/physrevlett.94.174801 - 22. Chang, S.-L., Stetsko, Y.P., Tang, M.-T., Lee, Y.-R., Sun, W.-H., Yabashi, M., Ishikawa, T., Wu, H.-H., Shew, B.-Y., Lin, Y.-H., Kuo, T.-T., Tamasaku, K., Miwa, D., Chen, S.-Y., Chang, Y.-Y. and Shy, J.-T. (2006) Crystal Cavity Resonance for Hard X Rays: A Diffraction Experiment. Physical Review B, 74, Article ID: 134111.
http://dx.doi.org/10.1103/physrevb.74.134111 - 23. Wu, Y.-H., Tsai, Y.-W., Chu, C.-H., Liu, W.-C., Chang, Y.-Y. and Chang, S.-L. (2015) Inclined-Incidence Hard-X-Ray Resonator with Ultrahigh Efficiency and Resolution. Optics Express, 23, 9994-10001.
http://dx.doi.org/10.1364/OE.23.009994 - 24. Tsai, Y.-W., Wu, Y.-H., Chang, Y.-Y., Liu, W.-C., Liu, H.-L., Chu, C.-H., Chen, P.-C., Lin, P.-T., Fu, C.-C. and Chang, S.-L. (2016) Sapphire Hard X-Ray Fabry-Perot Resonators for Synchrotron Experiments. Journal of Synchrotron Radia-tion, 23, 658-664.
http://dx.doi.org/10.1107/S1600577516004999 - 25. Caticha, A. and Cati-cha-Ellis, S. (1990) A Fabry-Perot Interferometer for Hard X-Rays. Physica Status Solidi (A), 119, 643-654.
http://dx.doi.org/10.1002/pssa.2211190228 - 26. Huang, X.R., Siddons, D.P., Ma-crander, A.T., Peng, R.W. and Wu, X.S. (2012) Multicavity X-Ray Fabry-Perot Resonance with Ultrahigh Resolution and Contrast. Physical Review Letters, 108, Article ID: 224801.
http://dx.doi.org/10.1103/physrevlett.108.224801 - 27. Bergamin, A., Cavagnero, G., Mana, G. and Zosi, G. (1999) Scanning X-Ray Interferometry and the Silicon Lattice Parameter: Towards Relative Uncertainty? European Physical Journal B, 9, 225-232.
http://dx.doi.org/10.1007/s100510050760 - 28. Ferroglio, L., Mana, G. and Massa, E. (2008) Si Lattice Parameter Measurement by Centimeter X-Ray Interferometry. Optics Express, 16, 16877-16888.
http://dx.doi.org/10.1364/OE.16.016877 - 29. Massa, E., Mana, G., Kuetgens, U. and Ferroglio, L. (2011) Measurement of the {2 2 0} Lattice-Plane Spacing of a 28Si X-Ray Interferometer. Metrologia, 48, S37-S43.
http://dx.doi.org/10.1088/0026-1394/48/2/S06 - 30. Bezirganyan, H.P. and Bezirganyan, P.H. (1988) Solution of the Two-Dimensional Stationary Schrödinger Equation with Cosine-Like Coefficient (In View of X-Ray Diffraction). Physica Status Solidi (A), 105, 345-355.
http://dx.doi.org/10.1002/pssa.2211050205 - 31. Bezirganyan, H.P. (1988) X-Ray Reflection from and Transmission through a Plane-Parallel Dielectric Plate with Cosine-Like Polarizability (Symmetrical Laue Case). Physica Status Solidi (A), 109, 101-110.
http://dx.doi.org/10.1002/pssa.2211090109 - 32. Bezirganyan, H.P., Bezirganyan Jr., H.H., Bezirganyan, S.E. and Bezirganyan Jr., P.H. (2004) Specular Beam Suppression and Enhancement Phenomena in the Case of Grazing-Angle Incidence X-Rays Back Diffraction by the Crystal with Stacking Fault. Optics Communications, 238, 13-28.
http://dx.doi.org/10.1016/j.optcom.2004.04.038 - 33. Bezirganyan, H.P., Bezirganyan Jr., H.H., Bezirganyan, S.E., Bezirganyan Jr., P.H. and Mossikyan, Y.G. (2005) An Ultrahigh-Density Digital Data Readout Method Based on Grazing-Angle Incidence X-Ray Backscattering Diffraction. Journal of Optics A: Pure and Applied Optics, 7, 604-612.
http://dx.doi.org/10.1088/1464-4258/7/10/013 - 34. Yu, X. and Fan, S. (2004) Anomalous reflections at photonic crystal surfaces. Phys. Rev. E, 70, Article ID: 055601.
http://dx.doi.org/10.1103/physreve.70.055601 - 35. Floquet, G. (1883) Sur les équations différentielles linéaires à coefficients périodiques. Annales Scientifiques de l’école Normale Supérieure,12, 47-88.
http://www.numdam.org/item?id=ASENS_1883_2_12__47_0 - 36. Bloch, F. (1928) über die Quantenmechanik der Elektronen in Kristallgittern. Zeitschrift für Physik, 52, 555-600.
http://www.pwein.at/physics/Lectures/Famous-Papers/Z-Physik-52-555-1928.pdf
http://dx.doi.org/10.1007/BF01339455 - 37. Mathieu, E. (1868) Memoire sur le Mouvement Vibratoire d’une Membrane de Forme Elliptique. Journal de Mathématiques Pures et Appliquées, 13, 137-203.
https://eudml.org/doc/234720 - 38. McLachlan, N.W. (1947) Theory and Application of Mathieu Functions. Oxford University Press, London.
https://www.amazon.com/Theory-Application-Mathieu-Functions-McLachlan/dp/
B0007DMXT6 - 39. Meixner, J., Schaefke, F.W. and Wolf, G. (1980) Mathieu Functions and Spheroidal Functions and Their Mathematical Foundations. Springer, Berlin.
http://dx.doi.org/10.1007/BFb0096194 - 40. Shiraishi, Y., Takano, K., Matsubara, J., Iida, T., Takase, N., Machida, N., Kuramoto, M. and Yamagishi, H. (2001) Growth of Silicon Crystal with a Diameter of 400 mm and Weight of 400 kg. Journal of Crystal Growth, 229, 17-21.
http://dx.doi.org/10.1016/S0022-0248(01)01042-9 - 41. Yamagishi, H., Kuramoto, M., Shiraishi, Y., Machida, N., Takano, K., Takase, N., Iida, T., Matsubara, J., Minami, H., Imai, M. and Takada, K. (1999) Large Diameter Silicon Technology and Epitaxy. Microelectronic Engineering, 45, 101-111.
http://dx.doi.org/10.1016/S0167-9317(99)00106-9 - 42. Claeys, C. and Simoen, E. (2009) Extended Defects in Germanium: Fundamental and Technological Aspects. Springer, Berlin, Heidelberg.
http://link.springer.com/book/10.1007/978-3-540-85614-6
http://dx.doi.org/10.1007/978-3-540-85614-6 - 43. Tanner, B.K., Wittge, J., Vagovic, P., Baumbach, T., Allen, D., McNally, P.J., Bytheway, R., Jacques, D., Fossati, M.C., Bowen, D.K., Garagorri, J., Elizalde, M.R. and Danilewsky, A.N. (2013) X-Ray Diffraction Imaging for Predictive Metrology of Crack Propagation in 450-mm Diameter Silicon Wafers. Powder Diffraction, 28, 95-99.
http://dx.doi.org/10.1017/S0885715613000122 - 44. Van Hemmen, J.L., Heil, S.B.S., Klootwijk, J.H., Roozeboom, F., Hodson, C.J., van de Sanden, M.C.M. and Kessels, W.M.M. (2007) Plasma and Thermal ALD of Al2O3 in a Commercial 200 mm ALD Reactor. Journal of the Electrochemical Society, 154, G165-G169. http://jes.ecsdl.org/content/154/7/G165
http://dx.doi.org/10.1149/1.2737629 - 45. Lu, Z., et al. (2013) Effects of High Temperature Rapid Thermal Annealing on Ge Films Grown on Si(001) Substrate. Chinese Physics B, 22, Article ID: 116804.
http://dx.doi.org/10.1088/1674-1056/22/11/116804 - 46. Walsh, K.A. (2009) Beryllium Chemistry and Processing. ASM International, USA, 183.
http://www.asminternational.org/search/-/journal_content/56/10192/05223G/PUBLICATION - 47. JTEC Corporation. Development and Production of Optical Mirrors for Synchrotron Radiation. Japan. http://j-tec.co.jp/english/index.html
- 48. The X-Ray Mirrors That Differ by One Atom in Flatness from End to End. SLAC National Accelerator Laboratory News.
https://www6.slac.stanford.edu/news/2016-08-01-perfection-sight-slac-receives-new-mirrors-x-ray-laser.aspx - 49. Szwacki, N.G. and Szwacka, T. (2015) Basic Elements of Crystallo-graphy. Pan Stanford Publishing Pte. Ltd., Singapore. http://www.panstanford.com/books/9789814613576.html
- 50. Martienssen, W. and Warlimont, H., Eds. (2005) Springer Handbook of Condensed Matter and Materials Data. Springer, Berlin.
http://www.springer.com/us/book/9783540304371
http://dx.doi.org/10.1007/3-540-30437-1 - 51. Kohn, V.G. (2006) Program for Calculating the Scattering Parameters Used in the X-Ray Standing Wave Method. Crystallography Reports, 51, 936-940.
http://link.springer.com/article/10.1134%2FS1063774506060034
http://dx.doi.org/10.1134/S1063774506060034 - 52. Omote, K. (2010) High Resolution Grazing-Incidence In-Plane X-Ray Diffraction for Measuring the Strain of a Si Thin Layer. Journal of Physics: Condensed Matter, 22, Article ID: 474004.
http://dx.doi.org/10.1088/0953-8984/22/47/474004 - 53. Yabashi, M., Tamasaku, K., Kikuta, S. and Ishikawa, T. (2001) X-Ray Monochromator with an Energy Resolution of 8 × 10?9 at 14.41 keV. Review of Scientific Instruments, 72, 4080-4083.
http://dx.doi.org/10.1063/1.1406925

*The paper is devoted to memory of Prof. Dr. Petros Bezirganyan (1916-1994). Towards the 100th Anniversary of his birthday on 15th December 2016.













