Received 30 March 2016; accepted 20 May 2016; published 23 May 2016

ABSTRACT

A recent study illustrates an exciting new element of bacteria-host interactions in which the opportunistic pathogen Pseudomonas aeruginosa quorum sensing signal molecule can modulate the host immune system. In this paper, on the basic of a model which describes the competition between bacteria and immune system, a mathematical model is proposed to investigate the modulation of quorum sensing signal molecule on immune response. It is shown that the modulation leads to a backward bifurcation and some more new dynamical behaviors. By numerical simulations, we find a fold bifurcation of equilibria, which induces three patterns of dynamical behaviors including the bistable phenomenon. Our model quantifies the modulation of quorum sensing signal molecule on the immune response, which may provide a therapy for bacteria infections.

Keywords:

Pseudomonas aeruginosa, Quroum Sensing, Modulation, Bifurcation

1. Introduction

Pseudomonas aeruginosa (abbr. P. aeruginosa) is an increasingly prevalent opportunistic human pathogen capable of causing a broad range of acute and chronic infections. It is a common gram-negative bacterium in nosocomial infection, and commonly found in soil and water. P. aeruginosa can cause severe disease in animals and humans and infect the hosts with defective immune system function, such as those with burns, neutropenic cancer and bone marrow transplant patients [1] . These infections are difficult to treat using conventional antibiotic therapies and often result in considerable morbidity and mortality [2] . One of the reasons that P. aeruginosa produces such diverse, often overwhelming infections is due to an array of virulence factors, including elastase, alkaline protease, exotoxin A, lipase, pyocyanin, and rhamnolipid, which are capable of causing tissue damage and promoting systemic dissemination and interfering with immune clearance mechanisms. Several studies in models of burn wound infection and pneumonia have demonstrated that the virulence factors are regulated in a cell density dependent process termed quorum sensing [3] . Recently, studies have shown that P. aeruginosa quorum sensing signal molecule (abbr. QSSM) can not only help bacteria adapt to the environment but also they contribute to the pathogenesis of P. aeruginosa infections by acting as virulence factors per se. Apart from this, previous data have demonstrated that the quorum sensing signal molecules themselves have immunomodulatory activity, which means that P. aeruginosa can tailor the host immune response [4] . Particular, 3-O-C12-HSL stimulates various host signaling pathways to inhibit or activate immune cell responses, and recently, Bortolotti et al. [5] observe that 3-O-C12-HSL is able to induce HLA-G expression in human monocytes and T cells to control the host immune response.

The theoretical study of bacteria-immune dynamics in the aspect of immunology has a long history. Majority mathematical models have been formulated to study the bacteria-immune dynamics behavior. For example, Fergola et al. [6] firstly constructed an ODEs model to characterize the competition between bacteria and innate immune system, and found that the quorum sensing term in the model significantly influenced the stability of the meaningful steady-state solutions. Zhang et al. [7] [8] formulated delay differential equations (abbr. DDEs) to find that Hopf bifurcation occurred for a long enough time delay, and formulated ODEs by identifying the nonlinear function to characterize quorum sensing to study the intervention of quorum in the competition between bacteria and the immune system.

The purpose of the present paper is to develop a mathematical model to depict the influence of quorum sensing signal molecule on the competition between bacteria and immune system. We provide theoretical analysis and numerical simulations to investigate the influence of QSSM on bacteria infection. We find that the influence of QSSM leads to backward bifurcation, multiple positive equilibrium and patterns of bistability, which may be helpful for immunotherapy.

For this paper, it is organized as follows. We introduce the mathematic model in Section 2, and explore the analysis of the model for mathematical and biological implications in Section 3. We present the numerical simulation in Section 4. Section 5 provides the conclusion and discussion.

2. Model Formulation

Denote the concentrations of the bacteria, quorum sensing signal molecule, and immune cells, as respectively. Suppose the dynamic relations among them are as the following: the bacteria grow logistically at rate a with the effective carrying capacity of environment k, and it is cleared by immunity (mass action term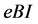). The immune cells have a source term and a half-life term denoted by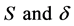, and S represents that the memory cells are present and includes a wide range of cells involved in the first wave of defense of the host. The immune cells are increased by signals captured by the bacteria load.

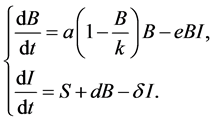(1)

The background production of quorum sensing signal molecule is 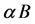and the natural degeneration rate is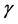. Considering the effect of quorum sensing on the competition between bacteria and innate immune system, we have been known that quorum sensing signal molecule could modulate immune response. Here, similar with the methods in [9] , we introduce the following:

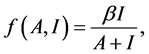
which represents the modulation of quorum sensing signal molecule between bacteria and immune response.

Taking all of the above into considerations, we obtain the following model.

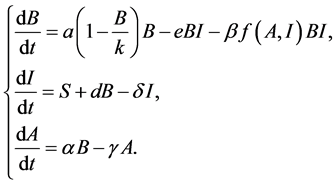(2)

As we know, only a certain threshold concentration of quorum sensing signal molecule is exceeded, the bacteria can change their behavior by gene transcription induction. Then, the bacteria have ability to infect host. So we assume the quorum sensing signal molecule to be in a quasi-steady state such that 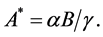Then, we could obtain the competition model between bacteria and the immune system.

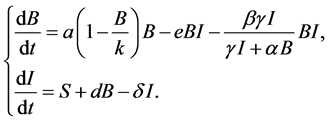(3)

The basic reproduction number of (3) is

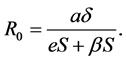
Setting then 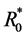is the basic reproduction number of (1). It is shown in [6] that the dynamical beha-

viors of system (1) are completely determined by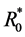, specifically, the boundary equilibrium 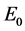is globally asymptotically stable if, and if, system (1) exists a unique positive equilibrium and it is locally asymptotically stable. Here, we illustrate the impact of QSSM on the infection of bacteria to immune system and rich dynamical behaviors in (3). This research maybe provides insights for medicine to fight bacteria infection.

3. Equilibria and Bifurcation

There always has a bacteria free equilibrium where. Evaluating the Jacobi matrix of sys-

tem (3) at the bacteria free equilibrium is

thus, by the Routh-Hurwitz criterion, we have

Theorem 1. The bacteria free equilibrium is locally asymptotically stable if while if the bacteria free equilibrium is unstable.

Next let us discuss the existence and stability of positive equilibria. Let be the positive equilibrium of system (3). We have

(4)

From second equation in Equation (4), it follows that where is a positive solution of the following equation

(5)

in which

Note that is equivalent to

(6)

For positive equilibria to exist, the solutions of Equation (5) must be positive. Note that and has the same sign as. It follows that system (3) admits a unique positive equilibrium if.

Next, we put our attention on finding positive equilibria of system (3) when. Specially, when, then, consequently, system (3) has a unique positive equilibrium.

Let, we have and. There-

fore, when, there is a unique such that. Thus, we could obtain the following results on the existence of the positive equilibria of system (3).

Theorem 2.

1) There exists a unique positive equilibrium if while if there has a unique positive equilibrium and also, there has a unique positive equilibrium if and

2) There are two positive equilibria and if and.

3) There not exists any positive equilibrium if one of the following conditions holds:

i),; ii) and.

where with and whose components given by

Remark 1. From the expression of, we know that when,

Then system (3) changes to the system (1), where we could see that a forward bifurcation exhibits in system (3) when. While the epidemiological implication of Remark 1 is that, if is equal to zero, when, there only exists a bacteria-free equilibrium, which means the infection of bacteria to host immune system will die out. Furthermore, the infection will persist when. However, if, we will show in the following parts that the infection may persist if.

Theorem 2 indicates that system (3) exhibits multiple positive equilibria via a backward bifurcation. Then we have the following:

Theorem 3. There exhibits a backward bifurcation at whenever.

Proof: Let

Choosing as a bifurcation parameter, solving, then we have. The jacobian matrix

at the bacteria free equilibrium with is

then, the characteristic roots are

Denote, a right eigenvector corresponding to zero eigenvalue, then,

With, then

Furthermore, the left eigenvector satisfying is. By computing the second- order partial derivatives of at the disease-free equilibrium, we obtain

and their cross derivatives are coincide. Moreover,

and the other second-order partial derivatives of at the disease-free equilibrium are equal to zero.

According to coefficients and defined in Theorem4.1 of Castillo-Chavez and Song [10] , it follows that

and

Obviously, the coefficient is positive. When, is positive. It follows that

model (3) undergoes a backward bifurcation at whenever.

So a backward bifurcation occurs at with, we can point out that when, if

becomes stronger than some level, the backward bifurcation will take place. Thus, we could say is one of the factors which lead to the backward bifurcation.

4. Numerical Simulation

In this section, we implement numerical simulations based on the theoretical results above for the purpose of clear understanding of the complex dynamical behavior of system (3) and explore more patterns of dynamical behaviors of model (3).

Example 1. When we choose, with the value of other parameters as following, , , , then system (3) changes to system (1), a forward bifurcation occurs when.

A forward bifurcation is shown in Figure 1, where and is a bifurcation parameter. With the help of the Matcont package [11] , we obtain some more complicated dynamical behaviors of system (3). We endow values to the parameters of system (3) in Table 1, some of them are chosen from literatures.

Choosing as a bifurcation parameter, we observe a backward bifurcation, which occurs through the branch point (BP) at, where and. In addition, we find a fold bifurcation

point (LP) at, where

Hence, from Figure 2 we conclude that if we increase from zero continuously, we can obtain the three typical patterns of dynamical behaviors are listed in Table 2, which could support the Theorem 3.

Firstly, if, then is relatively small, that is, there only exists a bacteria-free equilibrium and it is locally asymptotically stable. Figure 3 shows this pattern where the parameter is chosen as 0.1 (), the numerical solution of system (3) with the initial condition tends to the bacteria free equilibrium as time tends to infinity.

Secondly, if, then becomes a little large, but it still smaller than one. The bacteria-free equilibrium still exists and coexists with two positive equilibria, and the large one positive equilibrium is stable while the smaller is unstable. Hence, the bistability occurs, where a stable bacteria-free equilibrium coexists with a stable positive equilibrium. For this pattern, we choose () to obtain Figure 4 and Figure 5, where with the initial condition , the solution tend to bacteria-free equilibrium while the solution with initial condition tends to the stable positive equilibrium. We shows the orbit in Figure 6, where we could easily see the bistability phenomena.

Thirdly, if, then, where the stable bacteria-free equilibrium becomes unstable. There only exists a stable positive equilibrium. For this pattern, we choose (). In Figure 7, the solution with the initial condition tends to the stable positive equilibrium.

5. Conclusion and Discussion

In this paper, we have developed a mathematical model based on the model which describes the competition between bacteria and immune system to illustrate the influence of quorum sensing signal molecule on the competition between bacteria and immune system. In order to simplify the model, we make an assumption that quorum sensing signal molecules have reached a steady state when they modulate the immune response during the bacteria infection. By combing qualitative analysis and numerical simulations, comparing with the results in

model (1), we find our model can exhibit some new and complicated dynamical behaviors. We observe that if we neglect the modulation of quorum sensing signal molecule to immune response, that is,. Then our model becomes to the model (9) in [6] , where the bacteria-free equilibrium is globally asymptotically stable if the basic reproduction number is smaller than one, which means, in this case, the bacteria will be cleared if Actually, due to the modulation of quorum sensing signal molecule or the influence of quorum sensing signal

molecule on the competition between bacteria and immune system, bacteria infection becomes complicated.

From our model, we find some interesting results that the model can exhibit three different patterns of dynamical behaviors if we choose as bifurcation parameter. When is relatively small, where it is smaller than, the bacteria-free equilibrium is asymptotically stable, then the bacteria will die out. However, when

, except for a stable bacteria-free equilibrium, there also have a stable positive equilibrium and an unstable positive equilibrium, thus, the bistability occurs in this case, where the bacteria may exist. If is large enough, when it is larger than 1, the model admits a unique stable positive equilibrium, the bacteria exist in human body.

According to the mathematical analysis and numerical simulations of the model proposed in this paper, it may provide new insights to fight the bacteria infection. It is interesting to find a way to inhibit the modulation, so that we can find an available way to defeat bacteria infection. We act this work as our future goal.

Cite this paper

Zhiwen Zhang, (2016) Mathematical Model of a Bacteria-Immunity System with the Influence of Quorum Sensing Signal Molecule. Journal of Applied Mathematics and Physics,04,888-896. doi: 10.4236/jamp.2016.45097

References