Journal of Applied Mathematics and Physics
Vol.04 No.02(2016), Article ID:63627,10 pages
10.4236/jamp.2016.42033
Analytical and Traveling Wave Solutions to the Fifth Order Standard Sawada-Kotera Equation via the Generalized 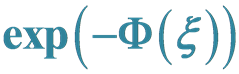 -Expansion Method
-Expansion Method
M. Y. Ali*, M. G. Hafez, M. K. H. Chowdury, M. T. Akter
Department of Mathematics, Chittagong University of Engineering and Technology, Chittagong, Bangladesh

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).



Received 14 December 2015; accepted 19 February 2016; published 22 February 2016
ABSTRACT
In this article, we propose a generalized 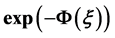 -expansion method and successfully implement it to find exact traveling wave solutions to the fifth order standard Sawada-Kotera (SK) equation. The exact traveling wave solutions are established in the form of trigonometric, hyperbolic, exponential and rational functions with some free parameters. It is shown that this method is standard, effective and easily applicable mathematical tool for solving nonlinear partial differential equations arises in the field of mathematical physics and engineering.
-expansion method and successfully implement it to find exact traveling wave solutions to the fifth order standard Sawada-Kotera (SK) equation. The exact traveling wave solutions are established in the form of trigonometric, hyperbolic, exponential and rational functions with some free parameters. It is shown that this method is standard, effective and easily applicable mathematical tool for solving nonlinear partial differential equations arises in the field of mathematical physics and engineering.
Keywords:
Generalized 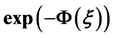 -Expansion Method, Fifth Order Standard Sawada-Kotera Equation, Solitons, Periodic Wave Solutions
-Expansion Method, Fifth Order Standard Sawada-Kotera Equation, Solitons, Periodic Wave Solutions

1. Introduction
The nonlinear partial differential equations (NPDEs) are widely used as model equations to study on the dynamics of many issues concerning in the field of mathematical physics, chemistry and engineering. Therefore, it is necessary to solve them analytically or numerically. Some of the methods to solve them analytically are the Hirota method [1] , the projective Riccati equation method [2] , the homogeneous balance method [3] - [5] , the tanh-function method [6] - [10] , the exp-function method [11] , the improved F-expansion method [12] , the
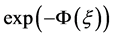 -expansion method [13] - [19] , sine-cosine method [20] , the modified simple equation method [21] , the
-expansion method [13] - [19] , sine-cosine method [20] , the modified simple equation method [21] , the 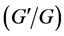 -expansion method [22] [23] , the modified extended tanh-function method with Riccati equation [24] and others. In the references [13] - [19] , we observe that the
-expansion method [22] [23] , the modified extended tanh-function method with Riccati equation [24] and others. In the references [13] - [19] , we observe that the 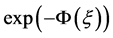 -expansion method provides only few solutions according to the nonlinear ordinary differential equation (ODE)
-expansion method provides only few solutions according to the nonlinear ordinary differential equation (ODE) . There
. There
are a lot of previous literature, where the researchers have investigated exact travelling wave solutions to the NPDEs using the 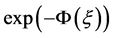 -expansion method. But there is no work to clarify why the coefficient of
-expansion method. But there is no work to clarify why the coefficient of  to the subsidiary equation is unity. This is the disadvantage of this method. Recently, Hafez and Akbar [25] have developed an exponential expansion method to solve NLPDEs by considering three auxiliary
to the subsidiary equation is unity. This is the disadvantage of this method. Recently, Hafez and Akbar [25] have developed an exponential expansion method to solve NLPDEs by considering three auxiliary
equations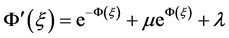 ,
, 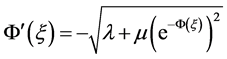 and
and . Form this literature, we observe that the NLPDEs has almost similar types of solutions with the help of
. Form this literature, we observe that the NLPDEs has almost similar types of solutions with the help of 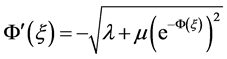 and
and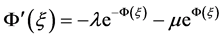 . This is a good technique, but it is taking too much time for solving nonlinear evaluation equations. Recently, Hafez and Lu [26] have proposed a generalized
. This is a good technique, but it is taking too much time for solving nonlinear evaluation equations. Recently, Hafez and Lu [26] have proposed a generalized 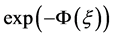 -expansion method for investigating the traveling wave solutions of the nonlinear fractional partial
-expansion method for investigating the traveling wave solutions of the nonlinear fractional partial
differential equations. We have proposed this method for solving NPDEs. On the other hand, through the proposed method, not only re-derives all known solutions in a systemic way but also delivers several exact traveling wave solutions to the NPDEs found by influence of the related free parameters if the nonlinear ODE

There is an amount of article [27] - [32] , where the exact solutions of the standard SK equation are analyzed. Some exact solutions of the standard SK equation have been evaluated using different methods, such as the tanh-coth method [29] , generalized the tanh-coth method [30] and the exp-function method [31] . The aim of this article is to establish the advance exponential expansion method and linking the method for evaluating the exact traveling wave solutions to the standard SK equation. The advantage of the proposed method over the other existing methods is that it provides new exact traveling wave solutions to the nonlinear PDEs. This article also
shows that the proposed method is very effective and standard technique rather than the 

2. The Methodology
The traveling wave solutions of a nonlinear evolution equation in one space dimensional are solutions obtained by assuming

where k is the wave number is and V is the speed of the wave.
The method consists of writing the traveling wave solution in the following form:

where the coefficients 


where




This substitution results in a scaling of the coefficients of the expansion for


The value of the positive integer N can be determined by balancing the highest order derivative term with the nonlinear term of the highest order appearing in the reducing ODE according to the traveling wave variables transformation. By substituting (1) into the reduce ODE by means of Equation (2), we can easily obtain a system
of algebraic equations for

3. Application of the Method
In this section, the application of the proposed method to extract more explicit and exact traveling wave solutions to the fifth order standard SK equation has been presented. The general form of an evolution equation with same scaling properties as the KdV [29] [30] is

where a, b and c are arbitrary nonzero real parameters and 
In this article, we have considered the following standard SK equation [31] :

which is the special case of Equation (5). It is known that the SK equation belongs to the completely integrable hierarchy of higher-order model evolution equations and has many sets of conservation laws [32] - [34] . Here 

where V is the speed of traveling wave, then we can be reduced the Equation (6) in to the following ODE:

Integrating (8) with respect to

where prime denotes derivative with respect to 




By substituting (10) into (9) and using the Equation (3), we obtain a set of algebraic equations by equating the coefficients of

Set 1: 




Set 2:




When
For Set 1:





where 

For Set 2:





where 

When
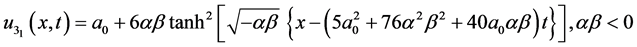








From the solutions (11)-(29), we observe that the proposed advance exponential expansion method scheme relating to the subsidiary equation gives more valuable explicit form solutions to the standard SK equation.
4. Comparison between Matinfar et al. [31] Solutions and Our Obtained Solutions
Matinfar et al. [31] have investigated the solutions of the fifth order standard Sawada-Kotera equation using the exp-function method to the following forms
On the other hand, twenty solutions including Matinfar et al. [31] solutions are constructed of this equation by applying the generalized expansion method. It is noteworthy to observe that the obtained solutions are new, realistic and applicable to practical problems. The auxiliary equation used in this paper is different, so obtained solutions is also different. It can be shown that this method is easier than other methods and applicable to other nonlinear evolution equations.
5. Physical Explanations
This section represents the physical explanations of the above determined solutions of the standard SK equations. The fifth order standard SK equation is an important model equation that appeared for describing several types of wave propagation such gravity-capillary waves, the propagation of shallow water waves over a flat surface and magneto-sound wave propagation in plasmas. It contains nonlinear terms and dispersive terms, so the solitary wave solutions of this equation have investigated. The solitary wave is a wave which propagates without any temporal evolution in shape or size when viewed in the reference frame moving with the group velocity of the wave. From the above determined solutions, we observe that the advance 
Figure 1 displays the exact conidal soliton like wave profile according to the solution 



































Figure 1. Surface plot of exact soliton like solitary wave solution.
Figure 2. Surface plot of exact multiple soliton like solitary wave solution.
Figure 3. Surface plot of exact cuspon like solitary wave solution.
Figure 4. Surface plot of exact compacton like solitary wave solutions.
Figure 5. Surface plot of soliton type solitary wave solution.
Figure 6. Surface plot of exact bell like solitary wave solution.
Figure 7. Surface plot of exact periodic traveling wave solution.
Figure 8. Surface plot of exact singular soliton type solitary wave solution.

6. Conclusion
In this article, the generalized 

Cite this paper
M. Y.Ali,M. G.Hafez,M. K. H.Chowdury,M. T.Akter, (2016) Analytical and Traveling Wave Solutions to the Fifth Order Standard Sawada-Kotera Equation via the Generalized exp(-Φ(ξ))-Expansion Method. Journal of Applied Mathematics and Physics,04,262-271. doi: 10.4236/jamp.2016.42033
References
- 1. Hirota, R. (1971) Exact Solution of the KdV Equation for Multiple Collisions of Solutions. Physical Review Letters, 27, 1192-1194.
http://dx.doi.org/10.1103/PhysRevLett.27.1192 - 2. Yan, Z. (2003) Generalized Method and Its Application in the Higher-Order Nonlinear Schrodinger Equation in Nonlinear Optical Fibres. Chaos, Solitons & Fractals, 16, 759-766.
http://dx.doi.org/10.1016/S0960-0779(02)00435-6 - 3. Zhao, X. and Tang, D. (2002) A New Note on a Homogeneous Balance Method. Physics Letters A, 297, 59-67.
http://dx.doi.org/10.1016/S0375-9601(02)00377-8 - 4. Zhao, X., Wang, L. and Sun, W. (2006) The Repeated Homogeneous Balance Method and Its Applications to Nonlinear Partial Differential Equations. Chaos, Solitons & Fractals, 28, 448-453.
http://dx.doi.org/10.1016/j.chaos.2005.06.001 - 5. Zhaosheng, F. (2004) Comment on “On the Extended Applications of Homogeneous Balance Method. Applied Mathematics and Computation, 158, 593-596.
http://dx.doi.org/10.1016/j.amc.2003.10.003 - 6. Malfliet, W. and Hereman, W. (1996) The Tanh Method: I. Exact Solutions of Nonlinear Evolution and Wave Equations. Physica Scripta, 54, 563-568.
http://dx.doi.org/10.1088/0031-8949/54/6/003 - 7. Abdou, M.A. and Soliman, A.A. (2006) Modified Extended Tanh-Function Method and Its Application on Nonlinear Physical Equations. Physics Letters A, 353, 487-492.
http://dx.doi.org/10.1016/j.physleta.2006.01.013 - 8. Abdou, M.A. (2007) The Extended Tanh-Method and Its Applications for Solving Nonlinear Physical Models. Applied Mathematics and Computation, 190, 988-996.
http://dx.doi.org/10.1016/j.amc.2007.01.070 - 9. Wazwaz, A.M. (2008) The Extended Tanh Method for New Compact and Noncompact Solutions for the KP-BBM and the ZK-BBM Equations. Chaos, Solitons & Fractals, 38, 1505-1516.
http://dx.doi.org/10.1016/j.chaos.2007.01.135 - 10. El-Wakil, S.A. and Abdou, M.A. (2007) New Exact Travelling Wave Solutions Using Modified Extended Tanh-Function Method. Chaos, Solitons & Fractals, 31, 840-852.
http://dx.doi.org/10.1016/j.chaos.2005.10.032 - 11. He, J.H. and Wu, X.H. (2006) Exp-Function Method for Nonlinear Wave Equations. Chaos, Solitons Fractals, 30, 700-708.
http://dx.doi.org/10.1016/j.chaos.2006.03.020 - 12. Wang, W. and Zhang, H.Q. (2005) Further Improved F-Expansion Method and New Exact Solutions of Konopelchenko-Dubrovsky Equation. Chaos, Solitons Fractals, 25, 601-610.
http://dx.doi.org/10.1016/j.chaos.2004.11.026 - 13. Hafez, M.G., Alam, M.N. and Akbar, M.A. (2015) Traveling Wave Solutions for Some Important Coupled Nonlinear Physical Models via the Coupled Higgs Equation and the Maccari System. Journal of King Saud University—Science, 27, 105-112. http://dx.doi.org/10.1016/j.jksus.2014.09.001
- 14. Hafez, M.G., Kauser, M.A. and Akter, M.T. (2014) Some New Exact Travelling Wave Solutions for the Zhiber-Shabat Equation. British Journal of Mathematics & Computer Science, 4, 2582-2593.
http://dx.doi.org/10.9734/BJMCS/2014/11563 - 15. Hafez, M.G., Kauser, M.A. and Akter, M.T. (2014) Some New Exact Traveling Wave Solutions of the Cubic Nonlinear Schrodinger Equation Using the -Expansion Method. International Journal of Science and Technology, 3, 848-851.
- 16. Hafez, M.G. and Akbar, M.A. (2015) New Exact Traveling Wave Solutions to the (1+1)-Dimensional Klein-Gordon-Zakharov Equation for Wave Propagation in Plasma Using the Exp(-Φ(ξ))-Expansion Method. Propulsion and Power Research, 4, 31-39.
http://dx.doi.org/10.1016/j.jppr.2015.02.002 - 17. Hafez, M.G., Alam, M.N. and Akbar, M.A. (2014) Application of the -Expansion Method to Find the Exact Solutions for the Solitary Wave Equation in Unmagnatized Dusty Plasma. World Applied Sciences Journal, 32, 2150-2155.
- 18. Hafez, M.G. and Alam, M.N. (2015) Exact Solutions for Some Important Nonlinear Physical Models, via (2+1) Dimensional Sine-Gordon Equation, (2+1) Dimensional Sinh-Gordon Equation, DBM Equation and TBD Equation. Asian Journal of Mathematics and Computer Research, 5, 157-174.
- 19. Hafez, M.G., Ali, M.Y., Chowdury, M.K.H. and Kauser, M.A. (2016) Application of the -Expansion Method for Solving Nonlinear TRLW and Gardner Equations. International Journal of Mathematics and Computation, 27, 44-56.
- 20. Wazwaz, A.M. (2004) A Sine-Cosine Method for Handle Nonlinear Wave Equations. Mathematical and Computer Modelling, 40, 499-508.
http://dx.doi.org/10.1016/j.mcm.2003.12.010 - 21. Jawad, A.J.M., Petkovic, M.D. and Biswas, A. (2010) Modified Simple Equation Method for Nonlinear Evolution Equations. Applied Mathematics and Computation, 217, 869-877.
http://dx.doi.org/10.1016/j.amc.2010.06.030 - 22. Hafez, M.G., Alam, M.N. and Akbar, M.A. (2014) Exact Travelling Wave Solutions to the Klein-Gordon Equation Using Novel (G’/G)-Expansion Method. Result in Physics, 4, 177-184.
http://dx.doi.org/10.1016/j.rinp.2014.09.001 - 23. Wang, M.L., Li, X.Z. and Zhang, J. (2008) The (G’/G)-Expansion Method and Traveling Wave Solutions of Nonlinear Evolution Equations in Mathematical Physics. Physics Letters A, 372, 417-423.
http://dx.doi.org/10.1016/j.physleta.2007.07.051 - 24. Taghizadeh, N. and Mirzazadeh, M. (2012) The Modified Extended Tanh Method with the Riccati Equation for Solving Nonlinear Partial Differential Equations. Mathematica Aeterna, 2, 145-153.
- 25. Hafez, M.G. and Akbar, M.A. (2015) An Exponential Expansion Method and Its Application to Strain Wave Equation in Microstructured Solids. Ain Shams Engineering Journal, 6, 683-690.
http://dx.doi.org/10.1016/j.asej.2014.11.011 - 26. Hafez, M.G. and Lu, D.C. (2015) Traveling Wave Solutions for Space-Time Fractional Nonlinear Evolution Equations.
http://arxiv.org/abs/1512.00715 - 27. Yuan, J.M. and Wu, J. (2010) A Dual-Petrov-Galerkin Method for Two Integrable Fifth-Order KdV Type Equations. Discrete and Continuous Dynamical Systems, 26, 1525-1536.
http://dx.doi.org/10.3934/dcds.2010.26.1525 - 28. Sawda, K. and Kotera, T. (1974) A Method Finding N-Soliton Solutions of the Kdv and KdV-Like Equations. Progress of Theoretical Physics, 51, 1355-1367.
http://dx.doi.org/10.1143/PTP.51.1355 - 29. Wazwaz, A.M. (2007) The Extended Tanh Method for New Solitons Solutions for Many Forms of the Fifth-Order KdV Equations. Applied Mathematics and Computation, 84, 1002-1014. http://dx.doi.org/10.1016/j.amc.2006.07.002
- 30. Gomez, C.A. and Salas, A. (2008) The Generalized Tanh-Coth Method to Special Types of the Fifth-Order KdV Equations. Applied Mathematics and Computation, 203, 873-880.
http://dx.doi.org/10.1016/j.amc.2008.05.105 - 31. Matinfar, H., Aminzadesh, M. and Nemati, M. (2014) Exp-Function Method for the Exact Solutions of Sawda-Kotera Equation. Indian Journal of Pure and Applied Mathematics, 45, 111-119.
http://dx.doi.org/10.1007/s13226-014-0054-y - 32. Goktas, U. and Hereman, W. (2008) Symbolic Computation of Conserved Densities for Systems of Nonlinear Evolution Equations. Journal of Symbolic Computation, 11, 1-31.
- 33. Kichenassamy, S. and Olver, P.J. (1991) Existence and Nonexistence of Solitary Wave Solutions to Higher-Order Model Evolution Equations. SIAM Journal on Mathematical Analysis, 23, 1141-1166.
http://dx.doi.org/10.1137/0523064 - 34. Olver, P.J. (1979) Euler Operations and Conservation Laws of the BBM Equations. Mathematical Proceedings of the Cambridge Philosophical Society, 85, 143-159.
http://dx.doi.org/10.1017/S0305004100055572
NOTES
*Corresponding author.











