Journal of Applied Mathematics and Physics
Vol.03 No.11(2015), Article ID:61233,5 pages
10.4236/jamp.2015.311166
Application of Focal Curves to the Evaluation of Conic Diffraction Lines
Stefan Enghardt, Jürgen Bauch
Institut für Werkstoffwissenschaft, TU Dresden, Dresden, Germany

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution-NonCommercial International License (CC BY-NC).
http://creativecommons.org/licenses/by-nc/4.0/



Received 18 September 2015; accepted 16 November 2015; published 19 November 2015
ABSTRACT
Micro diffraction methods like the Kossel or X-ray rotation tilt techniques generate diffraction patterns consisting of conic sections. Extracting information about lattice parameters, orientation or stresses from those patterns generally requires additional information. As a consequence, it is necessary to make high precision measurements of the pattern center and the detector-sample distance. By modeling the focal curves of a diffraction pattern it is possible to determine these parameters from only a single exposure. The focal curves of the conic sections in the detected image intersect (ideally) at the inspected sample point. This point is also the apex of all diffraction cones. The use of the geometry of the focal curves leads to an improved accuracy for the determination of lattice constants, residual stress and strain tensors by avoiding mechanical frames and their accompanying measurement errors. Therefore, by using this analysis route it is possible to extract three-dimensional crystal information out of a single two-dimensional diffraction pattern.
Keywords:
Micro Diffraction, Kossel, X-Ray Rotation Tilt Technique, EBSD, Single-Crystal

1. Introduction
In order to gather quantitative three-dimensional lattice information from two-dimensional diffraction patterns it is in most cases necessary to obtain additional three-dimensional information. This typically includes the detector-sample distance (cp. Kossel and Laue technique, X-ray-rotation tilt technique, diffractometers etc.). Measurement errors obtained when determining this distance directly influence the results or possibly lead to non- converging numerical results. In terms of the Kossel technique, the need to measure this parameter is a distinct disadvantage with regard to the automation of the whole procedure. An analysis option in which these measurements are avoided will therefore lead to faster and more accurate results. The most important tool needed to achieve this goal is the application of the so-called focal curves for diffraction patterns consisting of conic sections [1] . Sources discussing them are scarce since ca. 1950.
2. Focal Curves
If the sample does not lie in the detector plane then the diffraction cones (half opening angle is 90˚ minus Bragg angle) intersect with the detector in the form of an ellipse, hyperbola or parabola. This is the case for the Kossel technique, X-ray rotation tilt technique and EBSD. Each of the diffraction lines forms a pair with another conic section perpendicular to the detector plane (cp. Table 1). These additional curves are called focal curves since their vertices are the foci of the given conic sections. Correspondingly, their foci are the vertices of the given focal curves (cp. Figure 1 [2] ). Circular diffraction lines form a special case. If viewed as the limit of an ellipse,


Figure 1. Elliptic diffraction line (a); orthogonal plane (b); focal curve corresponding to the diffraction line (c) and overview of both curves (d).
Table 1. Comparison of focal curve pairs and their corresponding parameters.
the corresponding limit of the focal hyperbola coincides with a straight line perpendicular to the detector. This line does not form a (mathematically) well defined focal curve pair with the given circle. Therefore, this case may have to be treated separately.
Dupin’s theorem (of focal curves [1] ) implies: If there is a conic diffraction line on the detector, then the place where the diffraction occurred lies on the corresponding focal curve. By corollary, the associated lattice plane normal is the tangent to the focal curve in that sample point [3] .
If there are multiple reflections on the detector (and not all of them are concentric circles), then the point where all corresponding focal curves intersect is the sample point that was investigated. The foot of a dropped perpendicular to the detector plane is the photogrammetric pattern center. Since the focal curves are well defined by information from just the detector plane, additional 3D-information are no longer needed (that were e.g. gathered from shadows of steel balls in [4] , a mechanically sensible wire lattice, etc.). By completely avoiding these sources of error, more accurate values of the lattice parameters, orientations and stresses can be obtained. It also aids in the development of a widely automated evaluation method for Kossel and rotation tilt images.
3. Calculation of Sample Position
From an ideal geometric point of view all focal curves intersect at two points that are reflections of each other across the detector plane. It is sufficient to restrict calculations to the half space “above” the detector plane. Due to digitalization errors, line broadening and background noise there is no exact point of focal curve intersection. Thus numerical methods have to be employed to calculate the point closest to all focal curves. In order to avoid additional errors in the two step calculation (1. calculating parameters of the diffraction lines and 2. calculating “intersection” of focal curves) the following property can be employed:
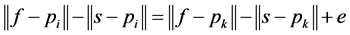 (1)
(1)
s… examined sample point
f… focal point of the given diffraction curve (in the case of an elliptic diffraction line f has to lie on the same focal curve arm as s)
pi, pk… different points of the given diffraction curve
e… error (ideally e = 0)
This follows from Dupin’s theorem [3] . By taking f and s as variables and using a sufficient number of points on the diffraction lines a solution can be found by using an appropriate non-linear least squares solver (e.g. Gauß-Newton). Equation (1) leads to the following residual function:
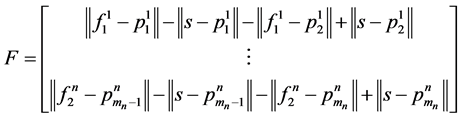 (2)
(2)
F in (2) takes in account both the foci of ellipse and hyperbola, and the points 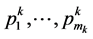 of the diffraction line k (k = 1, ∙∙∙, n). The starting values can be generated by principal axis transformation (for f) and measuring the sample position (for s). Alternatively, using a method which only relies on the detected image, the (start-) pattern center can be calculated by intersecting the principal axes of two diffraction lines (for sx and sy). The sample distance sz can then be calculated by intersecting the line through the pattern center that is perpendicular to the detector plane with one of the focal curves which was used to calculate the pattern center (cp. Figure 2).
of the diffraction line k (k = 1, ∙∙∙, n). The starting values can be generated by principal axis transformation (for f) and measuring the sample position (for s). Alternatively, using a method which only relies on the detected image, the (start-) pattern center can be calculated by intersecting the principal axes of two diffraction lines (for sx and sy). The sample distance sz can then be calculated by intersecting the line through the pattern center that is perpendicular to the detector plane with one of the focal curves which was used to calculate the pattern center (cp. Figure 2).
If a detected curve is approximately a circle (=both foci coincide) or a parabola (=one focus is at infinity) special care has to be taken in order to avoid issues related to computer precision. Although all reflections (generally Kα1, Kα2 and Kβ) can be used in the calculation to improve precision, the starting values should be calculated from reflections whose principal axis does not form a glancing intersection (or are identical). Thus diffraction lines belonging to lattice planes of different Miller indices should be used if possible.
The attainable precision is only limited by the capability of extracting maxima from the reflection fine structure and consequently the crystal quality and detector resolution.
4. Obtaining Crystal Parameters
If no restrictions upon the crystal structure are imposed, then at least six different reflections need to be visible on the detector in order to calculate all six lattice parameters (cp. Figure 3). Any additional information (e.g. a strictly biaxial stress tensor) may lower these requirements and, therefore, accelerate computational speed as
Figure 2. Scheme of the layout used to calculate a numerical starting position of the examined sample point from two conic reflections.
Figure 3. Kossel diffraction image of monocrystalline copper in proximity of the 002 pole showing multiple conic diffraction lines and their Laue indices (digitalized X-ray film, detector-sample distance approx. 300 mm).
well as improve precision.
Vectors from the calculated inspected sample position to the diffraction line points can now be determined. The diffraction cone axis (lattice plane normal) can be calculated as well (see Section 2). As a consequence the diffraction cone opening angle can be calculated which leads to the corresponding Bragg angle. Depending on the known precision of the utilized wavelength the spacing between the lattice planes corresponding to all visible reflections can be calculated using Bragg’s law. If utilized in the form of another regression model, the high accuracy of Section 2 can be retained. The error depends directly on the wavelength precision and indirectly on the image resolution and number of usable data points, and the number of visible lines.
5. Conclusions
Many micro diffraction techniques generate images containing sections of diffraction cones. Some of these, e.g. the Kossel technique, are limited in precision by the method employed to analyze the diffraction pattern itself. By utilizing the focal curves it is possible to avoid the use of imprecise measuring aids and to accelerate the evaluation of the detected image by avoiding the use of an additional data set (like measuring the shadows of the steel balls discussed in [4] ). This route raises the attainable precision from high quality patterns to that of the known wavelengths of the diffracted radiation. In the case of the Kossel technique this means further improvement in the calculation of high precision residual strain/stress tensors.
In addition to aiding the precision of various techniques the focal curves may also be a useful tool when automating parts of the evaluation process.
Acknowledgements
We are thankful for the financial support of the Deutsche Forschungsgemeinschaft. We also thank Dr. R. Boucher for his assistance.
Cite this paper
Stefan Enghardt,Jürgen Bauch, (2015) Application of Focal Curves to the Evaluation of Conic Diffraction Lines. Journal of Applied Mathematics and Physics,03,1386-1390. doi: 10.4236/jamp.2015.311166
References
- 1. Henschel, F. and Bauch, J. (2013) Application of Focal Curves for X-Ray Microdiffraction Methods. Journal for Geometry and Graphics, 17, 205-211.
- 2. Henschel, F., Enghardt, S. and Bauch, J. (2013) Neuartige Auswertung von Mikrobeugungsaufnahmen mittels Fokalkurven. Zeitschrift für Kristallographie Supplement, 33, 33-35.
http://dx.doi.org/10.1524/9783486858983.33 - 3. Kommerell, K. (1936) Das Grenzgebiet der elementaren und höheren Mathematik. K. F. Koehler Verlag, Leipzig.
- 4. Biggin, S. and Dingley, D.J. (1977) A General Method for Locating the X-Ray Source Point in Kossel Diffraction. Journal of Applied Crystallography, 10, 376-385.
http://dx.doi.org/10.1107/S0021889877013806




