Journal of Applied Mathematics and Physics
Vol.03 No.06(2015), Article ID:57406,14 pages
10.4236/jamp.2015.36078
Numerical Solution of MHD Boundary Layer Flow of Non-Newtonian Casson Fluid on a Moving Wedge with Heat and Mass Transfer and Induced Magnetic Field
Nabil T. El-Dabe1, Ahmed Y. Ghaly1, Raafat R. Rizkallah1, Karem M. Ewis2, Ameen S. Al-Bareda1*
1Department of Mathematics, Faculty of Education, Ain Shams University, Cairo, Egypt
2Department of Engineering Mathematics and Physics, Faculty of Engineering, El-Fayoum University, El-Fayoum, Egypt
Email: *ameen_azeez@hotmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 May 2015; accepted 21 June 2015; published 25 June 2015
ABSTRACT
The paper investigates the numerical solution of the magnetohydrodynamics (MHD) boundary layer flow of non-Newtonian Casson fluid on a moving wedge with heat and mass transfer. The effects of thermal diffusion and diffusion thermo with induced magnetic field are taken in consideration. The governing partial differential equations are transformed into nonlinear ordinary differential equations by applying the similarity transformation and solved numerically by using finite difference method (FDM). The effects of various governing parameters, on the velocity, temperature and concentration are displayed through graphs and discussed numerically. In order to verify the accuracy of the present results, we have compared these results with the analytical solutions by using the differential transform method (DTM). It is observed that this approximate numerical solution is in good agreement with the analytical solution. Furthermore, comparisons of the pre- sent results with previously published work show that the present results have high accuracy.
Keywords:
Casson Fluid, Induced Magnetic Field, Boundary Layer, Moving Wedge, Radiation, Soret and Dufour Effects

1. Introduction
The induced magnetic field is arisen due to a strong magnetic field. The problems with induced magnetic field play an important role in a number of industrial applications such as fiber or granular insulation, liquid-metals, electrolytes, ionized gases as well as the geothermal systems. The study of the boundary layer flow under the influence of a magnetic field with the induced magnetic field was considered by a few authors. For example, Raptis and Perdikis [1] studied the MHD free convection boundary layer flow past an infinite vertical porous plate. Very little attention has been paid to the boundary layer flow and heat transfer taking the effect of the induced magnetic field and thermal radiation into consideration. For example, Kumari et al. [2] considered the MHD flow and heat transfer over a stretching surface by considering the effect of the induced magnetic field. On the other hand, Takhar et al. [3] investigated the unsteady free convection flow at the stagnation point in the presence of a magnetic field. Recently Ali et al. [4] studied MHD stagnation-point flow and heat transfer towards stretching sheet with induced magnetic field. Khamisah Jafar et al. [5] studied viscous dissipation and radiation effects in MHD stagnation point flow towards a stretching sheet with induced magnetic field. The thermal reversal in MHD stagnation point flow towards a stretching sheet with induced magnetic field and viscous dissipation effects have been investigated by Kashif Ali and Muhammad Ashraf [6] . The MHD mixed convection boundary layer flow toward a stagnation point on a vertical surface with induced magnetic field was studied by Ali et al. [7] . Khamisah Jafar et al. [8] discussed the MHD boundary layer flow due to a moving wedge in a parallel stream with the induced magnetic field.
The analysis of non-Newtonian fluids has many applications in industrials such as ground water hydrology, petroleum reservoir, nuclear waste disposal, geothermal energy production, transpiration cooling, design of solid matrix heat exchange and paced bed chemical catalytic reactors. Also, there are some models of non-Newtonian fluids such as Casson model which concerned one of the most important applications of theoretical fluid mechanics to problems arising in physiology, mainly in describing the flow of the blood. Casson [9] proposed a model to describe the flow curves of suspensions of pigments in lithographic varnishes used for the preparation of printing inks. Eldabe et al. studied some problems of non-Newtonian fluids such as ( [10] - [14] ).
In the present work, we extend and generalize the work of [8] to include the boundary layer motion of non- Newtonian fluid obeying Casson model with heat and mass transfer in the presence of radiation and mixed diffusion. The main objective of the present work is to obtain the numerical solutions of the MHD boundary layer flow of Casson fluid on a moving wedge with heat and mass transfer. The effects of thermal diffusion and diffusion thermo with induced magnetic field are taken into consideration. The governing equations of motion with the boundary conditions are solved numerically by using (FDM) and analytically by using (DTM). The solutions are obtained as a function of the physical parameters of the problem; then the effects of these various parameters of the problem on these solutions have been computed and discussed in detail and illustrated through some figures. The special cases of our problem are compared with the previous published works. This showed that there is a good agreement between them.
2. Mathematical Formulation
Let us consider a steady, laminar, hydromagnetic coupled heat and mass transfer by mixed convection flow on a wedge plate in a parallel free stream with a variable induced magnetic field applied parallel to the wedge walls outside the boundary layer. The equations governing the steady motion of an incompressible non-Newtonian electrically conducting fluid in presence of a magnetic field are:
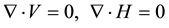 (1)
(1)
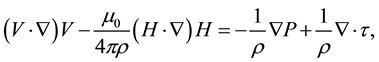 (2)
(2)
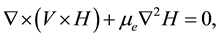 (3)
(3)
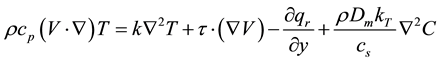 (4)
(4)
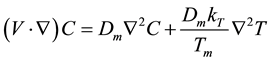 (5)
(5)
where V is the fluid velocity vector, H is the induced magnetic field vector,
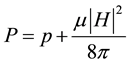 is the magnetohy-
is the magnetohy-
drodynamic pressure, p is the fluid pressure,
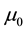 is the magnetic permeability,
is the magnetic permeability,
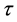 is the stress tensor,
is the stress tensor,
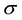 is the electrical conductivity, T is the temperature, k is the thermal conductivity,
is the electrical conductivity, T is the temperature, k is the thermal conductivity,
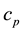 is the specific heat at constant
is the specific heat at constant
pressure,
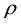 is the density of the fluid,
is the density of the fluid,
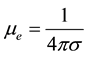 is the magnetic diffusivity,
is the magnetic diffusivity,
 is the radiative heat flux, C
is the radiative heat flux, C
is the species concentration,
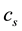 is the concentration susceptibility,
is the concentration susceptibility,
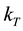 is thermal diffusion ratio,
is thermal diffusion ratio,
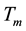 is mean fluid temperature and
is mean fluid temperature and

The rheological equation of state for an isotropic flow of a Casson fluid can be expressed as [9] :

In the above equation







We take the Cartesian coordinates x measured along the surface of the wedge and y normal to it, respectively. If








The boundary conditions are as follows:

where





We assume here that







By using the Rosseland approximation, the radiative heat flux


where





In view of Equations (14) and (15), Equation (11) reduces to

3. Method of Solutions
To solve system of Equations (7)-(13), we will consider the following similarity transformations:

where





tration. Further,






By using Equation (17) in the Equations (9)-(12) and Equation (16), we get the following ordinary differential equations in dimensionless form




where









Also, the subjected boundary conditions Equation (13) will now take the form:

where

3.1. The Differential Transform Method (DTM)
The differential transformation of an analytical function


where




Combining Equations (23) and (24), we obtain

From Equations (23)-(25), it can be seen that the differential transformation method is derived from Taylor’s series expansion, but the method does not calculate the derivatives representatively. However, the relative derivatives are calculated by an iterative way which is described by the transformed equations of the original function. For implementation purposes, the function


By Equation (23), the following theorems can be deduced:
Theorem 3.1.1 If

Theorem 3.1.2 If

Theorem 3.1.3 If

Theorem 3.1.4 If

Theorem 3.1.5 If

Theorem 3.1.6 If

Theorem 3.1.7 If

3.2. Basic Concepts of the Multi-Step Differential Transform Method (MDTM)
When the DTM is used for solving differential equations with the boundary condition at infinity or problems that have highly non-linear behavior, the obtained results were found to be incorrect (when the boundary-layer variable go to infinity, the obtained series solutions are divergent). Besides that, power series are not useful for large values of the independent variable.
To overcome this shortcoming, the MDTM that has been developed for the analytical solution of the differential equations is presented in this section. For this purpose, the following non-linear initial-value problem is considered:

subject to the initial conditions

Let [0, T] be the interval over which we want to find the solution of the initial-value problem (27). In actual applications of the DTM, the approximate solution of the initial value problem (27) can be expressed by the following finite series:

The multi-step approach introduces a new idea for constructing the approximate solution. Assume that the interval [0, T] is divided into M subintervals



using the initial conditions




in Equation (23) is replaced by



where

The new algorithm, MDTM, is simple for computational performance for all values of h. It is easily observed that if the step size h = T, then the MDTM reduces to the classical DTM. As we will see in the next section, the main advantage of the new algorithm is that the obtained series solution converges for wide time regions and can approximate non-chaotic or chaotic solutions.
3.3. Analytical Solution Be the MDTM
By applying the MDTM to Equations (18)-(21), gives the following recursive relations in each sub-domain





where

The differential transformed boundary conditions in Equation (22) to:

where



The velocity, induced magnetic field, temperature and concentration distributes achieved with the aid of MATHAMATICA application software.
3.4. Numerical Solutions by Using the FDM
To solve the ordinary differential Equations (18)-(21), we use a finite difference based numerical algorithm. We reduce the order of Equations (18) and (19) by one with the help of the substitution:

Equations (18)-(21) in view of Equation (37) can be written as:




The boundary conditions:

Now, we can write Equations (37)-(41) in the following finite difference form




The velocity, induced magnetic field, temperature and concentration distributes at all interior nodal points computed by successive applications of the above finite difference equations and these are achieved with the aid of MATLAB application software.
4. Results and Discussion
The system of the equations which describe the motion of Casson fluid in the boundary layer with heat and mass transfer and in the presence of induced magnetic field with radiation are solved analytically by using (DTM) and numerically by using (FDM). The values of the velocity, temperature, concentration and induced magnetic field are obtained as a functions of the physical parameters of the problem such as Casson parameter


Figures 1-5 represent the velocity profiles for the flow parameters. The effect of











Figure 1. Velocity profiles


Figure 2. Velocity profiles


Figure 3. Velocity profiles

Figure 4. Velocity profiles

Figure 5. Velocity profiles


Figure 6. Induced magnetic profiles


Figure 7. Induced magnetic profiles


Figure 8. Induced magnetic profiles

Figure 9. Induced magnetic profiles


Figure 10. Induced magnetic profiles


Figure 11. Temperature profiles


Figure 12. Temperature profiles


Figure 13. Temperature profiles


Figure 14. Temperature profiles

Figure 15. Temperature profiles


Figure 16. Concentration profiles


Figure 17. Concentration profiles


Figure 18. Concentration profiles


In order to verify the accuracy of the numerical solution of present work by using (FDM) we have compared these results for


Table 1. Comparison between the previous obtained values of

Table 2. Comparison between the previous obtained values of

Table 3. Comparison between the previous obtained values of

Table 4. Comparison between the previous obtained values of

5. Conclusions
In this work we have obtained the numerical solution of MHD boundary layer flow of non-Newtonian Casson fluid on a moving wedge with heat and mass transfer and induced magnetic field. The effects of thermal diffusion and diffusion thermo with induced magnetic field are taken into consideration. The resulting partial differential equations which describe the problem are transformed into ordinary differential equations by using a similarity transformation and then solved numerically by using the finite difference method (FDM) and analytically by using (DTM). A representative set of numerical results for velocity, induced magnetic field, temperature and concentration profiles is presented graphically and discussed. The figures and tables clearly show that the results by using (FDM) are in excellent agreement with previously published works and with the results of the analytical solution by using (DTM). The important results for this study summarized as follows:
The velocity distribution decreases with the increase of

The temperature distribution increases with the increase of Ra, E and Du, while it decreases with the increases of Pr and
The induced magnetic field distribution increases with the increase of

The concentration distribution increases with increase of S0, while it decreases with the increases of Sc and
References
- Raptis, A. and Perdikis, C. (1984) Free Convection under the Influence of a Magnetic Field. Nonlinear Analysis: Theory, Methods & Applications, 8, 749-756.
- Kumari, M., Takhar, H.S. and Nath, G. (1990) MHD Flow and Heat Transfer over a Stretching Surface with Prescribed Wall Temperature or Heat Flux. Wärme - und Stoffübertragung, 25, 331-336.
- Takhar, H.S., Kumari, M. and Nath, G.G. (1993) Unsteady Free Convection Flow under the Influence of a Magnetic Field. Archive of Applied Mechanics, 63, 313-321. http://dx.doi.org/10.1007/BF00793897
- Ali, F.M. Nazar, R., Arifin, N.M. and Pop, I. (2011) MHD Stagnation-Point Flow and Heat Transfer towards Stretching Sheet with Induced Magnetic Field. Applied Mathematics and Mechanics, 32, 409-418.
- Ali, K., Ashraf, M., Ahmad, S. and Batool, K. (2012) Viscous Dissipation and Radiation Effects in MHD Stagnation Point Flow towards a Stretching Sheet with Induced Magnetic Field. World Applied Sciences Journal, 16, 1638-1648.
- Ali, K. and Ashraf, M. (2012) Thermal Reversal in MHD Stagnation Point Flow towards a Stretching Sheet with Induced Magnetic Field and Viscous Dissipation Effects. World Applied Sciences Journal, 16, 1615-1625.
- Ali, F.M., Nazar, R., Arifin, N.M. and Pop, I. (2011) MHD mixed Convection Boundary Layer Flow toward a Stagnation Point on a Vertical Surface with Induced Magnetic Field Was Studied. Journal of Heat Transfer, 133, Article ID: 022502, 1-6.
- Jafar, K., Nazar, R., Ishak, A. and Pop, I. (2013) MHD Boundary Layer Flow Due to a Moving Wedge in a Parallel Stream with the Induced Magnetic Field. J. Boundary Value Problems, 1-14.
- Nakayama, M. and Sawada, T. (1988) Numerical Study on the Flow of a Non-Newtonian Fluid through an Axisymmetric Stenosis. Journal of Biomechanical Engineering, 110, 137-143. http://dx.doi.org/10.1115/1.3108418
- Abdelnaby, M.A., Eldabe, N.T. and Abou-zeid, M.Y. (2006) Numerical Study of Pulsatile MHD Non-Newtonian Fluid Flow With heat and Mass Transfer through a Porous Medium between Two Permeable Parallel Plates. Ind. J. Mech. Cont. & Math Sci, 1, 1-15.
- Eldabe, N.T., El-Sakka, A.G. and Fouda, A. (2002) Numerical Treatment of the MHD Convective Heat and Mass Transfer in an Electrically Conducting Fluid over an Infinite Solid Surface in Presence of Internal Heat Generation. Zeitschrift für Naturforschung, 58, 601-611.
- Eldabe, N.T., El-Sayed, M.F., Ghaly, A.Y. and Sayed, H.M. (2007) Peristaltically Induced Transport of a MHD Biviscosity Fluid in a Non-Uniform Tube. Physica A: Statistical Mechanics and its Applications, 383, 253-266. http://dx.doi.org/10.1016/j.physa.2007.05.027
- Eldabe, N.T., El-Sayed, M.F., Ghaly, A.Y. and Sayed, H.M. (2008) Mixed Convective Heat and Mass Transfer in a Non-Newtonian Fluid at a Peristaltic Surface with Temperature-Dependent Viscosity. Archive of Applied Mechanics, 78, 599-624. http://dx.doi.org/10.1007/s00419-007-0181-6
- Eldabe, N.T. and Hassan, A.A. (1991) Non-Newtonian-Flow Formation in Couette Motion in Magnethohydrodynamics with Time-Varying Suction. Canadian Journal of Physics, 69, 75-85. http://dx.doi.org/10.1139/p91-012
- Zhou, J.K. (1986) Differential Transformation and Its Application for Electrical Circuits. Huazhong University Press, Wuhan.
- Rajagopal, K.R., Gupta, A.S. and Nath, T.Y. (1983) A Note on the Falkner-Skan Flows of a Non-Newtonian Fluid. International Journal of Non-Linear Mechanics, 18, 313-320. http://dx.doi.org/10.1016/0020-7462(83)90028-8
- Kuo, B.L. (2003) Application of the Differential Transformation Method to the Solutions of Falkner-Skan Wedge Flow. Acta Mechanica, 164, 161-174. http://dx.doi.org/10.1007/s00707-003-0019-4
- Ishak, A., Nazar, R. and Pop, I. (2009) MHD Boundary Layer Flow past a Moving Wedge. Magnetohydrodynamics, 45, 3-10.
NOTES
*Corresponding author.


































