Journal of Applied Mathematics and Physics
Vol.03 No.05(2015), Article ID:56224,7 pages
10.4236/jamp.2015.35061
Existence of Viscosity Solutions to a Parabolic Inhomogeneous Equation Associated with Infinity Laplacian
Fang Liu
Department of Applied Mathematics, School of Science, Nanjing University of Science & Technology, Nanjing, China
Email: sdqdlf78@126.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 February 2015; accepted 5 May 2015; published 11 May 2015
ABSTRACT
In this paper, we obtain the existence result of viscosity solutions to the initial and boundary value problem for a nonlinear degenerate parabolic inhomogeneous equation of the form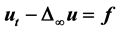 , where
, where 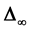 denotes infinity Laplacian given by
denotes infinity Laplacian given by .
.
Keywords:
Infinity Laplacian, Viscosity Solution, Inhomogeneous Equation

1. Introduction
In this paper, we consider the nonlinear degenerate parabolic inhomogeneous equation involving infinity La- place
 , (1)
, (1)
where
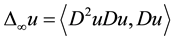
denotes the 3-homogeneous infinity Laplacian. We want to establish the existence result of viscosity solutions to the initial and Dirichlet boundary problem.
The homogeneous infinity Laplace equation 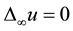 is the Euler-Lagrange equation associated with
is the Euler-Lagrange equation associated with 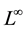 - variational problem. See for details [1] -[5] and the references therein. Recently, Juutinen and Kawohl [6] con- sidered the degenerate and singular parabolic equation
- variational problem. See for details [1] -[5] and the references therein. Recently, Juutinen and Kawohl [6] con- sidered the degenerate and singular parabolic equation
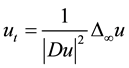 . (2)
. (2)
They proved the existence and uniqueness for both Dirichlet and Cauchy problems, established interior and boundary Lipschitz estimates and a Harnack inequality, and also provided numerous explicit solutions. Due to the degeneracy and the singularity of the Equation (2), they introduced the approximating equations to obtain the existence result with the aid of the uniform continuity estimates. And in [7] we considered the corresponding inhomogeneous parabolic equation. Notice that the 1-homogeneous infinity Laplacian
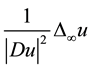 (3)
(3)
is related to game theory named tug-of-war [8] . In [9] -[12] , Akagi, Suzuki, et al. considered the following degenerate parabolic equation
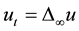 .
.
They also introduced the corresponding approximating equations and got the uniform continuity estimates of approximate solutions by the barrier function arguments. By this approximate procedure, the existence of the solutions was obtained. They also proved the uniqueness and the asymptotic behavior of the viscosity solutions. In [13] , Portilheiro and Vázquez considered the parabolic equation
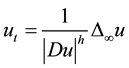 ,
,
with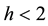 . They proved existence and uniqueness of viscosity solutions and derived the asymptotic behavior of the solutions for the Cauchy problem and the initial and Dirichlet problem with zero boundary conditions. In [14] , Portilheiro and Vázquez studied the nonlinear porous medium type equation involving the infinity Laplacian operator
. They proved existence and uniqueness of viscosity solutions and derived the asymptotic behavior of the solutions for the Cauchy problem and the initial and Dirichlet problem with zero boundary conditions. In [14] , Portilheiro and Vázquez studied the nonlinear porous medium type equation involving the infinity Laplacian operator
 . (4)
. (4)
By the density-to-pressure transformation, they transformed the Equation (4) into a new equation, then the existence, uniqueness and asymptotic behavior etc. were obtained.
In this article, we are interested in the parabolic version of the infinity Laplacian here. We think that Equation (1) is interesting, because it not only is degenerate, but also has many applications in image processing and optimal transportation etc. The parabolic equation involving infinity Laplacian operator has received a lot of attention in the last decade, notably due to its application to image processing, the main usage being in the reconstructions of damaged digital images [15] . For numerical purposes it has been necessary to consider also the evolution equation corresponding to the infinity Laplace operator. We prove the existence of viscosity solu- tions to the initial-Dirichlet problem by approximating procedure. The approximation process is introduced in [6] for the infinity Laplacian evolution and followed in [9] [13] [14] etc.
This paper is organized in the following order. In Section 2, we give the notations, definitions of viscosity solutions related to the Equation (1). In Section 3, we prove our main existence result by approximating pro- cedure.
2. Preliminaries
Throughout of this paper, we use the following notation: If ,
, 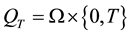 ,
, 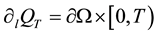 denotes the lateral bouncary,
denotes the lateral bouncary, 







In the following paper, we adopt the definition of viscosity solutions, (see for example [16] ).
Definition 2.1. Suppose that 









then we say that 
Similarly, 





then we say that 
If 

3. Existence Theorem
In this section we will prove the existence of viscosity solutions to (1) with the initial and boundary data
Theorem 3.1. Let








in 
We use the approximate procedure, cf, [6] [9] [14] . We consider the approximating equations

where

with





Theorem 3.2. (Boundary regularity at






Then there exists a constant 





Moreover, if 










Proof. Step 1. Suppose first that 

where 
if

Clearly, 




if


Thus, by the classical comparison principle, we obtain
for every

we obtain the symmetric inequality, and hence the Lipschitz estimate

for 

Step 2. Suppose now that 


a point 


It is easy to check that 

Thus if 





where 



with this inequality it is straightforward to complete the proof. □
The full Lipschitz estimate in time now follows easily with the aid of the comparison principle and the fact that the Equation (7) is translation invariant.
Corollary 3.3. (Lipschitz regularity in time) If 



Theorem 3.2, then there exists a constant 




for all 







Proof. Let


and hence if
by the classical comparison principle and Theorem 3.2. This implies the Lipschitz estimate asserted above, and the proof for the case when 
Theorem 3.4. (Hölder regularity at the lateral boundary) Let





Then for each









for all 

Proof. Step 1. For every 


where

If 


Therefore

if
We have shown that 
Step 2. Let




provided 

Case 2. If




provided
Step 3. To prove 

Case 1. If


if 

Case 2. If

if
Step 4. In conclusion, we have shown that 



Therefore, we have 

for

we get the symmetric inequality. This finishes the proof. □
Due to the translation invariant of the equation and the comparison principle, we can extend the Hölder estimate to the interior of the domain, cf. [6] [14] etc.
Corollary 3.5. (Hölder regularity in space) Let





Then there exists









for all
Proof. Step 1. For fixed



By Theorem 3.4 we have that 









Step 2. When

This finishes the proof. □
The following theorem shows that one can obtain the Lipschitz estimate when one remove the Laplacian term from the equation, cf. [6] .
Theorem 3.1 follows now easily from Theorem 3.2 and 3.3 and the stability properties of viscosity solutions.
Proof. (Proof of Theorem 3.1) If 

Corollaries 3.3 and 3.5 and the comparison principle imply that the family of functions 



The existence for a general continuous data 
Acknowledgements
The author would like to thank the anonymous referee for some valuable suggestions.
Support
This work is supported by the National Natural Science Foundation of China, No.11171153.
References
- Aronsson, G. (1965) Minimization Problems for the Functional
. Arkiv för Matematik, 6, 33- 53. >http://html.scirp.org/file/4-1720263x266.png" class="200" />. Arkiv för Matematik, 6, 33- 53. http://dx.doi.org/10.1007/BF02591326
- Aronsson, G. (1966) Minimization Problems for the Functional
. II. Arkiv för Matematik, 6, 409-431.>http://html.scirp.org/file/4-1720263x267.png" class="200" />. II. Arkiv för Matematik, 6, 409-431.
- Crandall, M.G., Evans, L.C. and Gariepy, R.F. (2001) Optimal Lipschitz Extensions and the Infinity Laplacian. Calculus of Variations and Partial Differential Equations, 13, 123-139.
- Jensen, R. (1993) Uniqueness of Lipschitz Extensions: Minimizing the Sup Norm of the Gradient. Archive for Rational Mechanics and Analysis, 123, 51-74. http://dx.doi.org/10.1007/BF00386368
- Aronsson, G., Crandall, M. and Juutinen, P. (2004) A Tour of the Theory of Absolute Minimizing Functions. Bulletin of the AMS, 41, 439-505. http://dx.doi.org/10.1090/S0273-0979-04-01035-3
- Juutinen, P. and Kawohl, B. (2006) On the Evolution Governed by the Infinity Laplacian. Mathematische Annalen, 335, 819-851. http://dx.doi.org/10.1007/s00208-006-0766-3
- Liu, F. and Yang, X.P. (2015) Viscosity Solutions to a Parabolic Inhomogeneous Equation Associated with Infinity Laplacian. Acta Mathematica Sinica, English Series, 31, 255-271. http://dx.doi.org/10.1007/s10114-015-3244-6
- Peres, Y., Schramm, O., Sheffield, S. and Wilson, D. (2009) Tug of War and the Infinity Laplacian. Journal of the American Mathematical Society, 22, 167-210. http://dx.doi.org/10.1090/S0894-0347-08-00606-1
- Akagi, G. and Suzuki, K. (2007) On a Certain Degenerate Parabolic Equation Associated with the Infinity-Laplacian. Discrete and Continuous Dynamical Systems, Supplement, 18-27.
- Akagi, G. and Suzuki, K. (2008) Existence and uniqueness of viscosity solutions for a degenerate parabolic equation associated with the infinity-Laplacian. Calculus of Variations and Partial Differential Equations, 31, 457-471. http://dx.doi.org/10.1007/s00526-007-0117-6
- Akagi, G., Juutinen, P. and Kajikiya, R. (2009) Asymptotic Behavior of Viscosity Solutions for a Degenerate Parabolic Equation Associated with the Infinity-Laplacian. Mathematische Annalen, 343, 921-953. http://dx.doi.org/10.1007/s00208-008-0297-1
- Laurencot, P. and Stinner, C. (2010) Refined Asymptotics for the Infinite Heat Equation with Homogeneous Dirichlet Boundary Conditions. Communications in Partial Differential Equations, 36, 532-546. http://dx.doi.org/10.1080/03605302.2010.498493
- Portilheiro, M. and Vázquez, J.L. (2012) Degenerate Homogeneous Parabolic Equations Associated with the Infinity- Laplacian. Calculus of Variations and Partial Differential Equations, 31, 457-471. http://dx.doi.org/10.1007/s00526-012-0500-9
- Portilheiro, M. and Vázquez, J.L. (2012) A Porous Medium Equation Involving the Infinity-Laplacian, Viscosity Solutions and Asymptotic Behaviour. Communications in Partial Differential Equations, 37, 753-793. http://dx.doi.org/10.1080/03605302.2012.662665
- Caselles, V., Morel, J.M. and Sbert, C. (1998) An Axiomatic Approach to Image Interpolation. IEEE Transactions on Image Processing, 7, 376-386. http://dx.doi.org/10.1109/83.661188
- Crandall, M.G., Ishii, H. and Lions, P.L. (1992) User’s Guide to Viscosity Solutions of Second-Order Partial Differential Equations. Bulletin of the AMS, 27, 1-67. http://dx.doi.org/10.1090/S0273-0979-1992-00266-5
- Ladyženskaya, O.A., Solonnikov, V.A. and Ural’ceva, N.N. (1967) Linear and Quasilinear Equations of Parabolic Type, Translations of Mathematical Monographs, Vol. 23, American Mathematical Society, Providence, R.I.


















 . Arkiv för Matematik, 6, 33- 53. >http://html.scirp.org/file/4-1720263x266.png" class="200" />. Arkiv för Matematik, 6, 33- 53.
. Arkiv för Matematik, 6, 33- 53. >http://html.scirp.org/file/4-1720263x266.png" class="200" />. Arkiv för Matematik, 6, 33- 53.  . II. Arkiv för Matematik, 6, 409-431.>http://html.scirp.org/file/4-1720263x267.png" class="200" />. II. Arkiv för Matematik, 6, 409-431.
. II. Arkiv för Matematik, 6, 409-431.>http://html.scirp.org/file/4-1720263x267.png" class="200" />. II. Arkiv för Matematik, 6, 409-431.