Journal of Applied Mathematics and Physics
Vol.03 No.03(2015), Article ID:54909,11 pages
10.4236/jamp.2015.33044
Dynamical System of Three Magnetic Layers in the Presence of Porous Media
Sameh A. Alkharashi1,2
1Quesna Technical College, Tanta Technical Commercial Institute, Ministry of Higher Education, Cairo, Egypt
2Applied Sciences Department, College of Technological Studies, The Public Authority for Applied Education and Training (PAAET), Adiliya, Kuwait
Email: sameh7977@yahoo.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 January 2015; accepted 5 February 2015; published 23 March 2015
ABSTRACT
This paper concerns the linear stability of three viscous fluid layers in porous media. The system is composed of a middle fluid embedded between two semi-infinite fluids, in which the effect of the normal magnetic field is to introduce. The principle aim of this work is to investigate the influence of fluid viscosity and the porosity effect on the growth rate in the presence of normal magnetic field. The parameters governing the layers flow system, the magnetic properties and porosity effects strongly influence the wave forms and their amplitudes and hence the stability of the fluid. The stability criteria are discussed theoretically and numerically and stability diagrams are obtained, where regions of stability and instability are identified. It is found that the stabilizing role for the magnetic field is retarded when the flow is in porous media. Moreover, the increase in the values of permeability parameters plays a dual role, in stability behavior. It has been found that the phenomenon of the dual (to be either stabilizing or destabilizing) role is found for increasing the permeability parameter. It is established that both the viscosity coefficient and the magnetic permeability damps the growth rate, introducing stabilizing influence. The role of the magnetic field and Reynolds number is to increase the amplitude of the disturbance leading to the destabilization state of the flow system, promote the oscillatory behavior. Influence of the various parameters of the problem on the interface stability is thoroughly discussed.
Keywords:
Viscous Fluids, Magnetic Field, Three Layers Stability, Porous Media

1. Introduction
There has been a great deal of interest in magnetic fluids of the stability of hydrodynamic stability. A magnetic fluid, also known in the literature as a ferromagnetic fluid or simply a ferrofluid. In many previous researches has shown the importance of studying the hydrodynamic stability problems, for example capillary-gravity waves of permanent form at the interface between two unbounded magnetic fluids in porous media are investigated in paper [1] . In which the system is influenced by the horizontal direction of the magnetic field to the separation face of two semi-infinite homogeneous and incompressible fluids. It is found that the stabilizing role for the magnetic field is retarded when the flow is in porous media. In paper [2] the influence of viscosity on the stability of the plane interface separating two incompressible superposed fluids of uniform densities, when the whole system is immersed in a uniform horizontal magnetic field, has been studied. The authors in the research [3] have carried out the instability of viscous potential flow in a horizontal rectangular channel. The analysis leads to an explicit dispersion relation in which the effects of surface tension and viscosity on the normal stress are not neglected but the effect of shear stresses is. The unsteady electrohydrodynamic stability has been investigated by Elhefnawy [4] , where the stability analysis has been made of a basic flow of streaming fluids in the presence of an oblique periodic electric field. A series of studies for hydrodynamics stability have also been initiated by Drazin and Reid [5] and Joseph [6] .
The authors in paper [7] have investigated the stability properties of time periodically streaming superposed magnetic fluids through porous media under the influence of an oblique alternating magnetic field. Also, Zakaria et al. [8] have analyzed the effect of an externally applied electric field on the stability of a thin fluid film over an inclined porous plane, using linear and non-linear stability analysis in the long wave limit. Wray et al. [9] have investigate the evolution and stability of a wetting viscous fluid layer flowing down the surface of a cylinder, and surrounded by a conductive gas. Liu et al. [10] have studied the instability properties of two-dimensional non- Newtonian liquid sheets moving in an inviscid gaseous environment.
Based on a modified Darcy’s law for a viscoelastic fluid, Sirwah [11] has discussed the linear stability analysis of the electrified surface separating two coaxial Oldroyd-B fluid layers confined between two impermeable rigid cylinders in the presence of both interfacial insoluble surfactant and surface charge through porous media. Also, Tan and Masuoka [12] have extended Stokes? first problem to that for an Oldroyd-B fluid in a porous half space, where an exact solution was obtained by using Fourier sine transform. Zakaria [13] has investigated the time evolution of superposed layers of fluid flowing down inside an inclined permeable channel. Using the Kármán-Pohlhausen approximation, the problem is reduced to the study of the evolution equation for the liquid? liquid interface of the liquids film derived through a long wave approximation. Khan et al. [14] have demonstrated the analytical solutions for the magnetohydrodynamic flow of an Oldroyd-B fluid through a porous medium. They obtained the expressions for the velocity field and the tangential stress by means of the Fourier sine transform. Kumar and Singh [15] have investigated the stability of a plane interface separating two viscoelastic (Rivlin-Ericksen) superposed fluids in the presence of suspended particles.
In the present work we wish to consider an investigation of stability for flow in a porous medium under the effect of a magnetic field that is normal to the interface between the fluids. The considered system is composed of a viscous fluid layer of finite thickness embedded between two semi-infinite fluids. We have concentrated in this work to investigate the mechanisms of stability of three porous layers of fluids in the presence of normal magnetic field. This paper is organized as follows: This section has presented the motivation for the investigation in addition to relevant background information. In next section, we will give a formulation of the problem statement, including the basic equations of the fluid mechanics and Maxwell’s equations governing the motion of our model. In the third section and its subsections, are concerned with the derivation of the characteristic equation and numerical estimations for stability configuration. The salient results of our analysis are discussed and some important conclusions are drawn in final section of this paper.
2. Formulation of the Problem
The system under consideration is composed of an infinite horizontal viscous fluid sheet of vertical height 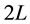 confined between two semi-infinite superposed incompressible viscous fluids. The fluids are considered to be influenced by the gravity force in the negative y-direction. The x-axis of the co-ordinate system is parallel to the direction of the fluid sheet flow, and the y-axis is normal to the fluid sheet with its origin located at the middle plane of the fluid sheet as shown in Figure 1. The superscripts (1), (2) and (3) refer to the lower fluid, middle sheet and upper fluid respectively, where
confined between two semi-infinite superposed incompressible viscous fluids. The fluids are considered to be influenced by the gravity force in the negative y-direction. The x-axis of the co-ordinate system is parallel to the direction of the fluid sheet flow, and the y-axis is normal to the fluid sheet with its origin located at the middle plane of the fluid sheet as shown in Figure 1. The superscripts (1), (2) and (3) refer to the lower fluid, middle sheet and upper fluid respectively, where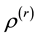 ,
, 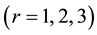 is the fluid densities,
is the fluid densities, 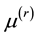 is the magnetic permeability and
is the magnetic permeability and  represents the viscosities of the fluids. The fluids are subjected to external magnetic field
represents the viscosities of the fluids. The fluids are subjected to external magnetic field
Figure 1. Sketch for the system under consideration. The y-axis is taken vertically upwards, the x-axis is taken horizontally at the half of the middle sheet.
acting in the positive y-direction. The two interfaces are parallel and the flow in each phase is every where parallel to each other. The surface deflections are expressed by 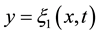 at
at 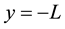 and
and  at
at , where at the initial state of the system, we assume that the fluid phases are viscous and have a common flat interfaces at
, where at the initial state of the system, we assume that the fluid phases are viscous and have a common flat interfaces at 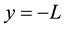 and
and .
.
2.1. Scaling Variables for the Evolution Equations
First, we will use the dimensionless variables to provide improved insight into the physics and in order to understand hydrodynamic stability better. So we define the corresponding dimensionless variables using the half thickness of the middle fluid sheet L as a length scale. Thus the stream velocity and the time are made dimensionless using 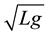 and
and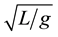 , while the applied magnetic field and the magnetic potential are made dimen-
, while the applied magnetic field and the magnetic potential are made dimen-
sionless by 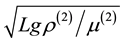 and
and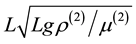 , respectively. In addition the viscosity
, respectively. In addition the viscosity
sure








The dynamics of the problem are described by the simultaneous solution of three field equations: Maxwell’s equations, Navier-Stokes equation, and the continuity equation. Assuming a quiescent initial state, therefore the base state velocity in the fluid layers is zero in which the flow is steady and fully developed. Fluid flow through a porous medium is often given by the phenomenological Darcy’s equation. Thus, the equations governing two- dimensional motion of a viscous incompressible fluid through porous medium are [3] -[7]

and the equation of continuity will be

where 

meability parameter and 

zontal gradient operator.
In writing Maxwell’s equations for the problem, we supposed that the electro-quasi-static approximation is valid for the problem, and hence the magnetic field equations read

Here, 



and thus we have the Laplace equation in the form

where 



2.2. Boundary Conditions
Solution of the equations of motion cited before is accomplished by utilizing the convenient boundary conditions. The flow field solutions of the above governing equations have to satisfy the kinematic and dynamic boundary conditions at the two interfaces, which can be taken as

where 
faces are moving with the fluids lead to

In addition the jump in the shearing stresses is zero across the interfaces, this gives

where, 

Furthermore, the Maxwell’s conditions on the magnetic field where no free surface charges are present on the interfaces. The continuity of the normal component of the magnetic displacement at the interfaces reads:

The tangential component of the magnetic field is zero across the interfaces, this requires that from this equation, we have


where, we use the zero order from continuity of the normal component of magnetic field to express both 


The completion of the mathematical description of the problem requires an additional interfacial condition determine the shape of the interface between the fluids, which is the dynamical equilibrium boundary condition in which the surface traction suffers a discontinuity due to the surface tension:

These boundary conditions represented here are prescribed at the interface
2.3. Linear Perturbation and Solutions
The analysis of linear theory, as presented in Chandrasekhar book [18] , depends on neglecting the nonlinear terms from equation of motion as well as from the boundary conditions. The solution of the above system of governing equations and boundary conditions can be facilitated by defining a stream function, y of the time and space coordinates, which automatically satisfies Equation (2), where

To solve the equations for the fluid phases under consideration, the two-dimensional finite disturbances are introduced into the equation of motion and continuity equation as well as the boundary conditions. As a customary in hydrodynamic stability analysis [18] , where all quantities have exponential time and a spatial dependence and in view of a standard Fourier decomposition, we may assume that the solutions are in the form




where 






Eliminating the pressure term from Equations (1) and (2) and using (15) and (17), we obtain the following equation

and
Using the normal mode solution (17) we can obtain the pressure from Equation (1):

Substituting, the solution of the analytical solution of Equation (18) into Equation (15) we get

Also, the solution of the magnetic potential, in view of Equation (5) may be taken the form

Since the disturbances vanish as


3. Results and Discussion
3.1. Derivation of the Characteristic Equation
In this section, we will derive the dispersion relation controlling the stability behavior of the system. When the obtained solutions of the stream function, magnetic potential and surface tension are inserted into Equations (6)- (12), we have a linear homogeneous system of algebraic equations of the fourteen unknown coefficients




where 0 is a null vector, Z is a vector of unknown coefficients defined as

where the superscript T indicates the matrix transpose. A non-trivial solutions of the unknown coefficients



which represents the linear dispersion equation for surface waves propagating through a viscous layer embedded between two other fluids with the influence of constant horizontal magnetic field. This dispersion relation controls the stability in the present problem. That is, each negative of the real part of w corresponds to a stable mode of the interfacial disturbance. On the other hand, if the real part of w is positive, the disturbance will grow in time and the flow becomes unstable.
It is clear that the eigenvalue relation (24) is somewhat more general and quite complex, since 

we get 
braic equation for the frequency w which coincides with that obtained by Kwak and Pozrikidis [19] . Another case is the limiting case of one interface between two continuum layers (non-porous medium), in which highly viscous fluids are considered. Thus we obtain a polynomial equation of fifth order in w, which is obtained before by Kumar and Singh [15] and Sunil et al. [20] .
In the following, numerical applications are carried out to demonstrate the effects of various physical parameters on the stability criteria of the system. In the present work, we will numerically solve the implicit dispersion relation by means of the Chebyshev spectral tau method [21] .
3.2. Numerical Estimation for Stability Configuration
In this section, the goal is to determine the numerical assess for the stability pictures for surface waves propagating through porous media. In order to present this examination, Equation (24) is used to control the stability behavior, which requires specification of the parameters: the magnetic field, the magnetic permeability, the porosity effect, the density, the viscosity. In the calculations given below all the physical parameters are sought in the dimensionless form as defined above. The stability of fluid sheets corresponds to negative values of the disturbance growth rate (i.e.
To show the effect of changes of the magnetic permeability ratio 





Figure 2. Influence of the magnetic permeability 














correspondingly at higher values of the wave number, further the plane 



The examination of the influence of the magnetic field 




The examination of change of the lower to the middle fluid viscosity ratio 






Figure 3. Effects of the magnetic field 


Figure 4. The graph is constructed for 


Figure 5. Represents the stability diagrams in the plane 

Figure 6 exhibits the effects of the the permeability parameter 









The influence of magnetic field 







A conclusion that may be made from the comparison among the parts (a-c) of Figure 7 is that the magnetic field leads to crowd in the concentration of the streamlines in the movement of the fluids. In other words, in the light of stability configuration, we notice that corresponding the parts (a-c) of Figure 7 there are three different values of the disturbance growth rate
Figure 6. Illustrated in the plane 

Figure 7. Streamlines contours for a system having the same parameters considered in Figure 2, with




4. Conclusions
This work is concerned with the influence of the normal magnetic field on the gravitational stability of a viscous fluid sheet of finite thickness. The sheet is embedded between two semi-infinite fluids layers moving in porous media, under the influence of magnetic field. The solutions of the linearized equations of motion under the boundary conditions lead to an implicit dispersion relation between the growth rate and wave number. The parameters governing the layers flow system, the magnetic properties and porosity effects strongly influence the wave forms and their amplitudes and hence the stability of the fluid. The stability criteria have been performed theoretically and numerically in which the physical parameters are put in the dimensionless form. Some stability diagrams have been plotted and discussed, in which the influence of the various parameters of the problem on the interface stability is thoroughly analyzed.
It has been found that the phenomenon of the dual (to be either stabilizing or destabilizing) role is found for increasing the permeability parameter. It is established that both the viscosity coefficient and the magnetic permeability damps the growth rate, introducing stabilizing influence, where a part of its kinetic energy may be absorbed. However, it is expected to be a more careful search would clarify that the motion of the interfacial waves will be more stable with the increase of the values of the viscosity as well as the magnetic permeability. In addition an increase of the lower to the middle fluid viscosity ratio decrease both the growth rate and the stability range of fluid sheet, which give a stabilizing influence on the stability behavior of the waves. This result confirmed the fact that when the lower fluid is more viscous than the upper, thus the system is stable. The role of the magnetic field and Reynolds number is to increase the amplitude of the disturbance leading to the destabilization state of the flow system, promote the oscillatory behavior.
References
- El-Dib, Y.O. (2003) Nonlinear Rayleigh? Taylor Instability for Hydromagnetic Darcian Flow: Effect of Free Surface Currents. Journal of Colloid and Interface Science, 259, 309-321. http://dx.doi.org/10.1016/S0021-9797(02)00208-4
- Bhatia, P.K. (1974) Rayleigh-Taylor Instability of Two Viscous Superposed Conducting Fluids. Nuovo Cimento, 19B, 161-168.
- Funada, T. and Joseph, D.D. (2001) Viscous Potential Flow Analysis of Kelvin-Helmholtz Instability in a Channel. Journal of Fluid Mechanics, 445, 263-283. http://dx.doi.org/10.1017/S0022112001005572
- Elhefnawy, A.F. (1995) Intervals of an Unsteady Electrohydrodynamic Kelvin-Helmoltz Stability. Physica A, 214, 229-241. http://dx.doi.org/10.1016/0378-4371(94)00232-I
- Drazin, P.G. and Reid, W.H. (1981) Hydrodynamic Stability. University Press, Cambridge.
- Joseph, D.D. (1976) Stability of Fluid Motions II. Springer-Verlag, New York.
- Zakaria, K., Sirwah, M.A. and Alkharashi, S. (2008) Temporal Stability of Superposed Magnetic Fluids in Porous Media. Physica Scripta, 77, 1-20. http://dx.doi.org/10.1088/0031-8949/77/02/025401
- Zakaria, K., Sirwah, M.A. and Alkharashi, S.A. (2012) Non-Linear Analysis of Creeping Flow on the Inclined Permeable Substrate Plane Subjected to an Electric Field. International Journal of Non-Linear Mechanics, 47, 577-598. http://dx.doi.org/10.1016/j.ijnonlinmec.2011.11.010
- Wray, A.W., Papageorgiou, D.T. and Matar, O.K. (2013) Electrified Coating Flows on Vertical Fibres: Enhancement or Suppression of Interfacial Dynamics. Journal of Fluid Mechanics, 735, 427-456. http://dx.doi.org/10.1017/jfm.2013.505
- Liu, Z., Brenn, G. and Durst, F. (1998) Linear Analysis of the Instability of Two-Dimensional Non-Newtonian Liquid Sheets. Journal of Non-Newtonian Fluid Mechanics, 78, 133-166. http://dx.doi.org/10.1016/S0377-0257(98)00060-3
- Sirwah, M.A. (2012) Linear Instability of the Electrified Free Interface between Two Cylindrical Shells of Viscoelastic Fluids through Porous Media. Acta Mechanica Sinica, 28, 1572-1589. http://dx.doi.org/10.1007/s10409-012-0208-2
- Tan, W.C. and Masuoka, T. (2005) Stokes’ First Problem for an Oldroyd-B Fluid in a Porous Half Space. Physics of Fluids, 17, Article ID: 023101. http://dx.doi.org/10.1063/1.1850409
- Zakaria, K. (2012) Long Interfacial Waves inside an Inclined Permeable Channel. International Journal of Non-Linear Mechanics, 47, 42-48. http://dx.doi.org/10.1016/j.ijnonlinmec.2012.02.002
- Khan, M., Saleem, M., Fetecau, C. and Hayat, T. (2007) Transient Oscillatory and Constantly Accelerated Non-New- tonian Flow in a Porous Medium. International Journal of Non-Linear Mechanics, 42, 1224-1239. http://dx.doi.org/10.1016/j.ijnonlinmec.2007.09.008
- Kumar, P. and Singh, G.J. (2006) Stability of Two Superposed Rivlin-Ericksen Viscoelastic Fluids in the Presence of Suspended Particles. Romanian Journal of Physics, 51, 927-935.
- Woodson, H.H. and Melcher, J.R. (1968) Electromechanical Dynamics. John Wiley and Sons, Hoboken.
- Rosensweig, R.E. (1985) Ferrohydrodynamics. Cambridge University Press, Cambridge.
- Chandrasekhar, S. (1961) Hydrodynamic and Hydromagnetic Stability. Oxford University Press, Oxford.
- Kwak, S. and Pozrikidis, C. (2001) Effect of Surfactants on the Instability of a Liquid Thread of Annular Layer. Part I: Quiescent Fluids. International Journal of Multiphase Flow, 27, 1-37. http://dx.doi.org/10.1016/S0301-9322(00)00011-2
- Sharma, R.C. and Chandel, R.S. (2002) On Superposed Couple-Stress Fluids in Porous Medium in Hydromagnetics. Zeitschrift für Naturforschung, 57a, 955-960.
- Boyd, J.P. (2001) Chebyshev and Fourier Spectral Methods. Dover Publications Inc., Mineola.
- Ozen, O., Aubry, N., Papageorgiou, D.T. and Petropoulos, P.G. (2006) Electrohydrodynamic Linear Stability of Two Immiscible Fluids in Channel Flow. Electrochimica Acta, 51, 5316-5323. http://dx.doi.org/10.1016/j.electacta.2006.02.002









