Journal of Applied Mathematics and Physics
Vol.02 No.13(2014), Article ID:52436,11 pages
10.4236/jamp.2014.213136

Some Construction Methods of A-Optimum Chemical Balance Weighing Designs

Rashmi Awad*, Shakti Banerjee

School of Statistics, Devi Ahilya University, Indore, India

Email: *awad.rashmi@gmail.com, shaktibn@yahoo.com

Copyright © 2014 by authors and Scientific Research Publishing Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

Received 25 September 2014; revised 26 October 2014; accepted 3 November 2014

ABSTRACT

Some new construction methods of the optimum chemical balance weighing designs and pairwise efficiency and variance balanced designs are proposed, which are based on the incidence matrices of the known symmetric balanced incomplete block designs. Also the conditions under which the constructed chemical balance weighing designs become A-optimal are also been given.

Keywords:

Balance Incomplete Block Design, Symmetric Balanced Incomplete Block Design, Variance Balanced Design, Efficiency Balanced Design, Weighing Design, Chemical Balance Weighing Design, Optimum Chemical Balance Weighing Design, A-Optimal Chemical Balance Weighing Design

1. Introduction

Sir R. A. Fisher, a founder of modern concept of experimental designs gave the new ideas of designing in his first book Design of Experiment in the year 1935. Fisher’s work was continued by others; see [1] - [4] . The necessary and sufficient condition for a general block design to be variance balanced and efficiency balanced was given in the literature [5] - [8] . The concept of repeated blocks was introduced by Van Lint; see [9] . Further some potential applications of the balanced incomplete block designs with repeated blocks were presented in the literature [10] - [13] .

Another important concept which we discuss in this paper is weighing designs. The concept of weighing design was originally given by Yates and formulated as a weighing problem by Hotelling and the condition of attaining the lower bound by each of the variance of the estimated weights was given by him; see [14] [15] . In the latter developments, attention has been made in the direction of obtaining optimum weighing designs. Prominent work has been done by many researchers in this field; see [16] - [20] . In recent years, the new methods of constructing the optimum chemical balance weighing designs and a lower bound for the variance of each of the estimated weights from this chemical balance weighing design were obtained and a necessary and sufficient condition for this lower bound to be attained was proposed in the literature; see [21] - [24] . The constructions were based on the incidence matrices of balanced incomplete block designs, balanced bipartite block designs, ternary balanced block designs and group divisible designs.

Awad et al. [25] [26] gave the construction methods of obtaining optimum chemical balance weighing designs using the incidence matrices of symmetric balanced incomplete block designs and some pairwise balanced designs were also been obtained which were efficiency as well as variance balanced. In that series we now propose another new construction methods of obtaining optimum chemical balance weighing designs using the incidence matrices of symmetric balanced incomplete block designs and some more pairwise efficiency as well as variance balanced designs are proposed. Also we present the conditions under which the chemical balance weighing designs constructed by new construction methods leading to the A-optimal designs.

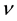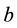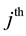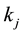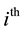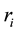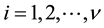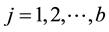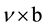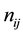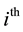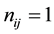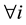Let us consider treatments arranged in blocks, such that the block contains experimental units and the treatment appears times in the entire design,;. For any block design there exist a incidence matrix of order, where denotes the number of experiment units in the block getting the treatment. When or 0 and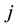, the design is said to be binary. Otherwise it is said to be nonbinary. In this paper we consider binary block designs only. The following additional notations are used is the column vector of block sizes, is the column vector of treatment replication, , , is the total number of experimental units, with this and Where is the vector of ones.

An equi-replicate, equi-block sized, incomplete design, which is also balanced in the sense given above is called balanced incomplete block design, which is an arrangement of symbols (treatments) into sets (blocks) each containing distinct symbols, such that any pair of distinct symbols occurs in exactly sets. Then it is easy to see that each treatment occurs in sets., , , , are called parameters of the BIBD and the parameters satisfies the relations, and (Fisher’s Inequality). A BIB design is said to be symmetric if and. In this case incidence matrix is a square matrix i.e.. In case of symmetric balanced incomplete block design any two blocks have treatments in common.

Though there have been balanced designs in various senses (see [6] [27] ). We will consider a balanced design of the following type.

A block design is called variance balanced if and only if

1) It permits the estimation of all normalized treatment contrasts with the same variance (see [7] ).

2) If the information matrix for treatment effects satisfies.

where is the unique nonzero eigen value of the matrix with the multiplicity, is the identity matrix.

A block design is called efficiency balanced if

1) Every contrast of treatment effects is estimated through the design with the same efficiency factor.

2); see [2] , and since, where is the unique non zero eigen value of with multiplicity. For the EB block design, the information matrix is given as; see [28] .

A block design is said to be pairwise balanced if (a constant) for all, , and a pairwise balanced block design is said to be binary if or 1 only, for all, and it has parameters, , , , (, say) [in this case, when and, it is a BIB design with parameters, , , ,].

Weighing designs consists of groupings of the objects and suppose we want to determine the individual weights of objects. We can fit the results into the general linear model

(1)

where is an random column vector of the observed weights, is the column vector repre- senting the unknown weights of objects and is an random column vector of errors such that and., is a matrix of known quantities. The elements of matrix take the values as

The normal equations estimating are of the form

(2)

where is the vector of the weights estimated by the least squares method.

The matrix is called the design matrix. A weighing design is said to be singular or nonsingular, depending on whether the matrix is singular or nonsingular, respectively. It is obvious that the matrix is nonsingular if and only if the matrix is of full column. Now, if is of full rank, that is, when is nonsingular, the least squares estimate of is given by

(3)

and the variance-covariance matrix of is

(4)

When the objects are placed on two pans in a chemical balance, we shall call the weighings two pan weighing and the design is known as two pan design or chemical balance weighing design. In chemical balance weighing design, the elements of design matrix takes the values as +1 if the object is placed in the left pan in the weighing, if the object is placed in the right pan in the weighing and 0 if the object is not weighted in the weighing.

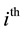
Hotelling has shown that if weighing operations are to determine the weights of objects, the minimum attainable variance for each of the estimated weights in this case is and proved the theorem that each of the variance of the estimated weights attains the minimum if and only if (see [14] ).

2. Variance Limit of Estimated Weights

Let be an matrix of rank of a chemical balance weighing design and let be the number of times in which object is weighed, (i.e. the be the number of elements equal to −1 and 1 in column of matrix). Then Ceranka et al. (see [21] ) proved the following theorem:

Theorem 2.1. For any matrix, of a nonsingular chemical balance weighing design, in which maximum number of elements equal to and 1 in columns is equal to m, where.

Then each of the variances of the estimated weights attains the minimum if and only if

(5)

Also a nonsingular chemical balance weighing design is said to be optimal for the estimating individual weights of objects if the variances of their estimators attain the lower bound given by,

(6)

In SBIB design; the block intersection between any two blocks is constant i.e.. Using this concept Banerjee (see [29] ) proved the following results;

Proposition 2.2. Existence of SBIB design; implies the existence of a BIB design with parameters, , , ,.

Proposition 2.3. Existence of SBIB design; implies the existence of a BIB design with parameters, , , ,.

3. Construction of Design Matrix: Method I

In SBIB design with the parameters, ,; fix the block. Corresponding to the fixed block, give negative sign to all the common treatments of remaining blocks. Then eliminate that fixed block. Thus matrix of design is obtained.

Now doing the same procedure for all the remaining blocks, the incidence matrix of the new design so formed is the matrix having the elements 1, and 0; given as follows

(7)

Then combining the incidence matrix of SBIB design repeated s-times with we get the matrix of a chemical balance weighing design as

(8)

Under the present construction scheme, we have and. Thus the each column of will contain elements equal to 1, elements equal to and elements equal to zero. Clearly such a design implies that each object is weighted times in weighing operations.

Lemma 3.1. A design given by of the form (8) is non singular if and only if.

Proof. For the design matrix given by (8), we have

(9)

and

(10)

the determinant (10) is equal to zero if and only if

or

but is positive and then if and only if . So the lemma is proved. □

Theorem 3.2. The non-singular chemical balance weighing design with matrix given by (8) is optimal if and only if

(11)

Proof. From the conditions (5) and (9) it follows that a chemical balance weighing design is optimal if and only if the condition (11) holds. Hence the theorem.

If the chemical balance weighing design given by matrix of the form (8) is optimal then

Example 3.3. Consider a SBIB design with parameters, ,; whose blocks are gi- ven by (3,5,6,7), (1,4,6,7), (1,2,5,7), (1,2,3,6), (2,3,4,7), (1,3,4,5), (2,4,5,6).

Theorem 3.2 yields a design matrix of optimum chemical balance weighing design as

Clearly such a design implies that each object is weighted times in weighing operations and

for each.

Corollary 3.4. If the SBIB design exists with parameters, ,;

then the design matrix so formed using above method is optimum chemical balance weighing design.

Corollary 3.5. If in the design; is replaced by zero then the new design so formed is a BIB design with parameters, , , ,. Then the structure

(12)

form a pairwise VB and EB design D*1 with parameters

, ,

4. Construction of Design Matrix: Method II

In SBIB design with the parameters, ,; consider the blocks containing any pair of treatments say. Now rearranging the -blocks corresponding to the pair and giving the negative sign to the treatments and both; the matrix of design is obtained.

Now doing the same procedure for all the sets of blocks, the incidence matrix of the new design so formed is the matrix having the elements 1, and 0; given as follows

(13)

Then combining the incidence matrix of SBIB design repeated -times with we get the matrix of a chemical balance weighing design as

(14)

Under the present construction scheme, we have and. Thus the each column of will contain elements equal to 1, elements equal to and elements equal to zero. Clearly such a design implies that each object is weighted times in weighing operations.

Lemma 4.1. A design given by of the form (14) is non singular if and only if.

Proof. For the design matrix given by (14), we have

(15)

and

(16)

the determinant (16) is equal to zero if and only if

or

but is positive and then if and only if . So the lemma is proved. □

Theorem 4.2. The non-singular chemical balance weighing design with matrix given by (8) is optimal if and only if

(17)

Proof. From the conditions (5) and (15) it follows that a chemical balance weighing design is optimal if and only if the condition (17) holds. Hence the theorem.

If the chemical balance weighing design given by matrix of the form (14) is optimal then

Example 4.3. Consider a SBIB design with parameters, ,; whose blocks are given by (1,2,4), (2,3,5), (3,4,6), (4,5,7), (1,5,6), (2,6,7), (1,3,7).

Theorem 4.2 yields a design matrix of optimum chemical balance weighing design as

Clearly such a design implies that each object is weighted times in weighing operations and for each.

Corollary 4.4. If the SBIB design exists with block size and; then the design matrix so formed using above method II is optimum chemical balance weighing design.

Corollary 4.5. If the SBIB design exists with parameters; then the design matrix given by (14) is optimum chemical balance weighing design if and only if.

Corollary 4.6. If in the design; is replaced by zero then the new design so formed is a BIB design with parameters, , , ,. Then the structure

(18)

form a pairwise VB and EB design with parameters

, , , , , ,

5. A-Optimality of Chemical Balance Weighing Design

Some problems related to the optimality of chemical balance weighing designs were considered in the literature;

see [17] [30] [31] . Wong and Masaro [32] [33] gave the lower bound for and some construction methods of the A-optimal chemical balance weighing designs.

Let be a design matrix of a chemical balance weighing design. Then the following results from

Ceranka et al. [34] give the lower bound for.

Theorem 5.1. For any nonsingular chemical balance weighing design with the design matrix we have

(19)

where, ,.

The case when; we get the inequality given in Wong and Masaro [32] .

Definition 5.2. Any nonsingular chemical balance weighing design with the design matrix is said to be A-optimal if

(20)

Theorem 5.3. Any nonsingular chemical balance weighing design with the design matrix is A-optimal if and only if

(21)

6. Checking the A-Optimality in Methods I and II

For the construction Method I of chemical balance weighing design; the Lemma 3.1 proven above gave the necessary condition for the design matrix of the form (8) to be non-singular.

Theorem 6.1. The non-singular chemical balance weighing design with matrix given by (8) is A-optimal if and only if

(22)

(23)

Proof. For the design matrix given in (8) we have

and

Comparing these two equalities we get

and

If (22) is satisfied then we get the condition (23) from the last equation. Hence the theorem.

For the construction Method II of chemical balance weighing design; the Lemma 4.1 proven above gave the necessary condition for the design matrix of the form (14) to be non-singular.

Theorem 6.2. The non-singular chemical balance weighing design with matrix given by (14) is A-op- timal if and only if

(24)

and

(25)

Proof. For the design matrix given in (14) we have

and

Comparing these two equalities we get

and

If (24) is satisfied then we get the condition (25) from the last equation. Hence the theorem.

7. Discussion

The following Table 1 and Table 2 provide the list of pairwise variance and efficiency balanced block designs for Methods I and II respectively, which can be obtained by using certain known SBIB designs.

8. Conclusion

It is well known that pairwise balanced designs are not always efficiency as well as variance balanced. But in this research we have significantly shown that the proposed pairwise balanced designs are efficiency as well as variance balanced. Further there is a scope to propose different methods of construction to obtain the optimum chemical balance weighing designs and pairwise variance and efficiency balanced block designs, which will ful- fill the optimality criteria by means of efficiency. In this research paper we also gave the conditions under which

Table 1. For method I.

Table 2. For method II.

**The symbols and denote the reference number in Raghavrao [30] and Marshal Halls [35] list.

the constructed chemical balance weighing designs lead to A-optimal designs. The only limitation of this research is that the obtained pairwise balanced designs all have large number of replications.

Acknowledgments

We are grateful to the anonymous referees for their constructive comments and valuable suggestions.

References

  1. Agrawal, H.L. and Prasad, J. (1982) Some Methods of Construction of Balanced Incomplete Block Designs with Nested Rows and Columns. Biometrika, 69, 481-483. http://dx.doi.org/10.1093/biomet/69.2.481
  2. Caliski, T. (1971) On Some Desirable Patterns in Block Designs. Biometrika, 27, 275-292. http://dx.doi.org/10.2307/2528995
  3. Hanani, H. (1975) Balanced Incomplete Block Designs and Related Designs. Discrete Mathematics, 11, 255-269. http://dx.doi.org/10.1016/0012-365X(75)90040-0
  4. Shrikhande, S.S. and Raghavarao, D. (1963) A Method of Construction of Incomplete Block Designs. Sankhya, A25, 399-402.
  5. Jones, R.M. (1959) On a Property of Incomplete Blocks. Journal of the Royal Statistical Society, B21, 172-179.
  6. Puri, P.D. and Nigam, A.K. (1975) On Patterns of Efficiency Balanced Designs. Journal of the Royal Statistical Society, B37, 457-458.
  7. Rao, V.R. (1958) A Note on Balanced Designs. Annals of the Institute of Statistical Mathematics, 29, 290-294. http://dx.doi.org/10.1214/aoms/1177706729
  8. Williams, E.R. (1975) Efficiency Balanced Designs. Biometrika, 62, 686-689. http://dx.doi.org/10.2307/2335531
  9. Van Lint, J.H. (1973) Block Designs with Repeated Blocks and (b; r; λ) = 1. Journal of Combinatorics Theory, A15, 88-309.
  10. Ceranka, B. and Graczyk, M. (2007) Variance Balanced Block Designs with Repeated Blocks. Applied Mathematical Sciences, 1, 2727-2734.
  11. Ceranka, B. and Graczyk, M. (2009) Some Notes about Efficiency Balanced Block Designs with Repeated Blocks. Metodoloski Zvezki, 6, 69-76.
  12. Ghosh, D.K. and Shrivastava, S.B. (2001) A Class of Balanced Incomplete Block Designs with Repeated Blocks. Journal of Applied Statistics, 28, 821-833. http://dx.doi.org/10.1080/02664760120074915
  13. Hedayat, A. and Federer, W.T. (1972) Pairwise and Variance Balanced Incomplete Block Designs. Annals of the Institute of Statistical Mathematics, 26, 331-338. http://dx.doi.org/10.1007/BF02479828
  14. Hotelling, H. (1944) Some Improvements in Weighing and Other Experimental Techniques. Annals of Mathematical Statistics, 15, 297-306. http://dx.doi.org/10.1214/aoms/1177731236
  15. Yates, F. (1935) Complex Experiments. Supplement to the Journal of the Royal Statistical Society, 2, 181-247.
  16. Banerjee, K.S. (1948) Weighing Designs and Balanced Incomplete Blocks. Annals of Mathematical Statistics, 19, 394-399. http://dx.doi.org/10.1214/aoms/1177730204
  17. Banerjee, K.S. (1975) Weighing Designs for Chemistry, Medicine, Economics, Operations Research, Statistics. Marcel Dekker Inc., New York.
  18. Dey, A. (1969) A Note on Weighing Designs. Annals of the Institute of Statistical Mathematics, 21, 343-346. http://dx.doi.org/10.1007/BF02532262
  19. Dey, A. (1971) On Some Chemical Balance Weighing Designs. Australian Journal of Statistics, 13, 137-141. http://dx.doi.org/10.1111/j.1467-842X.1971.tb01252.x
  20. Raghavarao, D. (1959) Some Optimum Weighing Designs. Annals of Mathematical Statistics, 30, 295-303. http://dx.doi.org/10.1214/aoms/1177706253
  21. Ceranka, B. and Graczyk, M. (2001) Optimum Chemical Balance Weighing Designs under the Restriction on the Number in Which Each Object Is Weighed. Discussiones Mathematicae: Probability and Statistics, 21, 113-120.
  22. Ceranka, B. and Graczyk, M. (2002) Optimum Chemical Balance Weighing Designs Based on Balanced Incomplete Block Designs and Balanced Bipartite Block Designs. Mathematica, 11, 19-27.
  23. Ceranka, B. and Graczyk, M. (2004) Ternary Balanced Block Designs Leading to Chemical Balance Weighing Designs for v + 1 Objects. Biometrica, 34, 49-62.
  24. Ceranka, B. and Graczyk, M. (2010) Some Construction of Optimum Chemical Balance Weighing Designs. Acta Universitatis Lodziensis, Folia Economic, 235, 235-239.
  25. Awad, R. and Banerjee, S. (2013) Some Construction Methods of Optimum Chemical Balance Weighing Designs I. Journal of Emerging Trends in Engineering and Applied Sciences (JETEAS), 4, 778-783.
  26. Awad, R. and Banerjee, S. (2014) Some Construction Methods of Optimum Chemical Balance Weighing Designs II. Journal of Emerging Trends in Engineering and Applied Sciences (JETEAS), 5, 39-44.
  27. Caliski, T. (1977) On the Notation of Balance Block Designs. In: Recent Developments in Statistics, North-Holland Publishing Company, Amsterdam, 365-374.
  28. Kageyama, S. (1974) On Properties of Efficiency Balanced Designs. Communications in Statistics-Theory and Methods, 9, 597-616.
  29. Banerjee, S. (1985) Some Combinatorial Problems in Incomplete Block Designs. Unpublished Ph.D. Thesis, Devi Ahilya University, Indore.
  30. Raghavarao, D. (1971) Constructions and Combinatorial Problems in Designs of Experiments. John Wiley, New York.
  31. Shah, K.R. and Sinha, B.K. (1989) Theory of Optimal Designs. Springer-Verlag, Berlin, Heidelberg. http://dx.doi.org/10.1007/978-1-4612-3662-7
  32. Wong, C.S. and Masaro, J.C. (1984) A-Optimal Design Matrices with, 0, 1. Linear and Multilinear Algebra, 15, 23-46. http://dx.doi.org/10.1080/03081088408817576
  33. Jacroux, M., Wong, C.S. and Masaro, J.C. (1983) On the Optimality of Chemical Balance Weighing Designs. Journal of Statistical Planning and Inference, 8, 231-240. http://dx.doi.org/10.1016/0378-3758(83)90041-1
  34. Ceranka, B. and Graczyk, M. (2007) A-Optimal Chemical Balance Weighing Design under Certain Conditions. Metodoloski Zvezki, 4, 1-7.
  35. Hall Jr., M. (1986) Combinatorial Theory. John Wiley, New York.

NOTES

*Corresponding author.

Journal Menu >>