Received 13 June 2014; revised 15 July 2014; accepted 26 July 2014

ABSTRACT

We establish the existence of positive solutions for singular boundary value problems of coupled systems

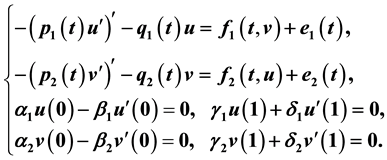
The proof relies on Schauder’s fixed point theorem. Some recent results in the literature are generalized and improved.

Keywords:

Positive Solutions, Second-Order Boundary Value Problems, Coupled Systems, Schauder’s Fixed Point Theorem

1. Introduction

In this paper, we consider the existence of positive solutions for coupled singular system of second order ordinary differential equations

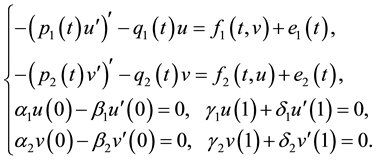(1.1)

Throughout this paper, we always suppose that

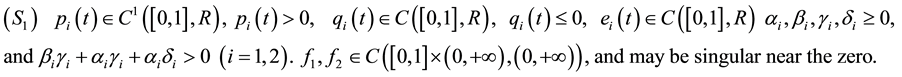
In recent years, singular boundary value problems to second ordinary differential equations have been studied extensively (see [1] -[3] ). Some classical tools have been used in the literature to study the positive solutions for second order singular boundary value problems of a coupled system of differential equations. These classical methods include some fixed point theorems in cones for completely continuous operators and Schauder fixed point theorem, for example, see [4] -[6] and literatures therein. Motivated by the recent work on coupled systems of second-order differential equations, we consider the existence of singular boundary value problem. By means of the Schauder fixed point theorem, we study the existence of positive solutions of coupled system (1.1).

2. Preliminary

We consider the scalar equation

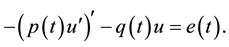(2.1)

with boundary conditions

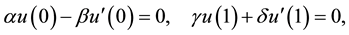(2.2)

Suppose that 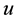is a positive solution of (2.1) and (2.2). Then

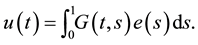
where can be written by

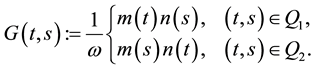
here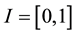, 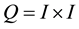and,.

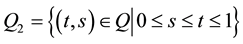Lemma 2.1. Suppose that holds, then the Green’s function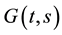, defined by (2.3) possesses the following properties:

1): 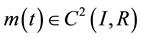is increasing and.

2): is decreasing and.

3):.

4):.

5): is a positive constant. Moreover,.

6): is continuous and symmetrical over.

7): has continuously partial derivative over,.

8): For each fixed, satisfies for,. Moreover, for.

9): has discontinuous point of the first kind at and

We define the function by

which is the unique solution of

Following from Lemma and, it is easy to see that

Let us fix some notation to be used in the following: For a given function, we denote the essential supremum and infimum by and. if they exist. Let, ,.

3. Main Results

1),.

Theorem 3.1. We assume that there exists, , and such that

If, , then there exists a positive solution of (1.1).

Proof A positive solution of (1.1) is just a fixed point of the completely continuous map defined as

By a direct application of Schauder’s fixed point theorem, the proof is finished if we prove that A maps the closed convex set defined as

into itself, where, are positive constants to be fixed properly. For convenience, we introduce the following notations

Given, by the nonnegative sign of and, we have

Note for every

Similarly, by the same strategy, we have

Thus if are chosen so that

Note that, and taking, , , it is sufficient to find such that

and these inequalities hold for big enough because.

2),.

The aim of this section is to show that the presence of a weak singular nonlinearity makes it possible to find positive solutions if,.

Theorem 3.2. We assume that there exists, , and such that is satisfied. If, and

(3.1)

then there exists a positive solution of (1.1).

Proof In this case, to prove that it is sufficient to find, such that

(3.2)

(3.3)

If we fix, , then the first inequality of (3.3) holds if satisfies

or equivalently

The function possesses a minimum at

Taking, then (3.3) holds if

Similarly,

possesses a minimum at

Taking, , then the first inequalities in (3.2) and (3.3) hold if and, which are just condition (3.1). The second inequalities hold directly from the choice of and, so it

remains to prove that, This is easily verified through elementary computations:

since, Similarly, we have.

3)

Theorem 3.3. Assume that is satisfied. If, and

(3.4)

where is a unique positive solution of equation

(3.5)

then there exists a positive solution of (1.1).

Proof We follow the same strategy and notation as in the proof of ahead theorem. In this case, to prove that, it is sufficient to find, such that

(3.6)

(3.7)

If we fix, then the first inequality of (3.6) holds if satisfies

(3.8)

or equivalently

(3.9)

If we chose small enough, then (3.9) holds, and is big enough.

If we fix then the first inequality of (3.7) holds if satisfies

or equivalently

(3.10)

According to

we have, , then there exists such that, and

Then the function possesses a minimum at, i.e.,.

Note then we have

or equivalently

Taking, then the first inequality in (3.7) holds if, which is just condition (3.4). The second inequalities hold directly by the choice of, and it would remain to prove that and. These inequalities hold for big enough and small enough.

Remark 1. In theorem 3.3 the right-hand side of condition (3.4) always negative, this is equivalent to proof that. This is obviously established through the proof of Theorem 3.3.

Similarly, we have the following theorem.

Theorem 3.4. Assume is satisfied. If, and

where is a unique positive solution of the equation

then there exists a positive solution of (1.1).

Funding

Project supported by Heilongjiang province education department natural science research item, China (12541076).

References