Journal of Applied Mathematics and Physics
Vol.2 No.7(2014), Article
ID:46805,7
pages
DOI:10.4236/jamp.2014.27058
Some Results on Riemannean Multiple Barycenters
Mostafa Zahri*, Naji Khallaf
Department of Mathematics, College of Science, Taibah University, Madinah, Saudi Arabia
Email: *zahri@gmx.net, drnaji123@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 March 2014; revised 11 April 2014; accepted 18 April 2014
ABSTRACT
A characteristic of a special case of Riemannean barycenters on the unit circle is presented. The non-uniqueness of such barycenters leads to an interesting study of the so-called multiple barycenters. In this work, we deal with a smooth one-dimensional manifold S1 only. Some theoretical and computational analysis is listed.
Keywords:Smooth Manifold, Geodesic, Barycenter of Masses, Metric Space, Multiple Barycenters

1. Introduction
The Riemanean geometry is the study of curved surfaces. One might have a cylinder, or a sphere. For instance, one can use a cardboard paper towel roll to study a cylinder and a globe to study a sphere. In such spaces, the shortest curve between any pair of mass points on such curved surface is called a minimal geodesic or geodesic. One can find a geodesic between two mass points by stretching a rubber band between them. The first thing that will be noticed is that sometimes there is more than one minimal geodesic between two mass points. For instance, there are many minimal geodesics between the north and south poles of a sphere. This leads to derive more generalized formulas, which are true in the Euclidean space. Therefore, one of our main concern in this work is to motivate researcher for finding exact formulas for computing Barycenters on non-Euclidean spaces, namely on manifolds. In [1] , the authors suggest an estimation of the so-called Riemannean Barycenters. For a use in the same context, we refer for instance to [2] . Where, in [3] Riemannian means were presented as solution of variational problems. We think that for special case, for instance smooth manifolds, we could derive similar formulas to the Euclidean case, define and study interesting properties of Riemannean Barycenters.
In this work, we begin by setting out some basic theory of the geodesic of the unit circle as one dimensional manifold, we define the multiple Barycenters and compute it for some special cases. For more details, we refer to [4] -[6] .
Let I be an interval of real numbers. Then, a curve γ is a continuous mapping given as  where
where ![]() is a smooth Riemannean manifold. The curve γ is said to be simple if it is injective. If I is a closed bounded interval [a, b], we also allow the possibility
is a smooth Riemannean manifold. The curve γ is said to be simple if it is injective. If I is a closed bounded interval [a, b], we also allow the possibility  (this convention makes it possible to talk about closed simple curve). If
(this convention makes it possible to talk about closed simple curve). If  for some
for some  (other than the extremities of I), then
(other than the extremities of I), then  is called a double (or multiple) point of the curve. A curve γ is said to be closed or a loop if I = [a, b] and if
is called a double (or multiple) point of the curve. A curve γ is said to be closed or a loop if I = [a, b] and if . A closed curve is thus a continuous mapping of the circle. Let x, y are two points of
. A closed curve is thus a continuous mapping of the circle. Let x, y are two points of ![]() subset of
subset of . If γ is a curve such that
. If γ is a curve such that ,
,  and
and ![]()
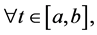 we said that γ is a connection between x and y. We define
we said that γ is a connection between x and y. We define ![]() the set of all connections between x and y on
the set of all connections between x and y on![]() . Let x, y be two mass points of
. Let x, y be two mass points of![]() . The geodesic is the minimum distance between x and y on
. The geodesic is the minimum distance between x and y on ![]() (or the shortest path), denoted by
(or the shortest path), denoted by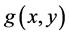 , which is given by
, which is given by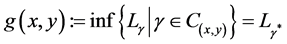 . We say that X is a geodesic space if for any pair
. We say that X is a geodesic space if for any pair  there is a minimal geodesic from x to y and this is given as a minimal of
there is a minimal geodesic from x to y and this is given as a minimal of , where
, where 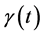 is a curve joining x and y. Let two points
is a curve joining x and y. Let two points . The geodesic (shortest path) between the two points x and y is given by
. The geodesic (shortest path) between the two points x and y is given by , where
, where , is the scalar product on
, is the scalar product on . The shortest geodesic (which is a metric on
. The shortest geodesic (which is a metric on ![]() that joins two non antipodal points. The geodesic distance between the two points is precisely equal to α. A midpoint m of two masses on
that joins two non antipodal points. The geodesic distance between the two points is precisely equal to α. A midpoint m of two masses on ![]() is defined
is defined 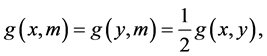 where g is a geodesic on
where g is a geodesic on![]() . For more details, we refer to [7] -[9] .
. For more details, we refer to [7] -[9] .
Example 1. Consider the following examples on the unit circle:
1) Each point on ![]() is midpoint of itself
is midpoint of itself 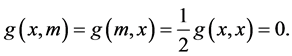
2) The midpoint of  and
and  is the unique point
is the unique point , therefore
, therefore
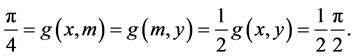
3) Observe that even if  for
for . The fact that
. The fact that  is not a geodesic between x and y.
is not a geodesic between x and y.
4) The midpoint on ![]() is not unique: Consider
is not unique: Consider 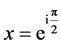 (north pole) and
(north pole) and  (south pole),
(south pole),
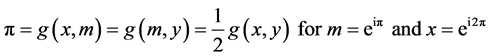 .
.
2. Barycenters on 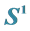
The arithmetic mean of a finite set of mass points  the Euclidean space
the Euclidean space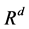 . is the unique point x that minimizes the sum of the squared distances to the given mass point, that is
. is the unique point x that minimizes the sum of the squared distances to the given mass point, that is , where d(·,·)
, where d(·,·)
is an Euclidean distance in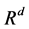 . The point realizing the minimum of the function
. The point realizing the minimum of the function 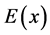 is called also Barycenter of the set of mass points
is called also Barycenter of the set of mass points![]() . In this section we would like to extend this definition to a smooth Riemannean manifold
. In this section we would like to extend this definition to a smooth Riemannean manifold![]() , and for more information, we refer to [1] [3] .
, and for more information, we refer to [1] [3] .
Definition 1. The Barycenter of the set of mass points  subset
subset ![]() with weighs
with weighs 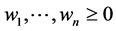 (respectively) is the mass point minimizing the following functional (Energy function):
(respectively) is the mass point minimizing the following functional (Energy function):

where g(·,·) is the geodesic in ![]() and μ is the distribution in the continuous case.
and μ is the distribution in the continuous case.
Lemma 1. Let ![]() and
and  are two mass points with weights
are two mass points with weights ![]() and
and , such that
, such that 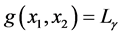
with![]() ,
, 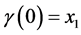 and
and . If
. If ![]() is the geodesic Barycenter of
is the geodesic Barycenter of  in
in![]() , then there exists
, then there exists  such that
such that 
Proof. We prove that the geodesic Barycenter of two mass points is a mass point contained on the shortest path. We have

Suppose that ![]() is not element of
is not element of . There exists
. There exists 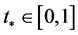 such that
such that

it follows
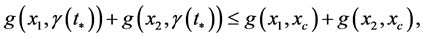
(![]() is not element of
is not element of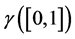 ). It implies
). It implies

In fact, the point ![]() satisfies the minimal and the following equality
satisfies the minimal and the following equality 
Lemma 2. Let two mass points 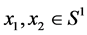 with weights
with weights ![]() and
and  respectively. If for all
respectively. If for all 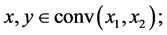
 are unique, then the geodesic Barycenter of
are unique, then the geodesic Barycenter of 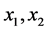 is unique.
is unique.
Proof. Suppose that the Barycenter is not unique, and denote by ![]() and
and ![]() solving the energy functional. From Lemma 1, we know that the geodesic Barycenter is contained on the shortest path between
solving the energy functional. From Lemma 1, we know that the geodesic Barycenter is contained on the shortest path between , it means
, it means
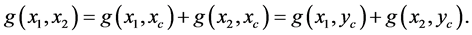
 there exists two geodesics connecting
there exists two geodesics connecting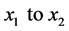 , this contradicts the uniqueness of the geodesic.
, this contradicts the uniqueness of the geodesic.
Definition 2. Let an oriented unit circle with origin![]() , and a subset of mass points points
, and a subset of mass points points
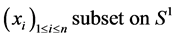 . We denote by
. We denote by  the number of all geodesics, their corresponding curves contain the origin
the number of all geodesics, their corresponding curves contain the origin  where
where 
3. Geodesic Multiple Barycenters on 
The existence of Barycenters on ![]() interpreted as one dimensional Riemannean space does assure it uniqueness. In this section, we give a general condition of the existence of a geodesic multiple Barycenter on
interpreted as one dimensional Riemannean space does assure it uniqueness. In this section, we give a general condition of the existence of a geodesic multiple Barycenter on![]() .
.
Definition 3. (Geodesic Multiple Barycenter). We said that a set of mass points have a multiple Barycenter if the solution of the energy function is not unique.
Example 2.
1) The Barycenter of the north and south poles is not unique i.e. 0 and .
.
2) We examine a simple example on the unit circle. Compute the Barycenter of four mass points


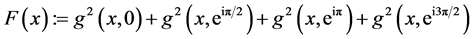
Define 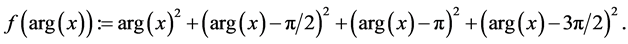
It implies
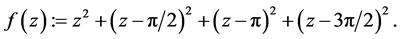
Differentiations with respect to z
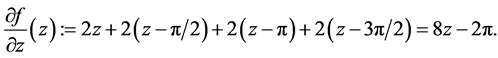
1)  with
with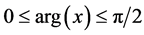 :
:
From 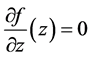 it follows
it follows 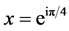 and
and .
.
2)  with
with :
:
From 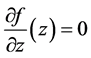 it follows
it follows  and
and .
.
3) 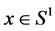 with
with :
:
From  it follows
it follows  and
and .
.
4) 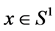 with
with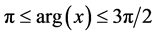 :
:
From 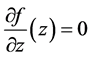 it follows
it follows  and
and .
.
We conclude that 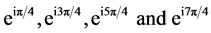 4 are Barycenters of the set X.
4 are Barycenters of the set X.
Definition 4. (Symmetry propriety SP). Let ![]() be a mass distribution on the unit circle. The map
be a mass distribution on the unit circle. The map  is called a symmetry of
is called a symmetry of ![]() if: σ is an isometry and
if: σ is an isometry and 
Example 3.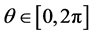 , for which
, for which ![]() satisfies the map
satisfies the map

the symmetry propriety.
The mass distribution is defined on two points
 ,
,  on
on  such that
such that 

It is clear that for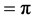 ,
,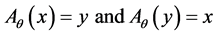 . If the distribution is defined over the set of equidistant masses
. If the distribution is defined over the set of equidistant masses  then for
then for 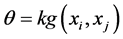 with
with  -rotation on the unit circle, with a supplementary propriety that
-rotation on the unit circle, with a supplementary propriety that 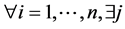 such that
such that 
Figure 1 shows some example of symmetry mass points on  (From left to right) On the first figure, we have two mass points antipodal, the first on (1, 0) Cartesian coordinate and the second in (0, 1). The second, third and fourth show other types of semmetries.
(From left to right) On the first figure, we have two mass points antipodal, the first on (1, 0) Cartesian coordinate and the second in (0, 1). The second, third and fourth show other types of semmetries.
Theorem 1 (Multiple Barycenter). Let 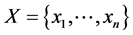 on
on ![]() be a set of n mass points. If there exists a symmetry map Aθ, then x admits a multiple Barycenter.
be a set of n mass points. If there exists a symmetry map Aθ, then x admits a multiple Barycenter.
Proof. For n = 2 and 
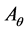 is the symmetry map such that
is the symmetry map such that . Then for all
. Then for all
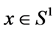 hold,
hold,
![]()
It follows from our assumptions that  for all
for all 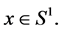 It is clear that
It is clear that 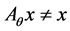 for all
for all
 and if for all
and if for all ![]() is a Barycenter of for all
is a Barycenter of for all 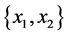 then
then  is too. In this case we have double Barycenters. Now suppose that n > 2. Then, for all
is too. In this case we have double Barycenters. Now suppose that n > 2. Then, for all 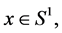 we have
we have

Moreover
Thus
![]()
Lemma 3. Under the same assumptions of Theorem 1. Let k be the number of the symmetry maps  in S1 which have the propriety
in S1 which have the propriety , i.e. the distribution of the mass points is
, i.e. the distribution of the mass points is  -invariant. The number of the multiple Barycenters is k + 1.
-invariant. The number of the multiple Barycenters is k + 1.
Proof. The proof is left to the reader.
Figure 2 contains three, four, five, six, eight and nine mass points satisfying the symmetry property and non necessary with same weights. The geodesic between two arbitrary and successive mass points is constant. I each of the figures our code generates all possible Barycentes so-called multiple Barycenters.
Figure 3 shows the uniqueness of the Barycenter on ![]() in the case of four masses without symmetry property.
in the case of four masses without symmetry property.

Figure 1. Examples of symmetry masses distribution on S1.

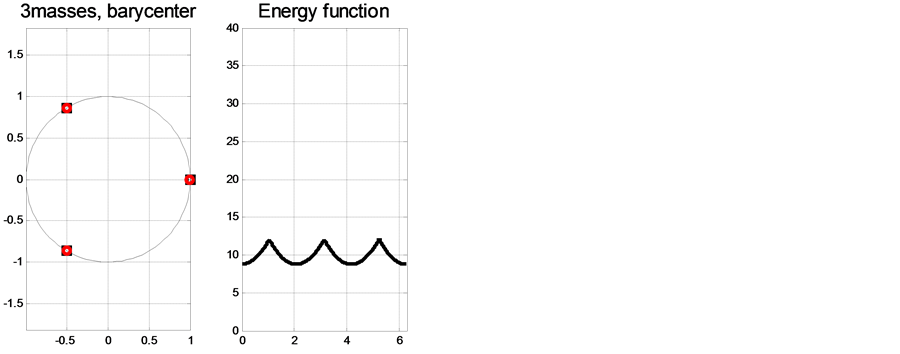


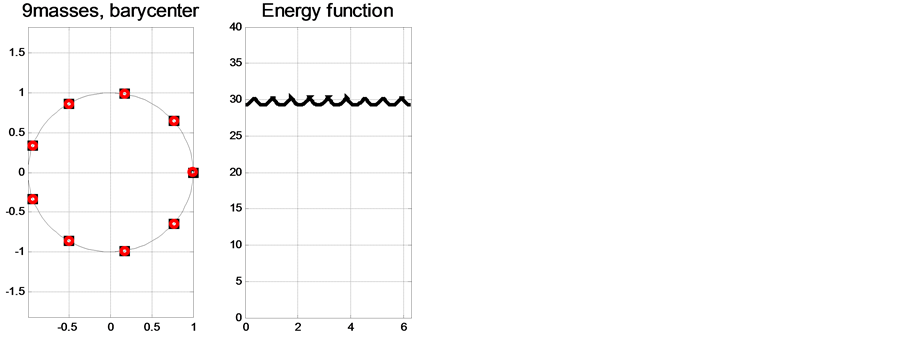
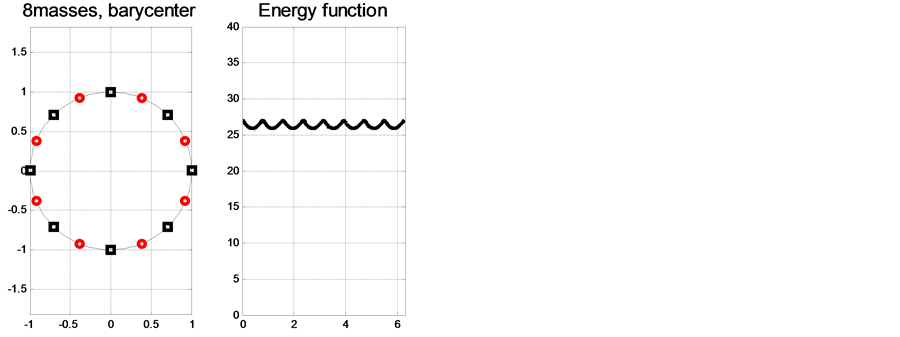
Figure 2. Examples of geodesic multiple Barycenters on S1.
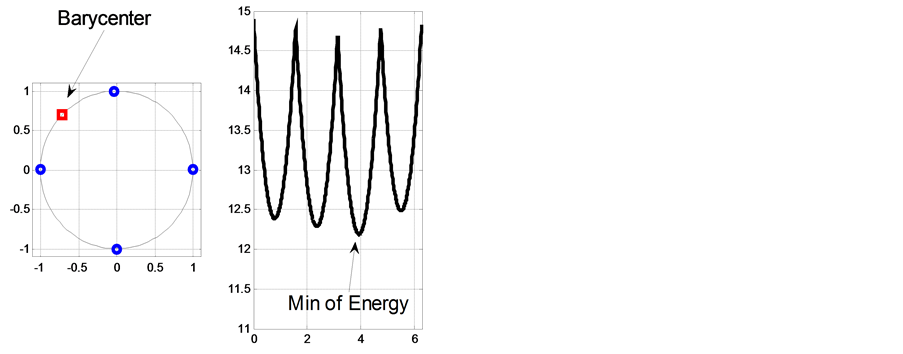
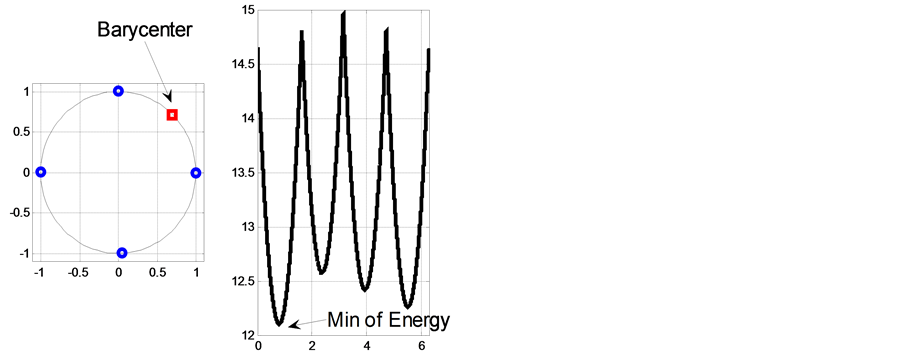
Figure 3. Case of non-symmetry on S1 (uniqueness of the Barycenter. (small perturbation of the north and south poles respectively.
4. Concluding Remarks
As consequence of the non-uniqueness geodesic between two arbitrary mass points, we have presented an example on the notion of multiple Barycenters. Moreover, we have derived some properties similarly to the Euclidean space. We believe that more interesting cases are to construct significant formulas for arbitrary manifolds.
Acknowledgements
The authors would like to dedicate this work to Dr. Musaed Al-Subhi Rahimaho Allah.
References
- Le, H.L. (2004) Estimation of Riemannean Barycenters. LMSJ. Mathematics of Computation, 7.
- Ruedi, F. and Ruh, E.A. (2006) Barycenter and Maximum Likelihood. Differential Geometry and Its Applications, 24, 660-669. http://dx.doi.org/10.1016/j.difgeo.2006.08.009
- Machado, L., Leite, F.S. and Hupner, K. (2006) Riemannean Means as Solution of Variational Problems. LMSJ. Mathematics of Computation, 7.
- Ballman, W., Gromov, M. and Schroeder, V. (1985) Manifolds of Nonpositive Curvature. Birkhauser, Boston. http://dx.doi.org/10.1007/978-1-4684-9159-3
- Kendall, W.S. (1992) The Propeller: A Counter Example to a Conjectured Criterion for the Existence of Certain Harmonic Functions. Journal of the London Mathematical Society, 46, 364-374.
- Evans, L. and Gariepy, R. (1992) Measure Theory and Fine Properties of Functions. Advanced Mathematical Studies, CRC Press, Boca Raton.
- Chen, B.-Y. and Jiang, S. (1995) Inequalities between Volume, Center of Mass, Circumscribed Radius, Order, and Mean Curvature. Bulletin of the Belgian Mathematical Society, 2, 75-86.
- Benedetti, R. and Petronio, C. (1992) Lectures on Hyperbolic Geometry. Universitext, Springer-Verlag, Berlin. http://dx.doi.org/10.1007/978-3-642-58158-8
- Heintze, E. and Im Hof, H.C. (1977) Geometry of Horospheres. Journal of Differential Geometry, 12, 481-491
NOTES

*Corresponding author.

