International Journal of Intelligence Science
Vol.05 No.02(2015), Article ID:53707,12 pages
10.4236/ijis.2015.52009
Modeling Neuromorphic Persistent Firing Networks
Ning Ning1*, Guoqi Li2,3*, Wei He1, Kejie Huang4, Li Pan1, Kiruthika Ramanathan1, Rong Zhao4, Luping Shi2,3
1Data Storage Institute, Agency for Science, Technology and Research, Singapore
2Department of Precision Instrument, Tsinghua University, Beijing, China
3Center for Brain-Inspired Computing Research (CBICR), Tsinghua University, Beijing, China
4Singapore University of Technology and Design, Dover, Singapore
Email: lpshi@tsinghua.edu.cn
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 January 2015; accepted 23 January 2015; published 30 January 2015
ABSTRACT
Neurons are believed to be the brain computational engines of the brain. A recent discovery in neurophysiology reveals that interneurons can slowly integrate spiking, share the output across a coupled network of axons and respond with persistent firing even in the absence of input to the soma or dendrites, which has not been understood and could be very important for exploring the mechanism of human cognition. The conventional models are incapable of simulating the important newly-discovered phenomenon of persistent firing induced by axonal slow integration. In this paper, we propose a computationally efficient model of neurons through modeling the axon as a slow leaky integrator, which captures almost all-known neural behaviors. The model controls the switching of axonal firing dynamics between passive conduction mode and persistent firing mode. The interplay between the axonal integrated potential and its multiple thresholds in axon precisely determines the persistent firing dynamics of neurons. We also present a persistent firing polychronous spiking network which exhibits asynchronous dynamics indicating that this computationally efficient model is not only bio-plausible, but also suitable for large scale spiking network simulations. The implications of this network and the analog circuit design for exploring the relationship between working memory and persistent firing enable developing a spiking network- based memory and bio-inspired computer systems.
Keywords:
Neuron Model, Neuromorphic, Persistent Firing, Slow Integration, Spiking Network, Working Memory

1. Introduction
Understanding how human brain represents, stores, and processes information is one of the greatest unsolved mysteries and fundamental challenges of science today. Over the past century, since Lapicque introduced the integrate-and-fire model of the neuron in 1907 [1] , computational neuroscientists have developed several mathe- matical and computational neural models. Generally, one approach in computational neuroscience involves creating biologically realistic models, where information about the biological details of neurons including their electrochemistry, biochemistry, and detailed morphology and connectivity are also included [2] , such as Hodg- kin-Huxley [3] and compartment models [4] . Another approach involves building qualitative models to capture the spiking nature and the essential elements of the behavior with simplified complexity, for example, leaky in- tegrate-and-fire [5] , FitzHugh-Nagumo [6] , Morris-Lecar [7] , Hindmarsh-Rose [8] , Wilson [9] , Resonate-and- Fire [10] and Izhikevich [11] neuron models.
However, as neuroscience continues to advance rapidly, more and more complex neuronal behaviors and brain dynamics are revealed. This has posed challenges for neural modeling as conventional neuron models fail to reflect the newly-discovered complexity of neural systems, such as the persistent firing phenomenon recently observed in rodent hippocampal inhibitory neurons [12] . In the classic viewpoint about the information flow in the nervous system, synaptic inputs are received and integrated in the dendrites only on a timescale of millise- conds to seconds, and when the depolarized somatic membrane potential exceeds the threshold, action potentials are triggered at the axon hillock and propagate along the axon. However, recent discovery reveals that some ac- tion potential began at the distal end of axon instead of at the axon hillock. A much slower form of potential in- tegration is observed which leads to persistent firing in distal axons of rodent hippocampal and neocortical in- terneurons [12] . The slow integration lasts from tens of seconds to minutes in distal axon, so does the persistent firing. During the persistent firing, the somatic depolarization is not observed, implying that axon may perform its own neural computations without any involvement of the soma or dendrites.
In this paper, we propose a new computationally-efficient artificial neuron model that account for all-known neural behaviors. In this model, axon is an independent computational unit complementary to the classic somatic computational unit which evokes action potentials. Compared to the soma which integrates dendritic inputs in a timescale of milliseconds to seconds, the axon integrates the spikes evoked by soma in a timescale of tens of second to minutes, and consequently determines the persistent firing behavior of the axon. Besides the computa- tional model, a neuromorphic model of persistent firing neurons and its analog circuit are also proposed. In ad- dition, a polychronous spiking network [13] with persistent firing inhibitory interneurons is simulated, which may assist the development of spiking network-based memory and bio-inspired computer system.
2. Persistent Firing Neuron Model
The conventional models such as Izhikevich neuron model [11] are incapable of simulating the important newly- discovered phenomenon of persistent firing induced by axonal slow integration, as a recent discovery in neuro- physiology reveals that interneurons can slowly integrate spiking, share the output across a coupled network of axons and respond with persistent firing even in the absence of input to the soma or dendrites. To this end, we extend the Izhikevich neuron model by modeling the axonal slow integration, which can be mathematically de- scribed by Equations (1)-(6):
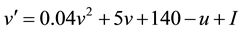 (1)
(1)
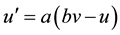 (2)
(2)
 (3)
(3)
with the auxiliary resettings:
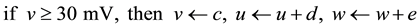 (4)
(4)
 (5)
(5)
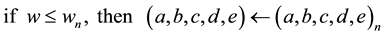 (6)
(6)
where ,
, 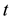 is the time,
is the time,  describes the hyper theoretical potential of the axonal leaky integrator,
describes the hyper theoretical potential of the axonal leaky integrator, 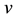 and
and 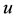 are the dimensionless variables that describe the membrane potential, the membrane recovery, respec- tively. Parameters
are the dimensionless variables that describe the membrane potential, the membrane recovery, respec- tively. Parameters 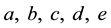 and
and  are dimensionless,
are dimensionless, 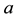 describes the timescale of
describes the timescale of ,
, 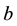 represents the sensitivity of
represents the sensitivity of 
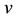
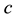


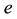
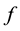
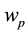
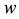


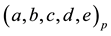


This model extends the Izhikevich neuron model [11] described by Equations (1)-(2), which well captures the somatic spiking dynamics. By modifying the 
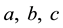
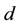
The axon is modeled as a slow leaky integrator, which is capable to alter the axonal functions between passive conduction and persistent firing modes, depending on the potential of axonal integrator. In the passive conduc- tion mode, the axon acts as a transmission cable in which stable propagation occurs once an action potential is evoked by synaptic inputs. In the persistent firing mode, in which the parameters in the model are chosen to set the dynamical system to be self-oscillatory, axon acts as a bistable oscillator which does not require stimulus from dendrites to sustain the persistent firing of action potentials.
In contrast to the somatic leaky integrator which accounts for the integration of dendritic inputs, the axonal leaky integrator has a larger time constant for its integration and leakage, integrating incoming spikes generated in the axon hillock in the timescale from tens of seconds to minutes, due to its slow rate of leakage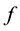
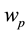




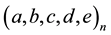
We have simulated the persistent firing neuronal behaviors under two stimulation protocols, with the parame- ters summarized in Table 1. The simulation results under step/pause stimulation protocol [12] are shown in Figure 1. We applied 1-second current step of 500 pA during each 10-second sweep to the simulation model. During the sweeps of the step/pause input stimulus, it is observed that the somatically evoked action potentials appear when the synaptic input stimulus is presented and disappear when the stimulus is removed (Figure 1(a)). When 





The variation of persistent firing frequency was also simulated (Figure 1(b) and Figure 1(c)). As the firing frequency can be tuned by the parameter 
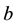

Table 1. Simulation parameters.
Figure 1. Simulation of persistent firing neuron model. (a) The waveform of membrane potential. The simulation used the same stimulation protocol as the experiment of whole-cell current-clamp recording by Sheffield et al [12] . To evoke persistent firing, 1-s current step of 500 pA was delivered to the neuron during each 10-s sweep (left, sweeps 1 - 6; right, sweeps 7 - 12). In this simulation, persistent firing was evoked after the 12th sweep, and the total number of evoked action potentials before persistent firing was 1278. (b) The waveform of persistent firing, which lasted over 2 minutes. The total number of evoked axonal action potentials was 3073. The simulation reflects the decrease of instantaneous firing frequency, which was shown in the current-clamp experiment. (c) The instantaneous firing frequency of persistent firing action potentials, which decreased from 40 Hz at the onset of persistent firing to 12 Hz at the end of persistent firing as the parameter 


The instantaneous firing frequency of axon-evoked action potentials attains its maximum (40 Hz) at the onset of persistent firing, and decreases over time till the end of persistent firing.
We also applied the stimulation with a 40-second long pulse of 15 pA current to the persistent firing neuron model described by Equations (1)-(7) with a different parameter set (Table 1). The simulation results are shown in Figure 2. The repeated somatic current stimuli eventually trigger the persistent firing that outlasts the current stimuli by more than 30 seconds.
By tuning the parameters of 

3. Model Analysis
In this section, we present the mathematical analysis on the conditions which guarantee the existence of the persistent firing behavior in the neuron. Let
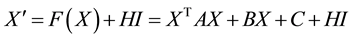
where 
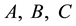

Figure 2. Simulation of persistent firing neuronal behaviors with long pulse stimulation protocol. (a) The input stimulus. A pulse of current with 15 pA amplitude lasts 40 seconds as the synaptic input to the neuron. (b) Time response of
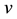

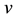
Equations (1)-(3). When the input current 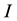


Here, we assume that 

is unstable. Based on the analysis of stability of the equilibrium points and the nonlinear dynamic characteristic of Equation (8), the following conditions can be summarized to guarantee the existence of the persistent firing behavior.
Condition 1. The input current 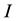
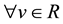


Condition 2. The condition 

Condition 3. When

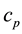
period) is chosen to be the value such that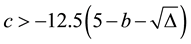
Condition 1 means that there is no equilibrium point for the equation 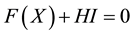
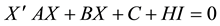




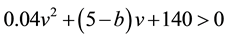

In the above analysis, we choose 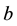

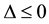

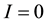

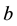

The geometrical approach provides a clear and insightful perspective of investigating the characteristics of dynamical system of neuron [15] , and is therefore adopted to analyze the persistent firing model. We choose conveniently to conduct geometrical analysis on the phenomenon of persistent firing due to a long-lasting pulse stimulation (Figure 2 and Figure 3(a)) rather than on that due to a pulse train (Figure 1), since the geometry of the former is less complicated yet retains significant information regarding the time evolution of the dynamical
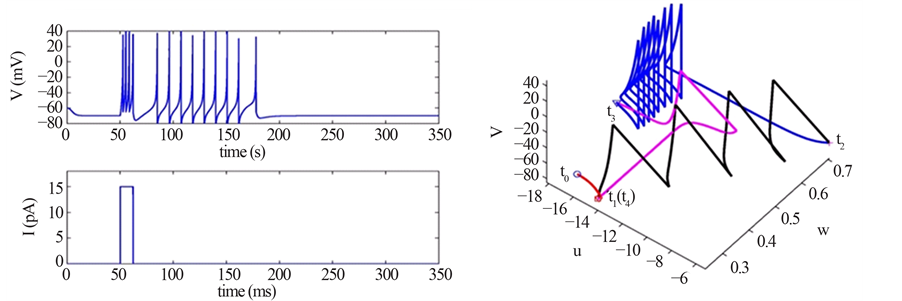

Figure 3. (a) Persistent firing induced by an input current pulse; (b) Trajectory of state variables 
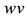
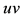
system of neuron, such as the stable equilibrium and the threshold values, as shown in Figure 3(b) where the geometrical trajectory of the state variables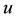

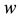
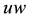


Stage 1: During the time range of
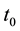
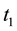

Stage 2: During the time range of
Stage 3: During the time range of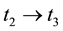

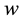
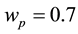
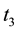
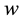

Stage 4: During the time range of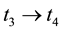
4. Neuromorphic Model of the Artificial Neuron
Since the last two decades, there has been a continuing interest in developing the neuromorphic circuits and sys- tems that mimic the operation of biological neurons and brains, which enables considerably faster and more energy-efficient emulations of the neurons and neural systems. Due to the computational simplicity of our model, it is rather straightforward to implement the proposed neuron model in hardware, either in digital circuits or analog circuits. There have been several circuit implementations of Izhikevich neuron model and its variants [16] [17] . Thus in our case it is intuitive to add a leaky integrator emulating the axon, as well as the switching devices for selecting one of two sets of 
A conceptual design of the proposed artificial neuron are shown in Figure 4, where the axonal spikes are ori- ginated from the unstable state of the neuron circuit and the artificial neuron is considered as a parameter-de- pendent dynamic system. The parameters of such dynamic system can be stored in non-volatile memory devices. Through modifying the parameter values in the memory, the spiking neuron unit can alter the axonal dynamics between the passive conduction mode and the persistent firing mode.
We have built the neuromorphic model based on the concept design with SPICE and Verilog-A languages, and simulated the model in Synopsys® HSPICE Simulator. The circuit model is shown in Figure 5(a) and Figure 5(b). The soma membrane circuit (Figure 5(a)) essentially implements the Izhikevich neuron model [10] , which includes a SPICE block describing Equations (1)-(2), an adder, a Schmitt trigger and two NMOS transis- tors (M1, M2) as switches. The stimulus 

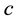
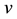

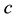

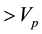



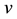
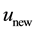

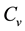

Table 2. Simulation parameters.
Figure 4. Conceptual design of the proposed artificial neuron.

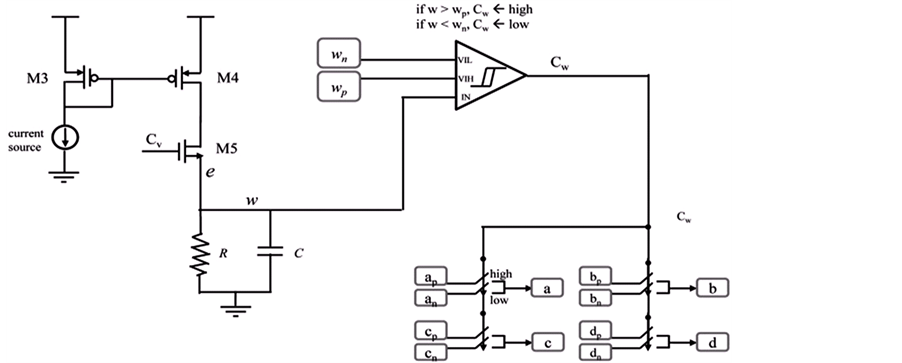
Figure 5. (a) The soma membrane circuit; (b) The axon circuit.
In the axon circuit (Figure 5(b)), a parallel RC circuit implements the axonal leaky integrator. When the soma membrane is generating a spike, 










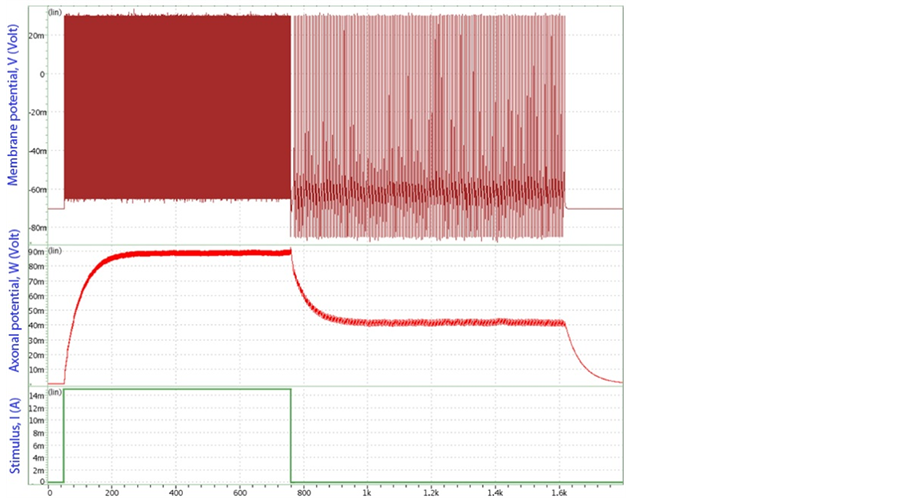
Based on the long-pulse stimulation protocol and the circuit parameters given in Table 3, the simulation re- sults of the circuit are shown in Figure 6. It should be noted that the values of the stimulus current 
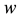
5. Persistent Firing Spiking Network
We have used this model to simulate a spiking network of 1000 randomly connected neurons. The network takes into account of axonal conduction delays [18] and spike-timing-dependent plasticity (STDP), which is consi- dered to be “polychromous” [13] . The network consists of 800 excitatory neurons with regular spiking pattern [11] and 200 inhibitory neurons. As around 80% of EGFP-positive interneurons were found to have persistent firing behavior by repeated somatic current injection [12] , we set in the 80% simulation, or 160 of the inhibitory neurons to be capable of persistent firing while the remaining 20% are fast spiking inhibitory neurons.
Each excitatory neuron is connected to 100 random neurons, and each inhibitory neuron, including persistent firing neuron, is randomly connected to 100 excitatory neurons only. Each synaptic connection has a fixed in- teger conduction delay between 1 ms and 20 ms. The conduction delay in the range of 1 - 20 ms is randomly as-
Table 3. Circuit simulation parameters.
Figure 6. Circuit simulation results of the artificial neuron, showing that after a continuous applied stimulus stops, the slow integration in the axon leads to persistent firing of spikes. Top: the membrane potential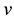



signed to all excitatory synapses, while the 1 ms delay are assigned to all inhibitory synapses [13] . The synaptic connections are modified according to the STDP rule [19] . The implementation of the STDP function is based on Equation (9):
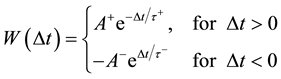
where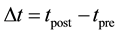


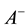
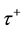
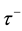
A simplified example of the spiking network structure is illustrated in Figure 7(a). The raster plots of 1-second firing activities in the 1000-neuron spiking network with persistent firing inhibitory interneurons are shown in Figure 7(b). One can see from Figure 7(b) that the network exhibits asynchronous dynamics. Differ- ent rhythmic activities can be identified, ranging from 3 Hz to 8 Hz. Dense vertical columns indicate there are occasional episodes of synchronized firings. As the firing rate of the inhibitory neurons (fast spiking) is higher than that of excitatory neurons (regular spiking), there are generally more firings for inhibitory neurons. The
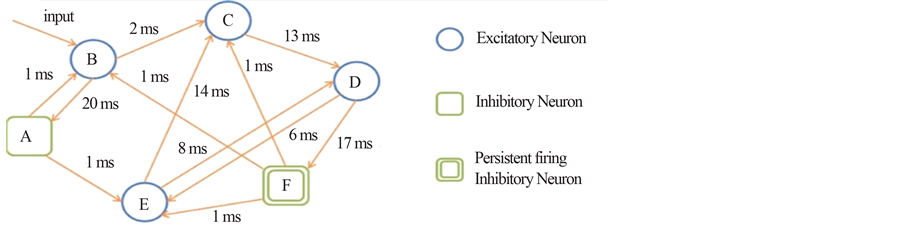

Figure 7. (a) A simplified example of the persistent firing spiking network structure. Among the neurons ranging from A to F in the network, (B, C, D, E) represent the excitatory neurons, and (A, F) represent inhibitory neurons in which F is capable for persistent firing. (b) Raster plots of spike activities in the spiking network of 1000 neurons including persistent firing inhibitory interneurons. Each raster plot shows the 1-second segment of the firing activity. Neurons indexed from 1 to 800 are excitatory neurons, and neurons indexed from 801 to 1000 are inhibitory. Within the 200 inhibitory neurons, there are 160 randomly selected neurons with persistent firing capability. Horizontally continuous dotted lines with neuron index in the range of 801 - 1000 indicate there are persistent firings of action potentials in inhibitory neurons.
persisting firing of inhibitory interneurons in the network, leads to reciprocal inhibition in a longer timescale and thus shut down the activities for a longer period (Figure 7(b) middle column). The synchronization of persis- tent firing interneurons could contribute to the beta and gamma oscillation, whose frequency ranges are close to the persistent firing frequency [20] .
6. Discussion
The possible functions of the persistent firing were suggested to be related to working memory [12] . The ability to maintain the persistent firing of action potentials without on-going stimulation provides a mechanism of stor- ing the information for a short period of time. This mechanism is similar to our working memory [21] -[23] , which actively holds a limited amount of information [24] in the absence of stimuli. Working memory has been extensively explored from perspectives of highly abstract top levels in the domains of psychology, neuroscience and anatomy, but there are much less work from perspectives of bottom level of biological neurons [25] -[30] . It is still unknown how working memory is represented within a population of cortical neurons.
The presented simple model of persistent firing neurons enables further investigation of possible functions of persistent firing, especially the relationship between working memory and persistent firing, and the neural cor- relate of working memory. Recently, we have proposed a model of short term persistent habituation [31] , con- sisting of a persistent firing neuron and a habituating synapse, to explore the presynaptic learning and memory. The interaction of persistent firing axonal and presynaptic processes increases the retention time of the synaptic conductance and therefore the recovery time, and continues the learning of short term habituation for the duration of persistent firing. This leads to a working memory for habituation.
Through incorporating the persistent firing dynamics in spiking networks with axonal delays and STDP learning rules, we can further investigate the interaction of polychronization and persistent neural activities. In the polychronous spiking network, the number of co-existing polychronous groups far exceeds the number of neurons in the network, resulting in an unprecedented memory capacity of the system [13] . Thus it would be in- teresting to investigate how working memory is presented in the polychronous network, and simulate a bio- plausible working memory system with increased memory capacity. To this end, we are working towards the development of artificial cognitive memory with the objective of developing a novel function-driven memory technology in comparison to conventional density-driven storage technology [32] . The models of persistent fir- ing neuron and spiking network presented in this paper can be used in the simulation of cognitive memory ar- chitectures.
Due to the computational simplicity of our model, it is straightforward to implement the model in hardware. We have developed a neuromorphic model of persistent firing neurons [33] , which reproduces the neuronal per- sistent firing behavior by integrating somatic and axonal computational processes of different timescales. Con- sidering there are many existing VLSI implementations of Izhikevich neuron model and its variants [16] [34] - [36] , the proposed neuron model can be conveniently implemented in silicon by incorporating the axonal leaky integrator into the Izhikevich VLSI designs, enabling a considerably faster emulation of the neural systems with persistent neural activity in a highly parallel manner.
7. Conclusion
Based on the recent discovery in neurophysiology which revealed that interneurons can slowly integrate spiking, share the output across a coupled network of axons and respond with persistent firing even in the absence of input to the soma or dendrites, we proposed a new model of persistent firing neuron to bridge the gap between the conventional models and the newly-discovered phenomenon. In this work, we presented and discussed the mathematical and neuromorphic models of the artificial neuron, as well as a persistent firing polychronous spiking network which exhibits asynchronous dynamics. The artificial neuron we proposed, being computationally efficient yet bio-plausible, would be useful to construct and simulate the large scale models of animal or human cortex, which provides a neuromorphic platform for further investigation of the possible functions of persistent firing and their roles in animal and human brain, especially for exploring the relationship between working memory and persistent firing spiking network-based memory and the bio-inspired computer systems.
References
- Lapicque, L. (1907) Recherches quantitatives sur l’excitation electrique des nerfs traitee comme une polarization. Jour- nal of Physiol Pathol Générale, 9, 620-635.
- Sandberg, A. and Bostrom, N. (2008) Whole Brain Emulation: A Roadmap. Future of Humanity Institute, Oxford University, Technical Report #2008-3.
- Hodgkin, A.L. and Huxley, A.F. (1952) A Quantitative Description of Membrane Current and Its Application to Conduction and Excitation in Nerve. The Journal of Physiology, 117, 500-544. http://dx.doi.org/10.1113/jphysiol.1952.sp004764
- Brette, R., Rudolph, M., Carnevale, T., Hines, M., Beeman, D., Bower, J.M., Diesmann, M., Morrison, A., Goodman, P.H., Harris Jr., F.C, et al. (2007) Simulation of Networks of Spiking Neurons: A Review of Tools and Strategies. Journal of Computational Neuroscience, 23, 349-398. http://dx.doi.org/10.1007/s10827-007-0038-6
- Mihalas, S. and Niebur, E. (2009) A Generalized Linear Integrate-and-Fire Neural Model Produces Diverse Spiking Behaviors. Neural Computation, 21, 704-718. http://dx.doi.org/10.1162/neco.2008.12-07-680
- Fitzhugh, R. (1961) Impulses and Physiological States in Theoretical Models of Nerve Membrane. Biophysical Journal, 1, 445-466. http://dx.doi.org/10.1016/S0006-3495(61)86902-6
- Morris, C. and Lecar, H. (1981) Voltage Oscillations in the Barnacle Giant Muscle Fiber. Biophysical Journal, 35, 193-213. http://dx.doi.org/10.1016/S0006-3495(81)84782-0
- Rose, R.M. and Hindmarsh, J.L. (1989) The Assembly of Ionic Currents in a Thalamic Neuron I. The Three-Dimen- sional Model. Proceedings of the Royal Society of London. Series B. Biological Sciences, 237, 267-288. http://dx.doi.org/10.1098/rspb.1989.0049
- Wilson, H.R. (1999) Simplified Dynamics of Human and Mammalian Neocortical Neurons. Journal of Theoretical Biology, 200, 375-388. http://dx.doi.org/10.1006/jtbi.1999.1002
- Izhikevich, E.M. (2001) Resonate-and-Fire Neurons. Neural Networks, 14, 883-894. http://dx.doi.org/10.1016/S0893-6080(01)00078-8
- Izhikevich, E.M. (2003) Simple Model of Spiking Neurons. IEEE Transactions on Neural Networks, 14, 1569-1572. http://dx.doi.org/10.1109/TNN.2003.820440
- Sheffield, M.E.J., Best, T.K., Mensh, B.D., Kath, W.L. and Spruston, N. (2011) Slow Integration Leads to Persistent Action Potential Firing in Distal Axons of Coupled Interneurons. Nature Neuroscience, 14, 200-207. http://dx.doi.org/10.1038/nn.2728
- Izhikevich, E.M. (2006) Polychronization: Computation with Spikes. Neural Computation, 18, 245-282. http://dx.doi.org/10.1162/089976606775093882
- Ning, N., Yi, K.J., Huang, K.J. and Shi, L.P. (2011) Axonal Slow Integration Induced Persistent Firing Neuron Model. Lecture Notes in Computer Science, 7062, 469-476. http://dx.doi.org/10.1007/978-3-642-24955-6_56
- Izhikevich, E.M. (2007) Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting. The MIT Press, Cambridge.
- Wijekoon, J.H. and Dudek, P. (2008) Compact Silicon Neuron Circuit with Spiking and Bursting Behaviour. Neural Networks, 21, 524-534. http://dx.doi.org/10.1016/j.neunet.2007.12.037
- Wijekoon, J.H. and Dudek, P. (2008) Integrated Circuit Implementation of a Cortical Neuron. Proceedings of the IEEE International Symposium on Circuits and Systems, Seattle, 18-21 May 2008, 1784-1787.
- Swadlow, H.A. (1985) Physiological Properties of Individual Cerebral Axons Studied in Vivo for as Long as One Year. Journal of Neurophysiology, 54, 1346-1362.
- Song, S., Miller, K.D. and Abbott, L.F. (2000) Competitive Hebbian Learning through Spike-Timing-Dependent Synaptic Plasticity. Nature Neuroscience, 3, 919-926. http://dx.doi.org/10.1038/78829
- Bartos, M., Vida, I. and Jonas, P. (2007) Synaptic Mechanisms of Synchronized Gamma Oscillations in Inhibitory Interneuron Networks. Nature Reviews Neuroscience, 8, 45-56. http://dx.doi.org/10.1038/nrn2044
- Baddeley, A. (1992) Working Memory. Science, 255, 556-559. http://dx.doi.org/10.1126/science.1736359
- Durstewitz, D., Seamans, J.K. and Sejnowski, T.J. (2000) Neurocomputational Models of Working Memory. Nature Neuroscience, 3, 1184-1191. http://dx.doi.org/10.1038/81460
- Egorov, A.V., Hamam, B.N., Fransen, E., Hasselmo, M.E. and Alonso, A.A. (2002) Graded Persistent Activity in Entorhinal Cortex Neurons. Nature, 420, 173-178. http://dx.doi.org/10.1038/nature01171
- Miller, G.A. (1956) The Magical Number Seven, Plus or Minus Two: Some Limits on Our Capacity for Processing Information. Psychological Review, 63, 81-97. http://dx.doi.org/10.1037/h0043158
- D’Esposito, M., Detre, J.A., Alsop, D.C., Shin, R.K., Atlas, S. and Grossman, M. (1995) The Neural Basis of the Central Executive System of Working Memory. Nature, 378, 279-281. http://dx.doi.org/10.1038/378279a0
- Goldman-Rakic, P.S. (1995) Cellular Basis of Working Memory. Neuron, 14, 477-485. http://dx.doi.org/10.1016/0896-6273(95)90304-6
- Miller, E.K., Erickson, C.A. and Desimone, R. (1996) Neural Mechanisms of Visual Working Memory in Prefrontal Cortex of the Macaque. The Journal of Neuroscience, 16, 5154-5167.
- Amit, D. and Mongillo, G. (2003) Spike-Driven Synaptic Dynamics Generating Working Memory States. Neural Computation, 15, 565-596. http://dx.doi.org/10.1162/089976603321192086
- O’Reilly, R.C. and Frank, M.J. (2006) Making Working Memory Work: A Computational Model of Learning in the Prefrontal Cortex and Basal Ganglia. Neural Computation, 18, 283-328. http://dx.doi.org/10.1162/089976606775093909
- Szatmary, B. and Izhikevich, E.M. (2010) Spike-Timing Theory of Working Memory. PLoS Computational Biology, 6, e1000879. http://dx.doi.org/10.1371/journal.pcbi.1000879
- Ramanathan, K., Ning, N., Dhanasekar, D., Li, G., Shi, L.P. and Vadakkepat, P. (2012) Presynaptic Learning and Me- mory with a Persistent Firing Neuron and a Habituating Synapse: A Model of Short Term Persistent Habituation. International Journal of Neural Systems, 22, Article ID: 1250015. http://dx.doi.org/10.1142/S0129065712500153
- Shi, L.P., Yi, K.J., Ramanathan, K., Zhao, R., Ning, N., Ding, D. and Chong, T.C. (2011) Artificial Cognitive Memory―Changing from Density Driven to Functionality Driven. Applied Physics A, 102, 865-875. http://dx.doi.org/10.1007/s00339-011-6297-0
- Ning, N., Huang, K.J. and Shi, L.P. (2012) Artificial Neuron with Somatic and Axonal Computation Units: Mathematical and Neuromorphic Models of Persistent Firing Neurons. Proceedings of the 2012 International Joint Conference on Neural Networks (IJCNN), Brisbane, 10-15 June 2012, 1-7.
- van Schaik, A., Jin, C., McEwan, A. and Hamilton, T.J. (2010) A Log-Domain Implementation of the Izhikevich Neuron Model. Proceedings of 2010 IEEE International Symposium on Circuits and Systems (ISCAS), Paris, 30 May-2 June 2010, 4253-4256.
- Li, G.Q., Ning, N., Ramanathan, K., Wei, H., Pan, L. and Shi, L.P. (2013) Behind the Magical Numbers: Hierarchical Chunking and the Human Working Memory Capacity. International Journal of Neural Systems, 23, Article ID: 1350019. http://dx.doi.org/10.1142/S0129065713500196
- Li, G.Q., Wen, C.Y., Li, Z.G., Zhang, A.M., Yang, F. and Mao, K.Z. (2013) Model-Based Online Learning with Kernels. IEEE Transactions on Neural Networks and Learning Systems, 24, 356-369. http://dx.doi.org/10.1109/TNNLS.2012.2229293
NOTES
*The authors contribute equally to this work.
This work is funded by Brain Inspired Computing Research, Tsinghua University (20141080934).