International Journal of Intelligence Science
Vol.3 No.1A(2013), Article ID:29547,6 pages DOI:10.4236/ijis.2013.31A006
Missing Values Imputation Based on Iterative Learning
School of Management and Engineering, Nanjing University, Nanjing, China
Email: huaxiongli@nju.edu.cn
Received November 3, 2012; revised January 17, 2013; accepted January 27, 2013
Keywords: Incomplete Data; Missing Values Imputation; Iterative Learning; Intension; Extension
ABSTRACT
Databases for machine learning and data mining often have missing values. How to develop effective method for missing values imputation is an important problem in the field of machine learning and data mining. In this paper, several methods for dealing with missing values in incomplete data are reviewed, and a new method for missing values imputation based on iterative learning is proposed. The proposed method is based on a basic assumption: There exist cause-effect connections among condition attribute values, and the missing values can be induced from known values. In the process of missing values imputation, a part of missing values are filled in at first and converted to known values, which are used for the next step of missing values imputation. The iterative learning process will go on until an incomplete data is entirely converted to a complete data. The paper also presents an example to illustrate the framework of iterative learning for missing values imputation.
1. Introduction
Many data mining and machine learning methods have been well developed based on the assumption that the attribute values of each object in the universe is known [1,2]. However, real-world data often contain missing values either because some values are lost or because the cost of acquiring them are too high. How to properly learning knowledge from such incomplete data has become a crucial problem in the field of machine learning and data mining. It is necessary to develop new methods that can be used to effectively learn rules from incomplete data. Such problem has been widely faced in literature [3-12].
The simplest method to solve this problem is to delete the objects with missing values, then use the rest of the objects as training set to the successive learning process. Such methods may result in the decrease of information for learning. Another similar method is to ignore the objects with missing values in some certain phase of learning. For example in algorithm C4.5 [3], cases with unknown values are ignored while computing the information content, and the information gain for an attribute X is then multiplied by the fraction of cases for which the value of X is known. Although ignoring missing values may be of efficiency when there are not so many missing values, it will be of invalidation when the number of missing values is very large.
Another important category to deal with missing values focus on filling in missing values so that incomplete data can be converted into complete data, which are also called missing values imputation. Such a conversion is conducted before the main process of rule induction, therefore it is a kind of preprocessing. After such preprocessing, those proposed methods for inducing rules from complete data can be used. Among all the methods to fill in missing values, several main approaches are frequently mentioned in literature. The simplest method is to fill in missing values with “most common attribute value”. For example algorithm CN2 [4], proposed by Clark, P. and Niblett, T. in 1989, uses this strategy. A improved version of this method uses “concept most common attribute value” to fill in missing values, i.e., the attribute values selected to filled in missing values are restricted to the same concept [5]. Grzymala-Busse, J. W. proposes “assigning all possible values of the attribute restricted to the given concept” in 1991 [6], which is effective when the number of missing values is not so large. However, it may result in high cost of computation since all possible values are considered when there exist many missing values. Ghahramani, Z. and Jordan, M. I. present a framework based on maximum likelihood density estimation for learning from incomplete data in 1994 [7]. They use mixture models for the density estimates and make two distinct appeals to the Expectation Maximization principle in deriving a learning algorithm. EM is used both for the estimation of mixture components and for coping with missing data. Moreover, in rough set theory, many researchers extend the equivalence relation to other binary relations such as similarity relation, tolerance relation, dominance relation in order to deal with missing values [8-11]. Such extensions are based on certain assumptions: missing values are considered equal to some known values. Thus they can be regarded as another kind method to fill in missing values.
There are still two fundamental important problems in these existing methods for filling in missing methods. One is the gradual use of the known values and the filledin missing values in the whole process. Most methods fill in all missing values before learning, i.e., the filling-in process is one-off finished without considering the use of filled-in values for the next step of filling in other missing values. After filling in some missing values in the universe, information will increase. It is a reasonable strategy to fill in other missing values by the utilization of the filled-in values since the filled-in values bring new available information, and this process can recursively continue until a certain terminate conditions are satisfied.
The other problem is the strategy of filling in missing values. In the existing methods, missing values imputation and learning process are separately treated. There are many missing values imputation methods as well as many learning theories. The connection of these two category processes are not sufficiently discussed. In fact, we may take the missing values imputation problem as a special case of learning process. The missing values can be regarded as a learning target, and the data with known values present a train data sets. Therefore, we may establish the connections between the missing values imputation and learning process. Many learning theories can be introduce to missing values imputation, which presents a new view on missing values imputation. The objective of this paper is to propose a new framework for missing values imputation by introducing gradually iterative learning approach.
2. Learning-Based Missing Values Imputation
Traditionally, filling in missing values is usually considered as a technique method to fix up the original data for rule induction. For an information table, condition attributes and decision attributes are treated distinctly as different kinds of attributes according to their different roles in the rule induction. It is assumed that there exist some certain relationship between the condition attribute values and decision attribute values. Such relationship can be denoted as a rule:
if (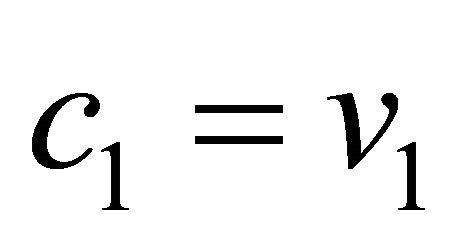 and
and  and
and  and
and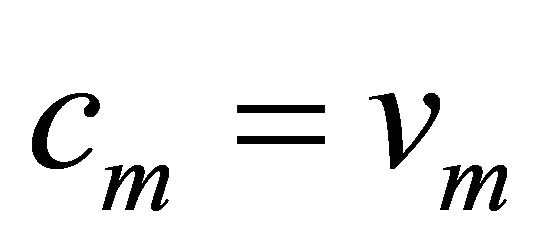 ) then
) then 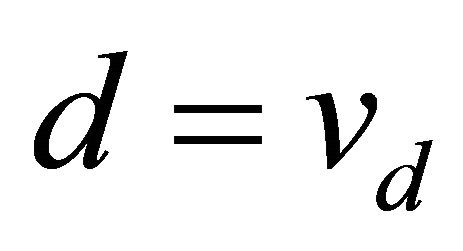 where
where  are condition attributes,
are condition attributes, 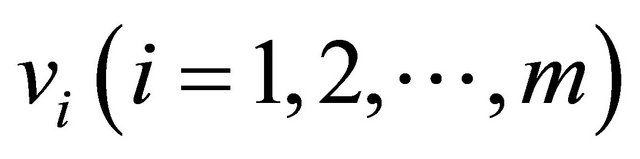 are values of condition attributes, and
are values of condition attributes, and 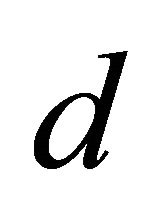 is decision attribute,
is decision attribute,  is the value of decision attribute. A main task of machine learning and data mining is to find out such rules that can properly express the relationship between condition attribute values and decision attribute values. As incomplete data is concerned, rule induction is difficult to fulfill since some attribute values are missing. By filling in missing values with some certain approaches, rule induction may be easily fulfilled as incomplete data have been converted to complete data.
is the value of decision attribute. A main task of machine learning and data mining is to find out such rules that can properly express the relationship between condition attribute values and decision attribute values. As incomplete data is concerned, rule induction is difficult to fulfill since some attribute values are missing. By filling in missing values with some certain approaches, rule induction may be easily fulfilled as incomplete data have been converted to complete data.
From another perspective, filling in missing values can also be concerned as a learning process if we treat missing values as a special unknown decision output that need to learn from the known values. The goal of this kind of learning is to induce rules for filling in missing values. Suppose 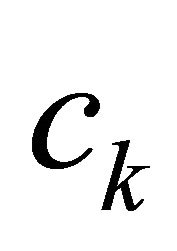 is an attribute with missing values, we may consider filling in missing values of
is an attribute with missing values, we may consider filling in missing values of 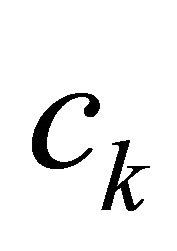 as a process of learning such a set of rules as:
as a process of learning such a set of rules as:
if (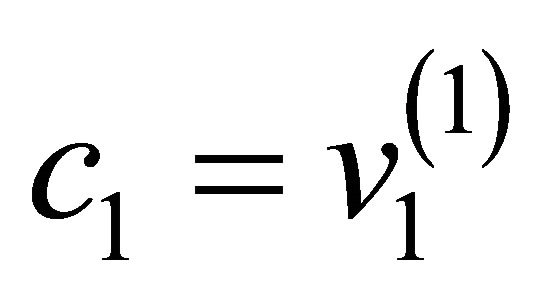 and
and 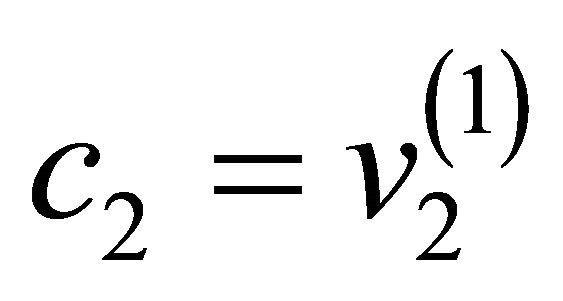 and
and  and
and 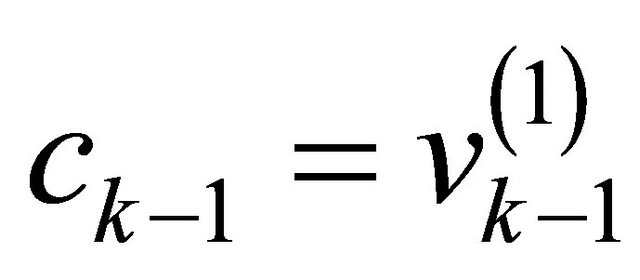 and
and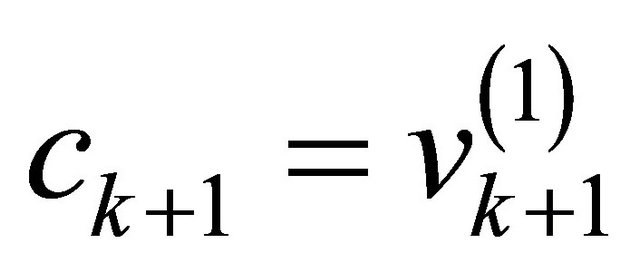 ) and
) and  and
and 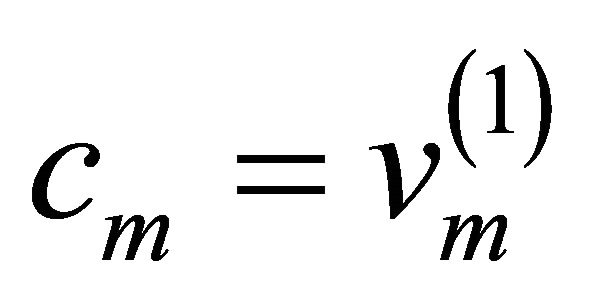 then
then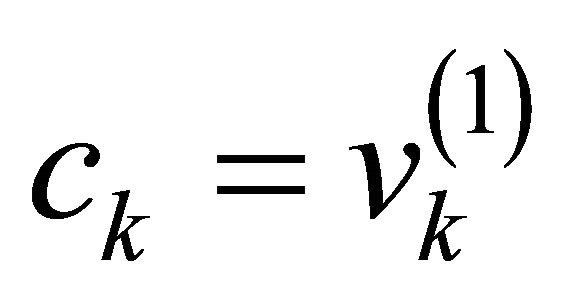 if (
if (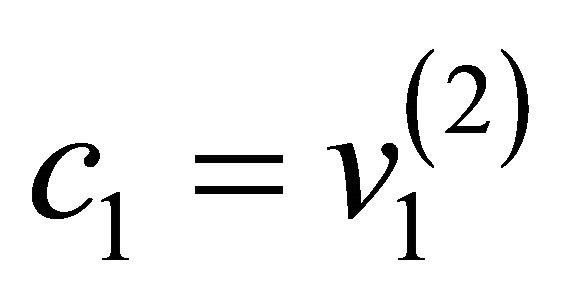 and
and 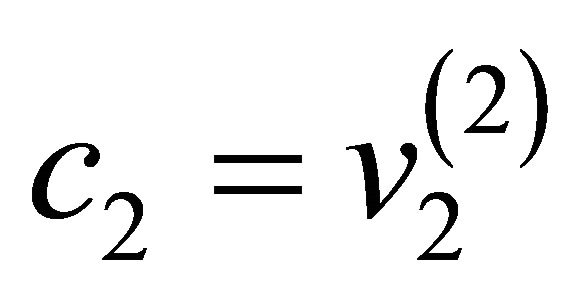 and
and  and
and 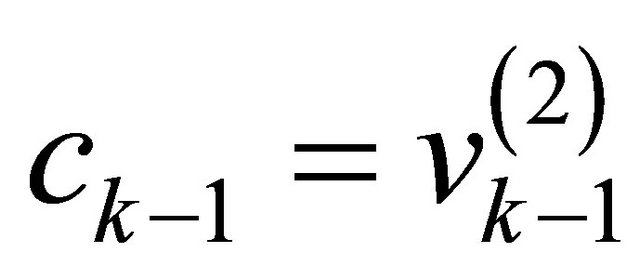 and
and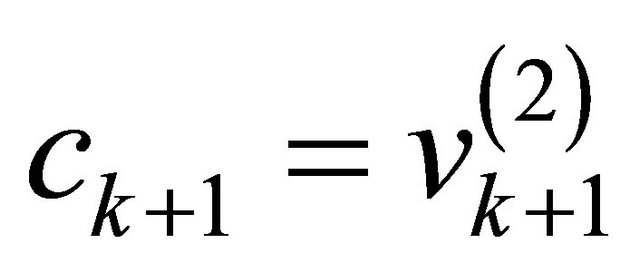 ) and
) and  and
and 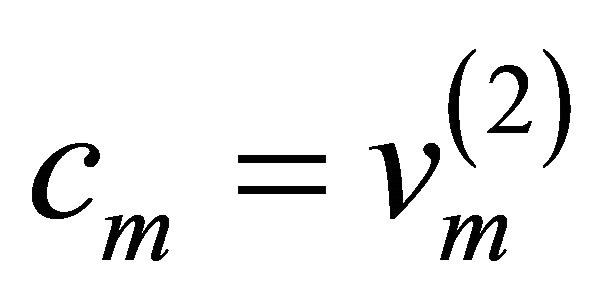 then
then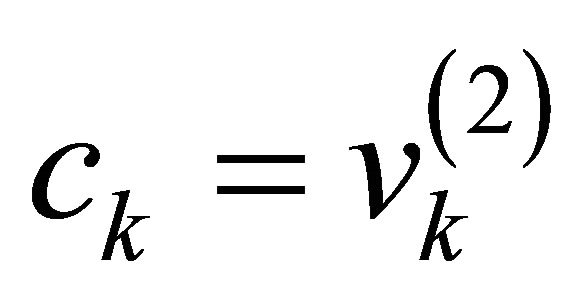 ,
, 
if (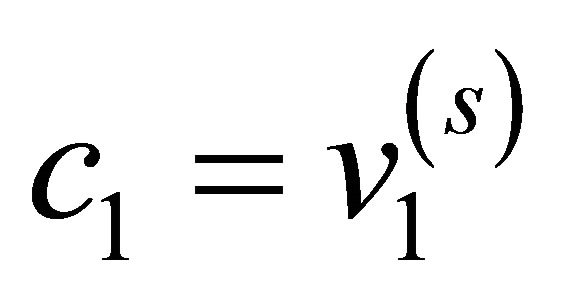 and
and 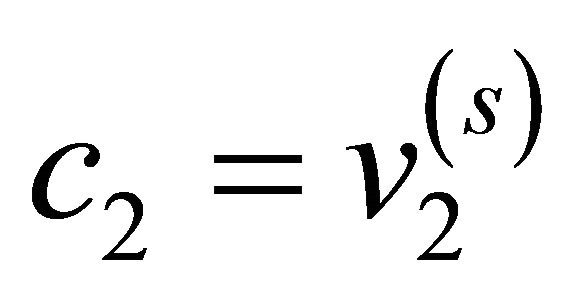 and
and  and
and 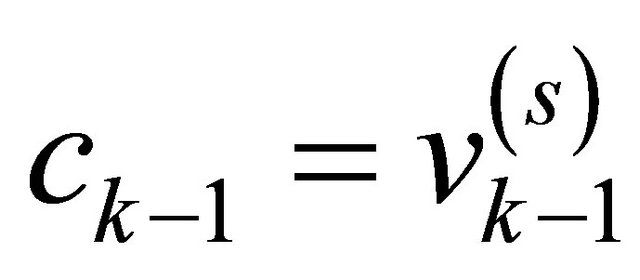 and
and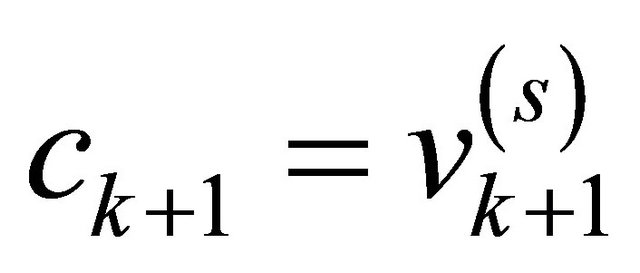 ) and
) and  and
and 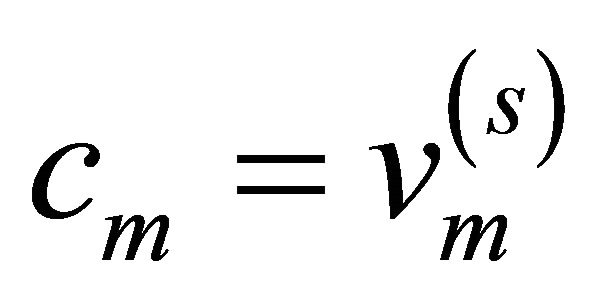 then
then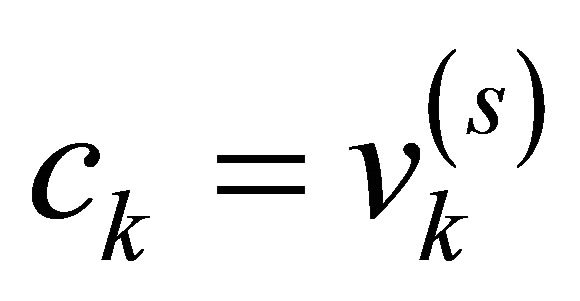 .
.
It is a reasonable assumption that there may exist some connections among condition attribute values. Such a viewpoint provide us a new learning-oriented understanding on filling in missing values. Many appropriate methods of machine learning can be used. In next section, we will propose a gradual iterative learning method for filling in missing values.
3. Iterative Learning for Missing Values Imputation
Many psychologist believe that the cognitive process of human being is a gradual learning process. At the beginning of learning process, those simple elementary knowledge is acquired at first, which is the foundation of the next step learning. With the accumulating of elementary knowledge, cognitive ability may get stronger so that more complex concept may be learnt in the next step of learning process. Such a gradually iterative learning process of human being can be used in filling in missing values. At the beginning of filling in missing values, there may be only few missing values that can be filled in with high confidence since initially there often exist many missing values and the usable information is scarce. After a partial process of filling in missing values, some missing values have been converted to known values since they have been filled in with some certain values, thus known values increase and add more usable information, which may be available for the next step of filling in remained missing values. Based on the refined data, some missing values that can not be certainly filled in previously may get more confidence on some certain values. This reiteration will go on so that an incomplete data may be gradually converted to complete data.
Such iterative learning approach is similar to some other existing learning methods such as semi-supervised learning, a machine learning technique proposed by Shahshahani and Landgrebe [13]. Semi-supervised learning focus on learning from both labeled and unlabeled data— a small amount of labeled data with a large amount of unlabeled data. It falls between unsupervised learning and supervised learning. Many machine learning researchers have found that unlabeled data, when used in conjunction with a small amount of labeled data, can produce considerable improvement in learning accuracy. With iteratively labeling those unlabeled objects according to refined data, the performance of learning continually increases.
By using iterative learning method, we propose a new learning approach of filling in missing values. The main idea can be described as follows. At the beginning of the learning process, some of missing values are filled in based on learning from existing known values, thus the number of known values increase and the remained missing values can be filled in by learning from the refined set of known values. This process will go on until a certain condition is satisfied.
A high-level algorithm for filling in missing values using iterative learning approach is proposed as follows:
Input: an information table 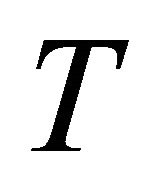 with known values set
with known values set 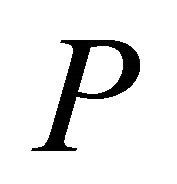 and missing values set
and missing values set 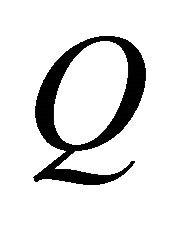
Output: a refined information table 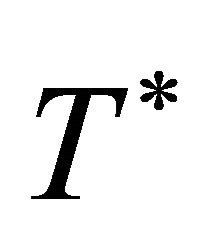 with known values set
with known values set  and missing values set
and missing values set 
Set 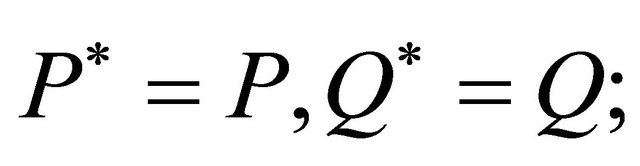
Repeat the following operations Select a subset  of
of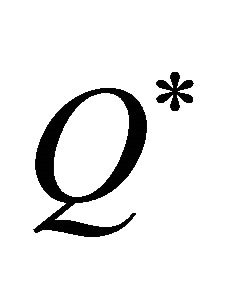 ;
;
Fill in 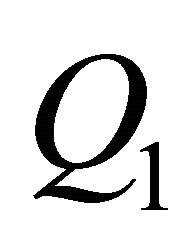 based on learning from
based on learning from ;
;
Replace 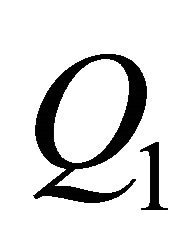 by filled-in values set
by filled-in values set ;
;
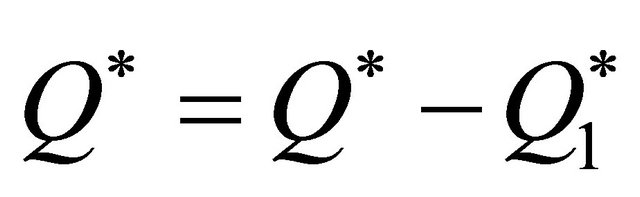 ;
;
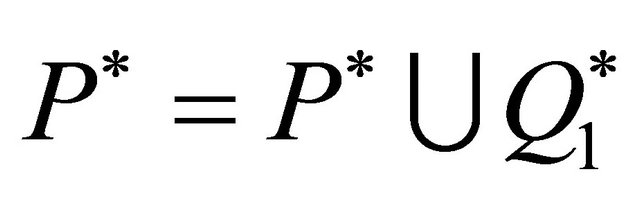 ;
;
Until a termination condition is satisfied Return 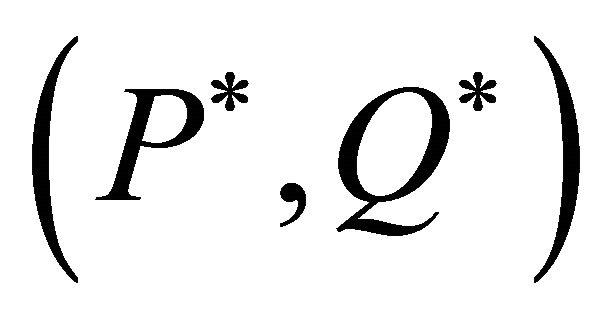
In the high-level algorithm mentioned above, known values set and missing values set will be refined in each of many learning iterations. The key point of this algorithm is to decide the strategy of filling in missing values:
Select a subset 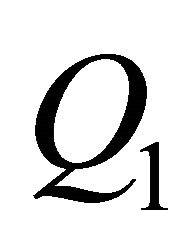 of
of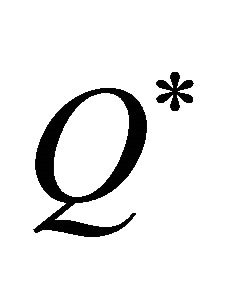 ;
;
Fill in 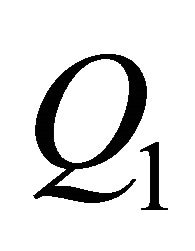 based on learning from
based on learning from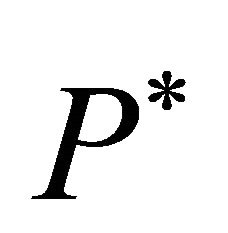 ;
;
Many methods of machine learning can be used. Here we adopt concept formation and learning as a solution.
4. Concept Formation in Incomplete Information Table
In general, a concept can be defined by a pair of intension and extension, where the intension of a concept is given by a set of properties and the extension of a concept normally defined with respect to a particular set of examples [14-17]. Considering a complete information table such as Table 1 [14], we may express the conception as this pattern.
Let 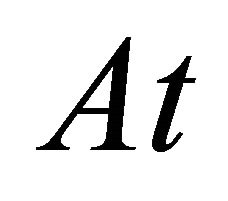 be a finite set of attributes or features. For each attribute
be a finite set of attributes or features. For each attribute , we associate it with a set of values or labels
, we associate it with a set of values or labels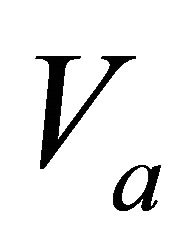 . Let
. Let 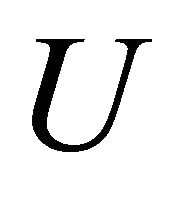 be a set of universe whose elements are called objects. For each
be a set of universe whose elements are called objects. For each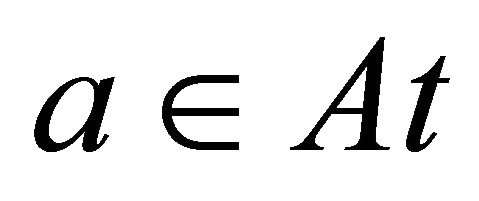 , there is a mapping
, there is a mapping 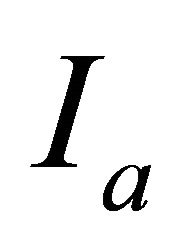 connecting elements of
connecting elements of 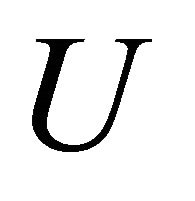 and elements of
and elements of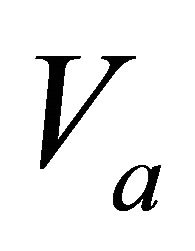 , and the value of an object
, and the value of an object 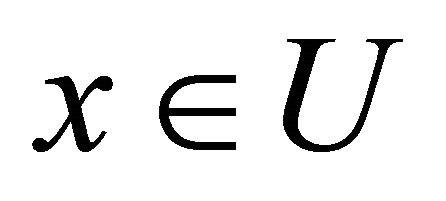 on an attribute
on an attribute 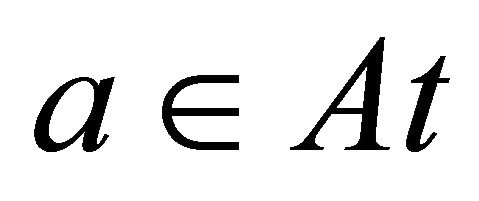 is denoted by
is denoted by . Commonly in complete information table, where the attribute values of each object are known, it is assumed that the mapping
. Commonly in complete information table, where the attribute values of each object are known, it is assumed that the mapping 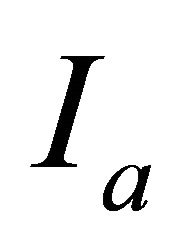 is single-valued.
is single-valued.
For an incomplete information table, there exist objects whose attribute values are multiple-valued or unknown. In this case, the value of an object 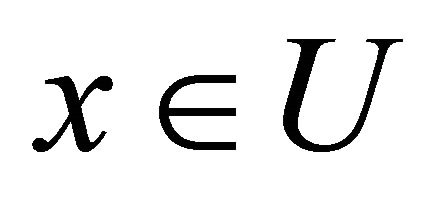 on an attribute
on an attribute 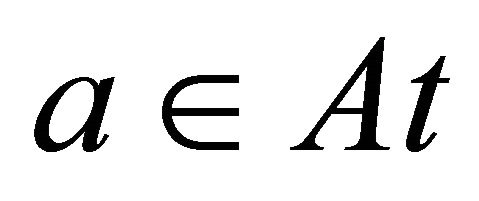 i.e.
i.e.  can be expressed by *, namely
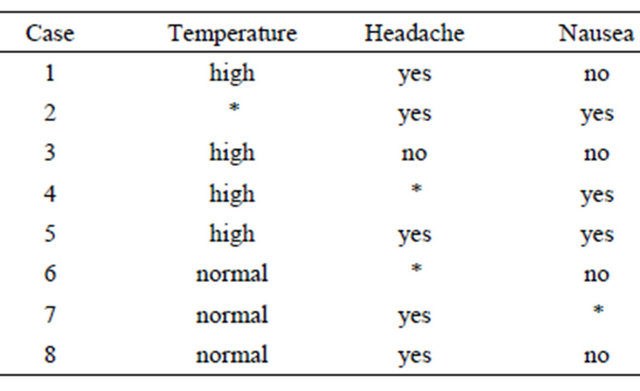
can be expressed by *, namely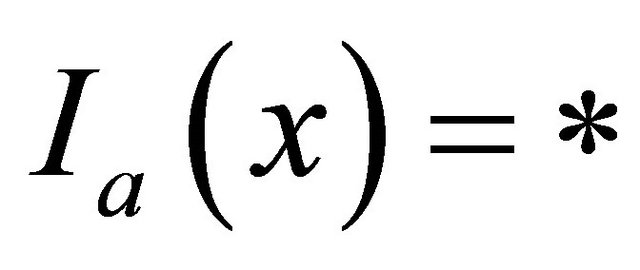 . An example of an incomplete table is presented in Table 2.
. An example of an incomplete table is presented in Table 2.
Table 1. An complete information table.
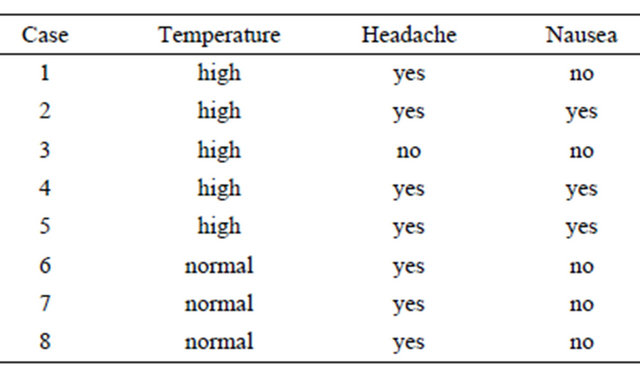
Table 2. Original incomplete information table.
In this paper, we adopt the decision logic language 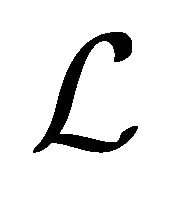 used and studied by Pawlak to formally define intensions of concepts [14]. In an incomplete information system, an atomic formula is given by
used and studied by Pawlak to formally define intensions of concepts [14]. In an incomplete information system, an atomic formula is given by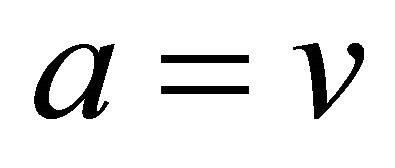 , where
, where , and it should be stressed that the unknown attribute value (null value) i.e. “*” is not included in
, and it should be stressed that the unknown attribute value (null value) i.e. “*” is not included in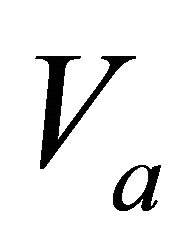 . Therefore, in an atomic formula,
. Therefore, in an atomic formula, 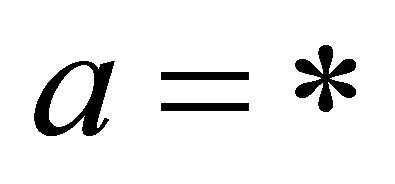 is illegal. For each atomic formula
is illegal. For each atomic formula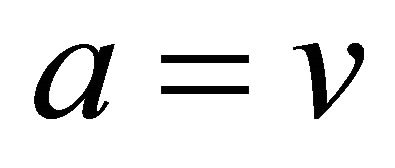 , an object
, an object 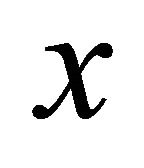 satisfies it if
satisfies it if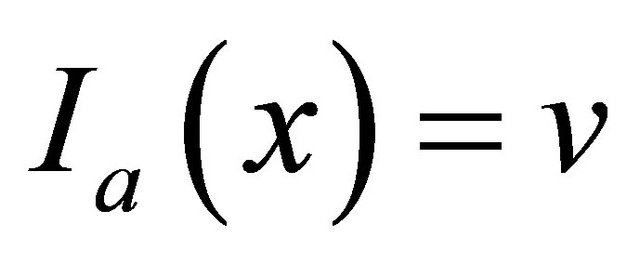 , written
, written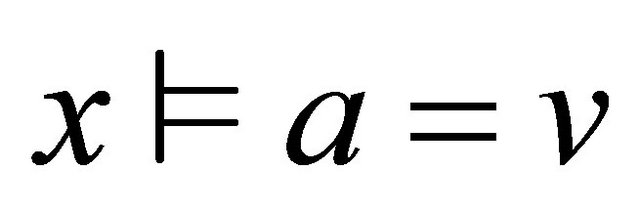 . Otherwise, it does not satisfy
. Otherwise, it does not satisfy 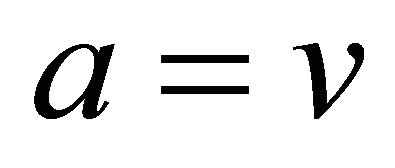 or
or 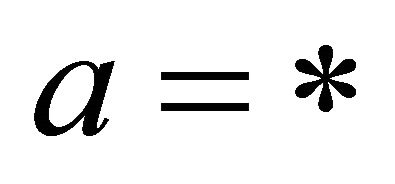 and is written
and is written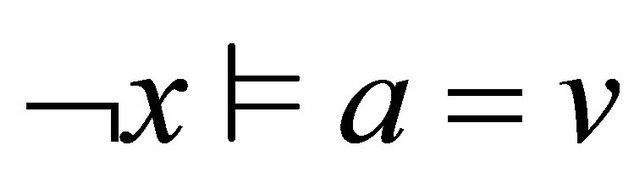 . From atomic formulas, we can construct other formulas by applying the logic connectives
. From atomic formulas, we can construct other formulas by applying the logic connectives 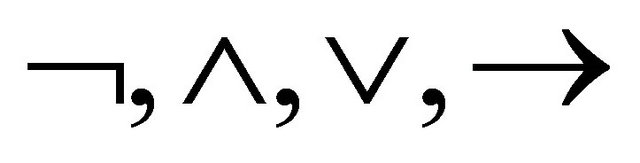 and
and . The satisfiability of any formula is defined as follows:
. The satisfiability of any formula is defined as follows:
1) 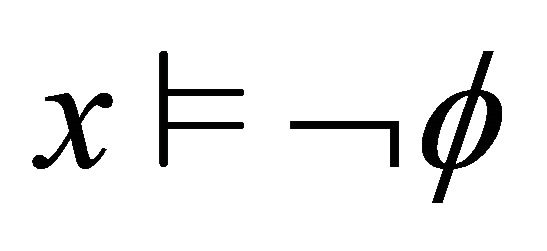 iff not
iff not 2)
2)  iff
iff 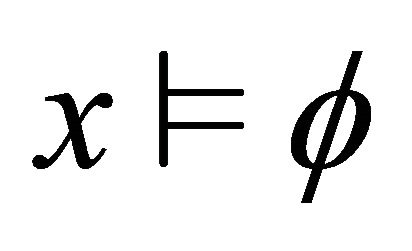 and
and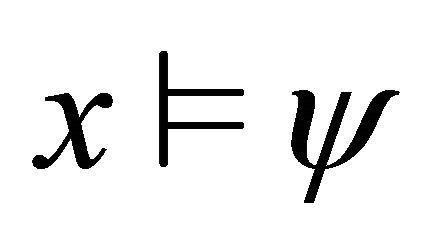 3)
3)  iff
iff 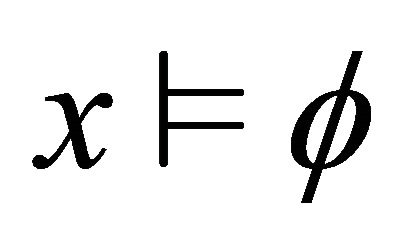 or
or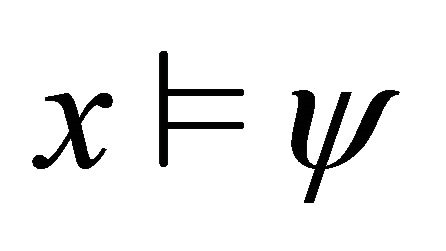 4)
4) 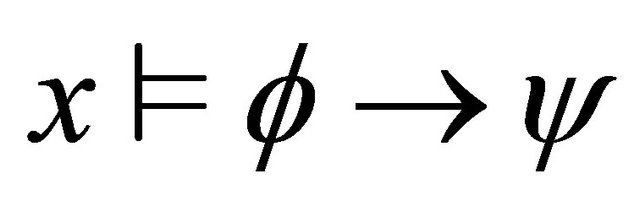 iff
iff 5)
5)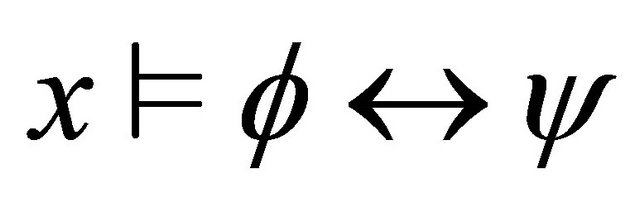 . iff
. iff 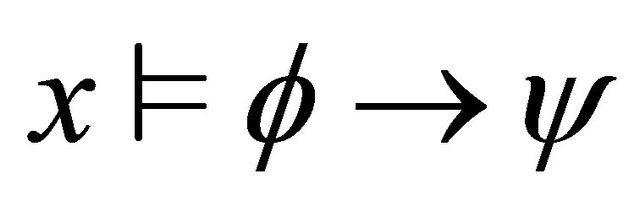 and
and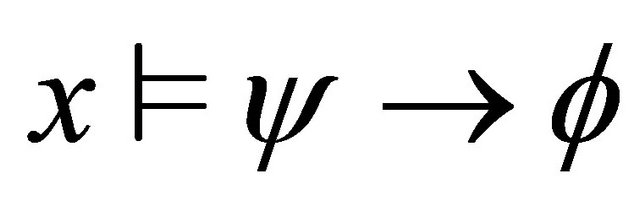 .
.
Traditionally, a basic formula 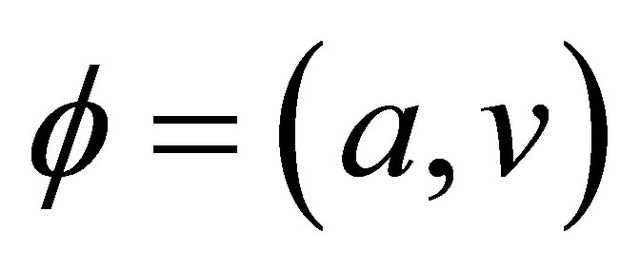 can represent a intension of a concept, and the extension of the concept can be represented by the elements which satisfy the formula, denoted by
can represent a intension of a concept, and the extension of the concept can be represented by the elements which satisfy the formula, denoted by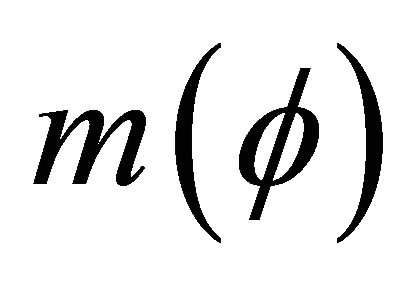 . When considering the missing attribute values, all elements with the value of the attribute
. When considering the missing attribute values, all elements with the value of the attribute  is are not included. Namely,
is are not included. Namely, 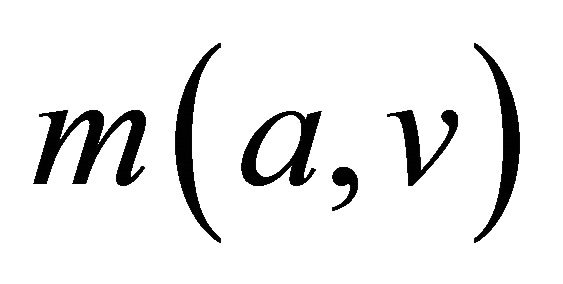 only contains the elements whose value of attribute
only contains the elements whose value of attribute  is exactly
is exactly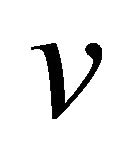 . In Table 2, for example:
. In Table 2, for example:
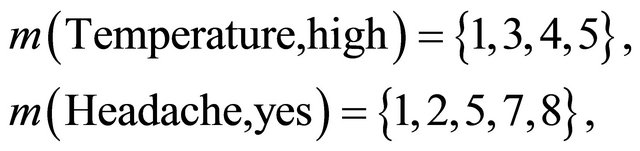
Moreover, following results can be got by applying the logic connectives:

5. Iterative Imputation Using Concept Formation
Let us take Table 2 as an example to describe the process of iterative learning for filling in missing values using concept formation. Suppose we’ll learn the rules for filling in missing values of attribute  at first. Training set used to learn such rules for filling in missing values of attribute
at first. Training set used to learn such rules for filling in missing values of attribute 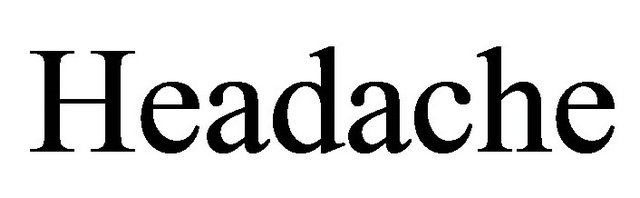 is restricted to
is restricted to 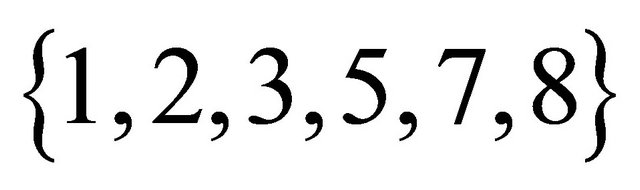 . Then we list all related concepts:
. Then we list all related concepts:
We can find  and
and
 thus a set of rules is inducted as:
thus a set of rules is inducted as:

then we fill in  and
and  with
with . Therefore information table has been converted to Table 3.
. Therefore information table has been converted to Table 3.
We’ll use the refined data to learn rule for filling in missing values of attribute  in the next step. Training set for learning is restricted to
in the next step. Training set for learning is restricted to . By using the similar approach mentioned above, we can find
. By using the similar approach mentioned above, we can find
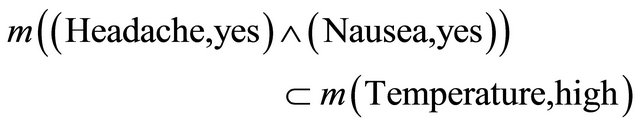
and the corresponding rule is:
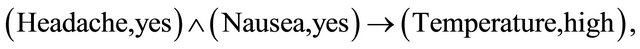
then  is filled in with
is filled in with . Therefore the information table is converted to Table 4.
. Therefore the information table is converted to Table 4.
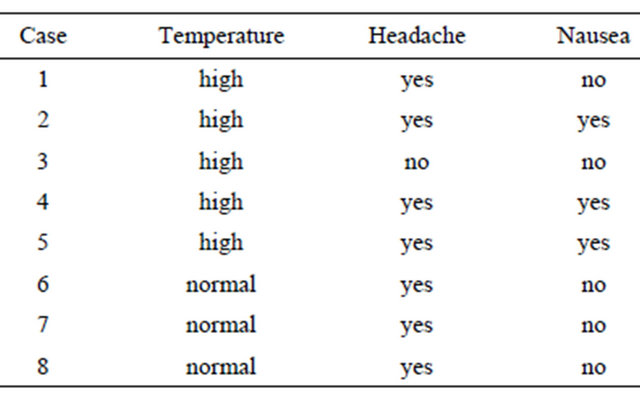
Similarly,  can be filled in with
can be filled in with 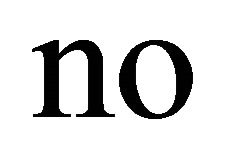 on the basis of
on the basis of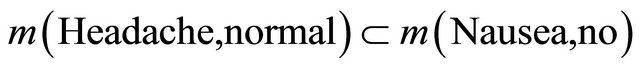 , i.e.,
, i.e.,
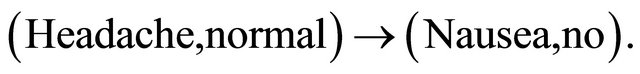
Table 3. Missing values imputation: Headache.
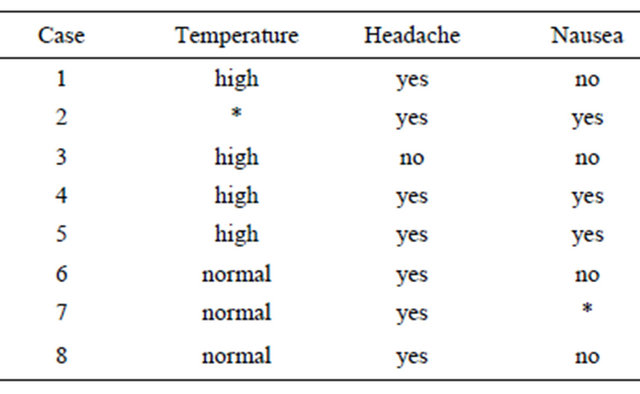
Table 4. Missing values imputation: Temperature.

Table 5 presents the final repaired data. We may find that the incomplete data has been converted to a complete data after four-step filling in missing values based on iterative learning, then the complete information table can be used for traditional rule induction based on any exist learning methods.
Remark: In the process of iterative learning for missing values imputation, the selection order of the missing values for imputation is a fundamental problem, which affects the final imputation result. In order to present a high quality imputation result, we should fill in the missing values with the highest confidence in each phase of imputation, that is, we prefer to fill in the missing values associated with a higher confidence rule, which leads to a more reliable imputation result.
It is a basic assumption that there exist some certain relationship among the different attributes. Therefore, in the missing values imputation process, the iterative learning method is used to discover the connection between the known values and the missing values. It should be noted that many machine learning approaches besides concept learning can also be used to discover the relationship between the known values and missing values. In the future work, we will further study on the missing values select order for imputation and present detailed experimental analysis on the proposed method. In addition, many other machine learning methods for iterative missing values imputation will be further investigated in the future work.
Table 5. Missing values imputation: Nausea.
6. Conclusion
In this paper, several methods for dealing with missing values in incomplete data are reviewed, and a new method for missing values imputation based on iterative learning is proposed. At the beginning of missing values imputation, there may be only few missing values that can be filled in with high confidence. After some missing values are filled in, they are converted to known values, then known values increase and more usable information is introduced, which may be available for the next step of missing values imputation. Based on the refined data, some missing values that can not be certainly filled in previously may get more confidence on some certain values. This reiteration will go on so that an incomplete data may be gradually converted to complete data. The paper present a theoretic framework of missing values imputation as well as a practical solution.
7. Acknowledgements
This research is supported by the National Natural Science Foundation of China (71201076), and the Natural Science Foundation of Jiangsu, China (BK2011564).
REFERENCES
- T. M. Mitchell, “Generalization as Search,” Artificial Intelligence, Vol. 18, No. 2, 1982, pp. 203-226. doi:10.1016/0004-3702(82)90040-6
- T. M. Mitchell, “Machine Learning,” McGraw-Hill, New York, 1997.
- J. R. Quinlan, “C4.5: Programs for Machine Learning,” Morgan Kaufmann, San Mateo, 1993.
- P. Clark and T. Niblett, “The CN2 Induction Algorithm,” Machine Learning, Vol. 3, No. 4, 1989, pp. 261-283. doi:10.1007/BF00116835
- J. W. Grzymala-Busse and W. J. Grzymala-Busse, “An Experimental Comparison of Three Rough Set Approaches to Missing Attribute Values,” In: J. Peters, A. Skowron, I. Duntsch, J. Grzymala-Busse, E. Orlowska and L. Polkowski, Eds. LNCS Transactions on Rough Sets VI, Springer, Berlin, 2007, pp. 31-50.
- J. W. Grzymala-Busse, “On the Unknown Attribute Values in Learning from Examples,” In: Z. Ras and M. Zemankova, Eds., Proceedings of 6th International Symposium on Methodologies for Intelligent Systems, Springer, Berlin, 1991, pp. 368-377.
- Z. Ghahramani and M. I. Jordan, “Supervised Learning from Incomplete Data via an EM Approach,” In: J. D. Cowan, G. Tesauro and J. Alspector, Eds., Advances in Neural Information Processing Systems, Morgan Kaufmann, San Mateo, 1994, pp. 120-127.
- S. Greco, B. Matarazzo and R. Slowinski, “Handling Missing Values in Rough Set Analysis of Multi-Attribute and Multi-Criteria Decision Problems,” In: N. Zhong, A. Skowron and S. Ohsuga, Eds., Proceedings of 7th International Workshop on Rough Sets, Fuzzy Sets, Data Mining, and Granular-Soft Computing, Springer, Berlin, 1999, pp. 146-157.
- M. Kryszkiewicz, “Rough Set Approach to Incomplete Information Systems,” Information Sciences, Vol. 112, No. 1-4, 1998, pp. 39-49. doi:10.1016/S0020-0255(98)10019-1
- M. Kryszkiewicz, “Rules in Incomplete Information Systems,” Information Sciences, Vol. 113, No. 3-4, 1999, pp. 271-292. doi:10.1016/S0020-0255(98)10065-8
- J. Stefanowski and A. Tsoukiàs, “On the Extension of Rough Sets under Incomplete Information,” International Journal of Intelligent System, Vol. 16, No. 1, 2000, pp. 29-38.
- H. X. Li, Y. Y. Yao, X. Z. Zhou and B. Huang, “TwoPhase Rule Induction from Incomplete Data,” In: G. Wang, T. Li, J. Grzymala-Busse, D. Miao, A. Skowron and Y. Yao, Eds., Proceedings of 3rd International Conference on Rough Sets and Knowledge Technology, Springer, Berlin, pp. 47-54.
- B. Shahshahani and D. Landgrebe, “The Effect of Unlabeled Samples in Reducing the Small Sample Size Problem and Mitigating the Hughes Phenomenon,” IEEE Transactions on Geoscience and Remote Sensing, Vol. 32, No. 5, 1994, pp. 1087-1095. doi:10.1109/36.312897
- Y. Y. Yao, “Concept Formation and Learning: A Cognitive Informatics Perspective,” In: C. Chan, W. Kinsner, Y. Wang and D. Miller, Eds., Proceedings of 3rd IEEE International Conference on Cognitive Informatics, IEEE CS Press, New York, 2004, pp. 42-51.
- Y. Y. Yao and N. Zhong, “An Analysis of Quantitative Measures Associated with Rules,” In: X. Wu, K. Ramamohanarao and K. Korb, Eds., Proceedings of 2nd Pacific-Asia Conference on Knowledge Discovery and Data Mining, Springer, Berlin, 1999, pp. 479-488.
- Y. Zhao, Y. Y. Yao and J. T. Yao, “Level-Wise Construction of Decision Trees for Classification,” International Journal of Software Engineering and Knowledge Engineering, Vol. 16, No. 1, 2006, pp. 103-123. doi:10.1142/S0218194006002690
- J. T. Yao and Y. Y. Yao, “Induction of Classification Rules by Granular Computing,” In: J. Alpigini, J. Peters, A. Skowron and N. Zhong, Eds., Proceedings of 3rd International Conference on Rough Sets and Current Trends in Computing, Springer, Berlin, 2002, pp. 331-338. doi:10.1007/3-540-45813-1_43

