Open Journal of Modern Hydrology
Vol.06 No.03(2016), Article ID:69340,14 pages
10.4236/ojmh.2016.63014
Assessing the Performance of Two Hydrologic Models for Forecasting Daily Streamflows in the Cazones River Basin (Mexico)
Fernando González-Leiva1, Rodrigo Valdés-Pineda2*, Juan B. Valdés2, Laura A. Ibáñez-Castillo2
1Posgrado en Ingeniería Agrícola y Uso Integral del Agua, Universidad Autónoma Chapingo, Chapingo, México
2Department of Hydrology and Water Resources, University of Arizona, Tucson, AZ, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 May 2016; accepted 26 July 2016; published 29 July 2016
ABSTRACT
Floods have caused significant human and economic losses in the Cazones River Basin, located on the Gulf of Mexico. Despite this knowledge, steps towards the design and implementation of an early warning system for the Cazones are still a pending task. In this study we contributed by establishing a hydrological scheme for forecasting mean daily discharges in the Cazones Basin. For these purposes, we calibrated, validated and compared the HyMod model (HM) which is physics-based, and an autoregressive-based model coupled with the Discrete Kalman Filter (ARX-DKF). The ability of both models to accurately predict discharges proved satisfactory results during the validation period with RMSEHYMOD = 2.77 [mm/day]; and RMSEARX-DKF = [2.38 mm/day]. Further analysis based on a Streamflow Assimilation Ratio (SAR) revealed that both models underestimate the discharges in a similar proportion. This evaluation also showed that, under the most common conditions, the simpler stochastic model (ARX-DKF) performs better; however, under extreme hydrological conditions the deterministic HM model reveals a better performance. These results are discussed under the context of future applications and additional requirements needed to implement an early warning hydrologic system for the Cazones Basin.
Keywords:
Hydrologic Models, Cazones Basin, HyMod, Discrete Kalman Filter, Hydrologic Uncertainty

1. Introduction
The interaction between global warming and natural variability affects the magnitude and frequency of extreme hydrological events, i.e. droughts and floods [1] - [3] . Future hydroclimatic scenarios associated with these impacts are influenced by numerous sources of uncertainty, motivating the scientific community to work on better forecasting of hydrological events [4] . Hydrological modeling techniques are an essential tool for the development of efficient water governance schemes of various types i.e., hydraulic works management, mitigation of natural disasters, and risk management, among others [4] - [11] .
In Mexico, communities around river basins within humid-subtropical climates could especially benefit from accurate hydrological modeling. These humid-subtropical climates result from the interaction between several ocean-atmosphere teleconnections, i.e., the El Niño Southern Oscillation (ENSO), the Pacific Decadal Oscillation (PDO), the Arctic Oscillation (AO), the North Atlantic Oscillation (NAO), and the Atlantic Multidecadal Oscillation (NAO). These ocean-atmosphere interactions generate flooding and landslides that can result in important socio-economic losses, particularly in the floodplains of the basins.
To mitigate the impacts associated to these extreme events, during 2002 the Mexican government established an Early Warning System for Tropical Cyclones (EWSTC), which is the main tool used to monitor the intensity, trajectory and distance of the cyclones. The information generated by EWSTC is then used by federal and state agencies who take supportive measures. Despite this centralized system has demonstrated to be effective for early warning of meteorological disasters, the role of local agencies is still pending in terms of expanding the “hydrological knowledge” about it e.g. calibration and validation of hydrologic models that deal with specific physical characteristics of the basins or those sustained in new algorithms of data assimilation.
In order to advance towards the development of an early warning hydrological system for the Cazones Basin, in this study we have established a first approximation for forecasting mean daily discharges in the basin. For these purposes, we calibrated, validated, and compared two lumped hydrological models The first model is HyMod (HM), a physics-based model that accounts for all components of the water balance [12] - [16] . The second is an autoregressive-based model coupled with the Discrete Kalman Filter (ARX-DKF); the latter is considered as the optimal sequential data assimilation method for linear dynamics and measurement processes with Gaussian error statistics [17] - [21] . In the following sections of this paper we describe the study area and dataset, the calibration and validation steps for both models, and the discussion and conclusions concerning the results of our study.
2. Methods
2.1. Study Area
The Cazones River Basin is located between the coordinates 20˚18' and 21˚15'N and 97˚17' and 98˚32'W, in the Hydrological Region N˚27 North, called Veracruz Tuxpan-Nautla [22] [23] . The mean annual flow of the Cazones River is 54 m3/s, but for a single day this value can reach a maximum of about 1250 m3/s [24] . The river has a total drainage area of approximately 2688 km2 distributed in three states of Mexico (Figure 1(a)): Puebla (56%), Hidalgo (13.5%), and Veracruz (30.5%) [25] . For this study we considered the Poza Rica stream gauge as the outlet of the basin (Figure 1(b)), accounting for a total area of 1,605 km2. Grasslands and agricultural fields represent more than 70% of the total land area of the basin (Figure 1(c)). The average slope of the basin is about 27% (Figure 1(d)), and the highest elevation is about 2880 m.a.s.l. (Figure 1(e)). The maximum height of the main channel is about 2,100 m.a.s.l. These geomorphological characteristics translate into an estimated time of concentration of about 16 hours [25] [26] .
2.2. Hydroclimatology of the Cazones Basin
Much of Mexico has a monsoon climate, with a rainy season during the summer months (JJA) and a relatively dry winter season (DJF) [27] . Climate anomalies in Mexico depend mostly on the interaction between ENSO, PDO, AO, NAO, and AMO [28] - [33] . In the positive phase of the El Niño phenomenon (i.e., a warmer Equatorial Pacific Ocean), the winter is humid throughout Mexico, whereas during the summer, conditions are dry in the north and humid in the south [31] . A humid-subtropical climate dominates the Cazones River Basin, with an average annual temperature of 24˚C and an average annual rainfall of ~1500 mm [34] . This precipitation accumulation is associated with frontal systems during winter, and extreme meteorological events such as tropical storms or hurricanes that form in the Atlantic over the Gulf of Mexico during the summer [29] [30] [35] [36] .
Figure 1. (a) Cazones River Basin; (b) rain gauges and Poza Rica stream gauge; (c) land use in the basin; (d) slope map of the basin; (e) digital elevation map (30 meters) of the basin.
2.3. Socio-Economic Issues in the Cazones Basin
The Cazones Basin drains over its west-facing slopes. The drainage enters the lowlands around the town of Poza Rica in the state of Veracruz, an important petroleum production area. Extreme meteorological events affecting the area cause high runoff over the saturated soils of the basin, resulting in significant damage [25] [26] [34] [37] . A review of the history of the state of Veracruz reveals extensive human losses due to flooding and landslides. For instance, in October 1999 a tropical depression associated with a polar front produced a 50-year flooding event that affected more than 200,000 inhabitants and caused more than $150 million (US) in economic losses [38] . In 2005, four tropical storms affected about 1.5 million people, and 130,000 houses were damaged by flooding [33] . During 2010, two hurricanes in the same month, Karl (September 17-18) and Mathew (September 26-27,) caused flooding in different parts of the State and economic losses of over $5 billion (US) [33] - [39] . During the last 41 years, flooding in Veracruz has demonstrated a significant positive exponential trend (r = 0.81) (see Figure 2), which can be attributed to climate change (due to global warming), other anthropogenic factors, and natural variability [39] [40] .
2.4. Hydrologic Modeling Using HM and ARX-DKF
Daily streamflow forecasting in the Cazones Basin was conducted using two lumped models (one physics-based and one systems-based). In the definition of HM model we considered the formal steps of model building as stated by [41] i.e., the general model formulation (conceptual model) was performed defining the state variables; the model fluxes; and the adjustable and derived parameters. For the ARX model, we defined the exogenous inputs and the rainfall-runoff transfer function component (see i.e. [42] - [44] ). This model was then coupled with a Discrete Kalman Filter, following the steps outlined by [17] [45] - [48] .
2.4.1. Forcing Data
The input forcing data used in this study include daily, spatially aggregated rainfall amounts (2008-2011) obtained from a total of nine raingauges, mean daily flows obtained from Poza Rica stream gauge (Table 1), and
Figure 2. Annual precipitation obtained from the Poza Rica rain gauge and the number of flood events per year in the Cazones Basin for the period 1970-2011. Source: Flood occurrence data was obtained from DesInventar (2015).
Table 1. Rain and stream gauges used in this study. The code in the first column indicates the gauges as numbered in Figure 1(b). Source: Clicom database [50] .
potential evapotranspiration (PET) calculated using Hargreaves Method [49] . These records were obtained from the database CLICOM (Climate Computerized) administered by the National Meteorological Service of Mexico [50] . Mean daily streamflows from the Cazones Basin were obtained from the BANDAS database [51] and then used in the calibration and validation schemes.
2.4.2. Conceptual Representation (Process Model)
The physical or mathematical principles governing the entire behavior of the hydrologic system were summarized for each model through the use of simple conceptual Directed Graphs (DG), which are an explicit representation of the major processes occurring within the hydrological system, their structural organization, and their results [41] . Because the HM is a physics-based model (see e.g., [12] [14] [16] [52] , the major physical processes leading to the behavior of the hydrologic system were defined in order to clearly describe the dynamics by which the state variables change over time [41] . The HM conceptualizes the basin as a simple, nonlinear soil moisture reservoir connected with two series of linear reservoirs for channeling excess rainfall, two or three identical quick-flow tanks (depending on the calibration scheme applied) representing short-term surface detention, and one, slow-flow tank representing groundwater storage (Figure 3(a)).
On the other hand, physical conditions are not considered in the formulation of the ARX-DKF model, which is intended to find the best mathematical or causal relation(s) between the input and the output of the hydrological system [46] [53] - [55] . This coupled model is based on an autoregressive component (ARX) for the streamflow, in which rainfall is considered the exogenous input. This component is then merged with the Discrete Kalman Filter (DKF) algorithm, following the steps described by [17] [48] [56] - [58] . The resulting model is then used to forecast the mean daily stream flow records (Figure 3(b)).
2.4.3. System Parametrization
This stage consisted of developing a group of hypotheses regarding the mathematical forms of the process equations that are believed to describe the physical processes linking the subsystem components (see i.e. [41] [59] ). We used the HM as a conceptual non-distributed (lumped) hydrological model with six parameters (see Table 2) accounting for all subcomponents of the water balance ( [12] [16] [60] ). The ARX-DKF model contains time- varying parameters (i.e., they evolve over time) obtained from the autoregressive component, which are then used in the Kalman implementation (Table 2). The autoregressive characteristics of the streamflow records allow for the development of a matrix of parameters that are used to forecast streamflow [55] .
Figure 3. Simple conceptual directed graphs for the (a) HM and (b) ARX-DKF models.
Table 2. Parametrization of HM and ARX-DKF models.
2.4.4. Computational Model, Calibration, and Validation
The computational implementation of both models was coded using a MatlabTM routine, which was packaged in a toolbox1 format to facilitate usage. From the historical records of mean daily streamflows, the year 2008 was selected to calibrate the initial parameters of both models, because it contained the largest number of flood events (see Figure 2). The Mean Squared Error (MSE), Root Mean Squared Error (RMSE), and Nash-Sutcliffe Efficiency (NSE) [61] [62] were used as error measures for both the calibration and validation schemes (Table 3). The parameters of HM were calibrated from 2008 records using the Shuffle Complex Evolution Algorithm (SCE-UA) [63] - [65] . Since the parameters of the ARX-DKF model are time-varying, they were initially calibrated using 2008 records, and then updated using 2009-2010 records (see Figure 3(b)). For these purposes we used an autoregressive component (ARX) taking into account the principles of parsimony [66] - [68] . To ensure consistent analysis, both models were validated using the 2009-2011 period. During this validation, the performance of each model was further evaluated by calculating a Streamflow Assimilation Ratio Index (SAR) which is proposed in this study. This index shows the relationship between modeled (QMod) and observed (QObs)
streamflows for each day i under analysis . In this study, SAR was used for measuring the
. In this study, SAR was used for measuring the
predictive capacity of each model; however, it can also be used to apply bias correction schemes in a similar way of that performed over Global or Regional Climate Models (GCMs or RCMs); that is, by calculating an av-
eraged version of SAR (averaged Bias Correction Factor) over all n days under analysis: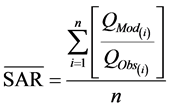 , and then using this factor to correct raw data resulting from hydrological models.
, and then using this factor to correct raw data resulting from hydrological models.
3. Results and Discussion
3.1. Sensitivity Analysis and Calibration of Parameters
For the HM model the selection of the final set of parameters from the 2008 calibration was used to define the physical processes associated with hydrological responses in the Cazones Basin. For instance, the MSEHM obtained fell as low as 8.79 mm, and all the parameters converged after completing the optimization scheme (Figure 4). For example, the calibrated maximum storage capacity in the basin was found to be about 39.4 mm, which may be considered a small capacity given the humid-subtropical characteristics of the Basin and the wide range of capacity (5 - 600 mm) used to calibrate the 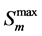 parameter. Additionally, as denoted by the α-para- meter, the surface runoff in the basin is partitioned in slightly dissimilar proportions between the surface (53%) and the subsurface component (47%) revealing a higher runoff component compared to infiltration rates. In fact,
parameter. Additionally, as denoted by the α-para- meter, the surface runoff in the basin is partitioned in slightly dissimilar proportions between the surface (53%) and the subsurface component (47%) revealing a higher runoff component compared to infiltration rates. In fact,
Table 3. Forecasting performance measures used in this study.
Figure 4. Evolution of parameters and objective function (MSE) by applying the SCE-UA optimization scheme during 2008. The evolution scheme was applied using five complexes and 25 loops at each complex (for details see: [63] [64] [73] .
the land use in the basin which is dominated by grasslands and agricultural fields (>70%) must play a significant role in modulating the hydraulic properties and consequently the infiltration capacity of soils. For instance, some studies have found that grasslands have lower (higher) infiltration (runoff) rates than forests [69] .
For the ARX-DKF model the best set of parameters α and β calculated during the calibration period and then used to predict daily streamflows was identified when we combined the streamflow of the previous day (Qt-1) and the rainfall that occurred in the prior two days (Pt-2). This means that the largest autocorrelation of the observed streamflows is achieved at lag t − 1 (days), and the largest cross-correlation between rainfall and observed streamflows is achieved at lag t − 2 (days). Similar findings have been reported by [70] - [72] .
3.2. Classical Validation of Models
During the validation period, the performance of the chosen parameters was tested, revealing that both models are able to satisfactorily reproduce the mean daily discharges in the Basin. In fact, the forecasting performance of both models was improved during the validation period as evaluated through error measures. The MSEHM was about 35% larger than MSEARX-DKF and these results were also consistent when looking at RMSE and NSE measures (Table 4). The relationship between modeled and observed discharges shows significant correlations: 0.88 for HM and 0.90 for ARX-DKF (Figure 5); however, as indicated by the slight deviation of the least squares line (LSL) from the 1:1 line, the predicted discharges from both models tend to slightly underestimate the observed discharges. In general, all previous findings suggest, at least at this stage, that ARX-DKF time- variable parametrization performs better than HM parametrization.
3.3. Streamflow Assimilation Ratio (SAR)
A significant relationship between SARHM and SARARX-DKF (r = 0.68) revealed interesting additional details about the performance of the models (in a validation period of 982 days). For instance, the joint distribution of SAR revealed four different regions (Figure 6(a)) that allow further evaluation of their performance. The Overestimation (Underestimation) Region is the one in which both models overestimate (underestimate) the observed discharges. In the Mixed Region, one model overestimates while the other underestimates or vice versa. The analysis of the Overestimation Region denoted similar performance by both models (Figure 6(b)). However, when the Underestimation Region was analyzed, ARX-DKF performed better than HM (Figure 6(c)): in about 76% of the days in the validation period, the latter model underestimated the observed discharges, with an average relationship represented by . In contrast, the ARX-DKF model underestimated the discharges in only about 66% of the days in the validation period, with an average relationship represented by
. In contrast, the ARX-DKF model underestimated the discharges in only about 66% of the days in the validation period, with an average relationship represented by
Figure 5. Linear relationships between predicted and observed streamflows in the Cazones Basin.
Figure 6. (a) Scatter plot between the SAR calculated for both HM and ARX-DKF models; (b) distribution of the Overestimation Region of both models; (c) Distribution of the Underestimation Region of both models.
Table 4. Error measurement results obtained for the validation period (2009-2011).
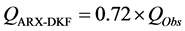 . Focusing on the ability of the models to predict extreme conditions, we found that HM performs slightly better than ARX-DKF when predicting large discharge values: the average relationship between predicted and observed discharges (>20 mm/day) for each model is represented by
. Focusing on the ability of the models to predict extreme conditions, we found that HM performs slightly better than ARX-DKF when predicting large discharge values: the average relationship between predicted and observed discharges (>20 mm/day) for each model is represented by 

3.4. Hydrological Uncertainty
Judging from the hydrographs of both models (Figure 7), the predicted discharges can realistically forecast the mean daily discharges. The uncertainty bands calculated through a Monte Carlo approach (i.e., bootstrapping of errors) can be satisfactorily used to minimize both models’ risk of inaccuracy. However, during extreme flooding events―i.e. an event in 2011 that resulted in an historic peak of ~1250 m3/s (~67.2 mm/day) on July 17th (Figure 7)―the uncertainty bands can be not able to explain the observed discharge; this can be partially attributed to the fact that point-based rainfall cannot account for the spatial distribution of rainfall in the entire basin. Therefore, as a way of improving the confidence of the predictions and reduce the hydrological uncertainty, the design of an early warning hydrological system will additionally require the validation of combined new satellite-based precipitation products (gridded datasets) and lumped or distributed models.
3.5. Discussion
The use of predictions from the centralized EWSTC allows for the generation of pre-alert scenarios with larger lead time; however, this scheme does not contain information about the states of the hydrological system i.e. it cannot be used to determine possible damages of hydraulic infrastructure. This is the most important pending task of local agencies as a way to expand the hydrological knowledge of EWSTC. This knowledge will have to develop new early warning hydrological systems dedicated to represent hydrological response based on the intrinsic characteristics of the Basins or dependent on new algorithms of data assimilation. In this study we contributed to establish a hydrological scheme for forecasting mean daily discharges in the Cazones Basin. For in- stance, based on classical validation schemes and the application of SAR, we determined that under normal con-
Figure 7. Observed and simulated mean daily river discharge [mm] for the 2009-2011 validation period at the Poza Rica stream gauge in the Cazones River Basin. The shaded areas represent 95% uncertainty levels (confidence intervals) obtained from Monte Carlo resampling (1000 samples) of the absolute errors of prediction under the assumption that they are normally distributed. When the lower boundaries reached negative values, they were adjusted to be 20% of the modeled discharge.
ditions ARX-DKF model performs slightly better than HM; however, this latter model performs better under extreme conditions. These hydrological statements and the information generated from both models can be used to warn the emergency coordinators in a different way than that currently offered by EWSTC, and thus are of great value to pre-manage a probable hydraulic emergency. An additional and important component of this validation process will be based on the coordination between public agencies, decision-makers, and stakeholders, and how these members make use of these tools and the information generated by the models to define appropriate policies towards the development of early warning hydrological systems at catchment scale i.e. temporal resolution of interest, selection of models, and ranges of applicability.
4. Conclusion
This study evaluated two lumped hydrological models to contribute in advancing towards the development of an early warning hydrologic system in the Cazones River Basin. HM and ARX-DKF were calibrated, validated, and compared to determine the best modeling system for forecasting mean daily discharges in the basin. The results from error measures and SAR revealed that the performance of the autoregressive-based ARX-DKF model (less underestimation) was slightly better than the performance of the physics-based HM model (greater underestimation). Despite these differences, under extreme hydrological conditions HM performs slightly better than ARX-DKF. The implementation of SAR proposed for this study showed to be a practical alternative to evaluate and compare the performance of hydrological models, and it seems to be promising for applying bias correction schemes over raw predictions obtained from hydrological models. The application of these methods is aimed to improve the predictions and reduce the uncertainty of hydrological models of course future studies will have to deal with the validation RCMs for the basin i.e. precipitation estimates provided by real-time satellite-based products as CMORPH, PERSSIANN or TMPA, combined with different lumped and spatially distributed hydrological models i.e. SACRAMENTO, HYMOD, HBV, TOMODEL, among others. The success or failure of these tools and the use of the information they provide will continue being a challenge since hydrologists have to also deal with climate models outputs coming with an additional source of uncertainty; therefore, the level of coordination attained between national agencies, decision-makers and stakeholders, in developing policies aimed to adequately implement new early warning systems including maybe not all but several scenarios of uncertainty, will play a central role for improving water governance schemes at catchment scale.
Acknowledgements
The authors of this study greatly appreciate to Consejo Nacional de Ciencia y Tecnología (CONACyt); and the NASA-USAID SERVIR Program (Award 11-SERVIR11-58) for their support in the realization of this study.
Cite this paper
Fernando González-Leiva,Rodrigo Valdés-Pineda,Juan B. Valdés,Laura A. Ibáñez-Castillo, (2016) Assessing the Performance of Two Hydrologic Models for Forecasting Daily Streamflows in the Cazones River Basin (Mexico). Open Journal of Modern Hydrology,06,168-181. doi: 10.4236/ojmh.2016.63014
References
- 1. Trenberth, K. (2005) Uncertainty in Hurricanes and Global Warming. Science (Washington), 308, 1753-1754.
http://dx.doi.org/10.1126/science.1112551 - 2. WMO (2009) WMO Report No 168. Guide to Hydrological Practices Volume II: Management of Water Resources and Application of Hydrological Practices. World Meteorological Organization, Geneva.
- 3. IPCC (2014) Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (Core Writing Team: Pachauri, R.K. and Meyer, L.A., Eds.). IPCC, Geneva, 151 pp.
- 4. Todini, E. (2007) Hydrological Catchment Modelling: Past, Present and Future. Hydrology and Earth System Sciences, 11, 468-482.
http://dx.doi.org/10.5194/hess-11-468-2007 - 5. Chavasse, D.I. and López, S.S. (1997) Asociación determinístico-estocástica para predicción de caudales. Ingeniería del agua, 4, 55-64.
http://dx.doi.org/10.4995/ia.1997.2723 - 6. Pizarro-Tapia, R., Valdés-Pineda, R., Olivares, C. and González, P.A. (2014) Development of Upstream Data-Input Models to Estimate Downstream Peak Flow in Two Mediterranean River Basins of Chile. Open Journal of Modern Hydrology, 4, 132.
http://dx.doi.org/10.4236/ojmh.2014.44013 - 7. Valdés-Pineda, R., Pizarro, R., García-Chevesich, P., Valdés, J.B., Olivares, C., Vera, M., Balocchi, F., Pérez, F., Vallejos, C., Fuentes, R. and Abarza, A. (2014) Water Governance in Chile: Availability, Management and Climate Change. Journal of Hydrology, 519, 2538-2567.
http://dx.doi.org/10.1016/j.jhydrol.2014.04.016 - 8. Sood, A. and Smakhtin, V. (2015) Global Hydrological Models: A Review. Hydrological Sciences Journal, 60, 549-565.
http://dx.doi.org/10.1080/02626667.2014.950580 - 9. Salvadore, E., Bronders, J. and Batelaan, O. (2015) Hydrological Modelling of Urbanized Catchments: A Review and Future Directions. Journal of Hydrology, 529, 62-81.
http://dx.doi.org/10.1016/j.jhydrol.2015.06.028 - 10. Devia, G.K., Ganasri, B.P. and Dwarakish, G.S. (2015) A Review on Hydrological Models. Aquatic Procedia, 4, 1001-1007.
http://dx.doi.org/10.1016/j.aqpro.2015.02.126 - 11. Eden, S., Megdal, S.B., Shamir, E., Chief, K. and Mott Lacroix, K. (2016) Opening the Black Box: Using a Hydrological Model to Link Stakeholder Engagement with Groundwater Management. Water, 8, 216.
http://dx.doi.org/10.3390/w8050216 - 12. Moore, R.J. (1985) The Probability-Distributed Principle and Runoff Production at Point and Basin Scales. Hydrological Sciences Journal, 30, 273-297.
http://dx.doi.org/10.1080/02626668509490989 - 13. Vrugt, J.A., Diks, C.G., Gupta, H.V., Bouten, W. and Verstraten, J.M. (2005) Improved Treatment of Uncertainty in Hydrologic Modeling: Combining the Strengths of Global Optimization and Data Assimilation. Water Resources Research, 41, 1-17.
http://dx.doi.org/10.1029/2004WR003059 - 14. Gharari, S., Hrachowitz, M., Fenicia, F. and Savenije, H.G. (2013) An Approach to Identify Time Consistent Model Parameters: Sub-Period Calibration. Hydrology and Earth System Sciences, 17, 149-161.
http://dx.doi.org/10.5194/hess-17-149-2013 - 15. Remesan, R., Bellerby, T. and Frostick, L. (2014) Hydrological Modelling Using Data from Monthly GCMs in a Regional Catchment. Hydrological Processes, 28, 3241-3263.
http://dx.doi.org/10.1002/hyp.9872 - 16. Quan, Z., Teng, J., Sun, W., Cheng, T. and Zhang, J. (2015) Evaluation of the HYMOD Model for Rainfall-Runoff Simulation Using the GLUE Method. Proceedings of the International Association of Hydrological Sciences, 368, 180- 185.
http://dx.doi.org/10.5194/piahs-368-180-2015 - 17. Kalman, R.E. (1960) A New Approach to Linear Filtering and Prediction Problems. Journal of Fluids Engineering, 82, 35-45.
http://dx.doi.org/10.1115/1.3662552 - 18. Reichle, R.H., McLaughlin, D.B. and Entekhabi, D. (2002) Hydrologic Data Assimilation with the Ensemble Kalman Filter. Monthly Weather Review, 130, 103-114.
http://dx.doi.org/10.1175/1520-0493(2002)130<0103:HDAWTE>2.0.CO;2 - 19. Evensen, G. (2003) The Ensemble Kalman Filter: Theoretical Formulation and Practical Implementation. Ocean Dynamics, 53, 343-367.
http://dx.doi.org/10.1007/s10236-003-0036-9 - 20. Evensen, G. (2009) Data Assimilation: The Ensemble Kalman Filter. 2nd Edition, Springer Science & Business Media, Berlin, 307 p.
http://dx.doi.org/10.1007/978-3-642-03711-5 - 21. Rasmussen, J., Madsen, H., Jensen, K.H. and Refsgaard, J.C. (2015) Data Assimilation in Integrated Hydrological Modeling Using Ensemble Kalman Filtering: Evaluating the Effect of Ensemble Size and Localization on Filter Performance. Hydrology and Earth System Sciences Discussions, 12, 2267-2304.
http://dx.doi.org/10.5194/hessd-12-2267-2015 - 22. INEGI (1984) Anuario Estadístico del Estado de Veracruz. Instituto Nacional de Estadística y Geografía, México, 589 p.
- 23. CONAGUA (2013) Estadísticas del agua en México edición 2013. Comisión Nacional del Agua de México, 165 p.
- 24. CONAGUA (2013) Mapa hidrológico. Escala 1: 1,000,000. Sistema de Información Geográfica del Agua. Subgerencia de programación regional Golfo Centro, Comisión Nacional del Agua de México.
- 25. INEGI (2005) Síntesis de información geográfica del Estado de Veracruz. Instituto Nacional de Estadística y Geografía, México.
- 26. Pereyra, D. and Pérez, J.A. (2005) Hidrología de superficie y precipitaciones intensas 2005 en el estado de Veracruz. In: Tejeda Martínez, A. and Welsh Rodriguez, C., Eds., Inundaciones 2005 en el estado de Veracruz, Universidad Veracruzana, Consejo Veracruzano de Ciencia y Tecnología, Xalapa, 81-99.
- 27. Magana, V., Amador, J.A. and Medina, S. (1999) The Midsummer Drought over Mexico and Central America. Journal of Climate, 12, 1577-1588.
http://dx.doi.org/10.1175/1520-0442(1999)012<1577:TMDOMA>2.0.CO;2 - 28. Magana, V., Pérez, J.L., Conde, C., Gay, C. and Medina, S. (1997) El fenómeno de El Nino y la Oscilación del Sur (ENOS) y sus impactos en México. Report INE-Oct 97.
- 29. Magana, V.O., Vázquez, J.L., Pérez, J.L. and Pérez, J.B. (2003) Impact of El Nino onprecipitation in Mexico. Geofísica Internacional, 42, 313-330.
- 30. Pavia, E.G., Graef, F. and Reyes, J. (2006) PDO-ENSO Effects in the Climate of Mexico. Journal of Climate, 19, 6433-6438.
http://dx.doi.org/10.1175/JCLI4045.1 - 31. Seager, R., Tzanova, A. and Nakamura, J. (2009) Drought in the Southeastern United States: Causes, Variability over the Last Millennium, and the Potential for Future Hydroclimate Change. Journal of Climate, 22, 5021-5045.
http://dx.doi.org/10.1175/2009JCLI2683.1 - 32. Méndez, M. and Magana, V. (2010) Regional Aspects of Prolonged Meteorological Droughts over Mexico and Central America. Journal of Climate, 23, 1175-1188.
http://dx.doi.org/10.1175/2009JCLI3080.1 - 33. Tejada-Martínez, A. (2010) Inundaciones 2010 en el estado de Veracruz. Consejo Veracruzano de Investigación Científica y Desarrollo Tecnológica, México, 578 p.
- 34. Gutiérrez, E.S., Dávila-Vázquez, G., de Anda Sánchez, J. and Torres, J.D. (2013) Estimación del balance hídrico mediante variables climáticas, en la cuenca del río Cazones, Veracruz, México. Ambiente & água, 8, 104-117.
- 35. Amador, J.A. and Magana, V. (2000) The Low-Level Jet and Convective Activity in the Caribbean. 24th Conference on Hurricanes and Tropical Meteorology. Ft. Lauderdale, 29 May-2 June 2000, 114-115.
- 36. Englehart, P.J. and Douglas, A.V. (2002) Mexico’s Summer Rainfall Patterns: An Analysis of Regional Modes and Changes in Their Teleconnectivity. Atmósfera, 15, 147-164.
- 37. Barcelata, H. (2012) Poza Rica, Economía local y problemática social-Los municipios de Veracruz Vol. III. Primera edición, Universidad de Málaga, 102 p.
- 38. Aguirre, B. and Macías, J. (2006) Las inundaciones de 1999 en Veracruz y el paradigma de la vulnerabilidad. Revista Mexicana de Sociología, 68, 209-230.
- 39. DesInventar (2015) Disaster Information Management System Database.
http://www.desinventar.org/en/ - 40. Magana, V., Zermeno, D. and Neri, C. (2012) Climate Change Scenarios and Potential Impacts on Water Availability in Northern Mexico. Climate Research, 51, 171-184.
http://dx.doi.org/10.3354/cr01080 - 41. Gupta, H.V. and Nearing, G.S. (2014) Debates—The Future of Hydrological Sciences: A (Common) Path Forward? Using Models and Data to Learn: A Systems Theoretic Perspective on the Future of Hydrological Science. Water Resources Research, 50, 5351-5359.
http://dx.doi.org/10.1002/2013WR015096 - 42. Awwad, H.M., Valdés, J.B. and Restrepo, P.J. (1994) Streamflow Forecasting for Han River Basin, Korea. Journal of Water Resources Planning and Management, 120, 651-673.
http://dx.doi.org/10.1061/(ASCE)0733-9496(1994)120:5(651) - 43. Ljung, L. (1999) System Identification. Theory for the User. Prentice Hall, Upper Saddle River, 609 p.
- 44. Ljung, L. (2007) System Identification toolbox for Use with Matlab. Version 7, 7th Edition, the MathWorks Inc., Natick.
- 45. Moradkhani, H., Sorooshian, S., Gupta, H.V. and Houser, P.R. (2005) Dual State-Parameter Estimation of Hydrological Models Using Ensemble Kalman Filter. Advances in Water Resources, 28, 135-147.
http://dx.doi.org/10.1016/j.advwatres.2004.09.002 - 46. Hsu, K.L., Moradkhani, H. and Sorooshian, S. (2009) A Sequential Bayesian approach for Hydrologic Model Selection and Prediction. Water Resources Research, 45, 1-15.
http://dx.doi.org/10.1029/2008WR006824 - 47. Morales-Velázquez, M.I., Aparicio Mijares, F.J. and Valdés, J.B. (2014) Pronóstico de avenidas utilizando el filtro de Kalman discreto. Tecnología y Ciencias del Agua, 5, 85-110.
- 48. Grewal, M.S. (2011) Kalman Filtering. In: Lovric, M., Ed., International Encyclopedia of Statistical Science, Springer, Berlin, 705-708.
http://dx.doi.org/10.1007/978-3-642-04898-2_321 - 49. Hargreaves, G.H. and Allen, R.G. (2003) History and Evaluation of Hargreaves Evapotranspiration Equation. Journal of Irrigation and Drainage Engineering, 129, 53-63.
http://dx.doi.org/10.1061/(ASCE)0733-9437(2003)129:1(53) - 50. SMN (2014) Sistema de Información Climática Computarizada CLICOM. Servicio Meteorológico Nacional de México, México.
- 51. BANDAS (2014) Banco Nacional de Aguas Superficiales BANDAS.
http://www.conagua.gob.mx/CONAGUA07/Contenido/Documentos/Portada%20BANDAS.htm - 52. Bastola, S. and Misra, V. (2014) Evaluation of Dynamically Downscaled Reanalysis Precipitation Data for Hydrological Application. Hydrological Processes, 28, 1989-2002.
http://dx.doi.org/10.1002/hyp.9734 - 53. Box, G.E., Jenkins, G.M. and Reinsel, G.C. (2013) Time Series Analysis: Forecasting and Control. 4th Edition, John Wiley & Sons, Hoboken, 746 p.
- 54. Kimura, N., Hsu, M.H., Tsai, M.Y., Tsao, M.C., Yu, S.L. and Tai, A. (2014) A River Flash Flood Forecasting Model Coupled with Ensemble Kalman Filter. Journal of Flood Risk Management, 9, 178-192.
http://dx.doi.org/10.1111/jfr3.12128 - 55. González-Leiva, F., Ibánez-Castillo, L.A., Valdés, J.B., Vázquez-Pena, M.A. and Ruiz-García, A. (2015) Pronóstico de caudales con Filtro de Kalman Discreto en el río Turbio. Tecnología y Ciencias del Agua, 6, 5-24.
- 56. Gelb, A. (1974) Applied Optimal Estimation. MIT Press, Boston, 374 p.
- 57. Valdés, J.B., Mejía-Velázquez, J.M. and Rodríguez-Iturbe, I. (1980) Filtros de Kalman en la hidrología: predicción de descargas fluviales para la operación óptima de embalses. Informe Técnico No. 80-2, Universidad Simón Bolívar, Decanato de Estudios de Posgrado, Posgrado en Planificación e Ingeniería de Recursos Hídricos, Caracas.
- 58. Haykin, S. (2004) Kalman Filtering and Neural Networks. Vol. 47, John Wiley & Sons, Hoboken, 304 p.
- 59. Clark, M.P., Slater, A.G., Rupp, D.E., Woods, R.A., Vrugt, J.A., Gupta, H.V., Wagener, T. and Hay, L.E. (2008) Framework for Understanding Structural Errors (FUSE): A Modular Framework to Diagnose Differences between Hydrological Models. Water Resources Research, 44, 1-14.
http://dx.doi.org/10.1029/2007WR006735 - 60. Boyle, D.P., Gupta, H.V. and Sorooshian, S. (2000) Toward Improved Calibration of Hydrological Models: Combining the Strengths of Manual and Automatic Methods. Water Resources Research, 36, 3663-3674.
http://dx.doi.org/10.1029/2000WR900207 - 61. Nash, J. and Sutcliffe, J.V. (1970) River Flow Forecasting through Conceptual Models Part I—A Discussion of Principles. Journal of Hydrology, 10, 282-290.
http://dx.doi.org/10.1016/0022-1694(70)90255-6 - 62. McCuen, R.H., Knight, Z. and Cutter, A.G. (2006) Evaluation of the Nash-Sutcliffe Efficiency Index. Journal of Hydrologic Engineering, 11, 597-602.
http://dx.doi.org/10.1061/(ASCE)1084-0699(2006)11:6(597) - 63. Duan, Q., Sorooshian, S. and Gupta, V. (1992) Effective and Efficient Global Optimization for Conceptual Rainfall- Runoff Models. Water Resources Research, 28, 1015-1031.
http://dx.doi.org/10.1029/91WR02985 - 64. Duan, Q.Y., Gupta, V.K. and Sorooshian, S. (1993) Shuffled Complex Evolution Approach for Effective and Efficient Global Minimization. Journal of Optimization Theory and Applications, 76, 501-521.
http://dx.doi.org/10.1007/BF00939380 - 65. Shin, M.J., Guillaume, J.H., Croke, B.F. and Jakeman, A.J. (2015) A Review of Foundational Methods for Checking the Structural Identifiability of Models: Results for Rainfall-Runoff. Journal of Hydrology, 520, 1-16.
http://dx.doi.org/10.1016/j.jhydrol.2014.11.040 - 66. Wagener, T., Lees, M.J. and Wheater, H.S. (2001) A Toolkit for the Development and Application of Parsimonious Hydrological Models. In: Singh, V.P. and Frevert, D., Eds., Mathematical Models of Large Watershed Hydrology, Vol 1, Water Resources Publications, Highlands Ranch, 87-136.
- 67. Perrin, C., Michel, C. and Andréassian, V. (2003) Improvement of a Parsimonious Model for Streamflow Simulation. Journal of Hydrology, 279, 275-289.
http://dx.doi.org/10.1016/S0022-1694(03)00225-7 - 68. Koutsoyiannis, D. (2015) Generic and Parsimonious Stochastic Modelling for Hydrology and Beyond. Hydrological Sciences Journal, 61, 225-244.
http://dx.doi.org/10.1080/02626667.2015.1016950 - 69. Scheffler, R., Neill, C., Krusche, A.V. and Elsenbeer, H. (2011) Soil Hydraulic Response to Land-Use Change Associated with the Recent Soybean Expansion at the Amazon Agricultural Frontier. Agriculture, Ecosystems & Environment, 144, 281-289.
http://dx.doi.org/10.1016/j.agee.2011.08.016 - 70. Hsu, K.L., Gupta, H.V., Gao, X., Sorooshian, S. and Imam, B. (2002) Self-Organizing Linear Output Map (SOLO): An Artificial Neural Network Suitable for Hydrologic Modeling and Analysis. Water Resources Research, 38, 38-1-38-17.
http://dx.doi.org/10.1029/2001wr000795 - 71. Farahmand, T., Fleming, S.W. and Quilty, E.J. (2007) Detection and Visualization of Storm Hydrograph Changes under Urbanization: An Impulse Response Approach. Journal of Environmental Management, 85, 93-100.
http://dx.doi.org/10.1016/j.jenvman.2006.08.004 - 72. Sveinsson, O.G., Lall, U., Fortin, V., Perrault, L., Gaudet, J., Zebiak, S. and Kushnir, Y. (2008) Forecasting Spring Reservoir Inflows in Churchill Falls Basin in Quebec, Canada. Journal of Hydrologic Engineering, 13, 426-437.
http://dx.doi.org/10.1061/(ASCE)1084-0699(2008)13:6(426) - 73. Seong, C., Her, Y. and Benham, B.L. (2015) Automatic Calibration Tool for Hydrologic Simulation Program- FORTRAN Using a Shuffled Complex Evolution Algorithm. Water, 7, 503-527.
http://dx.doi.org/10.3390/w7020503
NOTES
*Corresponding author.
1The Matlab runs reported for the HyMod model were conducted using a modeling and optimization toolbox created by H. Gupta, Department of Hydrology and Water Resources, The University of Arizona, USA. The Matlab runs reported for the ARX-DKF model were conducted using an ARX-DKF Toolbox created by the authors.











