Open Journal of Modern Hydrology
Vol.04 No.04(2014), Article ID:50443,11 pages
10.4236/ojmh.2014.44013
Development of Upstream Data-Input Models to Estimate Downstream Peak Flow in Two Mediterranean River Basins of Chile
Roberto Pizarro-Tapia1, Rodrigo Valdés-Pineda1,2*, Claudio Olivares3, Patricio A. González1
1University of Talca, Technological Center of Environmental Hydrology (CTHA), Talca, Chile
2University of Arizona, Department of Hydrology and Water Resources, Tucson, USA
3Ministry of Public Works, Water Resources Directorate (DGA), Coyhaique, Chile
Email: rpizarro@utalca.cl, *rvaldes@email.arizona.edu, claudio.olivares@mop.gov.cl
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 August 2014; revised 8 September 2014; accepted 6 October 2014
ABSTRACT
Accurate flood prediction is an important tool for risk management and hydraulic works design on a watershed scale. The objective of this study was to calibrate and validate 24 linear and non-linear regression models, using only upstream data to estimate real-time downstream flooding. Four cri- tical downstream estimation points in the Mataquito and Maule river basins located in central Chile were selected to estimate peak flows using data from one, two, or three upstream stations. More than one thousand paper-based storm hydrographs were manually analyzed for rainfall events that occurred between 1999 and 2006, in order to determine the best models for predicting down- stream peak flow. The Peak Flow Index (IQP) (defined as the quotient between upstream and downstream data) and the Transit Times (TT) between upstream and downstream points were also obtained and analyzed for each river basin. The Coefficients of Determination (R2), the Standard Error of the Estimate (SEE), and the Bland-Altman test (ACBA) were used to calibrate and validate the best selected model at each basin. Despite the high variability observed in peak flow data, the developed models were able to accurately estimate downstream peak flows using only upstream flow data.
Keywords:
Peak Flows, Storm Events, Flood Forecasting, Peak Flow Index, Peak Flow Transit Time, Linear and No-Linear Models

1. Introduction
Floods are among the most powerful forces on the Earth [1] because they have disastrous effects in terms of casualties, economic impacts and infrastructure damages [2] [3] . Severe damages generated by flooding events in the central zone of Chile have destroyed bridges and irrigation canals. To prevent such damages, engineers have designed protective structures like dikes, spillways, and stormwater evacuation canals, whose designs require the estimation of peak flow values [4] . However, due to their sporadic nature, flooding and its consequences are usually forgotten by the population, which often results in inadequate land planning and management. The establishment of human settlements in zones with a high likelihood of flooding is an example of this.
Flood prediction has become an important social and economic component of risk management [5] . Hydrologic modelling can be used to better understand flood processes and thus can more precisely predict flash floods [6] . In this sense, the application of indirect methods for the estimation of peak flows in ungauged watersheds could be assumed mainly in three different ways: 1) The Unit Hydrograph [7] ; 2) The Curve Number Method [8] - [10] ; 3) Empirical Formulas [11] . In Chile different Empirical Formulas like DGA-AC [12] , the Verni- King approach [13] modified by [12] and the Rational Method [11] using tabulated runoff and frequency coefficients defined by [12] , have been traditionally used to estimate peak flows in ungauged basins. Other recent approaches have dealt with the calibration and validation of physically based distributed precipitation-runoff models [14] and also empirical-based methods, such as the quantile regression approach applied by [4] who used flow records of 25 watersheds located in Central Chile (32˚45'S to 43˚50'S) to estimate design peak flows in medium-large watersheds (100 - 5000 km2). Because of the high flood frequency in Central Chile and the lack of studies related to the topic, the objective of this study was to determine if upstream peak-flow data could be used to accurately predict flooding downstream in real-time, by calibrating and validating 24 linear and non-linear regression models in two important rivers located in the Mediterranean zone of Chile between 34˚41'S and 36˚33'S. The validity of the best selected models at each basin is evaluated by comparing its results with the observed peak flows through statistical measures, such as the Coefficient of Determination (R2), the Standard Error of the Estimate (SEE), and the Bland-Altman test (ACBA).
2. Methodology
2.1. Study Area and Dataset
The study was implemented in two rivers located in the first-order administrative region of Maule in central Chile (34˚41'S and 36˚33'S latitudes) (see Figure 1). The local climate is temperate humid (Mediterranean), characterized by dry summers with mean annual precipitation of up to 1336 mm∙yr−1, of which 57% and 43% in terms of volume are contributed to runoff or evaporation respectively [15] . For its part, [16] stated that 80% of the precipitation in central Chile falls in the rainy season from May-August, typically peaking during June. The surface area of Maule is 30469.1 km2, which represents 4% of the national continental territory [17] . The
Figure 1. Study area and numbers in the figure identifying the stream gauging stations listed in Table 1.
Mataquito River is located in the northern part of the region, and drains an area of approximately 6190 km2. The river begins 12 km east of the city of Curicó at the confluence of two tributaries with headwaters in the Andes Mountains: the Teno River and the Lontué River, which drain the northern and southern parts of the basin respectively [18] . The Maule River is located south of the Mataquito River and is the fourth-largest river in the country, with a drainage area at 20,295 km2. Its headwaters are in the Maule Lake at 2200 meters above sea level [19] .
Instantaneous flow data from 13 stream gauging stations distributed up and downstream of both rivers was first used to make quantity and quality control (Figure 1). Each paper-based record contained date and time for each of storm event occurred from 1999 to 2006 (Table 1). The dataset was provided by the Dirección General de Aguas (DGA), the Chilean government organization in charge of water resources management of Chile (for details see [20] ).
2.2. Downstream Estimation Points
In collaboration with DGA, the estimation points were mainly selected because the high recurrence of flooding. According to this criterion, the Mataquito in Licantén station (located near the town of Licantén) was selected for the Mataquito Basin. In fact, during May 2008, a flood of the Mataquito River resulted in the flooding of 70% of the town [21] . On the other hand, the Maule in Forel station was selected for the Maule Basin, where a historical instantaneous flow of 17,212 m3∙sec−1 was recorded in June 28th, 1993. It is also important to add that two additional stations were selected in this basin: Claro in Rauquén and Loncomilla in Las Brisas, both immediately located upstream from the Maule in Forel station. Summarizing, four downstream estimation points were finally chosen, one in the Mataquito Basin and three in the Maule Basin (for details see Figure 1 and Table 2).
Once the estimation points were chosen, hydrographs were constructed from every identified flood event (storm event), and the estimation points were paired with one, two or three upstream stations. Only instantaneous flows data (m3∙sec−1) containing the date and time for the every upstream and downstream station were selected. Finally a total of 1000 flood events between 1999 and 2006 were chosen for further analysis.
2.3. Peak Flow Index (IQP) and Transit Time (TT)
In order to better understand the relationship between the peak flows recorded at the upstream and downstream stations for each basin, the Peak Flow Index (IQP) was created to describe the quotient between peak flow values at the downstream estimation point and the upstream stations. The index can be calculated as:
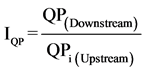
Table 1. Stream gauging stations selected for the study.
Table 2. Downstream estimation points and their upstream stations. The numbers are related to the numbers in the maps.
where,
· IQP is the Peak Flow Index,
· QP(Downstream) is the peak flow recorded downstream,
· QPi(Upstream) is the upstream peak flow recorded at the upstream station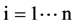 .
.
In the case of analyzing multiple upstream stations, the IQP was established by defining the denominator as the sum of the peak flow values for the “n” upstream stations. As the index is expressed as a quotient, it quantifies how many times the recorded peak flow increased from the upstream station to the downstream estimation point (Figure 2). Additionally, the hydrographs were further analyzed to determine the Transit Time(TT), i.e., the number of hours it takes for a single peak flow event to pass between the upstream station and the downstream estimation points. Transit times (TT) were calculated for all the paired stations in both basins.
2.4. Selection of Linear and No-Linear Regression Models
Both linear and non-linear models were used to determine if downstream peak flows were correlated with those values registered in upstream stations. The mathematical expression to define dependent and independent variables in each regression model was:
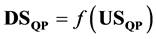
where,
· DSQP is the dependent variable considered as the peak flow for the downstream estimation point,
· USQP is the independent variable considered as the peak flow of the upstream station(s).
Within this context, 24 linear and non-linear mathematical models considering one, two, or three upstream stations were used to estimate peak flows at each estimation point (Table 3).
2.5. Models Calibration
For the model calibration stage, the quantity of data used to adjust every model varied according to the downstream estimation points and upstream stations being considered, due to the differences in the number of flood events for any given station. All storm events of the year were considered and no distinction was made regarding whether flood events occurred in the dry or rainy seasons. The Coefficient of Determination (R2) and the Standard Error of Estimate (SEE) were used to calibrate and validate the models and determine the best mathematical relation to estimate downstream peak flows (Table 4).
where,
· y are the observed values,
· ŷ are the estimated values,
· n is the maximum value in the series,
· t corresponds to each storm-event considered in the analysis, where .
.
Figure 2. IQP for the different paired stations and flood events. IQP quotient is represented in each plot by IQP = [Downstream Station Number/Upstream Station Number], where the numbers are represented in the map and correspond to the paired stations used to calculate the Index. Marker-size represents historical mean maximum instantaneous flow for each selected station (m3∙sec−1). The red dashed line represents the mean values for each paired stations.
Table 3. Dependent and independent variables used for simple and multiple regressions models.
Note: MA is Mataquito in Licantén; MF is Maule en Forel; CR is Claro in Rauquén; LBR is Loncomilla in Las Brisas; ML is Maule in Longitudinal; CC is Claro in Camarico; LR is Lircay in Las Rastras bridge; LBO is Loncomilla in La Bodega; ACH is Achibueno in La Recova; ANC is Ancoa in El Morro; CO is Colorado before Palos; PA is Palos before Colorado; TE is Teno after Claro; QP is Peak flow.
Table 4. Determination Coefficient (R2) and Standard Error of Estimate (SEE).
2.6. Models Validation
Finally, the best three models as determined by the error measurements results (R2 and SEE) were validated by the Bland-Altman test (ACBA), which evaluates the degree to which the data obtained through direct observation differ from the theoretical response obtained from a model, and also determines if these differences are acceptable on a hydro-meteorological basis [22] . In statistical terms, the amount of agreement is measured as the mean differences (DP) between the observed and estimated data and the standard deviation (SD) of these differences. Additionally, the 95% limits of agreement (LC) are also often computed and are defined as:
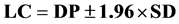
The model in which the observed and the estimated data have DP values closest to zero in absolute terms is considered the more accurate. In the case of an equal or minimal difference between the DP values, then the model with the smallest SD value and the narrowest limits of agreement is determined to be more accurate [23] . The results from the Bland-Altman test were used to verify the best performing models for each of the four downstream estimation points.
3. Results and Discussion
3.1. Streamflows and Rainfall Variability Indexes
The fluctuation of streamflow and precipitation in the Aconcagua basin in Chile were studied by [24] determining that ENSO significantly affects the diverse physical processes controlling the hydrometeorology of the river basin. During El Niño years annual and winter precipitation significantly increase, especially along the coast. [25] , analyzed the possible ENSO influence in Sudamerican Rivers, and have confirmed the presence of a seasonal behavior of the rivers located in Central Chile, with increasing monthly flows associated to El Niño events, and decreasing monthly flows associated to La Niña events. A similar seasonal behavior in the Mataquito basin was found by [26] who observed an increasing difference between average stream flows in the rainy season as compared to the snowmelt season, indicating that part of this trend is caused by larger flows during fall months. [27] studied the spatial and temporal variability of streamflow in south-central Chile (between latitudes 34˚S and 45˚S) and determined that in addition to ENSO, there are two other phenomena that strongly influence summertime streamflow: the Antarctic oscillation (AAO) and the Pacific Decadal Oscillation (PDO). Additionally, the authors found significant decreases in streamflow between latitudes 37.5˚S and 40˚S, which are consistent with the decreases in precipitation observed and also with lower Southern Oscillation Index (SOI) values. Recently, [28] determined linear correlations between annual and seasonal trends flows and indices of ENSO, through the index of sea surface temperature (SST) for the Aconcagua River, finding positive correlation between the maximum mean monthly flows and El Niño events, negative correlation between minimum monthly mean flows and La Niña events, and a positive correlation between the SST index (Sea Surface Temperature) and the mean monthly flows for the 1950-2000 period, confirming a seasonal flows behavior in Central Chile. Based on the mentioned above, and their final use in the analysis, most of the selected flood events occurred during the months of May and September, which corresponds to the rainy winter season in the study area. In some cases the data analyzed included up to four flood events per month.
3.2. Peak Flow Index (IQP) Comparison
The Peak Flow Index (IQP) accurately determined the quotient increase for downstream peak flows in both the Mataquito and Maule Basins. For the downstream estimation point in the Mataquito Basin with one, two, or three upstream stations, the maximum IQP values varied from 3.1 to 17.4; for the estimation point in the Maule River the IQP values varied from 1.3 to 17.6 for one, two, or three upstream stations, which verified that IQP behaves similarly for the two basins (Table 5).
On the other hand, IQP values corresponding to the sum of the peak flows for two or three upstream stations more closely approximated the observed value downstream than those values calculated with one upstream station, i.e. the IQP value was closer to 1 when two upstream stations were considered. Similarly, the IQP values obtained using three upstream stations suggest that the IQP increases are very similar to the increases in the observed data, as IQP values equal to 1 have less variability is observed in the data. Initially was thought that IQP values could be correlated with the peak flow values for the upstream stations or the downstream estimation points. However, the R2 results do not suggest a correlation. For some downstream estimation points, index values both increase and decrease with an increase in peak flows, while for others no definitive trend exists either way. However, in the case of the upstream stations a slight trend exists between the index and peak flow values, as the index values tend to slightly decrease with larger peak flows.
3.3. Transit Times (TT) Comparison
Peak flow Transit Time (TT) analyses that are reliable are imperative for flood prediction and mitigation. Some authors have stated that transit times may be mostly a function of distance between two stream gauging stations; however, other factors exist that might also influence the peak flow TT, e.g. channel morphology and vegetative cover, among others. In this context, [29] studied the effects of pine plantations and native forest on the peak flow behavior of another tributary river in the Maule Region (the Purapel); they determined that vegetative cover had no significant difference initially on peak flow, and that the variation was instead largely due to precipitation. In addition, [30] analyzed the relationship between peak flows and runoff before and after a forest harvest in southern Chile and determined that mean annual runoff increased by up to 110% after harvesting. The authors also pointed out that factors such as precipitation and channel morphology influenced peak flow behavior in addition to vegetative cover. In this investigation, the lowest average transit time observed in the Mataquito River at the Mataquito in Licantén estimation point was about 20 hours. For the Maule River, the lowest average transit time recorded was close to 4 hours observed at the Loncomilla in La Bodega estimation point. Therefore, peak flows TT at Maule River had the shortest average time for flood risk management activities (Table 6).
3.4. Calibration and Validation of the Best Selected Models
In the absence of sufficient observations of flood extent, flooding risk areas are usually identified using numerical hydraulic models. This requires a dynamic approach to represent transient storage effects [31] . In any event, some form of calibration is required to apply these models successfully to a particular river in a given flood event [32] . In this case, the coefficients of Variation (CV) values for the average peak flow at each station were analyzed showing the highest variability (112.5%) at the Claro in Camarico station in Maule Basin. All the remaining stations in both basins revealed CV values over 60%, suggesting significant variability. Then, linear graphic correlations between upstream and downstream peak flows were developed, the results being highly linear in all cases (Figure 3).
On the other hand, higher average peak flows downstream were related to shorter transit times, based on the relationship between average peak flows at the downstream estimation points and average transit time at the Mataquito and Maule rivers. Nevertheless, the linear correlation between peak flow transit time and peak flow values at each estimation point in both rivers, whether high or low, was very weak. Finally, as indicated previously, R2 and SEE were used as fitting measures to select the three best models for each estimation point; R2 values superior to 0.70 were found for the majority of the models. In the subsequent validation phase, the majority of the R2 values obtained indicated that, in general, the calibrated models accurately represented the variation in the data of the downstream estimation points. In only a few cases SEE and ACBA did not agree with the R2 results obtained. Finally, based on SEE and ACBA results, one model was chosen for based on one, two, or three upstream stations (Table 7). It is also important to note that approximately around 70% of the storm events were used for calibration of each selected model. The remaining data (30%) were used to validate the selected models (Figure 4).
Table 5. Minimum, maximum, and average peak flows and Peak Flow Index (IQP) values for paired time series between downstream estimation points and upstream stations.
Table 6. Average, minimum, and maximum transit times (TT) between the upstream stations and their downstream estimation points.
Figure 3. Scatter plots for downstream and upstream stations in the Mataquito (left column) and Maule (right column) Basins.
Table 7. The best models for the four estimation points according to the number of upstream stations as determined by R2, SEE, and ACBA test results.
Note: MA is Mataquito in Licantén; MF is Maule enForel; CR is Claro in Rauquén; LBR is Loncomilla in Las Brisas; ML is Maule in Longitudinal; CC is Claro in Camarico; LR is Lircay in Las Rastras bridge; LBO is Loncomilla in La Bodega; ACH is Achibueno in La Recova; ANC is Ancoa in El Morro; CO is Colorado before Palos; PA is Palos before Colorado; TE is Teno after Claro; QP is Peak flow.
Figure 4. Observed and estimated peak flow values for the Maule in Forel (MFQP) station considering input data from two upstream stations: Colorado in Rauquén (CRQP) and Loncomilla in Las Brisas (LBRQP).
4. Conclusion
The Peak Flow Index (IQP) accurately represented the relationship between upstream and downstream flows. The transit time (TT) was lower in Maule basin, despite its greater extent (which could imply more traveling time for the flooding wave). In general, for both Maule and Mataquito rivers various mathematical models were able to accurately estimate downstream peak flows using upstream data. However, there were points at which the linear models were more accurate than the more complex models using upstream information in the analyzed basins. Finally, it is important to point out that it is possible to use only upstream data to predict peak flows downstream. This is a good and relatively inexpensive approach for modeling flooding in real time, and it is useful when—as is often the case—extensive data needed for more complex models are unavailable. Furthermore, this simple streamflow-data approach can be used by national agencies like DGA to improve flood risk mitigation measures.
Acknowledgements
The authors would like to express their gratitude to the Dirección General de Aguas de Chile (DGA) and a directorate of the Ministry of Public Works for providing the paper-based dataset used in this study.
References
- O’Connor, J.E. and Costa, J. (2004) The World’s Largest Floods, Past and Present: Their Causes and Magnitudes. USA Geological Survey Circular 1254, USA Department of the Interior, Washington DC.
- Morss, R.E., Wilhelmi, O.V., Downton, M.W. and Gruntfest, E. (2005) Flood Risk, Uncertainty, and Scientific Information for Decision Making: Lessons from an Interdisciplinary Project. Bulletin of the American Meteorological Society, 86, 1593-1601. http://dx.doi.org/10.1175/BAMS-86-11-1593
- Carter, N.T. (2009) Federal Flood Policy Challenges: Lessons from the 2008 Midwest Flood. Congressional Research Service, 7-5700, Washington DC. http://www.floods.org/PDF/2008_MidwestFloods/CR_Lessons_Learned_from_the_2008_Midwest_Flood.pdf
- Muñoz, E., Arumí, J.L. and Vargas, J. (2012) A Design Peak Flow Estimation Method for Medium-Large and Data- Scarce Watersheds with Frontal Rainfall. Journal of the American Water Resources Association, 48, 439-448. http://dx.doi.org/10.1111/j.1752-1688.2011.00622.x
- Tucci, C.E.M. and Collischonn, W. (2006) Predicción de crecidas. Boletín de la OMM, 55, 179-184.
- Estupina-Borrell, V., Dartus, D. and Ababou, R. (2006) Flash Flood Modeling with the MARINE Hydrological Distributed Model. Hydrology and Earth System Sciences Discussions, 3, 3397-3438. http://dx.doi.org/10.5194/hessd-3-3397-2006
- Linsley, R., Kohler, M. and Paulhus, J. (1986) Hydrology for Engineers. 3rd Edition, McGraw-Hill Publications, New York.
- Soil Conservation Service (SCS) (1964) National Engineering Handbook, Section 4: Hydrology. Department of Agriculture, Washington DC, 450 p.
- Soil Conservation Service (SCS) (1972) National Engineering Handbook, Section 4: Hydrology. Department of Agriculture, Washington DC, 762 p.
- Titmarsh, G., Cordery, I. and Piligrim, D. (1995) Calibration Procedures for Rational and USSCS Design Flood Methods. Journal of Hydraulic Engineering, 121, 61-70. http://dx.doi.org/10.1061/(ASCE)0733-9429(1995)121:1(61)
- Chow, V.T. (1964) Handbook of Applied Hydrology. McGraw-Hill Publications, New York.
- Dirección General de Aguas (DGA) (1995) Manual de cálculo de crecidas y caudales mínimos en cuencas sin infor- mación fluviométrica. http://documentos.dga.cl/FLU398.pdf
- Verni, F. and King, H. (1977) Estimación de crecidas en cuencas no controladas. III Coloquio, Sociedad Chilena de Ingeniería Hidráulica, Santiago, 357-374.
- Stehr, A., Aguayo, M., Link, O., Parra, O., Romero, F. And Alcayaga, H. (2010) Modeling the Hydrologic Response of a Mesoscale Andean Watershed to Changes in Land Use Patterns for Environmental Planning. Hydrology and Earth System Sciences, 14, 1963-1977. http://dx.doi.org/10.5194/hess-14-1963-2010
- Inzunza, J. (2005) Clasificación de los Climas de Köppen. Revista Ciencia Ahora, 15, 14.
- Falvey, M. and Garreaud, R. (2007) Wintertime Precipitation Episodes in Central Chile: Associated Meteorological Conditions and Orographic Influences. Journal of Hydrometeorology, 8, 171-193. http://dx.doi.org/10.1175/JHM562.1
- Biblioteca del Congreso Nacional de Chile (BCN) (2014) Región del Maule. http://siit2.bcn.cl/nuestropais/region7
- Dirección General de Aguas (DGA) (2004) Diagnóstico y Clasificación de los Cursos y Cuerpos de Agua Según Obje- tivos de Calidad: Cuenca Río Mataquito. http://www.sinia.cl/1292/articles-31018_Mataquito.pdf
- Dirección General de Aguas (DGA) (2004) Diagnóstico y Clasificación de los Cursos y Cuerpos de Agua Según Obje- tivos de Calidad: Cuenca del Río Maule. Ministerio de Obras Públicas, Gobierno de Chile. http://www.sinia.cl/1292/articles-31018_Maule.pdf
- Valdés-Pineda, R., Pizarro, R., García-Chevesich, P., Valdés, J.B., Olivares, C., Vera, M., Balocchi, F., Pérez, F., Vallejos, C., Fuentes, R., Abarza, A. and Helwig, B. (2014) Water Governance in Chile: Availability, Management and Climate Change. Journal of Hydrology, in Press. http://dx.doi.org/10.1016/j.jhydrol.2014.04.016
- Dirección General de Aguas (DGA) (2008) Informe técnico: Análisis crecida río Mataquito y tributarios 22 y 23 de mayo de 2008. Ministerio de Obras Públicas de Chile, Santiago.
- Llamas (1993) Hidrología General. Edición española, Servicio Editorial Universidad del País Vasco, 635 p.
- Bland, J. and Altman, D. (1999) Measuring Agreement in Method Comparison Studies. Statistical Methods in Medical Research, 8, 135-160. http://dx.doi.org/10.1191/096228099673819272
- Waylen, P. and Caviedes, C. (1990) Annual and Seasonal Fluctuations of Precipitations and Stream Flow in the Aconcagua River Basin, Chile. Journal of Hydrology, 120, 79-102. http://dx.doi.org/10.1016/0022-1694(90)90143-L
- Caviedes, C. and Waylen, P. (1998) Respuesta del clima de América del Sur a las fases de ENSO. Bulletin de l’Institut Français d’Études Andines, 27, 613-626.
- Vicuña, S., Gironás, J., Meza, F., Cruzat, M., Jelinek, M. and Poblete, D. (2011) When Hydrologic Extremes Are Not Driven by Climatic Extremes: Exploring a Climate Change Hydrologic Extreme Attribution Example in South Central Chile. Fall Meeting 2011, Abstract#GC51E-1044, American Geophysical Union, Washington DC.
- Rubio-Álvarez, E. and McPhee, J. (2010) Patterns of Spatial and Temporal Variability in Stream Flow Records in South Central Chile in the Period 1952-2003. Water Resources Research, 46, 16. http://dx.doi.org/10.1029/2009WR007982
- Martínez, C., Fernández, A. and Rubio, P. (2012) Caudales y variabilidad climática en una cuenca de latitudes medias en Sudamérica: Río Aconcagua, Chile central (33˚S). Boletín de la Asociación de Geógrafos Españoles, 58, 227-248.
- Pizarro, R., Araya, S., Jordán, C., Farías, C., Flores, J.P. and Bro, P. (2006) The Effects of Changes in Vegetative Cover on River Flows in the Purapel River Basin of Central Chile. Journal of Hydrology, 327, 249-257. http://dx.doi.org/10.1016/j.jhydrol.2005.11.020
- Iruomé, A., Mayen, O. and Huber, A. (2006) Runoff and Peak Flow Responses to Timber Harvest and Forest Age in Southern Chile. Hydrological Processes, 20, 37-50. http://dx.doi.org/10.1002/hyp.5897
- Wheater, H.S. (2002) Progress and Prospects for Fluvial Flood Modeling. Philosophical Transactions of the Royal Society A, 360, 1409-1431. http://dx.doi.org/10.1098/rsta.2002.1007
- Hunter, N., Bates, P., Horrit, M., De Roo, P.J. and Werner, M. (2005) Utility of Different Data Types for Calibrating Flood Inundation Models within a GLUE Framework. Hydrology and Earth System Sciences, 9, 412-430. http://dx.doi.org/10.5194/hess-9-412-2005
NOTES
*Corresponding author.







