Open Journal of Forestry
Vol.04 No.04(2014), Article ID:47744,10 pages
10.4236/ojf.2014.44038
Diameter Measurements of the Upper Parts of Trees Using an Ultra-Telephoto Digital Photography System
Akira Shimizu1*, Shigeki Yamada2, Yuichiro Arita3
1Kyushu Research Centre, Forestry and Forest Products Research Institute, Kumamoto, Japan
2Forestry and Forest Products Research Institute, Tsukuba, Japan
3Ogunimachi Forestry Cooperative, Oguni-Machi, Japan
Email: *akiraxx@ffpri.affrc.go.jp
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 May 2014; revised 10 June 2014; accepted 23 June 2014
ABSTRACT
We develop a new technique to measure the exact upper diameters of trees that is comparatively simple and inexpensive. We can measure the diameters of entire tree trunks efficiently and with high precision. The system uses a digital camera with a ~15 - 30× telephoto lens to take a photograph that can be used for measuring the diameter of the upper part of a comparatively slender tree trunk. Since this method requires a measuring distance and the height of the target point in the image, a range finder capable of measuring angles was combined with the main digiscoping system. A range finder sensor uses a laser and makes a 360 degree angle of observation possible. The diameter of a target position of the objective tree can be obtained by measuring the digital image using image editing software and calculations from spreadsheet software. We focus on the Japanese cedar species in the southwestern part of Japan. Photographic measurements were obtained prior to thinning. The estimates that we obtained largely agree with the true measurements of all trees. With regard to the estimated accuracy of all measured trees, the maximum error ratio was 7.0% (1.45 cm), with a ~2% - 4% error for most of the estimated results. Although the absolute value of the estimation error was 1.87 cm (5.3%) at the maximum (9.87 m in height and 35.5 cm in diameter), an estimation accuracy of <1 cm was reproduced in almost all measurements except for the extreme hypertrophy portion by butt swelling.
Keywords:
Digital Camera, Image Editing Software, Magnifications, Spotting Scope, Taper Curve, Upper Diameter

1. Introduction
Accurate measurements related to stem diameter in the upper canopies of individual trees in a forest are important for understanding forest structure. These data can be used to estimate the three-dimensional distribution of various forest elements (trunks, twigs, leaves) or, more directly, to measure trunk respiration rates (Pruyn et al., 2003); these types of data are also very useful in stem flow analysis and studies of related rain interception phenomena. Furthermore, foresters and silviculturists need to calculate the growing stock of forests; knowledge of timber volume is an important factor in the management of forest plantations (Masutani et al., 1981). High-pre- cision data related to timber volume are most definitely required prior to conducting various forest management techniques.
After the 1970s, dendrometers such as the Barr and Stroud FP15 (Masutani et al., 1981; Williams et al., 1999), Zeiss Telemeter Teletop (Bower, 1971), Breithaupt Todis (Eller & Keister, 1979), and others were used in the Rangefinder dendrometer and Wheeler pentaprism (Parker &Matney, 1999), which used an optical caliper for the direct accurate measurement of upper tree stem diameters. However, the manufacture and sale of most of these instruments was discontinued (Ferguson et al., 1984). Meanwhile, the Criterion laser instrument measuring device, which can easily measure an upper tree stem diameter during felling operations (Williams et al., 1999), is considered to be useful for accurately measuring relatively large trees. A measuring method that uses both an analog and a digital camera also exists. For example, while Takahashi et al. (1997) proposed a diameter and height measurement system using a special camera and Clark et al. (2000b) studied the use of a digital camera system, among others, many significant cost- or accuracy-related improvements can be made; Clark et al. (2000a) provide a summary of this research.
According to the summary of Clark et al., several representative instruments exist. Various types of instru- ments were developed in the Barr and Stroud FP15 represents the last iteration. Although the instrument is thought to be high precision, it is very expensive and is not currently commercially available. On the one hand, although the Criterion is a product that is used today, it is a bit heavy and is mainly suitable for measurements of large trees via the handling process. Furthermore, the research of Takahashi et al. (1997) and Clark et al. (2000b) utilized a camera to make measurements; this work is important in that it is the same approach as this proposed research. Although the method of Takahashi et al. uses a specific film camera that is not a mainstream product and is not employed presently, this technique is similar to our method of determining diameter using a personal computer based on the image photographed with a telephoto lens. Furthermore, although the method of Clark et al. is also similar to our method in its fundamental approach, there is a difference in that the research goals of Clark et al. are diameter, tree height measurement, and timber volume estimation. Therefore, since the magnifi- cation of the camera that is used is comparatively low, the method of Clarke et al. is distinct from our estimation of a highly precise upper diameter.
Both research techniques are based on optical measurements using a camera and these methodologies are ac- cordingly considered to fall into the same groups as the method proposed here. However, the method proposed here yields a large improvement in terms of convenience and accuracy since the technique incorporates both digital equipment (ultra-telephotographic digital camera) and a range finder capable of measuring angles. Hu- man-induced errors caused by different individuals making measurements are minimal because photography is primarily employed; there is very little mechanical control. Furthermore, we propose that this observational sys- tem could satisfy the measurement requirements of high precision at an inexpensive cost because a decline in price is expected for digital camera and ultra-telescopes.
The purpose of this paper is to develop a new technique to measure exact upper diameters of trees in a manner that is both comparatively simple and inexpensive. Such a technique is currently required not only for the pre- sent forestry situation but also for various forest environmental aims. The system developed here enables effici- ent, high-precision measurements of the diameters of entire tree trunks, comparable to dendrometers such as the Barr and Stroud FP15. Here, we introduce the composition of this system, discuss the usage method, highlight the calculation procedure, and summarize the on-site results. The system uses a digital camera with a ~20 - 30× telephoto lens to take a photograph that can be used for measuring the diameter of the upper part of a compara- tively slender tree trunk. This system was developed with the goal of enabling accurate measurements, which are necessary for precise estimates of timber volume in a plantation forest and calculations of the stem surface area for measuring rainfall interception phenomena or stem respiration. Therefore, this paper focuses on the pro- cedure in upper-diameter measurements and taper estimations of individual trees using this method.
The exact log size information gathered from this method constitutes effective resource information, in con- trast to the conventional information of tree diameter and height. If complete count surveys are performed for an entire forest stand, the stand can be used as a certain kind of lumberyard that contains diameter class and log size information. Hence, the system will contribute to forest management plans that utilize forest resources for various purposes, such as structural material, plywood, and biomass utilization. Moreover, since the accuracy of this method is almost equivalent to that of the Barr and Stroud FP15 dendrometer, the system developed here could be used for many investigations requiring this level of accuracy. The tree taper information produced from the upper diameter of an exact individual tree may not only be valuable information for the forest management with regard to forest resources such as effective timber volume and whole trunk timber volume, but could offer in- formation that could also be used for various forest environment assessments. In addition, since the method is comparatively inexpensive and handling is also easy, various on-site applications are expected (e.g., complete enumeration, a sampling survey corresponding to the necessary accuracy).
Furthermore, the proposed measuring method deals with a tree cross section as a right round circle in this study, although both a contact and a non-contact type dendrometer induce error due to the cross-sectional shape of a stem when calculating values of basal area. In other words, the proposed method is the estimation method of the diameter positioned in the front of the photography direction.
2. Material and Methods
2.1. The Measuring System
The measuring system first directly photographs the stem diameter in the upper positions in a forest using a camera with a ~20 - 30× telephoto lens. Next, the diameter of a target position of the objective tree is obtained by measuring the digital image using image editing software such as Adobe Photoshop. Photography in a forest requires more light than normal and a high-magnification camera lens with a focal length >500 mm, which is 10× magnification for the equivalent 35 mm film; such a set-up is very large and expensive. Furthermore, high-magnification photography requires the observer to make these types of measurements using a magnifica- tion of at least 20× or more. Therefore, for high magnification, a very large and expensive special lens with a focal length longer than 1000 mm is needed; a normal camera cannot meet these requirements.
We developed an ultra-telephotographic system that, when combined with a comparatively inexpensive spot- ting scope and digital camera, does not require the use of a special, expensive ultra-telephoto lens. This techni- que allowed us to keep costs low and maintain the advantage of easy use, since the digital camera lens is not as large as a camera with a telescopic lens. We selected a spotting scope with a 15 - 30× magnification that was modified by changing the eyepiece. We used a digital camera that did not cause mechanical vignetting on a screen when used with a spotting scope and adapters. This simple photographic technique, which is called di- giscoping, consists of a camera, a spotting scope, and some corresponding adapters with a stable tripod.
Measuring the distance and height of target points in the imaging is necessary for calculations in this method; in addition to the main digiscoping system, a range finder capable of measuring angles was combined with the equipment. A range finder sensor uses a laser and makes it possible to observe a full 360 degrees. The range of a measurement angle is typically ~45 degrees (an ascending and descending vertical angle) in general measuring, although the angle varied more for taller standing target trees or in some positions used for photography. Also, since shots in the ascending vertical angle of ≥45 degrees were needed for very tall trees and the clear length was not less than 20 m, the system used a range finder that can measure up to 360 degrees. The range finder was adjusted and fixed so the laser pointer from the range finder could be displayed on the center of the photograph in the horizontal position in combination with the laser range finder in the digiscoping system discussed above. This photographic system, which consists of a digiscoping system and a 360 degree range finder, is called a dig- ital-scope photography system (DSPS). Such a system is able to acquire a distance between a tree and the cam- era; the height of a measured point can also be obtained.
The equipment that is necessary for measurements includes a digital camera, a spotting scope with a 15 - 30× magnification, adapters with a stable tripod, and a range finder with mount and splicing fittings capable of mea- suring angles. The total costs of equipment are under ~2000 - 2500 USD. Photographs are processed using im- age processing software (for example, Adobe software or any free software) and calculations of an upper di- ameter are performed with basic spreadsheets (for example, Microsoft Excel or any free software). Therefore, if any freeware is used, additional costs will not be incurred. As a result, the system is comparatively less expen- sive than other measurement systems.
2.2. Photography Procedure
Figure 1 shows the DSPS. A spotting scope and digital camera, connection adapters, a laser range finder with angle measurement, a camera platform, and a stable tripod (with a spirit level) are set up at the point where pho- tographs will be taken and the measurements are then carried out. Based on the measurement target, selecting a location where one can photograph about 3 - 5 standing trees was considered necessary to increase efficiency. Upper diameter pictures were taken at ~4 m intervals among the 1.2 - 21.0 m heights corresponding to the height of the tree being studied. The photographic exposure was automatic, in ±0.3 steps. Three pictures were taken at each diameter measuring point, and a range finder and measuring stick were used for efficiency comparison of height observations. The photography can be done quickly with a measuring stick, but a second person is needed to assist with visual confirmation. Also, one advantage of using a range finder with angle measurements for photography is that it can be operated by one person. However, having two people present is more generally more efficient.
In actual photography, the focal point is focused on an object and the red mark of a laser pointer is checked to confirm the photograph’s range. A remote release is used to prevent shaking the camera. Photography is performed in a way that makes the target object, the diameter of a standing tree, take up more than 1/3 of the entire photograph. Also, distortion by the position on a photograph is not taken into consideration, because the DSPS performs diameter calculations on the basis of an ultra-telephotographic picture. At the same time, the distance and the angle of inclination to the object point are recorded using a range finder with an angle measurement function.
2.3. The Calculation Method of Upper-Level Trunk Diameters Using Digital Image Picture Measurements
First, prior to collecting data for this study, preliminary photography was performed to obtain the criterion data for calculations at ~10 m intervals using a target ruler in an open flat place with a clear ~30 m field of view to set up the camera. This methodology is required to carry out the scale compensation of the synthetic photography characteristics of the optical apparatus, such as the combination of a telescopic lens, a digital camera, and connection adapters. Fundamentally, although a general conversion ratio is determined from the specifications of the camera and spotting scope, it is desirable to create a unified scale compensation regression from directly measured data. This unified scale compensation makes it possible to obtain an exact diameter estimate because several adapters and some fine tuning are required to use this system. A steel ruler exactly 30 cm long was photographed at the track so the horizontal distance could be accurately measured to obtain the relationship between distance and scale compensation. We took photographs of the steel ruler at ~10 m intervals (10, 20, and 30 m). The linear regression between the conversion length per pixel on the image and object distance was created using these ruler images. Using the created conversion equation, we were able to convert pixels to an actual length,
Figure 1. Digital-scope photography system (DSPS).
corresponding to the distance to the target tree point. Equation (1) is the regression equation:
 (1)
(1)
where y is the length (mm) per pixel and x is the object distance (m) (from the camera to the target). This equa- tion is also a relation between distance and a scale.
Although there is essentially no fundamental difference between the method of determining the system’s focal length discussed later and this conversion method, calculating the scale compensation of picture data using dis- tance is facilitated by creating a linear regression between the image value and distance without any detailed knowledge related to the photograph (such as focal length, for example).
Next, the target diameter was computed from upper trunk diameter photograph data using regression analysis. The detailed procedure is as follows:
1) Using image editing software, such as a Photoshop, open the target photographs and measure the diameter (horizontal length) in pixel units.
2) The actual upper diameter is determined by calculating in mm units from the acquired pixel value using the created regression. First, the length (mm) per pixel on a photograph is determined from the distance to target point using Equation (1). Next, an actual diameter value (mm) is obtained by multiplying the diameter in pixel units by this length value.
Images will typically be downloaded and diameters computed in a laboratory after the photography is com- plete for all target trees in the field. However, the operations can be carried out by loading image data after the photography is complete using a notebook computer in the field, in special cases where the upper diameter data is immediately required on-site. Since this calculation is based on a simple linear equation, if regression para- meters need to be input beforehand for spreadsheet software, such as Excel, the actual upper trunk diameters can be computed by simply inputting the pixel value of the recorded diameter using image editing software. In this case, although the photographs are not taken using a horizontal angle of zero, compensation for the vertical an- gle of a digital image was not performed because the target diameter occupied a significant fraction (≥1/3) of the horizontal range in the central part of the image using the ultra-telephotographic system.
In practical photography, a 30× eyepiece was attached to the spotting scope; the magnification of the compact digital camera was set to the standard position (36 mm by standard lens conversion). Therefore, most of the photography was performed using a fixed magnification. If the target diameter size did not take up more than 1/3 of the photograph, the optical zoom of the digital camera was used to increase the magnification so the target diameter covered more than 1/3 of the width of the image. In these digital images, additional adjustment by magnification conversion was performed after the usual operations. The adjustment of the magnification was done using the ratio of the whole number of pixels between the standard and zoomed-in digital images. There- fore, even if a particular tree was very tall and also had a small upper diameter, photography and calculation were still possible without any problems.
Although regression and data conversion were performed in calculating this estimate, a comparable level of accuracy could be attained using a focal length of a system calculated using the data from prepared photography. In this case, the calculation was performed using Equation (2):
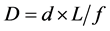 (2)
(2)
where D is the actual length (the object space dimension), d is the image measurement, f is the focal length of the camera, and L is the distance between the lens and the object. Since the calculation of focal length was complicated and the meaning of the system’s focal length is slightly unclear, an estimation using regression was selected in this method. The average focal length of the system was calculated to be 1128.72 mm using Equation (2).
Here, the system measurement accuracy is comprehensively considered. Since the principle of this method is based on an optical system, the measurement accuracy does not change substantially with target tree size in the case of a 100 cm diameter at breast height (DBH) large tree or a 10 cm DBH small tree. However, since the object size per pixel in a photograph changes according to object distance, an error may be expanded according to photographic conditions. If a relatively large standing tree is targeted, it is expected that the object distance is not less than 30 m. In this case, since object size per pixel becomes larger than for a shorter distance, the influence is checked using Equation (1) and the photograph data taken at 10 - 30 m distances in unobstructed, flat places. The measurement error is less than 3% at the maximum for the 30 m measurement distance and there was no increase in the error with increasing distance. In addition, the error was within 3% of the error calculated with the system focal length was determined using Equation (2). Consequently, if the photography was properly performed under the right conditions, one can presume that the diameter estimation was likely within the 3% error range. Since the focal length of the system corresponded to an ultra-telephoto set up, it is likely that there is little to no influence from object distance or photography angle, owing to the lack of distortion in the general measurement range (<~50 m). We again recommend that the target diameter occupies 1/3 or more of the photograph in the horizontal direction.
3. Results and Discussion
3.1. Research Site and Method
The study area’s forest stands are in southwestern Japan and are managed by the Ogunimachi Forestry Cooperative in Kumamoto Prefecture (Figure 2). Thinning is planned in the forest stands of the study area at the owner’s request and the species is Japanese cedar (Cryptomeria japonica). Photographic measurements were taken prior to thinning. After thinning, the logs were cut into ~3 - 4 m lengths. The bottom end diameter, including root swelling around the base of the stem, and length of each log was measured on-site using a steel diameter tape. Table 1 lists the specifications of the three forest stands. The upper diameters were calculated for 5 - 6 target trees that were selected for thinning in each forest studied using this system. Also, photographs were taken using 12 m and 20 m measuring sticks placed beside a tree to field check the height measurements and the accuracy of the range finder.
Three plots were included in this study. Plot 1, with larger trees than those in Plot 2, had trees with an average DBH of 32.7 cm, an average tree height of 26.1 m, and a forest age of 38 years; the plot itself had 1049 stems/ha. When 3 - 4 m bucking was performed, a height of ~20 m was used. The maximum measuring height was near 16 - 20 m for this photographic technique.
Plot 2 had shorter trees and a higher stand density than Plot 1 (Table 1). Therefore, photographic measurements were carried out primarily at a height of 12 - 16 m. Plot 3 is an older stand with taller trees and a high clear length. The range of photographic measurements is possible up to ~22 m. Figure 3 shows the upper diameter for measurements of target tree 5 in Plot 3. Since each plot differed in the slope azimuth (Table 1), photographs were taken at all times except when the sun was shining directly toward the camera. While each digital image was bright, this brightness did not create measurement problems. However, some problems such as shaking or blurring depending on the surrounding conditions might occur. Therefore, three photographs were captured at each photo point using different exposure times.
We have acquired data of standing trees with different clear lengths ranging from 12 - 21 m. Furthermore, 12 and 20 m measurement sticks were used to simplify target height observation and to check the position of the laser pointer. The accuracy of the laser pointer was thereby confirmed and information about using measurement sticks was acquired for height measuring efficiency. That is, when the shorter trees (<~16 m clear length) were
Figure 2. Location of the research site.
Table 1. Summary of observation plots (Japanese cedar).
measured in Plot 2, use of the 12 m measurement stick decreased the time necessary for photography since this methodology eliminated the time needed to use the laser pointer. Based on local geographical features, research could be conducted more efficiently in comparatively flat areas with shorter trees with the second person hold- ing a measurement stick. When the trees were >~20 m clear length, handling the 20 m measurement stick be- came extremely difficult and was too time consuming.
The measurements were conducted in three plots land that included both sloped area and flatland, as described above. The operating efficiencies are compared using the measurement results from the actual forest area. Al- though the size of an object tree became a major factor impacting operating efficiency, as discussed above (the maximum tree height is ~30 m), the operating proceeded rapidly in flatland since the work was easy in that en- vironment. In the flatland forest, we typically required fewer than ~2 hours to measure 5 target trees (from the installation of the measurement system to completion). On the other hand, it took ~3 hours to study the same number of stems in the sloped site. Because the upper diameter was measured every 4 m for each object tree, five or more points on average were selected in total for each tree. Although the measuring data were obtained at 4 m intervals in the research, the necessary operating time could be decreased if the number of measuring points was reduced, i.e., by increasing the measurement interval corresponding to the measurement purpose. Further- more, since a measurement assistant with a measurement stick was employed to check the measurement position of the laser pointer from the range finder, it is likely that our technique required significantly more time than necessary. We expect that it will be possible to decrease the operating time as our familiarity with the measure- ments increases.
3.2. Comparison of DSPS Estimates and Actual Measurements of Upper Diameters
Because these plots underwent ordinary forest management and thinning operations, the trees were cut into small pieces for sale after felling. As a result, it was difficult to directly measure the upper diameter of the pho- tographic measurement position. The actual diameter corresponding to the position of photographic measure- ment was indirectly surveyed as follows: first, the stump height, the bottom end diameter (mm) of each log, and the log length (cm) was measured sequentially using a steel diameter tape and steel tape. Also, since trees were cut higher than the root swelling and they were also cut into small pieces, it was not possible to directly measure the diameter in the corresponding position in the photograph. Therefore, the estimated diameter corresponding to the actual survey diameter obtained in this way was calculated using linear interpolation with the photograph- ic measurement values and connected with the actual survey position.
Since the purpose of the photographic measurements was to record the upper diameters over a range of 2 m in height to the clear length of the target tree, photographic measurements were made at ~4 m intervals above the DBH position (1.2 m). Consequently, the interval of linear interpolation for computing the upper diameter esti- mate corresponding to actual measurement positions was less than 4 m (Figure 4). Figure 4 shows the estima- tions and observations for target trees No. 2, 4, and 3 in Plots 1, 2, and 3, respectively. The actual measurements of all trees confirmed the estimation based on linear interpolation. The tendency for the diameters to become smaller with increasing height at a relatively uniform rate is confirmed in each ~4 m section of log, except at two points of short interval measurements for a ~2 m size log in Plot 2.
The maximum error ratio of all 16 measured trees was 7.0% (1.45 cm), with a ~2% - 4% error for most of the estimated results. Although the absolute value of the estimation error was 1.87 cm (5.3%) at the maximum (9.87 m in height and 35.5 cm in diameter), an estimation accuracy of less than 1 cm was recovered in almost all measurements, except for the extreme hypertrophy portion by butt swelling. All the errors in the tree lower part were due to the influence of butt swelling. On the other hand, we propose that the large errors (~5% - 7%) at the tree upper part were primarily caused by the error of the range finding at the trunk measurement inside a tree crown. Since there are various objects such as leaves and twigs that interfere with the range finder measurements inside
Figure 3. Measuring stem photographs of No. 5 in Plot 3 (white dots indicate red dots of laser pointer).

Figure 4. Diameter estimation results using DSPS. (a) Results in Plot 1-2; (b) Results in Plot 2-4; (c) Results in Plot 3-3.
a tree crown, we consider that errors might occur in measuring the distance used in calculating the height posi- tion. The differences were within ~3% of the preliminary photography in almost all cases beneath the tree crown base, other than these results. Consequently, in cases where the target position was under the clear length, we propose that the diameter estimation was possible within 3% of the tolerance, independent of the vertical photo- graphic angle. On the other hand, it may be important for maintaining accuracy to pay sufficient attention to the range finding for cases of upper diameter measurements inside a tree crown, not including the influence of root swelling. Most of our estimates were underestimates and ≤20% of our estimates were overestimates.
We measured the taper from near the ground to the tip of the tree using spline interpolation, even though such measurements were beyond the range of the actual measurements. Our data were based on our upper diameter calculation data. First, using the actual diameter values (Figure 5(a)), actual measurement diameter values near the bottom, and the measured tree height, we calculated polynomial expression approximations (using Excel software, for example). Since the polynomial equation could be used to solve for the diameter at an arbitrary height, diameters at a height of 1.2 m and higher positions (4, 8, 12, and 16 m) could be computed. The radii were calculated by dividing the obtained diameters by 2 and the taper interpolation equation was obtained with a spline function. Also, in cases where the polynomial expression approximation was employed, we recovered nearly the same results. However, the spline function was selected as the taper equation this time because some gap may have occurred in tree height in that case. The results are illustrated in Figure 5(b), which shows the relationship between the actual measured points and the estimated taper. For example, for tree No. 4 in Plot 1, which agrees comparatively well from the upper part to the base, the calculation yields an underestimate around


Figure 5. Tree taper using spline interpolation with estimated diameters. (a) Estimated diameter values used for polynomial expression approximation; (b) Taper using spline interpolation of trees in Plot 1-4.
the ground because of the large root swelling (Figure 5(b)). Although direct measurements were possible at ground level and the necessity of DSPS is decreased, the number of measurement points near the ground should be increased in cases where these data will be used for calculating parameters such as biomass. Generally, the data provided a good fit for the taper curve calculation, except for the case where the standing tree had a large root swelling. The taper equation using radius is a useful tool that can easily yield timber volume and surface area of trees using operations such as integration. The spline function of taper was calculated using Mathematica software (Wolfram Research, Champaign, Illinois, USA).
As a result, we obtained precise measurements of upper diameters at a comparatively inexpensive costusing this method. Furthermore, this methodology is simple and easily available, as long as the procedures necessary for execution can be acquired.
3.3. Utilization of DSPS Estimation
Several practical uses of this DSPS measurement method should be expected because it can provide sufficient precision for measurements of the upper diameters of the crowns of standing trees.
First, estimating upper diameters using the DSPS method can provide useful data in the development of a harvest plan; trees can be selected for felling based on log size and intended use.
Second, the form of a standing tree is expressed using a taper curve by calculating a spline function or polynomial expression approximations. The taper curve is primarily divided into a type that uses spline interpolation to interpolate the estimate points by DSPS measurement and a type that uses polynomial approximation; both cases can create the taper polynomial expression simply using appropriate software.
Third, computation of available timber volume or usable tree trunk biomass is possible by integrating the polynomial function; stem surface area can also be calculated. The estimation of usable timber volume provides important information related to local timber stand conditions prior to harvest and contributes to an understanding of the future available timber volume. Furthermore, such an estimation provides useful information related to future and expected increases in forest biomass. This information forms the basis for investigations by forest technicians. Such data are also extremely useful to forest owners for forestry management.
Last, the bole volume and surface area of a standing tree are important elements of stem respiration, rain interception, and transpiration calculations using sap flow observations. In this research, an accurate estimate of stem surface area is needed to calculate stem respiration and raindrop adhesion areas in rainfall interception evaporation; the cross-sectional area information of the upper tree position is an extremely useful element for calculations of transpiration by the sap flow method. Although these data are generally obtained by cutting down a standing tree, the information can be similarly acquired without felling trees by using the taper curve expression of a standing tree. Here, because of limited space constraints, we do not discuss detailed calculations of the taper curve expression (possible with software such as Excel or Mathematica). Additional practical use in field- based forestry, such as effective timber volumes, surface area of bole, and estimations of camber that are directly related to lumber use, are also be expected to be possible.
Although innovative technologies such as Lidar and ground Lidar are being developed today, our aims here are distinct from these methodologies. The purpose of our technique is to measure the upper diameter of an individual tree in a quick, precise, and inexpensive way. This method might yield an accuracy equivalent to the best previous results of individual trees with the Barr and Stroud FP15. Our method is extremely inexpensive compared with methods such as ground Lidar. Consequently, this method has advantages in terms of accuracy and cost for making measurements of the upper diameters of individual trees.
4. Conclusion
We have proposed a new and simple upper diameter measuring method using an ultra-telephotographic system. We have explained the equipment necessary for the photography, the photography and measurement procedure, the required cost, and the measurement operating efficiency. In this system, the photography part consists of ultra-telephotography via a digiscoping system that is composed of a digital camera, a spotting scope and some corresponding adapters with a stable tripod. In addition, the system includes a range finder with an angle measurement function. Image processing and spread sheet softwares are necessary for diameter calculations. If free- ware is used, additional costs can be avoided. Also, since equipment is trending toward lower costs, our methodology is comparatively inexpensive compared with other measurement systems.
As a result of actual measurement sat forest sites, we confirmed that measurements of an upper diameter could be simply performed on the spot using linear regression (between the conversion length per pixel on a pic- ture and object distance) created by preliminary measurements in unobstructed and flat locales. The measurements had an accuracy (~3% of the error) largely consistent with preliminary measurements in clear and flat land, although the precision varied according to parameters such as the target tree shape (e.g., root swelling), stand-structure, topographical conditions. Since the measurement principle of this method is essentially based on an optical system, we presumed that the error was, in most cases, caused by photography conditions. Furthermore, the measuring distance to the target point directly affected the calculation of the diameter. In the case that the maximum error of measurement was caused in the forest site, the decline in precision for the photography and range finding to the objective point were inferred to be the main reasons for the errors; obstructions such as leaves and twigs or branches were thought to be responsible for the inconsistencies. Additionally, we found that a difference occurred in the measurement operating efficiency between flatland forest and forest on a slope because of the installation of the measurement system and prospect conditions. However, we maintain that these problems can be improved as our familiarity with the operations increases.
Finally, with regard to the utilization of the measurement system, we expect that an average taper equation can be created. Such an equation will be useful for harvest investigations or accurately effective timber volume estimates. We also expect that our methodology will prove to be applicable to investigations of biomass resourc- es and detailed stem respiration and rainfall interception research.
Acknowledgements
We express our profound gratitude to forest owner Mr. Yasuyuki Watanabe for allowing us to take measure- ments on his land.
References
- Bower, D. R. (1971). Accuracy of Zeiss Telemeter Teletop and Barr and Stroud Dendrometers. USDA ForServ Res Note, SO-134, 3.
- Clark, N. A., Wynne, R. H., & Schmoldt, D. L. (2000a). A Review of Past Research on Dendrometers. Forest Science, 46, 570-576.
- Clark, N. A., Wynne, R. H., Schmoldt, D. L., & Winn, M. (2000b). An Assessment of the Utility of a Non-Metric Digital Camera for Measuring Standing Trees. Computers and Electronics in Agriculture, 28, 151-169. http://dx.doi.org/10.1016/S0168-1699(00)00125-3
- Eller, R. C., & Keister, T. D. (1979). The Breithaupt Todis Dendrometer. Southern Journal of Applied Forestry, 3, 29-32.
- Ferguson, I. S., O’hara, A. J., Wood, G. B., & Miles, J. A. (1984). Calibrating Dendrometers for Estimating Tree Volumes. Australian Forest Research, 14, 253-263.
- Masutani, T. et al. (1981). Direct Measurement of Merchantable Volume in a Stand-Dendrometry and Taper Equations. Pro- ceedings XVII IUFRO World Congress, 201-206.
- Parker, R. C., & Matney, T. G. (1999). Comparison of Optical Dendrometers for Prediction of Standing Tree Volume. Sou- thern Journal of Applied Forestry, 23, 100-107.
- Pruyn, M. L., Harmon, M. E., & Gartner, B. L. (2003). Stem Respiratory Potential in Six Softwood and Four Hardwood Tree Species in the Central Cascades of Oregon. Oecologia, 137, 10-21. http://dx.doi.org/10.1007/s00442-003-1316-2
- Takahashi, M., Saito, K., Shiraishi, N., Iehara, T., & Takahashi, F. (1997). A Photo Based Measurement System Using a Measuring Camera. Journal of Forest Planning, 3, 1-9.
- Williams, M. S., Cormier, K. L., Briggs, R. G., & Martinez, D. L. (1999). Evaluation of the Barr & Stroud FP15 and Crite- rion 400 Laser Dendrometers for Measuring Upper Stem Diameters and Heights. Forest Science, 45, 53-61.
NOTES

*Corresponding author.






