Open Journal of Acoustics
Vol.4 No.1(2014), Article ID:44035,12 pages DOI:10.4236/oja.2014.41004
Caustic Structure of the Under Water Sound Channel
Vsevolod Petrovich Ivanov, Galina Kalenikovna Ivanova
Institute of Applied Physics, Russian Academy of Sciences, Nizhny Novgorod, Russia
Email: ivg@hydro.appl.sci-nnov.ru
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 6 February 2014; revised 6 March 2014; accepted 13 March 2014
ABSTRACT
Using the ray method, an investigation has been carried out on the structure of caustics in the waveguide assuming the canonical distribution of the sound velocity with depth. Monochromatic point source of sound was on the axis of the waveguide. There is considered water rays only. It is shown that the spatial part of the phase of a running sound wave does not contain the wave propagation direction and is always a positive quantity. When the trajectories are calculated, it is assumed that inversion of rays occurs at an angle of total internal reflection where the reflection coefficient is equal to unity. This eliminates the horizontal part of the trajectories. At other points, the reflection coefficient is assumed to be zero, and the passing coefficient is equal to unity. With this change in the calculation of ray’s trajectories, the basic structure of the caustics remained the same. It is shown that the boundary line of the caustic is a number of foci in which rays intersect with similar angles out of the source and have neighbour times of propagation. Structure of the sound field along the boundary line of the caustic is periodic. Its period coincides with the wavelength of the field radiated by the source.
Keywords:Rays; Running Wave; Sound Field; Caustics; Waveguide

1. Introduction
- We assume that the area of the caustic is that part of the waveguide’s space, in which through each point passes (intersect) two or more rays leaving the source at different but close angles and their phases in the spatial or temporal representation are close or coincide. In caustics field, amplitude is much higher than the average amplitude in other parts of the waveguide. Caustics are generated in waveguides, where the speed of sound has a minimum at a certain depth (axis) and is asymmetric parabola. Existence of a minimum speed of sound is observed in many parts of the world ocean. In such wave-guide rays are the periodic functions of coordinates. Its length is equal to the distance between two points of turn up or down the axis of wave-guide. The length of one period is named a cycle. The cycle depends from an angle of exit the ray from the source. Caustics occuring after rays pass one full cycle from the source. Their number increases as the increase of the number of passing cycles. Fundamental research of caustics and theirs formation and calculation of theirs sound field is consider in monographs . Determination of coordinates of the centers of caustics (CC) does not cause any trouble and is found by calculating the vertical coordinates of all water rays at a fixed horizontal distance. If in one point crossed rays have equal faces then they form a caustic. Vertical coordinates of the rays as a function of the propagation time of rays form curves that have the break point in the CC. If the vertical coordinates of rays represent as a function of the exit angles of rays from the source, each exit point of curve takes form of smooth extremum. A presentation vertical coordinates as a function of ray exit angles from the source at a fixed horizontal distance is given in References - and partially in .
- In monographs, introduce the space model of the caustic and field’s calculation in the space of caustics. It is assumed that a group of adjacent rays can be combined into a beam (ray tube), the cross sectional area of which varies during the propagation. There is introduced focusing factor dependent on the cross-sectional area of the tube and increases with a decrease its cross section. Such a model for calculation of the field in the vicinity CC applies in particular within the some limit of area of the section of tube. So, at the intersection of rays forming the tube, at one point, its cross section tends to zero, and the focusing factor becomes infinite. Therefore in , there is concluded that the ray method of sound field calculation is non-applicable near the CC.
- At ray method the field of each ray is calculated independently from others. According to the principle of supreposition, it is easy to summarize fields of all rays that cross at one point. Even if all water rays pass across one point, then the sum of their fields will be finite value.
- In - , it is made the field calculation in caustics with ray method and account the principle of superposition of ray’s fields. Caustics arise at various distances from the source, above and below the axis of the waveguide. Also it is calculated the spatial structure of the sound field in the area of caustics as a two-dimensional function of the coordinates: the distance from the source and depth of caustic. At present time, the results of - are needed in recalculating. According to - ray tracing must calculate when turning angle is the angle of full internal reflection, but not a horizontal one as in - . This angle depends from the exit angle of the ray from the source. In all previous papers, turning angle of all rays is horizontal regardless of the exit angle.
- The aim of this work is to: 1) additional analysis mentioned in - mistakes in writing the spatial phase of the sound wave and the influence of these errors on the calculation of the sound field in liquid media, and 2) calculation of caustics at the same distances from the source as in , but taking into account the reflection coefficient, considering that it is equal to unity at an angle of full internal reflection, and zero at all other angles along the path, and 3) comparison new calculating with those in .
2. Main Characteristics of Running Acoustic Waves
Let us consider the physical content of the concept of running sound waves. Sound wave, as well as fluctuations in pressure and particle velocity of the liquid caused by the sound source, usually described by a running wave, that satisfy the equations of fluid motion, [13] :
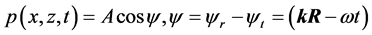 . (1)
. (1)
here the plane wave incidence is the plane with coordinates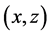 , ω―cycle frequency, t―the time. It is assumed that there is no absorption in the medium. So the amplitude A in (1) is constant. The phase ψ of running wave has two components―the spatial part ψr = kR and the temporary ψt = ωt. Spatial part of the phase kR is the scalar product (SP) of the vectors R (the distance from the source) and k―wave vector parallel to the vector R. To combine scalar value ψt = ωt and vector representation phase ψr, vector k has been introduced, parallel to the vector R. Their SP is equal to the product of modules of vectors kR and does not depend on the choice of coordinate system [14] .
, ω―cycle frequency, t―the time. It is assumed that there is no absorption in the medium. So the amplitude A in (1) is constant. The phase ψ of running wave has two components―the spatial part ψr = kR and the temporary ψt = ωt. Spatial part of the phase kR is the scalar product (SP) of the vectors R (the distance from the source) and k―wave vector parallel to the vector R. To combine scalar value ψt = ωt and vector representation phase ψr, vector k has been introduced, parallel to the vector R. Their SP is equal to the product of modules of vectors kR and does not depend on the choice of coordinate system [14] .
Consider both phase components of the running sound wave. At a given time t, expression (1) defines a function 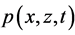 along the vector R as a function of distance. In fact, it is the ray method of calculation of the field. The second part of the phase ψt = ωt reflects the time dependence of the sound wave at a fixed point R. The modulus of vector k is
along the vector R as a function of distance. In fact, it is the ray method of calculation of the field. The second part of the phase ψt = ωt reflects the time dependence of the sound wave at a fixed point R. The modulus of vector k is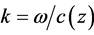 , where
, where 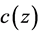 is a sound speed in liquids (ocean) and may be a function of the ocean depth z. Since
is a sound speed in liquids (ocean) and may be a function of the ocean depth z. Since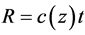 , then kR = ωt. Equality of both parts of the phase ψ, ψr and ψt, means that at any their values the phase of the running wave ψ is equal to zero or the initial phase of the source. In other words, the phase of the running wave is invariant during its propagation, provided that the propagation time and distance is connected with speed of sound
, then kR = ωt. Equality of both parts of the phase ψ, ψr and ψt, means that at any their values the phase of the running wave ψ is equal to zero or the initial phase of the source. In other words, the phase of the running wave is invariant during its propagation, provided that the propagation time and distance is connected with speed of sound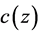 . Phase equality of temporal and spatial description of the oscillatory process reflects the fact that both processes, the oscillating change in time and the wave propagation in space occur simultaneously. In each point come the new values of the emitted signal of the source and the previous values shift to new points in space, forming a running wave.
. Phase equality of temporal and spatial description of the oscillatory process reflects the fact that both processes, the oscillating change in time and the wave propagation in space occur simultaneously. In each point come the new values of the emitted signal of the source and the previous values shift to new points in space, forming a running wave.
Consider the typical mistakes in writing (and understanding) of the spatial phase of the running wave, which is occur in many papers on wave propagation in homogeneous and inhomogeneous media, see, e.g, [1] [2] [13] [15] [16] .
It is believed that the spatial part of the phase ψr contains sign (direction) of the wave propagation. We show that it is misconception in details. Module (length) of vector R is equal: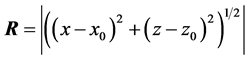 . Here x0, z0 are the initial coordinates, x, z―current coordinates (at moment t) of the vector R. It is seen that the length of R does not depend on the sign of the differences of start and end of coordinates R along the axes, i.e., on the direction of R. The module of vector k is
. Here x0, z0 are the initial coordinates, x, z―current coordinates (at moment t) of the vector R. It is seen that the length of R does not depend on the sign of the differences of start and end of coordinates R along the axes, i.e., on the direction of R. The module of vector k is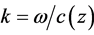 . SP of parallel vectors k, R does not contain their direction too. Indeed, according to [14] , the projections on axes parallel vectors always have the same signs regardless of their orientation relative to the selected coordinate system. SP of
. SP of parallel vectors k, R does not contain their direction too. Indeed, according to [14] , the projections on axes parallel vectors always have the same signs regardless of their orientation relative to the selected coordinate system. SP of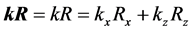 . Here Rx, Rz are projections of vector R at axes x, z. Rx may be written in two forms: Rx = x − x0 or Rx = Rsinθ, θ is the angle between R and positive direction axis z. If x − x0 < 0 (negative) then Rx < 0 and sinθ < 0, kx = ksinθ < 0 and kxRx > 0, so kzRz > 0 too.
. Here Rx, Rz are projections of vector R at axes x, z. Rx may be written in two forms: Rx = x − x0 or Rx = Rsinθ, θ is the angle between R and positive direction axis z. If x − x0 < 0 (negative) then Rx < 0 and sinθ < 0, kx = ksinθ < 0 and kxRx > 0, so kzRz > 0 too.
It follows that the phases ψr of incident and reflected waves from the boundary of the medium do not differ from each other, consist of the sum of positive productions kxRx and kzRz and increases as the wave propagates. This property of the SP of parallel vectors shows that the direction of the sound wave propagation in ψr is absent. For any direction of propagation of the vector R(k) the phase of the wave ψr is equal to kR and changes only when the magnitude of the vectors k, R changes. At the point of reflection modules of vectors k, R do not changes. This view is held in [17] [18] where the formation of a standing wave is considered. It is shown that for the formation of a standing wave, the reflected wave without changing its phase is added to the incident wave or subtracted from (amplitude changes sign on (-) if the phase of the reflected wave is changed by π).
The direction of vector R is given by the initial condition―the exit angle of the ray from the source. In a homogeneous isotropic medium the direction of R remains unchanged. In inhomogeneous environments, it changes. Besides the length of the vector R continues to grow. The amplitude of the oscillate velocity of the fluid particle is a vector quantity. A direction of vector A in (1) of particle velocity coincides with the direction of propagation of the wave, so a sound wave is a longitudinal wave. When the direction of the vector R, changes by reflection and vector direction A, representing the amplitude of the particle velocity of fluid change too. But any change of the phase of the wave does not occur, as shown above.
In many studies, it is postulated that the change in direction of one of the components of the vector R, for example, Rz upon reflection, changes the sign of the corresponding component of the SP in ψr. That it is not so, shown above. If this mistake do not eliminate then this error will lead to the following: the coordinates (x, z) of R are not equivalent in determining the length of the vector of the reflected wave. With increasing z length R decreases, which contradicts the definition of module R. This leads to incorrect calculation of the phase of the wave. Perhaps individual authors assumed that after the turning point of trajectory the sign of the vertical component of the vector R is inverted, but the sign of the z-component of the vector k remained unchanged. Then, owing to the symmetry trajectories with respect to turning points the phase advance along the trajectory is reduced only to the phase shift along the horizontal distance. The vertical displacements of the trajectory have different signs and compensate each other. In such calculation of phases of the waves caustics do not form. Phases of rays leaving the source at different exit angles will be determined only by the length of their cycle, and at their intersection never coincide.
Another typical error appears when the phase of plane running wave R(x, z) write as a function of a single coordinate. The purpose of this transformation is to show at the example of a plane wave that the wave propagation direction is contained in the spatial part of the phase ψr. Consider this error in details. Let us assume that a plane wave propagates along the axis x. Since the x-axis is a vector, we introduce the unit vector n along the axis x, which takes two values, ±1, for different directions of the vector R = X along axis x. Vectors k and R can be written as: , x0, x―the initial and current coordinates of vector X, k = knk, nk = n. Phase plane wave is
, x0, x―the initial and current coordinates of vector X, k = knk, nk = n. Phase plane wave is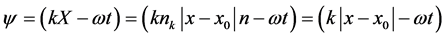 , where
, where ―length vector X, k―vector length k, positive values, and nnk = 1 because the vectors k, X parallel for the any direction of propagation of wave. It is evident that kX does not depend on the direction of wave propagation, modules vectors n, nk not occur in it. In the literature known to us the initial coordinate of the vector X is usually do not indicate. This means that x0 = 0, X in this case is the radius-vector. Start point of any vector must exist or it is can not to determine its length. Phase of a plane wave at x0 = 0 has the form:
―length vector X, k―vector length k, positive values, and nnk = 1 because the vectors k, X parallel for the any direction of propagation of wave. It is evident that kX does not depend on the direction of wave propagation, modules vectors n, nk not occur in it. In the literature known to us the initial coordinate of the vector X is usually do not indicate. This means that x0 = 0, X in this case is the radius-vector. Start point of any vector must exist or it is can not to determine its length. Phase of a plane wave at x0 = 0 has the form: 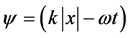 and is the phase of plane waves propagating in both positive and negative x-axis direction from one point x0 = 0. Any difference in the recording phases of these waves is absent. Hence, in particular, it is seen, that these waves will never meet one another and do not create a standing wave. In the literature, see for example [13] , the phase of the wave coming from the point x0 = 0 in the positive direction of the x―axis is wrote as:
and is the phase of plane waves propagating in both positive and negative x-axis direction from one point x0 = 0. Any difference in the recording phases of these waves is absent. Hence, in particular, it is seen, that these waves will never meet one another and do not create a standing wave. In the literature, see for example [13] , the phase of the wave coming from the point x0 = 0 in the positive direction of the x―axis is wrote as: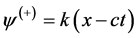 . In this recording, as shown above, must stand |x| when module k is removed out of the brackets, because second phase term
. In this recording, as shown above, must stand |x| when module k is removed out of the brackets, because second phase term 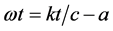 scalar and a positive value. You can add only similar quantities or vectors or scalars. In [13] it is believed that when the wave moves in the direction of negative x, (x = − |x|), then
scalar and a positive value. You can add only similar quantities or vectors or scalars. In [13] it is believed that when the wave moves in the direction of negative x, (x = − |x|), then , here x > 0 or x = |x|. Changing the sign of x means that it is considered as a vector. These two phases
, here x > 0 or x = |x|. Changing the sign of x means that it is considered as a vector. These two phases 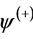 and
and 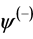 are considered in [13] as phases of plane waves that move in opposite directions. Based on the expressions for the phase plane waves in the solution of the wave equation there is introduced new coordinates
are considered in [13] as phases of plane waves that move in opposite directions. Based on the expressions for the phase plane waves in the solution of the wave equation there is introduced new coordinates 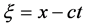 and
and 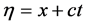 in the wave equation. It does not take into account that the wave with the phase
in the wave equation. It does not take into account that the wave with the phase 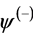 is not a running wave, phase
is not a running wave, phase  is not invariant. As shown above the phase of the running wave is always or constant or zero. Error in the recording phase of the wave leads to that the function
is not invariant. As shown above the phase of the running wave is always or constant or zero. Error in the recording phase of the wave leads to that the function 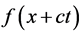 is the solution the wave equation. It does not satisfy the motion equations of fluid, as noted in [8] [9] . Thus, the solution of the wave equation in the form
is the solution the wave equation. It does not satisfy the motion equations of fluid, as noted in [8] [9] . Thus, the solution of the wave equation in the form 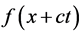 is not a running wave, does not satisfy the motion equations of fluid and cannot be used in acoustics.
is not a running wave, does not satisfy the motion equations of fluid and cannot be used in acoustics.
Consider the typical mistakes when sound waves record with complex variables. In [15] [16] , the function F(z) present in complex form:

F(z) satisfies the wave equation and describes, by the authors opinion, two waves that propagate perpendicular to the waveguide axis x and along z-axis in opposite directions: Another form of writing F(z) is follow:
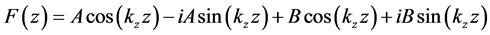
It is seen from the second form of writing F(z) that the sign (-) in the exponent has no relation to the wave’s phases (kzz). Introduction of complex values make to simplify the calculations and is always accompanied by the explanation that the operations with complex values must be linear. After calculations, it is need to retain only the real part of values. Without making any calculations, we write the real and imaginary parts of the two waves F(z) separately, and see how contrary propagation of waves along the z coordinate in the waveguide is expressed:
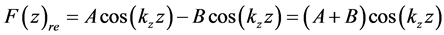 ,
,
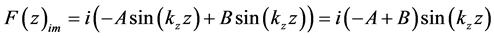 .
.
According to [19] , the sign in the exponent of the complex function determines the sign of the imaginary part of the function F(z). Therefore, the sign in the exponent has no relation to the phase (kzz). Both terms F(z) represent the same function, but the authors [15] [16] believe that they represent waves running in opposite directions. It is known that according to [14] , (kzz) is a part of SP parallel vectors k, r. Their projections at any coordinates x, z is always the same sign, and their product―a positive value. Thus, F(z)re contains no sign propagation z―components of the sound waves. This error appears in many studies and is caused by the mistaken belief what are complex quantities. As noted above, if the function F(z) is the vector functions, A and B are vectors, and may have various destinations, including opposed but their cosine arguments remain the same.
All these attempts to put in a phase wave her propagation direction due to a misunderstanding what is this oscillatory process. Physical definition of the oscillate functions contains in its amplitude. This may be, for example, displacement, compression, temperature, vector or scalar. The amplitude of the oscillate function and its direction, if it is a vector, are determined only by the initial conditions of the problem. Oscillatory part is described by the 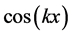 or
or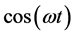 , varying in the same range, from 1 to −1, regardless of the variables, in which their phases are expressed.
, varying in the same range, from 1 to −1, regardless of the variables, in which their phases are expressed.
Let us summarize what has been said. Representation of sound propagation in fluid in the form of a running sound wave (1) is universal, applicable in any medium and for any type of waves emitted by the source. Fluctuations the pressure and velocity of liquid particles compute along a direction of vector R (or in any time) so as the corresponding phase of the sound wave changes. Accuracy of the calculation at each point R is determined only by the accuracy of the knowledge characteristics of environment. If the environment changes over distances less than the half of the wavelength the amplitude of the wave and its phase alter not significantly. Then under these conditions, we can assume that the oscillatory process is not broken. Accuracy of calculation of the pressure and velocity oscillations can be considered sufficient. This condition is not related to the type of source, creating wave of sound in liquid with its wave front. In an inhomogeneous medium wave front changes because direction the vector R transforms (change its configuration). Therefore, when the field is calculated in the inhomogeneous medium, the angular width of the rays must be choosen so as to obtain accurate account.
3. The Vertical Structure of the Sound Field in the Waveguide
It is known that trajectory of rays create a complex structure of the sound field in a waveguide with a depth-dependent velocity of sound. Its main feature is a periodic change of the vertical coordinates of rays as a function of the horizontal one, and its dependence on exit angle of the ray from the source. As a result, in the waveguide forms a set of periodic functions with different periods (cycle length). It is difficult to imagine that a continuous set of periodic functions can create an ordered structure. The most complete picture of the spatial pattern of rays in inhomogeneous waveguide can be obtained if we consider all the rays simultaneously. This is possible if the vertical coordinates of all rays calculate at a fixed horizontal distance from the source with different exit angles. This way of looking at the ray structure of the sound field is applied partially in [1] and in [3] -[8] . Subsequently, the resulting distribution will be called angular distribution (AD) of ray’s coordinate at a fixed distance from the source: Z(θ, x = const), where θ―ray’s exit angle from the source, the individual characteristic of each ray.
Consider the underwater sound channel (USC) with the canonical distribution of the sound velocity with depth. We assume that the waveguide depth H = 4 km depth, USC axis z0 = 1 km, where the speed of sound is minimal. Harmonic point source of sound with radiation frequency ν = 233.6 Hz is placed on the axis of the waveguide z0. The calculation was performed for water rays in waveguide, i.e., the reflected rays from the waveguide boundaries are not considered. The ocean is axial symmetric. Because of it let us assume that the plane of incidence of the sound wave is a vertical plane (x, z), where x and z―horizontal and vertical coordinates of the waveguide. At numerical calculation axis z let be discrete one, the step (size of the discrete point) Δz = 0.25 m. Angular range of water rays divided so that each discrete point below the axis of the waveguide is the point of inversion of one ray. Dependence of the speed of sound c(z) on the depth as a rule is not symmetrical function with respect to the waveguide axis. Gradients c(z) above and below the axis of the waveguide are different. Depth turning of each ray happens above the axis of the waveguide at the point where the sound velocity is equal to its speed of sound in the turning point below the axis z0. Exit angles of rays from the source determine according to Snell’s law: the ratio of the sound velocities at a depth of the source and at the turning points. Since the speed of sound is a nonlinear function of depth exit angles of rays are not equidistant. Assume that the amplitude of the sound field of each ray is equal to the difference of angles of the output of adjacent rays, i.e. angular width of the ray. In [8] it is shown the wave amplitude A(θ) as a function of the exit angle θ, expressed in degrees, multiplied by 103. The angle θ is measured from the axis z. A greatest amplitude A(θ) have rays that are close to horizontal, θ―90˚, since near the axis of waveguide the gradient the velocity of sound is minimal, angular distance between turning points of rays sufficiently large. With a decrease in the exit angle of the sound wave velocity gradient increases, A(θ) decreases. At the lowest value of the exit angle of water rays, θ―77˚, A(θ) is reduced by about 3 times compared with θ ~ 90˚. In [8] , it is shown that the conditions of applicability of geometrical acoustics, [13] , are fulfiled for the canonical type waveguide at a selected frequency radiation.
As follows from the calculation of caustics in [3] -[8] , there is no fundamental difference between the caustics formed by rays which exit from the source to the surface or bottom side, and located above or below the axis of the waveguide. Let us calculate the caustics created by rays, walked toward the bottom, in the first convergence zone at a distance x from 43 to 70 km
Figure 1 shows the eight curves AD Z(θ, xi), calculated at the same distances xi from a source as in [8] , x1 − x8: 43, 46, 48, 51, 55 , 60, 65, 70 km . In this paper, in contrast to [8] , each ray angle of turn up is the angle of full internal reflection (FIR). Above Figure 1 and left side of z-axis are the numbers of curves 1 - 8 corresponding to the above distances from the source. Ray’s coordinates in the scale of figures represent well-ordered structure,
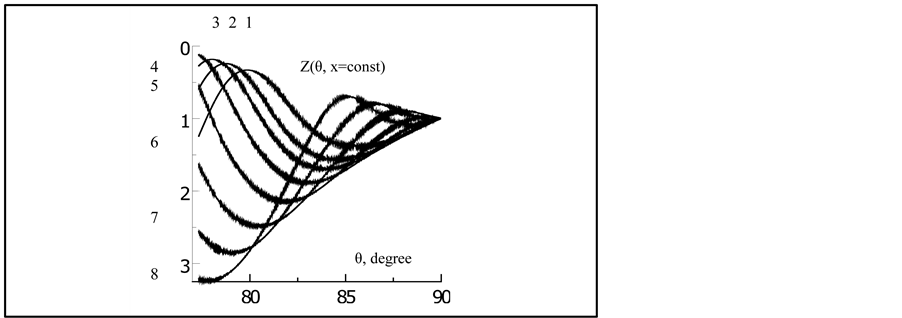
Figure 1. The angular dependence of the ray’s vertical coordinates.
continuous curves. Each curve corresponds to its own distance from source. Each point of each curve determines the depth of one ray at a suitable distance xi. Common to all curves is existence the extrema above and below of the waveguide at a certain depth zic formed rays with different exit angles. With increasing distance xi decreases exit angle θ, in which extremes form, and the extremum is removed from the axis of the waveguide. Extremes of AD Z(θic, xi) are the centers of caustics, θic―center angle of the caustic at a distance xi. Confirmation of this is given below.
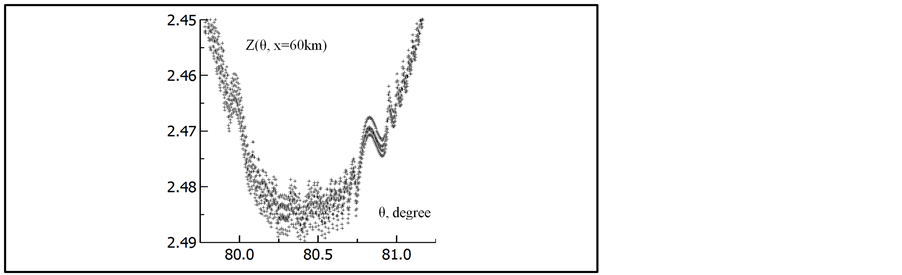
Let us evaluate the replacement of the horizontal section of the trajectory where the inversion occurs at θ = 90˚, to a part of the trajectory with angle FIR. On Figure 2, it is shown two curves at x6 = 60 km, calculated taking into account the angle of FIR, thickened curve 2, and the thin curve 1, from [8] , where the turn angle θ = 90˚, the same for all rays.
Unlike curve 2, taking into account the angle FIR, from curve 1, obtained in [8] , is the appearance of caustic above the axis of the waveguide (Figure 1, curve 6) and a slight increase in the depth of the center of the caustic at the bottom and a slight decrease exit angles of the rays forming this caustic. Others differences on this scale is not visible.
It is clear that the function of AD z(θ, xi), calculated in points, between xi and xi+1 occupy an intermediate position between AD for xi and xi+1. Figure 3 shows the boundary line (BL) in the plane (x, z), formed with coordinates centers of caustics, located below the axis of the waveguide and defined with help of AD from Figure 1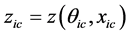 , each point-square. Dots in Figure 3 designate centers of caustics from [8] . It can be seen that the difference between the curves is small.
, each point-square. Dots in Figure 3 designate centers of caustics from [8] . It can be seen that the difference between the curves is small.
BL has a slight inclination to the axis of x, its shift towards the bottom is ~2.3 km in distance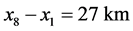 . The size of the region along the z axis of the caustic will be given below.
. The size of the region along the z axis of the caustic will be given below.
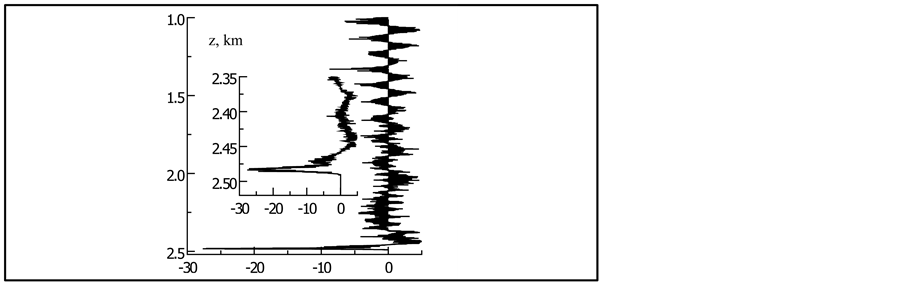
It is of interest to determine what the character of the sound field along vertical of the waveguide at fixed horizontal distance from the source. That field creates with group of rays, that form one curve in Figure 1. Field, calculated by Formula (1), is shown in Figure 4 according to curve 1 from Figure 2. In Figure 5, it is shown the field according to curve 2 from Figure 2.
Vertical line in Figures 4 and 5 plotted depth toward the bottom of the waveguide, starting from its axis, where source is located, horizontal line—the amplitude of the sound field. The scale of the field amplitudes in Figures 4 and 5 differ ~2 times. It is seen that along the entire depth of the waveguide, starting from its axis, the field consists of a number of extrema forming quasi-periodic structure. Ends of both curves are peaks (maximum) amplitude, beyond it there is a shadow zone, the area where the sound field is absent. Coordinates these peaks― the coordinates of the centers of caustic on their BL. The insets in the figures it is shown the field near BL on a larger scale. They show that the depth of the last dots in Figure 4 is the points that create maximum field (peak) at BL. At Figure 5, there are rays with coordinates are greater than the depth of the peak maximum, but its amplitudes is smaller. The shadow area does not appear immediately behind the peak at BL and has a certain transition range. If we take into account that the peak width in Figure 5 is much larger than in Figure 4, we can conclude that the change the method of calculating the trajectories did not change the number of rays forming BL caustic, but they take some more space in depth, width BL more than in Figure 4, and the amplitude is less about two times respectively. A similar distribution of the field along the z axis is observed at other distances xi.
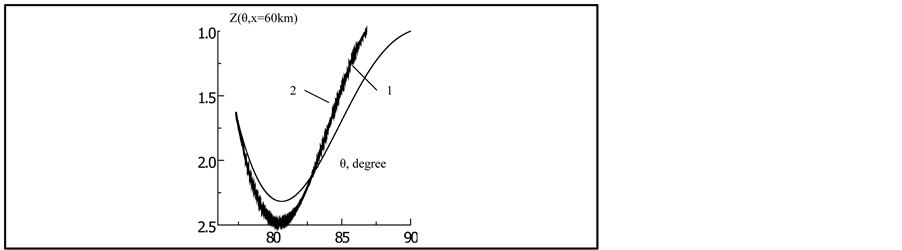
Figure 2. Z(θ, x), thin curve inversion angle rays 90˚, thickened―the angle of total internal reflection.
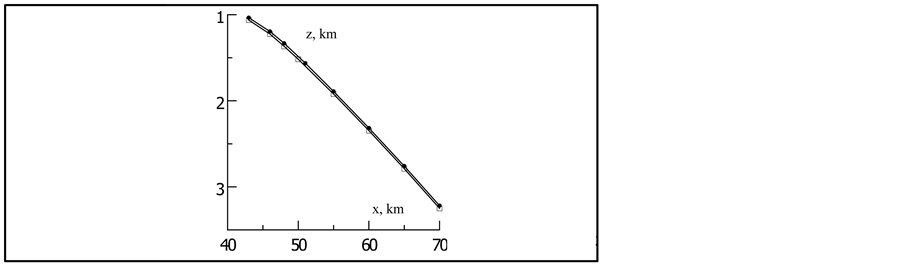
Figure 3. The boundary line of the caustic on plane (x, z), built with caustic centers.
Thus, in various methods of defining points of inversion water rays, rays at a fixed horizontal distance from the source form a well-ordered structure of the quasi-periodic sound field along the axis z. The last point of the field distribution in the depth is the maximum amplitude, deeper this point the sound field is either absent or decreases to zero at the maximum width that actually determines the width BL of the caustic.
4. Features of the Structure of Caustics
Investigate the structure of caustics, when ray’s turning angles 90˚ is changed at the angles FIR.
Figures 6, 7 shows the area of caustics curves 1 and 2 from Figure 2 at a large scale. The main feature of them is preserved angular symmetry. In both figures, there is exit the angle which can be called the center of symmetry of the caustic. At Figure 6, it is seen the AD of caustic, curve 1 from Figure 2. On both sides of her center rays form a strictly ordered symmetric structure: in every point of the depth come a certain number of rays. It is seen that the number of rays in each calculate point away from the center of the caustic decreases. Rays at each point z have close, but different output angles, the angular sector of a source. At the center of the caustic, θ6c = 80.5890, at depth of z6c = 2.31750 km to 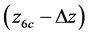 hit 96 rays. Angle difference output extreme rays that form the center of the caustic, is ~0.10, the difference between their arrival times Δt = 0.35 ms, which is ~10 times smaller than the period of the emitted signal τ—4 ms. So at each point z above the center of the caustic hits two groups of rays. These groups locate substantially symmetrically about its center θ6c. It means that each point of the caustic near its center is the focus of the rays with the same (close) phases. Focus size along the z-axis is Δz, the distance between the count points. At each point of the caustic along the z axis the total value of the field should be proportional to the number of intersecting rays if their phase difference is less than π. This is done with sufficient accuracy in the center of the caustic and near it. Thus the amplitude of the field in the center of caustic in Figure 6 is ~60 and formed by 96 rays whose amplitudes ~0.7.
hit 96 rays. Angle difference output extreme rays that form the center of the caustic, is ~0.10, the difference between their arrival times Δt = 0.35 ms, which is ~10 times smaller than the period of the emitted signal τ—4 ms. So at each point z above the center of the caustic hits two groups of rays. These groups locate substantially symmetrically about its center θ6c. It means that each point of the caustic near its center is the focus of the rays with the same (close) phases. Focus size along the z-axis is Δz, the distance between the count points. At each point of the caustic along the z axis the total value of the field should be proportional to the number of intersecting rays if their phase difference is less than π. This is done with sufficient accuracy in the center of the caustic and near it. Thus the amplitude of the field in the center of caustic in Figure 6 is ~60 and formed by 96 rays whose amplitudes ~0.7.
Caustic Figure 7 is less orderly, obviously due to the difference of angles FIR rays, but the angular symmetry of the caustic preserve. Angle difference output rays forming the center of the caustic in Figure 7 ~0.50, i.e. greater than the width of the caustic at 5 times in Figure 6. This means that p(x, z) changes at ≈0.01 of its value only.
Consider the distribution of rays in the caustic for curve 2 of Figure 2. The amplitude at the CC at Figure 5 consists of two maxima. Each maximum hits ~30 rays. The total number of rays at two maxima is nearly equal to the number of rays in Figure 4. This distribution of the number of rays between the two maxima in Figure 5 led to reduction of the field amplitude ~twice. Point, which gets 2 or 6 rays, are located above CC z6c at 50 - 60 m. Their phase difference is more than π, and Δt—10 ms, which exceeds the period τ. These rays can be regarded as the boundary rays of the caustic and put the caustic extension along axis z.
In [8] , it is shown that the rays in the caustics represent a particular the angular sector of water rays of wave front of the source. Chain of focuses along the z-axis determines the area of the caustic along the z-axis and the part of the wave front source, creating a caustic. When distance from the source increase there are new chains of focuses along the axis z create with different angles exit, that continue BL of caustic.
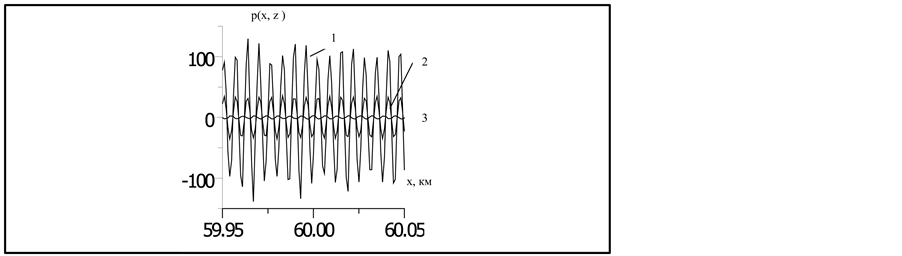
It is interesting to calculate the spatial structure of the sound field along BL caustic. Every point of BL is the sum of rays forming the focus. This calculation is performed for caustics with angle distribution (AD) ray’s vertical coordinates for x6, Figure 2. Their caustics are shown at Figures 6, 7. The sound field p(x, z) are shown at Figures 8, 9 for the for curves 1 and 2 from Figure 2. The vertical axis shows the amplitude of the field, along the horizontal―the distance x from the source. The x coordinates in Figure 8 are symmetric with respect to the caustic’s centre, Δx = x6 ± 50 m, z = z6c. Field p(x, z) is calculated at three depths, curve 1―along BL, where p(x, z) has the greatest value, 2―above BL 1 m, z = z6c − 1 m, 3 above 50 m, z = z6c − 50 m, the minimum value of the field p(x, z). It is seen a clear periodic structure of the sound field p(x, z) as a function of x for all the three depths. Wavelength is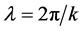 . This indicates that the rays forming the field at every point (x, z) looking curves, have the same phases, but different angles out of the source and the different propagation paths. Coincidence of phases is explained by that the ray path length difference is compensated by the difference in the velocities of propagation: the greater path length ((deeper point inversion), the greater the speed of sound. The number of rays N that form the field along the caustic BL in Figure 8, is ~100. At a distance from the BL at 1 m N - 39 - 35, removing 50 m N ~ 6―Amplitude of the field (the angular width of ray) carried by each ray forming this caustic, somewhat less than 1. Figure 8 shows that the total value of the field along each curve at a fixed depth is proportional to the number of rays, forming it. Sound field phase curves 1 and 2 coincide, and curve 3 is the field has a shift ~π to the first two. This may be caused by a change of the wave vector k of the module away from the center of the caustic at 50 m, which led to a change in the phase difference the value of ~π between along the field lines BL and shifted by 50 m away. Saving frequency fields and proportionality of the value of the field the number of rays confirms equal phases of the individual rays forming foci’s caustic. At Figure 9, the field along BL caustic, curve 1, is obtained based angle FIR. As in Figure 8, it is also a periodic function the same period, whose amplitude varies slightly.
. This indicates that the rays forming the field at every point (x, z) looking curves, have the same phases, but different angles out of the source and the different propagation paths. Coincidence of phases is explained by that the ray path length difference is compensated by the difference in the velocities of propagation: the greater path length ((deeper point inversion), the greater the speed of sound. The number of rays N that form the field along the caustic BL in Figure 8, is ~100. At a distance from the BL at 1 m N - 39 - 35, removing 50 m N ~ 6―Amplitude of the field (the angular width of ray) carried by each ray forming this caustic, somewhat less than 1. Figure 8 shows that the total value of the field along each curve at a fixed depth is proportional to the number of rays, forming it. Sound field phase curves 1 and 2 coincide, and curve 3 is the field has a shift ~π to the first two. This may be caused by a change of the wave vector k of the module away from the center of the caustic at 50 m, which led to a change in the phase difference the value of ~π between along the field lines BL and shifted by 50 m away. Saving frequency fields and proportionality of the value of the field the number of rays confirms equal phases of the individual rays forming foci’s caustic. At Figure 9, the field along BL caustic, curve 1, is obtained based angle FIR. As in Figure 8, it is also a periodic function the same period, whose amplitude varies slightly.
At a distance of 1m from the BL, (thicken line) curve 2, the field has a quasi-periodic, but retained the amplitude close to the amplitude at the BL. At a distance of 50 m from BL field is not periodic, but its amplitude is greater than the amplitude of the field at the same distance in Figure 8. Based on Figure 9 can be inferred that the phases of the rays forming the BL caustic at each focus at least partially coincide. At a distance from the BL caustic along the z axis overlap phases preserved, as evidenced by the larger amplitude of the field with mowing off the BL than in Figure 8.
Let us compare the field wave front (WF) of a point source in isotropic medium and field along BL caustic produced in the USC. Form propagating WF in homogeneous medium do not changes. At a case of USC ray paths (vectors R), depend on the exit angle. Separate groups of rays with close exit angles and equal phases form foci. Thus each focus is the little part (angular sectors) of WF, has his own propagation time and coordinates at BL. Consequently, the line of caustic as the spatial structure of the periodic sound field with a wavelength of 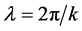 is analogous to the propagation of sound waves along the radius in a homogeneous medium. We can assume that along BL extends a running wave formed with foci whose coordinates are changing with the speed of sound wave propagation.
is analogous to the propagation of sound waves along the radius in a homogeneous medium. We can assume that along BL extends a running wave formed with foci whose coordinates are changing with the speed of sound wave propagation.
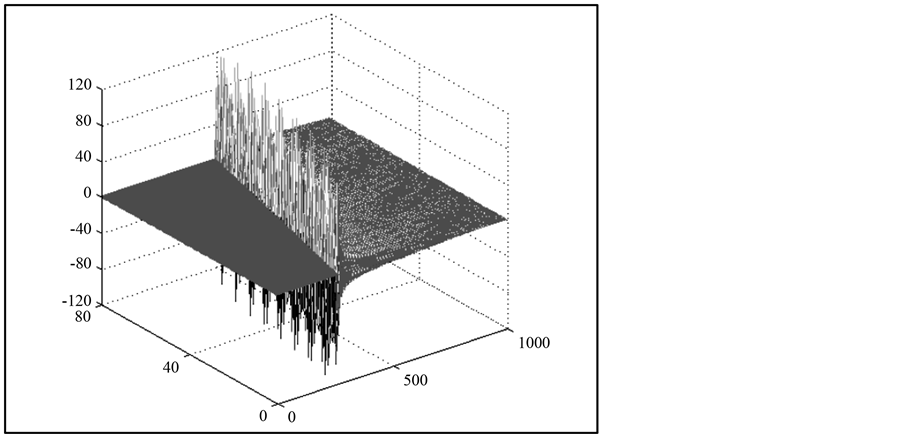
Let us calculate the spatial structure of the sound field in the plane (x, z). The method of calculation of the field dependence of the two coordinates is as follows. AD calculation is carried out along the z axis in a sequence of points , where
, where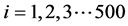 . The interval between the points account Δx along the x axis is assumed to be 1 meter, which provides a satisfactory transmission periodic spatial structure of the field. Figure 10 shows the spatial distribution of the amplitude of the sound field in the region of the caustic as a function of the coordinates x, z, calculated in [8] .
. The interval between the points account Δx along the x axis is assumed to be 1 meter, which provides a satisfactory transmission periodic spatial structure of the field. Figure 10 shows the spatial distribution of the amplitude of the sound field in the region of the caustic as a function of the coordinates x, z, calculated in [8] .
X coordinate varies in the range from x6 − 500 m, up to x6 + 500 m (axis points 0 - 1000), where x6 = 60 km.
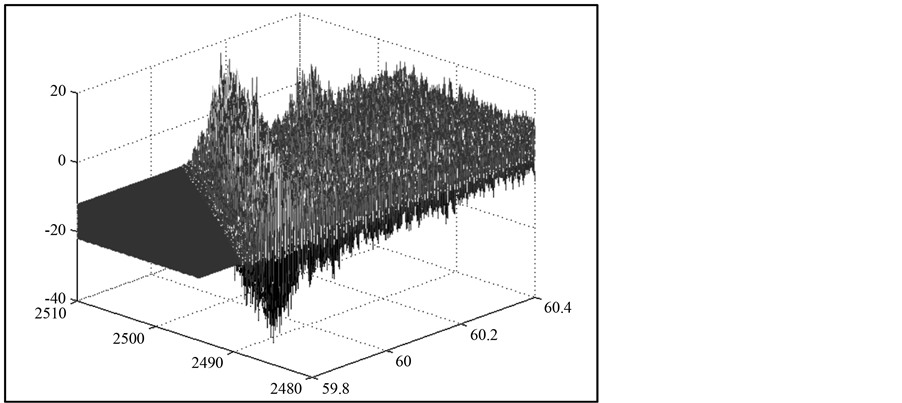
Depth z varies in the range 2.298 - 2.318 km (axis points 0 - 80), where z6c = 2.3175 km. The vertical axis of the Figure 10 (axis points −120, 120) according Figure 8 is the amplitude of the sound field. Left of the BL field is equal to 0, the shadow zone, where the sound waves do not get. Right from the BL field amplitude decreases sharply. Figure 11 shows space structure caustic (Figure 7), calculated taking into account the angle of FIR rays.
Coordinate axes are follow: x = 59.8 − 60.4 km (number points 600), z = 2480 − 2510 m (number points 120).
The shadow zone in this case is also clearly visible. BL caustics also clearly marked, but the field has a chaotic character along it.. BL width considerably greater than in Figure 10, which is consistent with Figures 5, 7. On Figure 11 there is visible one of the side caustic that is present in Figure 7.
5. Conclusions
Results of the study are as follows.
A detailed analysis of typical errors in definition of a spatial phase of the running sound wave is done. Their elimination allows you to calculate the phase of wave on the direction of propagation correctly.
It is found that the boundary line in the region of the caustic consists of a row of foci of groups of rays with closed exit angles and equal phases. Each focus represents a single area of wave front water rays source and has its own time propagation in an inhomogeneous medium.
In a inhomogeneous medium a united wave front all rays are absent. Along the boundary line of the caustic is a sequential propagation of ray groups representing angular sectors focused wave front of the source. Equal propagation time have only the rays that form one focus.
Sound field along the boundary line of the caustic is a periodic function. His wavelength is the same as wavelength along the radius of the homogeneous medium. Boundary line is due to the dependence of distance (time) from the exit angle of rays from the source. We can assume that the angular dependence of the field in the waveguide is transformed into a temporary (spatial). From this viewpoint, the sound field along the boundary line similarly spread running acoustic wave.
Saving the periodicity of the sound field along the boundary line of caustic shows the following. The calculation of the field by ray method is so precise that there has been no break of its periodic structure. It is possible to calculate the phases of the rays and the sum of their fields at certain points (foci) of the boundary line correctly.
References
- Brekhovskikh, L.M. (1973) Waves in Layered Spaces. M. Science, Moscow, 343.
- Brekhovskikh, L.M. (1974) Ocean Acoustics. M. Science, Moscow, 693.
- Zverev, V.A. and Ivanova, G.K. (2003) On the Formation of Waves Brillouin Underwater Sound Channel. Acoustical Journal, 49, 633-637.
- Zverev, V.A. and Ivanova, G.K. (2005) On the Vertical Structure of the Sound Field in the Canonical Waveguide at Large Distances. Acoustical Journal, 51, 771-776.
- Zverev, V.A. and Ivanova, G.K. (2007) Range Dependence of the Sound Field in the Ocean. Acoustical Physics, 53, 197-204.
- Zverev, V.A. and Ivanova, G.K. (2008) The Horizontal Structure of the Sound Field in the Ocean. Acoustical Physics, 54, 356-362.
- Zverev, V.A., Ivanov, V.P. and Ivanova, G.K. (2010) Calculation of the Sound Field in the Ocean in Caustic Surfaces by the Ray Method. Proceedings of the 22nd Conference of the Russian Acoustic Society, Moscow, 15-17 June 2010 191-194.
- Zverev, V.A., Ivanov, V.P. and Ivanova, G.K. (2011) Caustics in Underwater Sound Channel and Their Connection with the Wave Front of the Point Source. Ocean Acoustics, Proceedings of the 13th L. M. Brekhovskikh’s Conference, Moscow, 31 May-3 June 2011, 49-52.
- Ivanov, V.P. and Ivanova, G.K. (2012) One Aspect of Sound Waves Propagation in Inhomogeneous Water Space. Proceedings of the 25th Conference of the Russian Acoustic Society, Moscow, 17-20 September 2012, 338-341.
- Ivanov, V.P. and Ivanova, G.K. (2013) Some Aspects of Ray Representation Running Sound Waves in Liquid Spaces. Open Journal of Acoustics, 3, 7-13.
- Ivanov, V.P. and Ivanova, G.K. (2013) A New Concept of Calculation of Reflection and Passage Sound Waves on the Boundary of Liquid Spaces. Ocean Acoustics, Proceedings of the 14th L. M. Brekhovskikh’s Conference, Moscow, 17- 21 June 2013, 121-124.
- Ivanov, V.P. and Ivanova, G.K. (2013) A New Concept of Calculation Coefficients of Relection and Passage Sound Waves on the Boundary of Liquid Spaces. Open Journal of Acoustica, 3, 72-79. http://dx.doi.org/10.4236/oja.2013.33012
- Landau, L.D. and Lifshitz, V.M. (1988) Hydrodynamics. Publishing Nauka, Moscow.
- Smirnov, V.I. (1958) Course of Higher Mathematics. State Publishing Physical and Mathematical Literature, Moscow.
- Katsenelembaum, V.Z. (1966) High-Frequency Electrodynamics. Basics Mathematical Apparatus. Nauka, Moscow.
- Lependin, L.F. (1978) Acoustics. Graduate School, Moscow, 448.
- Physical Encyclopedic Dictionary (1966) Standing Waves. Publishing House “Soviet Encyclopedia”, Moscow.
- Khaikin, S.A. (1947) Mechanics. State Publishing House of Techno-Theoretical Literature, Moscow.
- Smirnov, V.I. (1958) Course of Higher Mathematics. State Publishing Physical and Mathematical Literature, Moscow.