Open Journal of Acoustics
Vol. 2 No. 2 (2012) , Article ID: 20456 , 8 pages DOI:10.4236/oja.2012.22010
Vibration Analysis of an Infinite Poroelastic Circular Cylindrical Shell Immersed in Fluid
Department of Mathematics, Deccan College of Engineering and Technology, Hyderabad, India
Email: ahmed_shah67@yahoo.com
Received February 16, 2012; revised March 16, 2012; accepted March 24, 2012
Keywords: Biot’s Theory; Axially Symmetric Vibrations; Radial Vibrations; Poroelastic Cylindrical Shell; Pervious Surface; Impervious Surface; Phase Velocity; Cut-Off Frequency
ABSTRACT
The purpose of this paper is to study the effect of presence of fluid within and around a poroelastic circular cylindrical shell of infinite extent on axially symmetric vibrations. The frequency equation each for a pervious and an impervious surface is obtained employing Biot’s theory. Radial vibrations and axially symmetric shear vibrations are uncoupled when the wavenumber is vanished. The propagation of axially symmetric shear vibrations is independent of presence of fluid within and around the poroelastic cylindrical shell while the radial vibrations are affected by the presence of fluid. The frequencies of radial vibrations and axially symmetric shear vibrations are the cut-off frequencies for the coupled motion of axially symmetric vibrations. The non-dimensional phase velocity as a function of ratio of thickness to wavelength is computed and presented graphically for two different types of poroelastic materials for thin poroelastic shell, thick poroelastic shell and poroelastic solid cylinder.
1. Introduction
Gazis [1] discussed the propagation of free harmonic waves along a hollow elastic circular cylinder of infinite extent and presented numerical results. Bjorno and Ram Kumar [2] presented theoretical and experimental results of propagation of axially symmetric waves in submerged elastic rods. Chandra et al. [3] studied the axially symmetric vibrations of cylindrical shells immersed in an acoustic medium. Employing Biot’s [4] theory, Tajuddin and Sarma [5] studied the torsional vibrations of poroelastic cylinders. Wisse et al. [6,7] presented the experimental results of guided wave modes in porous cylinders and extended the classical theory of wave propagation in elastic cylinders to poroelastic mandrel modes. Chao et al. [8] studied the shock-induced borehole waves in porous formations. Vashishth and Poonam Khurana [9] presented the solutions of elastic wave propagation along a cylindrical borehole in an anisotropic poroelastic solid and derived frequency equations for empty and fluidfilled boreholes. Farhang et al. [10] investigated the wave propagation in transversely isotropic cylinders. Tajuddin and Ahmed Shah [11,12] studied the circumferential waves and torsional vibrations of infinite hollow poroelastic cylinders in presence of dissipation. Ahmed Shah [13,14] studies the axially symmetric vibrations of fluidfilled poroelastic circular cylindrical shells and spherical shells of various wall-thicknesses.
In the present analysis, the axially symmetric vibrations of poroelastic circular cylindrical shells of infinite extent immersed in an acoustic medium are investigated employing Biot’s [4] theory. Biot’s model consists of an elastic matrix permeated by a network of interconnected spaces saturated with liquid. The frequency equation of such vibrations is derived each for a pervious surface and an impervious surface. Cut-off frequencies when the wavenumber is zero are obtained both for pervious and impervious surfaces. For zero wavenumber, the frequency equations of axially symmetric shear vibrations and radial vibrations are uncoupled. Axially symmetric shear vibrations are independent of nature of surface as well as presence of fluid within and around the poroelastic cylindrical shell. The radial vibrations are dependent on nature of surface and these are affected by the presence of fluid within and around poroelastic cylindrical shell. Nondimensional phase velocity for propagating modes is computed in absence of dissipation for cylindrical shells immersed in an acoustic medium each for a pervious and an impervious surface. The cut-off frequency as a function of h/r1 is determined. The results are presented graphically for two types of poroelastic materials and then discussed. By ignoring the liquid effects, and after rearrangement of terms, results of purely elastic solid are shown as a particular case considered by Chandra et al. [3], Bjorno and Ram Kumar [2]. The considered problem is applicable to deep sea sound sources and transducers, petrochemical industries, acoustic waveguides, ultrasonic delay-lines and frequency control devices.
2. Governing Equations
The equations of motion of a homogeneous, isotropic poroelastic solid (Biot, [4]) in presence of dissipation b are
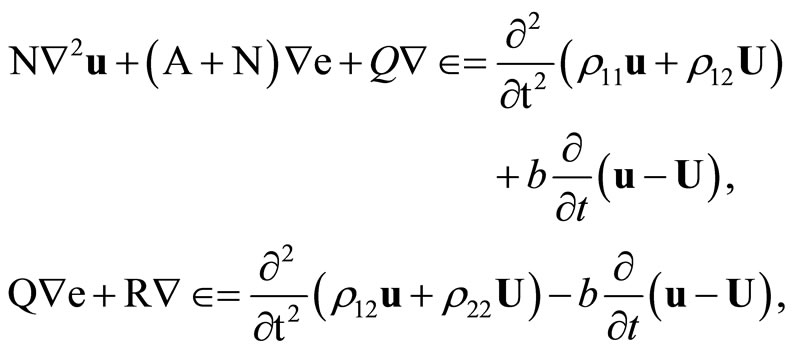 (1)
(1)
where Ñ2 is the Laplacian, 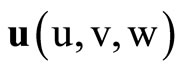 and
and 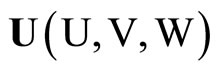 are displacements of solid and liquid respectively, e and Î are the dilatations of solid and liquid; A, N, Q, R are all poroelastic constants and rij (i, j = 1, 2) are the mass coefficients following Biot [4]. The poroelastic constants A, N corresponds to familiar Lame’ constants in purely elastic solid. The coefficient N represents the shear modulus of the solid. The coefficient R is a measure of the pressure required on the liquid to force a certain amount of the liquid into the aggregate while total volume remains constant. The coefficient Q represents the coupling between the volume change of the solid to that of liquid.
are displacements of solid and liquid respectively, e and Î are the dilatations of solid and liquid; A, N, Q, R are all poroelastic constants and rij (i, j = 1, 2) are the mass coefficients following Biot [4]. The poroelastic constants A, N corresponds to familiar Lame’ constants in purely elastic solid. The coefficient N represents the shear modulus of the solid. The coefficient R is a measure of the pressure required on the liquid to force a certain amount of the liquid into the aggregate while total volume remains constant. The coefficient Q represents the coupling between the volume change of the solid to that of liquid.
The equation of motion for a homogeneous, isotropic, inviscid elastic fluid is
 , (2)
, (2)
where F is displacement potential function and Vf is the velocity of sound in the fluid. The displacement of fluid is .
.
The stresses sij and the liquid pressure s of the poroelastic solid given by Biot [4] are
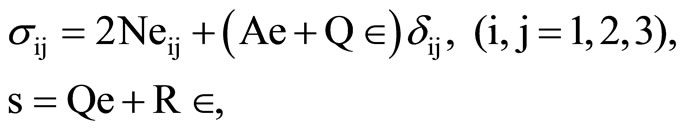 , (3)
, (3)
where dij is the well-known Kronecker delta function.
The fluid pressure Pf is given by
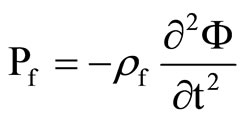 . (4)
. (4)
In Equation (4), rf is the density of the fluid.
 (5)
(5) The subscript “if” or “of” associated with a quantity represents that the quantity is related to inner or outer fluid. For example, Vif is the velocity of sound in the inner fluid and Pof is the outer fluid pressure.
3. Solution of the Problem
Let (r, q, z) be the cylindrical polar coordinates. Consider a homogeneous, isotropic, infinite poroelastic cylindrical shell immersed in an inviscid elastic fluid. Let the inner and outer radii of the poroelastic cylindrical shell be r1 and r2 respectively so that the thickness of shell is h [= (r2 – r1) > 0]. The axis of the poroelastic shell is in the direction of z-axis. The fluid column within the poroelastic cylindrical shell extends from zero to infinity in axial direction and zero to r1 in the radial direction. The outer fluid extends from r2 to infinity in radial direction and zero to infinity in axial direction. Then for axially symmetric vibrations, the displacement of solid 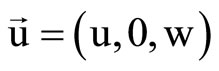 that can readily be evaluated from field Equation (1) is (as shown in the bottom of this page).
that can readily be evaluated from field Equation (1) is (as shown in the bottom of this page).
In Equation (5), w is the frequency of wave, k is wavenumber, C1, C2, C3, C4, A and B are constants, J0(x), Y0(x) are Bessel functions of first and second kind each of order zero, J1(x), Y1(x) are Bessel functions of first and second kind each or order one. Here i is complex unity or i2 = –1 and
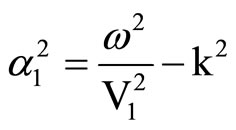 ,
, 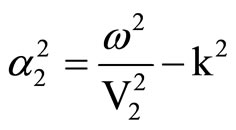 ,
,  , (6)
, (6)
where Vi (i = 1, 2) are dilatational wave velocities of first and second kind respectively, V3 is shear wave velocity.
The displacement of inner fluid column uif = (uif, 0, wif) for axially symmetric vibrations is
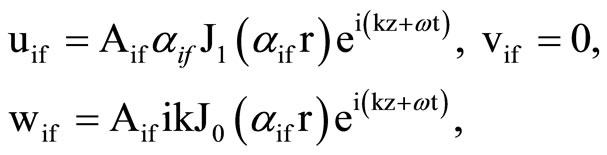 (7)
(7)
where Aif is constant and
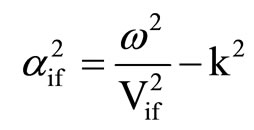 . (8)
. (8)
with the help of displacement potential function, the pressure of the inner fluid column is given by
 , when
, when 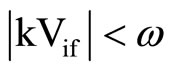 (9)
(9)
Similarly, the displacement and the outer fluid pressure are given by equations

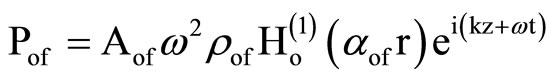 , (10)
, (10)
where Aof is constant, 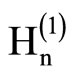 is Hankel function of first kind and order n and
is Hankel function of first kind and order n and
 . (11)
. (11)
For imaginary values of aof, that is, when the phase velocity {w/k} is less than Vof the Hankel function of first kind  is replaced by the modified Bessel function of second kind K0(aofr).
is replaced by the modified Bessel function of second kind K0(aofr).
Substituting the displacement function u and w from Equation (5), fluid pressures from Equations (9) and (10), into Equation (3) together with Equation (7), the relevant displacement, liquid pressure and stresses are
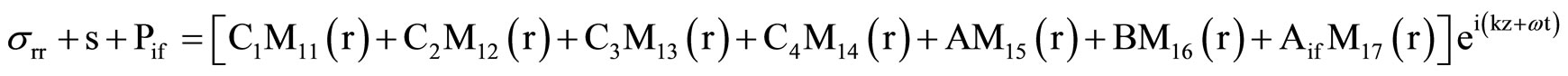 , (12)
, (12) 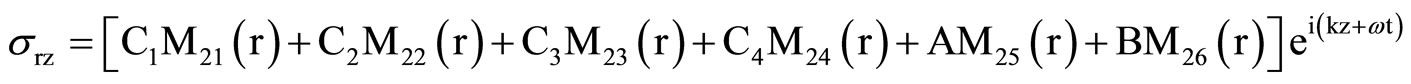 , (13)
, (13)
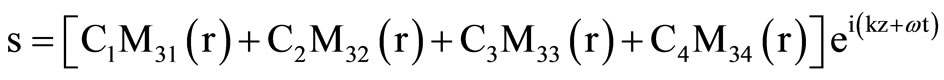 , (14)
, (14)
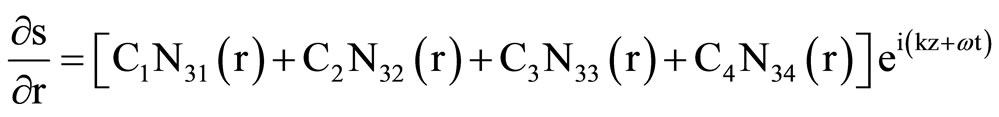 , (15)
, (15)
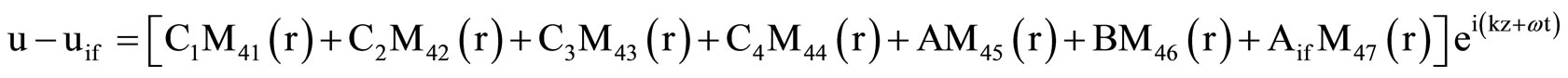 , (16)
, (16) 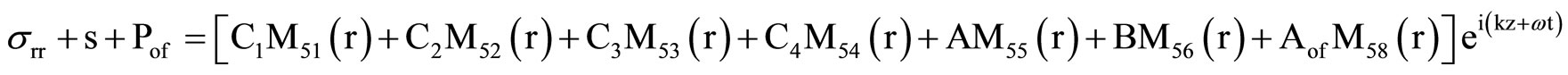 , (17)
, (17)  , (18)
, (18) where C1, C2, C3, C4, A, B, Aif, Aof are all constants and the coefficients Mij(r), Nij(r) are
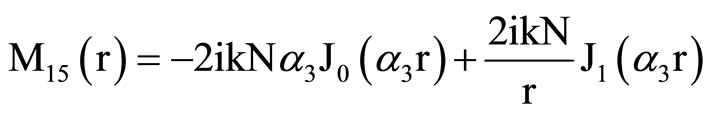
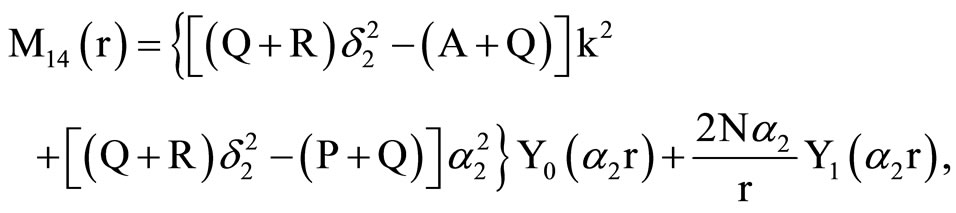
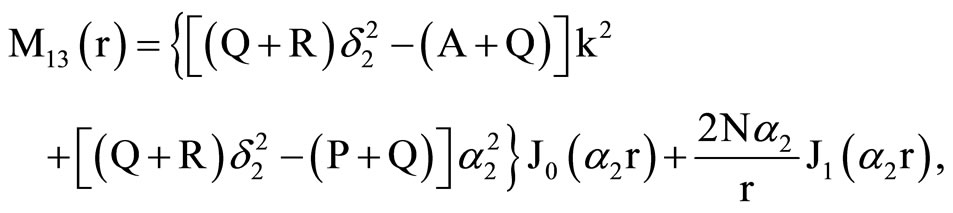
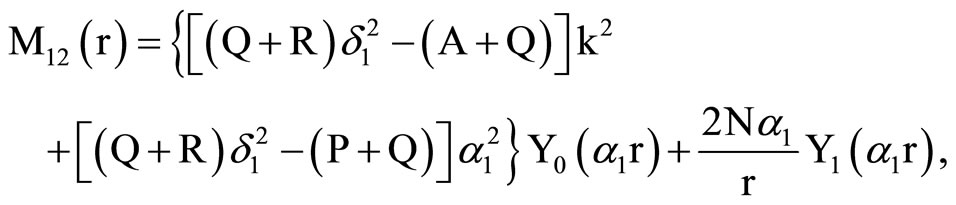
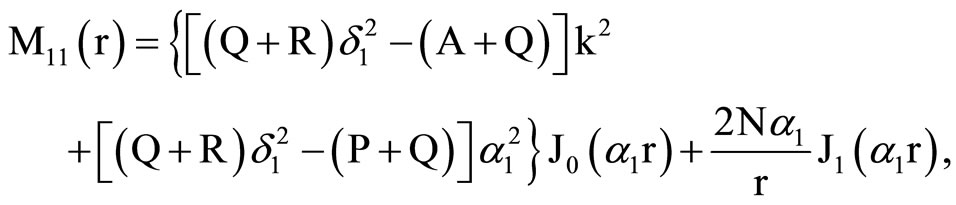 ,
,  ,
, 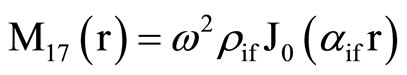 ,
, 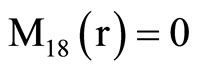 ,
, 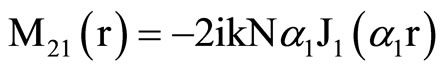 ,
, 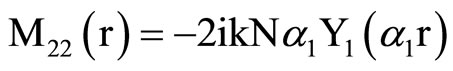 ,
, 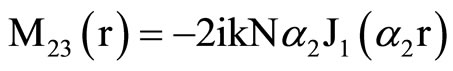 ,
, 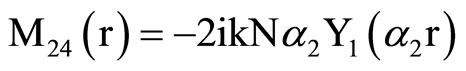 ,
,  ,
,  ,
, 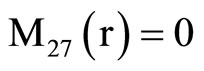 ,
, 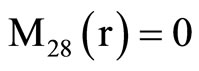 ,
, 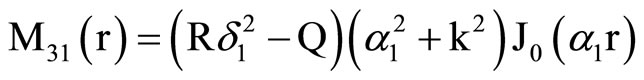 ,
, 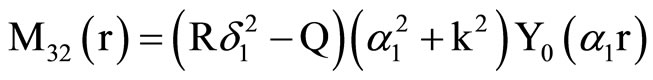 ,
, 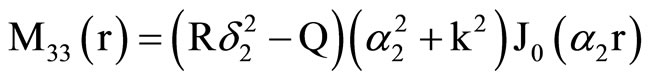 ,
, 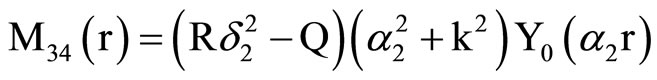 ,
, 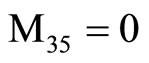 ,
, 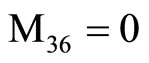 ,
, 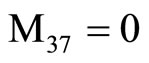 ,
, 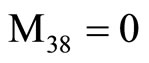 ,
, 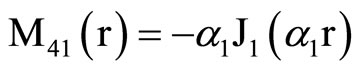 ,
, 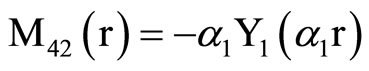 ,
, 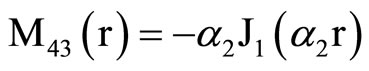 ,
, 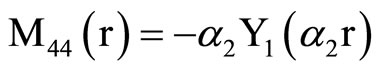 ,
, 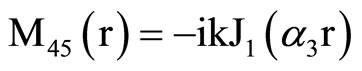 ,
, 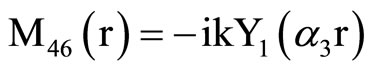 ,
, 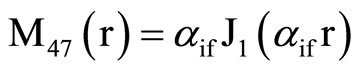 ,
, 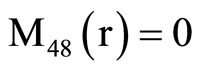 ,
, 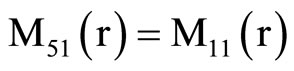 ,
, 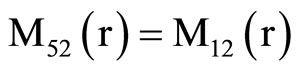 ,
, 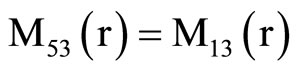 ,
, 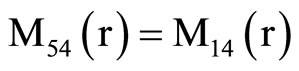 ,
, 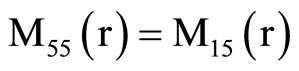 ,
, 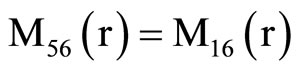 ,
, 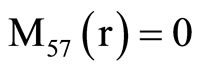 ,
, 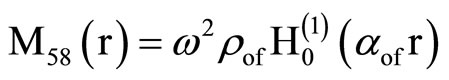 ,
, 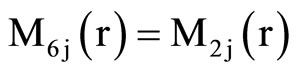 ,
, 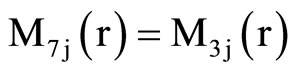 ,
, 
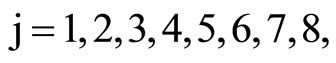 ,
,  ,
,  ,
,  ,
, 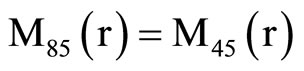 ,
,  ,
, 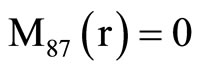 ,
, . (19)
. (19)
In Equation (19), 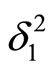 and
and  are
are
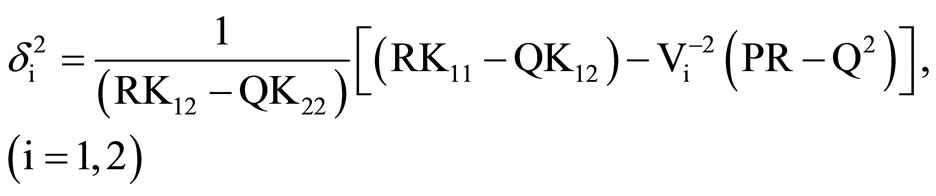 (20)
(20)
P = A + 2N and
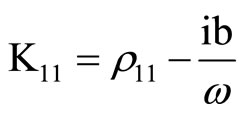 ,
, 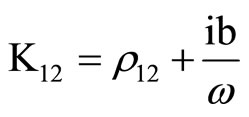 ,
, . (21)
. (21)
4. Frequency Equation
For perfect contact between the poroelastic cylindrical shell and the fluids, we assume that the normal and shear stresses and radial displacements are continuous at r = r1 and r = r2. Thus the boundary conditions in case of a pervious surface are
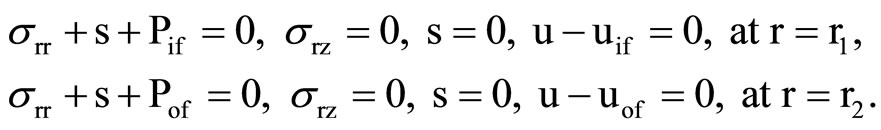 (22)
(22)
The boundary conditions in case of an impervious surface are
 (23)
(23)
Substitution of Equations (12)-(14) and (16)-(18) into the Equation (22) result in a system of eight homogeneous algebraic equations in eight constants C1, C2, C3, C4, A, B, Aif and Aof. For a non-trivial solution, the determinant of the coefficients must vanish. By eliminating these constants, the frequency equation of axially symmetric vibrations of poroelastic circular cylindrical shell immersed in fluid in case of a pervious surface is
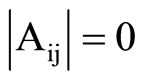 ,
,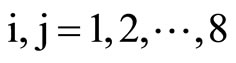 . (24)
. (24)
In Equation (24), the elements Aij are
 (25)
(25)
where Mij(r) are defined in Equation (19).
Arguing on similar lines, Equations (12), (13), (15)- (18) together with the Equation (23) yield the frequency equation of axially symmetric vibrations of poroelastic circular cylindrical shell immersed in fluid, in case of an impervious surface to be
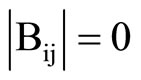 ,
, 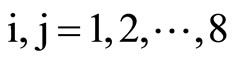 , (26)
, (26)
where the elements Bij are
 (27)
(27)
where Mij(r) and Nij(r) are defined in Equation (19).
By eliminating liquid effects from frequency equation of pervious surface (24), that is, setting b®0, r12®0, r22®0, 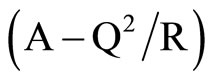 ®l, N®m, Q®0, R®0 and after some rearrangement of terms, the results of purely elastic solid are recovered as a special case considered by Chandra et al. (1976). The frequency equation of an impervious surface (26) has no counterpart in purely elastic solid.
®l, N®m, Q®0, R®0 and after some rearrangement of terms, the results of purely elastic solid are recovered as a special case considered by Chandra et al. (1976). The frequency equation of an impervious surface (26) has no counterpart in purely elastic solid.
4.1. Frequency Equation for Poroelastic Solid Cylinder
When the ratio of thickness to inner radius of the poroelastic cylindrical shell i.e., h/r1®¥ as r1®0 with finite thickness, it reduce to a poroelastic solid cylinder of radius h. Then the frequency equation of a pervious surface (24) is reduced to
 ,
, 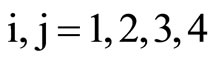 , (28)
, (28)
where the elements Pij are
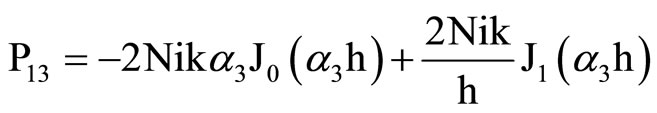
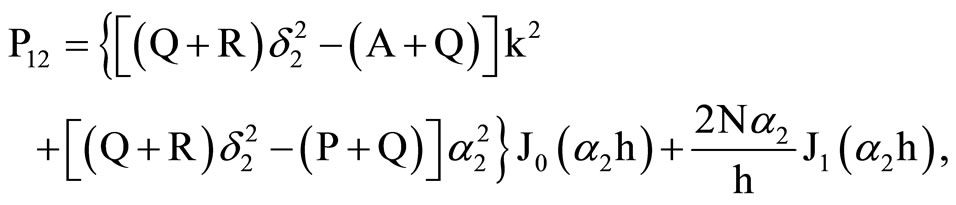
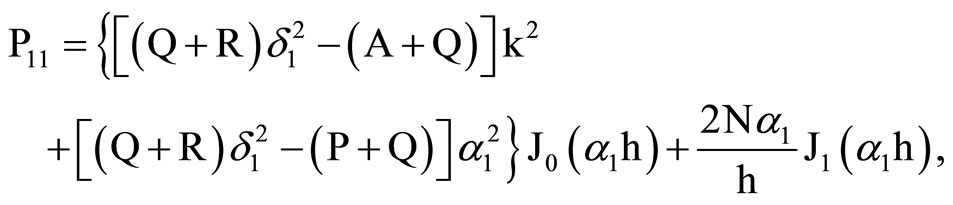 ,
, 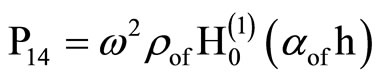 ,
,  ,
, 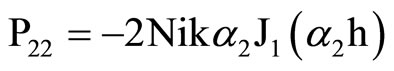 ,
, 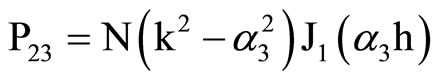 ,
,  ,
,  ,
, 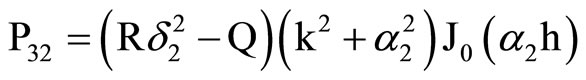 ,
, 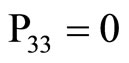 ,
, 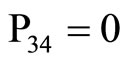 ,
,  ,
,  ,
, 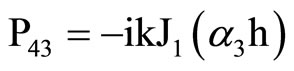 ,
,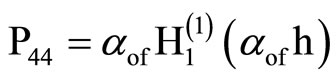 . (29)
. (29)
In Equation (29), J0, J1 are Bessel functions of first kind of order zero and one; ,
, 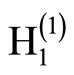 are Hankel functions of first kind of order zero and one.
are Hankel functions of first kind of order zero and one.
Similarly, frequency Equation (26) when r1®0 and finite h, reduce to
 ,
, 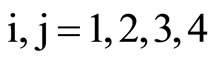 , (30)
, (30)
where the elements Qij are
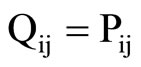 ;
;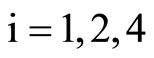 ,
,  , and
, and ,
, 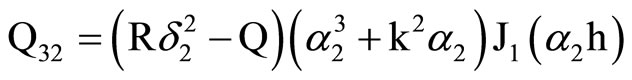 ,
,  ,
,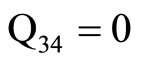 . (31)
. (31)
Equations (28) and (30) are the frequency equations of axially symmetric vibrations of a poroelastic solid cylinder immersed in fluid, for a pervious and an impervious surface, respectively.
By eliminating liquid effects and after some rearrangement of terms in Equation (28), the results of purely elastic solid considered by Bjorno and Ram Kumar (1972) are recovered as a special case. Frequency equation of an impervious surface (30) has no counterpart in purely elastic solid.
4.2. Cut-Off Frequencies
The frequencies obtained by equating wavenumber to zero are referred to as the cut-off frequencies. Thus for k = 0, the frequency equation of pervious surface (24) reduce to the product of two determinants as D1D2 = 0,(32)
where D1 and D2 are
 (33)
(33)
The elements Aij of D1 and D2 are defined in Equation (25) are now evaluated for k = 0. From Equation (32) it is clear that either D1 = 0 or D2 = 0 and these two equations give the cut-off frequencies of axially symmetric vibrations. The frequency equation D1 = 0,(34)
give the frequencies of radial vibrations of poroelastic cylindrical shells immersed in an acoustic medium, for a pervious surface while the frequency equation D2 = 0,(35)
does not depend on fluid parameters, and it give the frequencies of axially symmetric shear vibrations which are independent of presence of fluid within and around the poroelastic cylindrical shell. The radial vibrations are affected by the presence of fluid within and around the poroelastic cylindrical shell while the axially symmetric shear vibrations are not affected as can be seen from Equations (34) and (35).
Similarly, the frequency equation of an impervious surface (26), when k = 0 is reduced to the product of two determinants D3D4 = 0,(36)
where D3 and D4 are
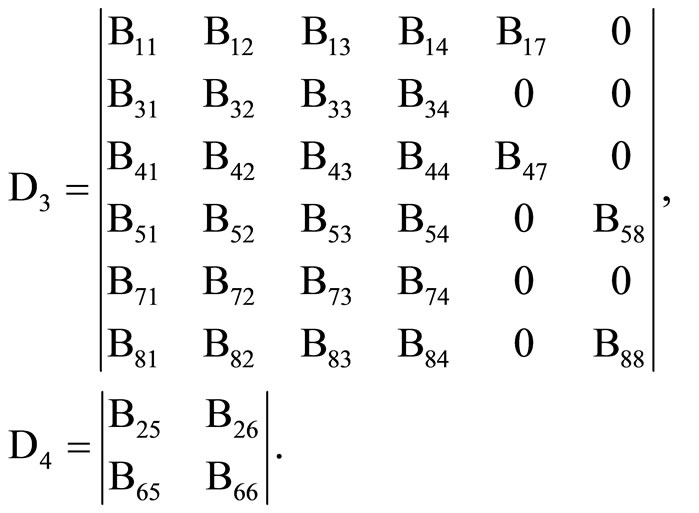 (37)
(37)
The elements appearing in D3 and D4 are defined in Equation (27) are now evaluated for k = 0. From Equation (36) it is clear that either D3 = 0 or D4 = 0. The equation D3 = 0,(38)
corresponds to frequencies of radial vibrations of a poroelastic cylindrical shell immersed in an acoustic medium in case of an impervious surface, while the equation D4 = 0,(39)
yield the cut-off frequencies independent of presence of fluid. Also it is seen that Equations (35) and (39) are same by virtue of Equation (27). Hence Equation (39) is independent of nature of surface, that is, pervious or impervious. Therefore, the cur-off frequencies given by Equation (39) are independent of presence of fluid within and around the poroelastic cylindrical shell and nature of surface, that is, pervious or impervious. Equation (35) is the frequency equation of axially symmetric shear vibrations. From Equation (32), it is clear that the radial vibrations and axially symmetric shear vibrations are uncoupled for poroelastic cylindrical shell immersed in an acoustic medium in case of a pervious surface. Similarly, these are uncoupled for an impervious surface as can be seen from Equation (36). The cut-off frequencies of poroelastic solid cylinder for pervious and impervious surfaces are obtained in a similar way as obtained in case of poroelastic cylindrical shells.
5. Non-Dimensionalization of Frequency Equation
For the purpose of numerical computation we set b = 0, and the wavenumber k is real. The phase velocity C is the ratio of frequency to wavenumber, that is, C=w/k. To analyze the frequency Equations (24) and (26) it is convenient to introduce the following non-dimensional variables:
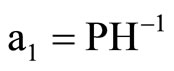 ,
,  ,
, 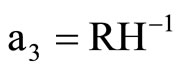 ,
, 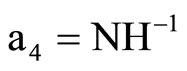 ,
,  ,
, 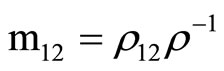 ,
,  ,
, 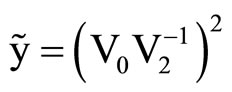 ,
,  ,
, 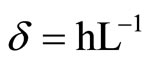 ,
,  ,
,  ,
, 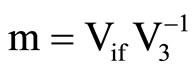 ,
, 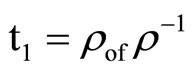 ,
,  ,
, 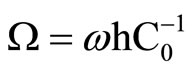 ,
,  ,
, 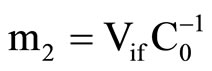 ,
, 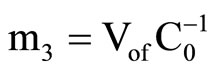 , (40)
, (40)
where W is non-dimensional frequency, x is non-dimensional phase velocity of poroelastic cylindrical shells immersed in an acoustic medium, H = P + 2Q + R, r = r11 + 2r12 + r22, C0 and V0 are the reference velocities (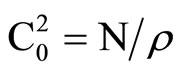 ,
,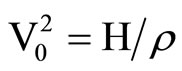 ), C [= w/k] is phase velocity h is the thickness of the poroelastic cylindrical shell and L is wavelength. Let
), C [= w/k] is phase velocity h is the thickness of the poroelastic cylindrical shell and L is wavelength. Let
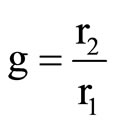 , so that
, so that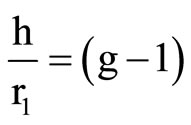 . (41)
. (41)
6. Results and Discussions
Two types of poroelastic materials are considered to carry out the computational work, one is sandstone saturated with kerosene, say Material-I (Fatt, [15]), the other one is sandstone saturated with water, Material-II (Yew and Jogi, [16]), whose non-dimensional physical parameters are given in Table 1.
For a given poroelastic material, frequency Equations (24) and (26), when non-dimensionalized using Equations (40) and (41), constitute a relation between nondimensional phase velocity x and ratio of thickness to wavelength d (= h/L) for fixed values of g. Different values of g, viz., 1.034, 3 and infinity are taken for numerical computation. These values of g represent thin poroelastic cylindrical shell, thick poroelastic cylindrical shell and poroelastic solid cylinder respectively. The values of d lie in [0, 1]. Non-dimensional phase velocity x is determined for different values of d and for fixed values of g, each for a pervious and an impervious surface. For poroelastic cylindrical shells immersed in an acoustic medium, the values of m, m1, t and t1 are taken as m = m1 = 1.5 and t = t1 = 0.4. To compute the frequencies of radial vibrations of poroelastic cylindrical shells immersed in an acoustic medium, Equations (34) and (38) are non-dimensionalized using Equations (40) and (41). Equations (34) and (38) constitute the relation between non-dimensional frequency W and ratio of thickness to inner radius h/r1. For broad spectrum of values of h/r1, frequency W is computed for the considered poroelastic materials-I and II. To compute the frequency of radial vibrations of poroelastic cylindrical shells immersed in an acoustic medium, the values of t, t1, m2, m3
are taken as t = t1 = 0.4, m2 = m3 = 1.5. The non-dimensional form of Equations (24), (26), (34), (38) are solved numerically to compute either the phase velocity or the frequency, following the analysis of Gazis [1]. The counterpart of frequency Equation (34) was not solved numerically for elastic medium by Chandra et al. [3] while the author solved these equations for poroelastic medium in a different paper.
The phase velocity of axially symmetric vibrations of poroelastic cylindrical shells immersed in an acoustic medium is presented in Figures 1-3 for materialI and II each for a pervious and an impervious surface. Figure 1 shows the phase velocity for materials-I and II in case of pervious and impervious surfaces. From Figure 1 it is clear that the phase velocity for a pervious surface is higher than that of an impervious surface in 0 £ d £ 0.5
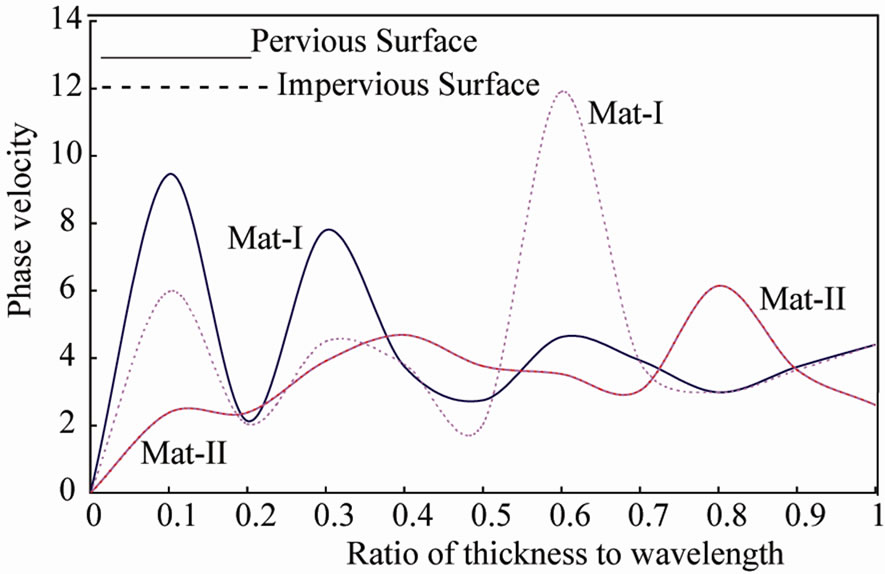
Figure 1. Phase velocity as a function of wavelength (Mat-I, Mat-II, Thin-Shell) axially symmetric vibrations of poroelastic cylindrical shells immersed in an acoustic medium.
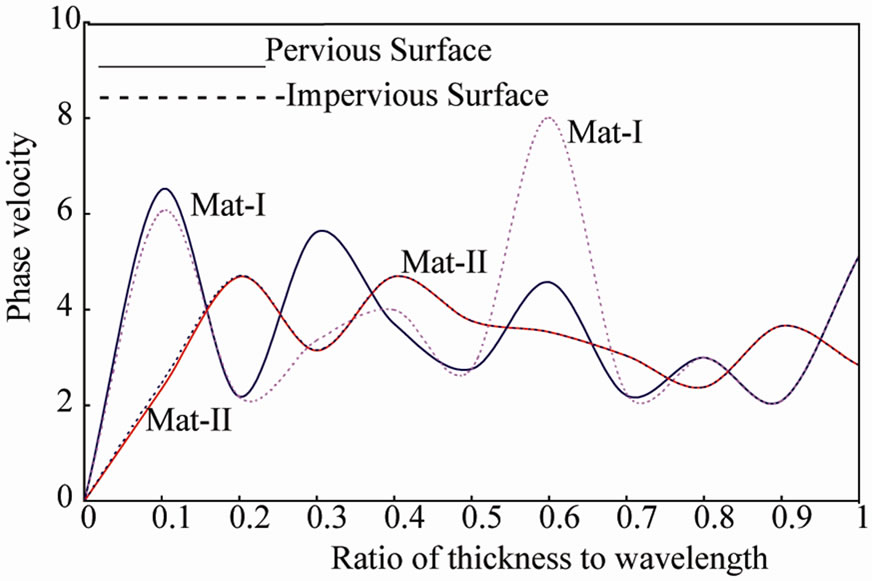
Figure 2. Phase velocity as a function of wavelength (Mat-I, Mat-II, Thick-Shell) axially symmetric vibrations of poroelastic cylindrical shells immersed in an acoustic medium.

Table 1. Material Parameters.
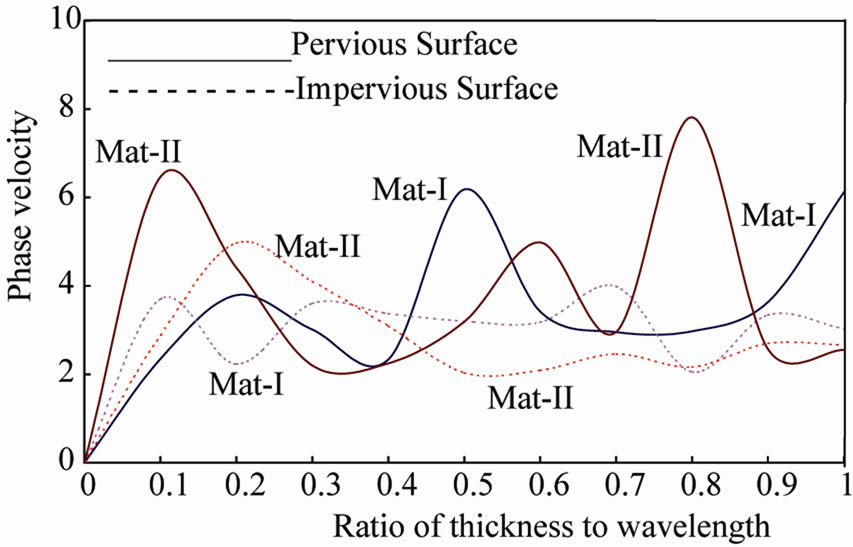
Figure 3. Phase velocity as a function of wavelength (Mat-I, Mat-II, Solid cylinder) axially symmetric vibrations of poroelastic solid cylinders immersed in an acoustic medium.
for material-I while beyond d = 0.5 it is less than or equal to the phase velocity of an impervious surface. The phase velocity of pervious and impervious surfaces is almost is same in case of material-II. The phase velocity for material-I, in general, is higher than that of material-II both for pervious and impervious surfaces. Thus it can be inferred that presence of mass-coupling parameter increases the phase velocity for thin poroelastic cylindrical shells immersed in an acoustic medium.
Figure 2 shows the phase velocity of thick poroelastic cylindrical shells immersed in an acoustic medium in case of materials-I and II each for a pervious and an impervious surface. It is seen from Figure 2 that the phase velocity of a pervious surface in case of material-I is almost same to that of an impervious surface in 0 ≤ d ≤ 0.2 and 0.7 ≤ d ≤ 1. In 0.2 ≤ d ≤ 0.5 the phase velocity of a pervious surface is higher than that of an impervious surface while in 0.5 £ d £ 0.7 it is less than that of an impervious surface. Again as in case of a thin poroelastic cylindrical shell, the phase velocity is same for pervious and impervious surfaces for thick poroelastic cylindrical shell. In general, the phase velocity for thick poroelastic cylindrical shell is higher in case of material-I than that of material-II. The phase velocity decreased with the increase of thickness for a pervious surface in case of material-I. In case of an impervious surface, in general, the phase velocity increases with the increase of thickness. Increase of thickness has no significant effect on phase velocity in case of material-II for pervious and impervious surfaces.
Figure 3 shows the phase velocity of poroelastic solid cylinders immersed in an acoustic medium each for a pervious and an impervious surface in case of materials-I and II. From Figure 3 it is clear that the phase velocity of pervious and impervious surfaces vary in a staggered way for material-I. In case of material-II, the phase velocity of a pervious surface, in general, is higher than that of an impervious surface unlike in case of poroelastic thin and thick cylindrical shells. Therefore it is inferred that the absence of mass-coupling parameter increases the phase velocity of a pervious surface of a poroelastic solid cylinder. Also the presence of mass-coupling parameter increases the phase velocity of an impervious surface of the poroelastic solid cylinder. In general, the phase velocity is less in poroelastic solid cylinder than that of either a thin shell or a thick shell both for pervious and impervious surfaces and for both the considered materials.
7. Concluding Remarks
The study of axially symmetric vibrations of poroelastic cylindrical shells immersed in an acoustic medium has lead to following conclusions:
1) Radial vibrations and axially symmetric shear vibrations are uncoupled when the wavenumber is zero.
2) The frequency equation of axially symmetric shear vibrations is independent of nature of surface and presence of fluid within and around the poroelastic cylindrical shell.
3) The phase velocity is same for pervious and impervious surfaces in case of material-II each for thin and thick poroelastic cylindrical shell.
4) In general, the phase velocity is higher for material-I than that of material-II each for a pervious and an impervious surface.
5) The frequency of radial vibrations of poroelastic cylindrical shell immersed in an acoustic medium for a pervious surface is higher than that of an impervious surface in case of material-I.
6) The frequency of an impervious surface is higher than that of a pervious surface in case of material-II.
8. Acknowledgements
The author is thankful to the Editor-in-Chief, the reviewers, and particularly the Editorial Assistant Mr. Judy Liu, for their suggestions and cooperation in improving the quality of this paper.
REFERENCES
- D. C. Gazis, “Three Dimensional Investigation of the Propagation of Waves in Hollow Circular Cylinders,” Journal of the Acoustical Society of America, Vol. 31, 1959, pp. 568-587. doi:10.1121/1.1907753
- L. Bjorno and R. Kumar, “Fluid Influenced Stress Wave Dispersion in Submerged Rods,” Acustica, Vol. 27, 1972, pp. 329-334.
- J. Chandra, R. Kumar and Y. K. Mehta, “Dispersion of Axially Symmetric Waves in Cylindrical Shells Immersed in an Acoustic Medium,” Acustica, Vol. 35, 1976, pp. 1-10.
- M. A. Biot, “Theory of Propagation of Elastic Waves in Fluid Saturated Porous Solid,” Journal of the Acoustical Society of America, Vol. 28, No. 2, 1956, pp. 168-178. doi:10.1121/1.1908239
- M. Tajuddin and K. S. Sarma, “Torsional Vibrations of Poroelastic Cylinders,” Journal of Applied Mechanics, Vol. 47, 1980, pp. 214-216.
- C. J. Wisse, D. M. J. Smeulders, M. E. H. van Dongen and G. Chao, “Guided Wave Modes in Porous Cylinders: Experimental Results,” Journal of the Acoustical Society of America, Vol. 112, No. 3, 2002, pp. 890-895. doi:10.1121/1.1497621
- C. J. Wisse, D. M. J. Smeulders, G. Chao and M. E. H. van Dongen, “Guided Wave Modes in Porous Cylinders: Theory,” Journal of the Acoustical Society of America, Vol. 122, No. 4, 2007, pp. 2049-2056. doi:10.1121/1.2767418
- G. Chao, D. M. J. Smeulders and M. E. H. van Dongen, “Shock-Induced Borehole Waves in Porous Formations: Theory and Experiments,” Journal of the Acoustical Society of America, Vol. 116, No. 2, 2004, pp. 693-702. doi:10.1121/1.1765197
- A. K. Vashishth and P. Khurana, “Wave Propagation along a Cylindrical Borehole in an Anistropic Poroelastic Solid,” Geophysical Journal International, Vol. 161, No. 3, 2005, pp. 295-302. doi:10.1111/j.1365-246X.2005.02540.x
- H. Farhang, E. Esmaeil, N. S. Anthony and A. Mirnezami, “Wave Propagation in Transversely Isotropic Cylinders,” International Journal of Solids and Structures, Vol. 44. No. 16, 2007, pp. 5236-5246. doi:10.1016/j.ijsolstr.2006.12.029
- M. Tajuddin and S. Ahmed Shah, “Circumferential Waves of Infinite Hollow Poroelastic Cylinders,” Journal of Applied Mechanics, Vol. 73, No. 4, 2006, pp. 705-708. doi:10.1115/1.2164513
- M. Tajuddin and S. Ahmed Shah, “On Torsional Vibrations of Infinite Hollow Poroelastic Cylinder,” Journal of Mechanics of Materials and Structures, Vol. 2, No. 1, 2007, pp. 189-200. doi:10.2140/jomms.2007.2.189
- S. Ahmed Shah, “Axially Symmetric Vibrations of Fluid Filled Poroelastic Circular Cylindrical Shells,” Journal of Sound and Vibration, Vol. 318, No. 1-2, 2008, pp. 389- 405. doi:10.1016/j.jsv.2008.04.012
- S. Ahmed Shah and M. Tajuddin, “On Axially Symmetric Vibrations Fluid Filled Poroelastic Spherical Shells,” Open Journal of Acoustics, Vol. 1, No. 2, 2011, pp. 15- 26. doi:10.4236/oja.2011.12003
- I. Fatt, “The Biot-Willis Elastic Coefficients for a Sandstone,” Journal of Applied Mechanics, Vol. 26, 1959, pp. 296-297.
- C. H. Yew and P. N. Jogi, “Study of Wave Motions in Fluid-Saturated Porous Rocks,” Journal of the Acoustical Society of America, Vol. 60, 1976, pp. 2-8. doi:10.1121/1.381045

