World Journal of Engineering and Technology
Vol.03 No.04(2015), Article ID:60978,10 pages
10.4236/wjet.2015.34019
Post-Buckling Behavior of Laminated Composite Cylindrical Shells Subjected to Axial, Bending and Torsion Loads
Yengula Venkata Narayana1, Jagadish Babu Gunda2*, Ravinder Reddy Pinninti3, Markandeya Ravvala4
1Department of Mechanical Engineering, Sreenidhi Institute of Science and Technology, Hyderabad, India
2Advanced Systems Laboratory, Kanchan Bagh, Hyderabad, India
3Department of Mechanical Engineering, Chaitanya Bharathi Institute of Science and Technology, Hyderabad, India
4Department of Metallurgical Engineering JNTUH, Hyderabad, India

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 8 August 2015; accepted 7 November 2015; published 10 November 2015

ABSTRACT
In present work, post-buckling behavior of imperfect (of eigen form) laminated composite cylindrical shells with different L/D and R/t ratios subjected to axial, bending and torsion loads has been investigated by using an equilibrium path approach in the finite element analysis. The Newton-Raphson approach as well as the arc-length approach is used to ensure the correctness of the equilibrium paths up to the limit point load. Post-buckling behavior of imperfect cylindrical shells with different L/D and R/t ratios of interest is obtained and the theoretical knock-down factors are reported for the considered cylindrical shells.
Keywords:
Post-Buckling, Cylindrical Shells, Eigen Imperfection Shapes, Axial Compressive Load, Bending Load, Torsion Load, Arc-Length Method, Knock-Down Factor

1. Introduction
Cylindrical shells are very often used as primary load carrying structural members in aerospace, civil, mechanical and nuclear engineering fields and these structural elements are very often subjected to multiple states of loading simultaneously such as the combination of axial, bending and torsion loads. The mechanical behavior of the above structural elements is extremely sensitive to the presence of geometric imperfections and the modeling of these geometric imperfections plays a pivotal role in accurately understanding the mechanical behavior by means of either an analytical or finite element analysis approaches. The complex behavior of these imperfect composite cylindrical shells subjected to axial compressive [1] -[3] , bending [4] [5] and torsion [6] -[13] loads has been investigated by many researchers across the world and the complete understanding of the mechanical behavior of these cylindrical shells subjected to different combinations of these fundamental loads is still an active area of current research.
Recently authors have carried out an extensive literature review in References [1] -[3] on analysis of imperfect (eigen form) cylindrical shells made up of isotropic as well as laminated composite cylindrical shells subjected to axial compressive load, and much emphasis is not made here on the same in order to abridge the proposed paper. The work done by the authors’ in Ref. [2] on analysis of cylindrical shells is only restricted to axial compressive load only and is a major source of motivation to pursue the proposed research work with an endeavor to understand the post-buckling behavior of cylindrical shells with other forms of fundamental loading.
Karyadi [4] investigated the influence of length variation on the linear buckling behavior of isotropic cylindrical shells subjected to pure bending and the results of this study show that the maximum critical bending stress is essentially equal to the critical uniform axial compressive stress. Although the aforementioned statement by Karyadi [4] is concluded quantitatively by performing a linear buckling analysis only, however the concluding statement needs a better explanation from the nonlinear phenomenon as this approach can effectively capture the influence of imperfections on post-buckling behavior of imperfect cylindrical shells.
Yamaki [6] [7] and Wang et al. [8] have carried out many experiments on the torsional buckling of elastic cylindrical shells and described that the buckling wave doesn’t occupy the complete length of the long cylindrical shell in contrast to the short cylindrical shell. Wang et al. [8] also compared their experimental torsional buckling results with that of Yamaki [6] results and furthermore they concluded that the influence of axial and circumferential boundary condition was less important in the torsional buckling analysis of elastic cylindrical shells. Kim et al. [10] developed a 3D elastic solution to the buckling of orthotropic cylindrical shells subjected to torsional loads and the accuracy of the existing shell theories had been assessed with that of 3D elastic solution. Park et al. [11] investigated the torsional buckling loads (limit point loads) of various composite cylindrical shells by using the geometrically nonlinear finite element analysis approach. Bisagni et al. [12] have carried out an experimental study on post-buckling behavior of CFRP cylindrical shells subjected to axial and torsion loads which are applied separately as well as in combination to arrive at various interaction curves.
The exhaustive study on post-buckling behavior of laminated composite cylindrical shells subjected to general fundamental load cases such as axial, bending and torsion loads with different L/D and R/t ratios is meagerly seen in the available open literature. The proposed piece of work makes a modest attempt to bridge this gap with an endeavor to understand the post-buckling behavior of the laminated composite cylindrical shells subjected to these fundamental loads.
2. Finite Element Formulation
The finite element discretization process for geometrically non-linear analysis yields a set of simultaneous equations:
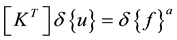 (1)
(1)
where 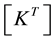 is the tangent stiffness matrix,
is the tangent stiffness matrix, 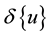 is the incremental nodal displacement vector and
is the incremental nodal displacement vector and 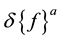 is the incremental nodal force vector. For determining the buckling load, the equation can be simplified by taking small deformation and we can omit the nonlinear terms which are functions of nodal displacements in the tangent stiffness matrix. The following expression [14] gives the tangent stiffness matrix after linearization
is the incremental nodal force vector. For determining the buckling load, the equation can be simplified by taking small deformation and we can omit the nonlinear terms which are functions of nodal displacements in the tangent stiffness matrix. The following expression [14] gives the tangent stiffness matrix after linearization
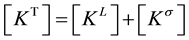 (2)
(2)
where 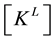 is a linear stiffness matrix and
is a linear stiffness matrix and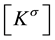 , a stress stiffness matrix. If a stress stiffness matrix
, a stress stiffness matrix. If a stress stiffness matrix 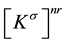 is generated according to a reference load
is generated according to a reference load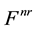 , for another load level
, for another load level 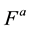 with
with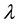 , a scalar multiplier, we have
, a scalar multiplier, we have
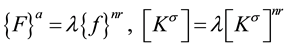 (3)
(3)
When buckling occurs, the external loads do not change, i.e., 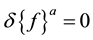 Then the bifurcation solution for the linearized buckling problem may be determined from the following eigenvalue equation:
Then the bifurcation solution for the linearized buckling problem may be determined from the following eigenvalue equation:
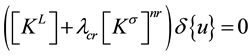 (4)
(4)
where 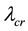 is an eigenvalue and
is an eigenvalue and 






3. Post-Buckling Analysis
Nonlinear analysis of a geometrically perfect or imperfect cylindrical shell using Newton-Raphson approach generally involves the determination of the equilibrium path up to the limit point load and beyond which the slope of the load-deflection curve (or equilibrium path) ceases to be positive. Post-buckling analysis by means of an arc-length approach generally involves the determination of the full equilibrium path which also includes tracing of the unstable solution of the equilibrium path. Salient steps involved in arriving at the post-buckling behavior of imperfect cylindrical shells are briefly summarized below:
Steps Followed in Post-Buckling Analysis
1) The linear buckled mode shape has been chosen as the basis of initial imperfection. Magnitude of initial
Figure 1. (a) Axial compressive load; (b) Bending moment; (c) Torsion load.
imperfection is referred with reference to the thickness (t) parameter of the cylindrical shell. It must be noted that the shape of imperfection can be given in the form of linear combination of buckled mode shapes or random imperfection or experimentally measured imperfection shape.
2) After applying initial geometric imperfection, a nonlinear analysis has been performed to trace the equilibrium path of interest.
3) Nonlinear analysis involves the application of either Newton-Raphson approach or an arc-length approach to solve Equation (1).
4) Load-deflection curve obtained from the Newton-Raphson approach represents the primary equilibrium path where as the load-deflection curve traced in an arc-length approach includes the primary (stable) as well as secondary (unstable) equilibrium paths. All the proposed results use an arc-length method for post-buckling analysis results unless otherwise it is explicitly mentioned.
4. Results & Discussion
In present work, post-buckling behavior of the laminated composite cylindrical shells subjected to axial, bending and torsion loads has been investigated by using the post-buckling analysis.
4.1. Axial Compressive and Bending Load
Throughout this study, the cylindrical shell is assumed to be laminated composite cylindrical shell made up of E-glass/polyester resin and the material properties are directly taken from Ref. [15] which are indicated in Table 1. The radius of the cylindrical shell is considered as 150 mm. The length and thickness of the cylindrical shell in general varies in accordance with the L/D and R/t ratios as specified wherever applicable. One end of the cylinder is simply supported, whereas the axial load or bending moment is applied on the other end of the cylindrical shell. Eigen form of imperfection shapes are considered on the basis of fundamental buckled mode shapes with different imperfection magnitudes of interest. Figure 2 and Figure 3 show the comparison of the numeri-
Figure 2. Comparison of limit point loads of an axially compressed composite cylindrical shell.
Table 1. Material properties [15] of the E-glass/polyester resin.
cal results obtained from the Newton Raphson approach as well as the arc-length approach for a typical imperfection magnitude (ξ = w*/t, where w* is the maximum imperfection amplitude and t is the thickness of the cylindrical shell) of laminated composite cylindrical shell subjected to axial compressive and bending load respectively. In general, it is observed that these two approaches have shown good agreement in predicting the primary equilibrium path as well as in predicting the limit point load of the considered composite cylindrical shells which in turn poses as a benchmark validation for all the results discussed in this paper. For the sake of better clarity to the reader, only post-buckling analysis results obtained from the arc-length approach are only discussed subsequently in the paper.
Figure 4 shows that influence of different eigen imperfection magnitudes on post-buckling behavior of the laminated composite cylindrical shells subjected to axial compressive load which indicates that the limit point load decreases with increase in imperfection magnitudes. Figure 5 shows the parametric influence of L/D ratio on variation of limit point loads which conveys that the cylinders with higher L/D values are less imperfection sensitive relative to the lower L/D values. Table 2 summarizes the eigen imperfection sensitivity (or knock-down factors) of various cylindrical shells subjected to axial compressive load with different L/D and R/t ratios which provides an overview on variation of the limit point load with different eigen imperfection magnitudes of interest. Furthermore, the influence of bending load on post-buckling behavior is discussed in Figure 6 with different
Figure 3. Comparison of limit point loads of cylindrical shell subjected to bending load.
Figure 4. Effect of eigen imperfection sensitivity on cylindrical shell subjected to axial load.
Figure 5. Influence of L/D ratio on cylindrical shell subjected to axial load.
Figure 6. Effect of eigen imperfection sensitivity on cylindrical shell subjected to bending load.
Table 2. Knock-down factors of various cylindrical shells subjected to axial compressive load (ply sequence (−45/−45/+45)s).
eigen imperfection magnitudes and in Figure 7 with different L/D ratio with an objective of understanding the influence of loading nature. Table 3 summarizes the knock-down factors of various cylindrical shells subjected to bending load for various eigen imperfection magnitudes. A close comparison of Table 2 and Table 3 indicates the sensitivity envelop of the limit point loads of various cylindrical shells subjected to axial and bending loads which infers that the limit points are more sensitive to the bending load rather than an axial load as the L/D ratio increases with eigen form of imperfection shape.
4.2. Torsion Load
Numerical results (Linear or Critical torsional buckling loads) obtained from the present work are first validated in Table 4, Table 5 and Table 6 with the various available literature values for the cylindrical shells subjected to torsion load which indicates the consistency and adequacy of the present numerical results. Subsequently, the post-buckling analysis has been carried out to the previously considered composite cylindrical shells (considered properties are shown in Table 7) in order to understand the influence of eigen imperfection sensitivity as well as the influence of other geometric parameters such as L/D and R/t ratios. Figure 8 shows the influence of different eigen imperfection magnitudes on post-buckling behavior of the composite cylindrical shells subjected to torsional load which indicates the normalized load sustaining behavior of the cylindrical shell subjected to torsion. Figure 9 shows the parametric influence of L/D ratio on the normalized load sustaining behavior of the cylin-
Figure 7. Influence of L/D ratio on cylindrical shells subjected to bending load.
Table 3. Knock-down factors of various cylindrical shells subjected to bending load (ply sequence (−45/−45/+45)s).
Figure 8. Effect of eigen imperfection sensitivity on cylindrical shells subjected to torsion.
Figure 9. Influence of L/D ratio on cylindrical shells subjected to torsion.
Table 4. Comparison of linear torsional buckling loads of an isotropic cylindrical shell with the other available literature values.
Table 5. Comparison of linear torsional buckling loads with R/t = 100 (ply sequence [0/90/0]S).
drical shells. Table 8 summarizes the eigen imperfection sensitivity of various cylindrical shells subjected to torsion load with different L/D and R/t ratios which conveys the variation of the limit point loads with different imperfection magnitudes of interest. Finally, Table 9 shows the qualitative comparison of the knock-down factors of various cylindrical shells subjected to axial, bending and torsion loads which indicates that in general cylindrical shells are relatively less imperfection sensitive in torsion loading as compared to axial compressive and bending loads.
In all Table 2, Table 3, Table 8 and Table 9, Z is the Batdorf parameter (considered as a measure of Geometry parameter) and its value is presented to understand its qualitative influence on variation of knock-down factors.
Table 6. Comparison of linear torsional buckling loads with R/t = 100 (ply sequence [30/30/−60]S).
Table 7. Mechanical properties [11] of composite cylindrical shell.
Table 8. Knock-down factors of various cylindrical shells subjected to torsion (ply sequence (−45/−45/+45)s).
Table 9. Comparison of knock-down factors of various cylindrical shells subjected to axial, bending and torsion load (ply sequence (−45/−45/+45)s).
4.3. Conclusion
Post-buckling behavior of laminated imperfect (of eigen form) composite cylindrical shells subjected to different fundamental loads is investigated by using an equilibrium path approach. Numerical results obtained from the proposed study are validated with the available literature values wherever they are found applicable, apart from providing comprehensive post-buckling analysis results subjected to different fundamental loads. The sensitivity of the limit point loads (or knock-down factors) for various cylindrical shells with different fundamental loading conditions is clearly discussed.
5. Future Works
Proposed study finds an immediate application in fundamental understanding of the mode jumping phenomenon which is commonly associated with the behavior of cylindrical shells subjected to different combination of loads as well as material properties. The confidence gained on this study can also be extended to investigate the influence of either random imperfection shapes (or) actually measured imperfection shapes. The detailed outcome of the above studies will be reported in future works planned by the authors’.
Cite this paper
Yengula VenkataNarayana,Jagadish BabuGunda,Ravinder ReddyPinninti,MarkandeyaRavvala, (2015) Post-Buckling Behavior of Laminated Composite Cylindrical Shells Subjected to Axial, Bending and Torsion Loads. World Journal of Engineering and Technology,03,185-194. doi: 10.4236/wjet.2015.34019
References
- 1. Kobayashi, T., Mihara, Y. and Fuji, F. (2012) Path-Tracing Analysis for Post-Buckling Process of Elastic Cylindrical Shells under Axial Compression. Thin Walled Structure, 61, 180-187.
http://dx.doi.org/10.1016/j.tws.2012.05.018 - 2. Yenugula, V.N., Gunda, J.B., Reddy, P.R. and Markandeya, R. (2013) Non-Linear Buckling and Post-Buckling Analysis of Cylindrical Shells Subjected to Axial Compressive Loads: A Study on Imperfection Sensitivity. Nonlinear Engineering, 2, 83-95.
- 3. Yenugula, V.N., Gunda, J.B., Pinninti, R.R. and Ravvala, M. (2013) Nonlinear Buckling and Post-Buckling Analysis of Laminated Composite Cylindrical Shells Subjected to Axial and Pressure Loads. The Ninth International Conference on Vibration Engineering and Technology of Machinery (VETOMAC-IX), VET2013214, China, 20-23 August 2013.
- 4. Karyadi, E. (1991) The Effect of Length Variation on the Stability of Circular Cylindrical Shells under Pure Bending. TU-Delft, Report LR-669.
- 5. Tafreshi, A. and Bailey, C.G. (2007) Instability of Imperfect Composite Cylindrical Shells under Combined Loading. Composite Structures, 80, 49-64.
http://dx.doi.org/10.1016/j.compstruct.2006.02.031 - 6. Yamaki, N. (1976) Experiments on the Post-Buckling Behavior of Circular Cylindrical Shells under Torsion Buckling of Structures. Edited by Buduansky, 312-330.
- 7. Yamaki, N. (1984) Elastic Stability of Circular Cylindrical Shells. North-Holland Press, Amsterdam.
- 8. Wang, D.-Y., Ma, H.-W. and Yang, O.-T. (1992) Studies on the Torsion Buckling of Elastic Cylindrical Shells. Applied Mathematics and Mechanics, English Edition, 13, 211-215.
- 9. Kruzelecki, J. and Trybula, D. (2007) Optimal Stabilization of Post-Buckling Path for Cylindrical Shells under Torsion. Proceedings of Seventh World Congress on Structural and Multidisciplinary Optimization, ISSMO, Seoul, 21-25 May 2007, 1523-1533.
- 10. Kim, Y.S., Kardomateas, G.A. and Zureick, A. (1999) Buckling of Thick Orthotropic Cylindrical Shells under Torsion. Journal of Applied Mechanics-Transactions of the ASME, 66, 41-50.
http://dx.doi.org/10.1115/1.2789167 - 11. Park, H.C., Cho, C.M. and Choi, Y.H. (2001) Torsional Buckling Analysis of Composite Cylinders. AIAA Journal, 39, 951-955.
http://dx.doi.org/10.2514/2.1400 - 12. Bisagni, C. and Cordisco, P. (2003) An Experimental Investigation into the Buckling and Post-Buckling of CFRP Shells under Combined Axial and Torsion Loading, Experimental Buckling of Thin Composite Cylinders in Compression. Composite Structures, 60, 391-402.
http://dx.doi.org/10.1016/S0263-8223(03)00024-2 - 13. Daniel, J.K. (2010) Optimal Axial Tension and Internal Pressure Stabilizing Post-Buckling Path for Cylindrical Shells under Torsion. Journal of Theoretical and Applied Mechanics, 48, 645-658.
- 14. ANSYS, Inc. Theory Reference Manual.
- 15. Spagnoli, A., Elghazouli, A.Y. and Chrysanthopoulos, M.K. (2001) Numerical Simulation of Glass-Reinforced Plastic Cylinders under Axial Compression. Marine Structures, 14, 353-374.
http://dx.doi.org/10.1016/S0951-8339(00)00008-3
NOTES
*Corresponding author.












