International Journal of Analytical Mass Spectrometry and Chromatography
Vol.2 No.2(2014), Article
ID:47524,12
pages
DOI:10.4236/ijamsc.2014.22006
Solubility Modeling of N-CBZ Derivatised Amino Acids in Supercritical Carbon Dioxide
N. Vedaraman1, Pravin Gadkari2,3, Balaraman Manohar2,3, K. V. Sandhya1, Gerd Brunner4, K. Udaya Sankar2*
1CSIR-Central Leather Research Institute, Chennai, India
2Food Engineering, CSIR—Central Food Technological Research Institute, Mysore, India
3Academy of Scientific and Innovative Research, CSIR-CFTRI, Mysore, India
4VT-2, TUHH, Hamburg, Germany
Email: *udayaskadimi@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 April 2014; revised 27 May 2014; accepted 19 June 2014
ABSTRACT
The experimental solubility of CBZ (Carbobenzoxy) derivatized amino acids namely N-CBZ valine, N-CBZ proline, N-CBZ aspartic acid in supercritical carbon dioxide were correlated by Soave-Redlich-Kwong Equation state based on fugacity determination and group contribution method using extrapolated critical parameters and mixing rules and other two different empirical models proposed by Yu (1994) and Gordillo-coworkers (1999). The SRK EOS prediction showed very high deviation of % AARD of 9% - 59%. The Yu model had three derivatized amino acids with average absolute deviation from 2.04, 8.17, 10.96, while the Gordillo model had 0.245, 1.067 and 1.144 for CBZ-valine, CBZ-proline and CBZ-aspartic acid successively. The correlated values had better fit with Gordillo model. The predictive capability and applicability for these amino acid derivatives for both the models demonstrated with correlation coefficient around 0.99 for all the experimental solubility observed.
Keywords:Derivatized Amino Acids, Soave-Redlich-Kwong (SRK), Yu Model, Gordillo Model

1. Introduction
Growing concern on the adverse environmental impact in industrial processing, stringent legislation on the solvent residues in food extracts or products, growing demand by the consumers as well as the processors for safe and products, new modes of production processes are intensely pursued in the industry for the past two decades. One of the major processing technologies that are increasingly applied in industry are high pressure technology based on the use of supercritical CO2 processes for extraction, sorption process, chromatography, drying, nucleation, membrane separation, encapsulation, impregnation, biochemical reactions and chemical reactions [1] - [3] . Supercritical fluids came into the fore front in view of their properties that help favorable mass transfer properties, such as high diffusivities and compressibility’s gas like tending to liquid, liquid like densities and no surface tension, variable solvent power based on tuning the pressure and temperature that help in selective separation due to variable solute solubility [4] [5] . Supercritical carbon dioxide is the solvent of choice in view of the fact the critical temperature (31.2˚C) is near ambient, non-toxic, non-inflammable, inexpensive and used soft drinks for carbonation as GRAS substance [1] .
In chemical process whether it is a separation or reaction, the experimental solubility of the solute in the reaction media, say carbon dioxide (SCF solvent) is very essential. Although innumerable studies on solubility had taken place [6] , still there is a dearth for solubility data on compounds in supercritical fluids. Wherever there is a solubility data to extrapolate to the different conditions, it is necessary model the solubility data based on thermodynamic equation of state that needs the critical properties of the solutes, acentric factors, vapour pressure data, density data of solute in gas, liquid and solid phases, and density of mixtures. For most of the biological activity compounds such data is not available and need to extrapolated either by group contribution methods. Sometimes, it is better follow empirical models to fit the experimental data for extrapolation in waste and process engineering [7] .
Slaughter house and tannery wastes such as poultry feathers, animal flesh, hair, horn, and hoof are major source of environmental pollution and receiving much attention for researchers. These protein waste materials can be subjected to acid or alkali hydrolysis and extract to obtain different aminoacids in purer form. But the separation of amino acids using supercritical fluids hindered due to their poor solubility due to their polar nature. The amino acids are derivatised to carbozoxybenzene to enhance their solubility in supercritical carbon dioxide [8] . By derivatisation of the amino acids, where the both the polar groups such as amino and carboxylic acid groups are blocked, the solubility is further enhanced for ease of separation and purification in supercritical carbon dioxide.
There are several empirical models projected in past decade such as Mendez-Santiago-Teja, Modified Mendez-Santiago-Teja, Bartle, Yu, Charstil, and Gordillo model, which gives good promise with experimental data over wide range of temperature and pressure [9] -[13] . The easiest way of correlating solubility data is empirical fit where the relationship between thermodynamic property such as pressure and density can be fitted and presented linearly. Basically there are three types of models namely solubility parameter model, density and chemical association semi-empirical models [7] . Some commonly used equation of states that help the modeling of solubility parameter model are Soave-Redlich-Kwong equation of state, Peng-Robinson equation of state, and Lee-Kesler-Plocker equation of state. These equations of state are more complicated than empirical or semiempirical model, because it requires more efforts to figure out the unknown constants such as critical temperature, critical pressure, critical volume and acentric factors in the model. Also the solute properties are not available for complex structures such as some proteins and amino acids in which complicated computational prediction and group contribution methods are involved [14] .
The present study is aimed at correlation of the solubility of the N-CBZ amino acids carried out by Vedaraman et al. (2004) using 1) Soave Redlich-Kwong equation and empirical models developed by 2) Yu et al. (1994) and 3) Gordillo et al. (1999).
2. SRK EOS Based Correlation and Prediction of Solubility CBZ N-Amino Acids
Soave-Redlich-Kwong thermodynamic model for correlating the solubility of solutes at high pressures by appropriate corrections for volume of the gas and appropriate mixing rules. It involves the data on critical properties of both the solvent and the solute, determination of mixed parameters using appropriate mixing rules [15] .
The critical temperature (Tc) and the critical pressure (PC) of the CBZ-N-amino acids determined by Lyderson’s critical property group contribution increments based on chemical structure was used [16] .
 (2.1)
(2.1)
where TB = Normal Boiling temperature, q = TB/TC
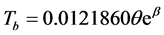
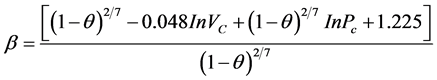 (2.2)
(2.2)
ΔTL = Group Contributions for temperature in Lydersen Equation (2.1);
Mw = molecular weight of the compound.
The following Equation (2.3) was used for predicting critical pressure based on group contribution methods.
Lydersen
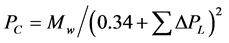 (2.3)
(2.3)
For calculatin the acentric factor, ω, Lee-Kesler Equation (2.4) was used
 (2.4)
(2.4)
The critical volume is extrapolate by Lydersen group contribution methods
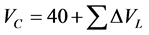 (2.5)
(2.5)
ΔVL = Group Contributions for volume in Lydersen Equation (2.5).
Generally measurements of boiling points are made at lower pressures for extremely high boiling compounds or for compounds that decompose (especially true for bio-active components such as bakuchiol) before they boil at atmospheric pressure [17] . Joback used the same approach to develop a method for normal boiling point as he used to develop a method for critical temperature. The resulting method is a function of structure only. The Joback’s equation for calculating the boiling point is shown below:
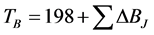 (2.6)
(2.6)
where ΔBJ = Group Contributions for boiling point.
The vapor pressure is the pressure exerted by a pure component at equilibrium at any temperature when both liquid and vapor phases exist and thus extends from a minimum at the triple point temperature to a maximum at the critical temperature, the critical pressure.
In the present study to calculate vapour pressures, the Equations (2.7) to (2.76) were adopted from studies of Edalat and Bozar-Jomehri [18] . The method is claimed to be accurately predicting vapor pressure of hydrocarbons, non-hydrocarbons and polar fluids using only Pc, Tc and ω, the acentric factor. The equation is described below:
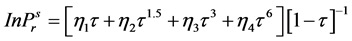 (2.7)
(2.7)
where,
 (2.71)
(2.71)
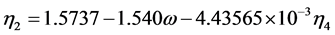 (2.72)
(2.72)
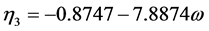 (2.73)
(2.73)
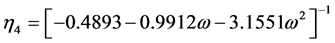 (2.74)
(2.74)
 (2.75)
(2.75)
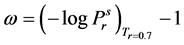 (2.76)
(2.76)
where 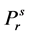 = reduced vapor pressure (Ps/Pc). η1, η2, η3, η4 = constants defined in Equations (2.71) to (2.76).
= reduced vapor pressure (Ps/Pc). η1, η2, η3, η4 = constants defined in Equations (2.71) to (2.76).
Equations of state are used to describe the thermodynamic states through the relationship of state parameters such as temperature, pressure, and volume. In SCFE processing, EOS describes the behavior of solute being dissolved in supercritical fluids. The solubility of a substance (component 2) in a supercritical fluid (component 1) can be obtained from fluid-solid phase equilibria. The subscripts 1 and 2 in the following derivations denote components CO2 and solute. At equilibrium, the fugacities of the components in the solid and gas phases are equal, i.e.
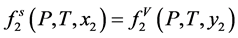 (2.8)
(2.8)
where  is the fugacity of solute in the solid phase;
is the fugacity of solute in the solid phase; 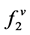 fugacity of solute in the gas phase; P is the pressure; T is the temperature; x and y are mole fractions.
fugacity of solute in the gas phase; P is the pressure; T is the temperature; x and y are mole fractions.
If the gas component 1 is assumed to be insoluble in solid phase (true in most of the cases), then
 (2.81)
(2.81)
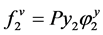 (2.82)
(2.82)
where, φ is the fugacity coefficient; V molar volume; R is the universal gas constant; superscripts s and sat denote solid and saturated conditions respectively.
From above equations, one can obtain:
 (2.83)
(2.83)
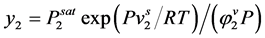 (2.84)
(2.84)
where, E is the enhancement factor which is the ratio of the solubility of the solute in super critical fluid to the solubility in an ideal gas. i.e. 
Large enhancement factors of the order of 105 to 107 are frequently observed due to small values of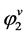 .
. .
. 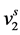 can be easily calculated from the density of component 2. Thus, to calculate E, one requires the value of
can be easily calculated from the density of component 2. Thus, to calculate E, one requires the value of . From well-known equation of state (EOS) available such as Peng-Robinson (PR) and Soave-Redlich-Kwong (SRK) models,
. From well-known equation of state (EOS) available such as Peng-Robinson (PR) and Soave-Redlich-Kwong (SRK) models, 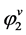 can be calculated.
can be calculated.
A general form of the SRK equation is:
Soave-Redlich-Kwong equation of state (SRK-EOS) is:
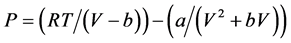 (2.9)
(2.9)
The above can also be written as:
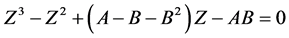 (2.91)
(2.91)
The above equation leads to:
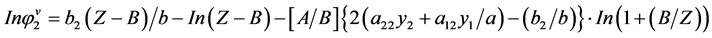 (2.92)
(2.92)
where
 (2.93)
(2.93)
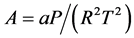 (2.94)
(2.94)
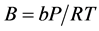 (2.95)
(2.95)
a = intermolecular attraction parameter;
b = covolume parameter.
3. Mixing Rules for SRK EOS
When the equation is extended to mixtures, the following mixing rule is employed:
 (2.96)
(2.96)
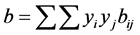 (2.97)
(2.97)
where aij and bij are calculated from combining rules:
 (2.98)
(2.98)
 (2.99)
(2.99)
where, kij and nij are the adjustable binary interaction parameters. The adjustable parameters are determined by regressing phase equilibrium data and assumed to be independent of temperature, pressure and composition. It may be noted that these parameters can take negative values and accordingly, the software program should be allowed to adjust these values suitably. Many authors have used single binary interaction parameter kij in their works. However, a second adjustable mixture parameter nij is also used in the present study, since nij can account for the large size disparity between a heavy non-volatile solute and a light SCF solvent [19] . For pure components, “a” and “b” parameters are calculated from critical constants Tc, Pc and acentric factor, ω depending on the type of EOS.
For SRK-EOS,
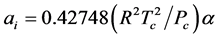 (3.00)
(3.00)
 (3.10)
(3.10)
 (3.11)
(3.11)
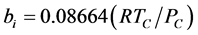 (3.12)
(3.12)
The computer program obtains the optimum kij and nij value by simple optimization technique which gives minimum average absolute relative deviation (AARD) between experimental and calculated values of solubility:
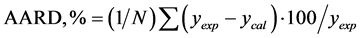 (3.2)
(3.2)
where N is the number of experiments, ycal and yexp are the calculated and experimental solubility of solute components respectively.
Experimental solubility is calculated from the slopes of the initial linear portion of extraction curve of total extract versus CO2 consumed [20] . When the extract is assumed as a single pseudo-component, the TC, PC, ω, Psat of the extract is considered to be sum of the property of the main components multiplied by mole fraction of main components.
The entire calculation procedure [21] described above can be summarized as below:
1) The critical values Tc, Pc and acentric factor for each component are estimated by group contribution methods.
2) Pure component parameters of the SRK-EOS are estimated.
3) kij and nij are assumed initial values. Then a and b for mixture are calculated based on mixing rules.
4) The cubic equation of state is solved for Z.
5)  is calculated.
is calculated.
6) y2 is calculated.
7) Steps 2 to 6 repeated for each pressure. AARD is then calculated. If AARD is not within tolerance limit set by the program, the procedure is repeated so that one obtains the optimal kij and nij parameters.
A program is written in Fortran 77 incorporating the above steps to calculate the solubility with minimum deviation.
4. Empirical Model Developed by Yu et al. [11]
Yu et al. developed an empirical model where the solubility as a function of pressure and temperature using quadratic equation. The solubility of methyl esters, ethyl esters, fatty acids, triglycerides, and fats and oils were studied over a range of temperature and pressures. The solubility data from the literature were correlated using the Peng-Robinson equation of state and mixing rules of van der Waals (VDW) and Panagiotopoulos and Reid. The triglyceride solubility in turn found to be in terms chain length, degree of unsaturation and function groups influence the solubility in supercritical carbon dioxide. An empirical equation in turn developed to fit better for large fatty acids, fatty acid esters and triglyceride molecules as a function of the pressure and temperature.
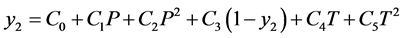 (4.1)
(4.1)
5. Empirical Model Developed by Gordillo and Coworkers [13]
Gordillo and coworkers developed logarithmic function of the solubility equation as function of temperature and pressure of the system for Pencillin G in supercritical carbon dioxide and they used a dynamic flow apparatus for the solubility measurement of Pencillin G at pressures from 100 to 350 bar and temperature 313.5 to 333.15 K [13] Physical and Critical properties of Pencillin G were extrapolated by group contribution methods using Fedor’s and Ambrose’s and correlated with EOS by Redlich-Kwong and Soave modified Redlich-Kwong with Lorent-Berthelot mixing rules. A second order empirical model to correlate solubility with temperature and pressure as logarithmic function, the same empirical model has been used in the correlation of solubility of the derivatized amino acids.
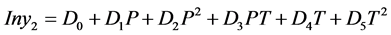 (5.1)
(5.1)
6. Results and Discussion
Table 1 provides the experimental solubility of N-CBZ amino acids in supercritical carbon dioxide as determined by Vedaraman et al. [8] . Compared to underivatised amino acids, the solubility of N-CBZ valine, proline and aspartic acid in supercritical carbon dioxide has showed increase, in the range of 10−4 mole fraction which is quite high. Table 2 provide the critical parameters of the carbon dioxide and the N-CBZ-Valine, Proline and Aspartic acid, the critical pressure is found to be less around 22 - 24.65, while the critical temperature as observed
Table 1 . Experimental solubility data of the N-CBZ derivatized amino acids in supercritical carbon dioxide (Vedaraman et al. 2004).
are high >900 K, while temperature of boiling 700 - 800 K as predicted by group contribution methods, while at these temperatures, these compounds undergo to vapour states. The acentric factors are high when compared to most of the normal compounds as they tend to be more polar. The Psat is very low and it is in the of order 10−12 moles, while solubility is observed of the order 10−5 moles, showing solubility enhancements of the order of 106 to 107 per mole of carbon dioxide is of several thousands. The soave modified Redlich-Kwong equation of state based prediction using the mixing rules correlated with % AARD 9% - 65%, while the CBZ-N-valine showed the highest % AARD, while the kij value are 0.44 to 0.46 (Table 3).
Table 4 provide the coefficients of the Equation (4.1) of the various parameters of correlated solubility of the derivatized CBZ-N-amino acids as predicted using the excel software (excel version 2010 MS Office 2010), the % AARD as calculated by the Equation (3.2) for CBZ-N-Valine is 2.04, while the regression statistical analysis showed the R square 0.989, standard error of 4.06E−05 and F significance is 5.57E−05, the p-values of the coefficient for all the parameters is less than 0.05 showing strong significance for all the coefficients except for PT(1-y) is higher showing less significance. In case of N-CBZ-proline, the % AARD is 8.17, while statistical analysis showed the R2 is 0.989, standard error 3.23E−05, and F significance 2.06E−06, the p-values of all the coefficients is less than 0.05 showing strong significance of fit for all the coefficients. For N-CBZ-Aspartic acid, the % AARD is 10.96, the R2 is 0.989, standard error 2.74E−05 and F significance 5.57E−05, the p-values of the coefficients is less than 0.05 showing strong statistical significance of fit. The Figure 1 shows the graphical fit of solubility with different pressures and temperatures for N-CBZ-valine, proline and aspartic acid.
Table 2. Critical Properties of carbon dioxide the derivatized amino acids obtained by group contribution methods based on Lyderson, volume properties by Vetere group contribution methods, accentric factor by Lee-Kesler equation.
Table 3. Parameters for SRK EOS for correlation of solubility of carbon dioxide and the derivatized amino acids at different temperatures.
Table 4. The coefficients of the equation Yu et al. 1994 model for the correlation of the solubility of the derivatized amino acids.

Figure 1. Model plot obtained using Yu model showing effect of pressures and temperatures on solubility of amino acids (a) N-CBZ valine; (b) N-CBZ-proline and (c) N-CBZ-aspartic acid in supercritical CO2.
The Gordillo model based coefficients for the Equation (5.1) of the various parameters of correlated solubilities of the dervatized amino acids as predicted using excel software, is provided in Table 5, the % AARD as calculated by the Equation (3.2) for N-CBZ-valine is 0.245, while the regression statistical analysis showed R square 0.997, standard error 0.0369 and F significance 4.14E−10, the p-values are less than 0.05 showing strong significance of the fit. For N-CBZ-proline the %AARD as calculated by the Equation (3.2) is 1.067, while the regression statistical analysis showed R square 0.967, standard error 0.0369 and F significance 4.13E−5, the pvalues are less than 0.05 showing strong significance of the fit. For N-CBZ-aspartic acid the %AARD as calculated by the Equation (3.2) is 1.144, while the regression statistical analysis showed R square 0.982, standard error 0.1705 and F significance 0.000266, the p-values are less than 0.05 showing strong significance of the fit. Figure 2 provide the graphical values of y for different temperatures and pressures for N-CBZ-valine, proline and aspartic acid. Table 6 provides values for correlation of the solubility of said compounds by both the Yu and Gordillo models. It is clearly observed that out of the models the empirical model Gordillo (2004) is observed for a better fit when compared to SRK model of correlation of solubility of the CBZ-N-amino acids.
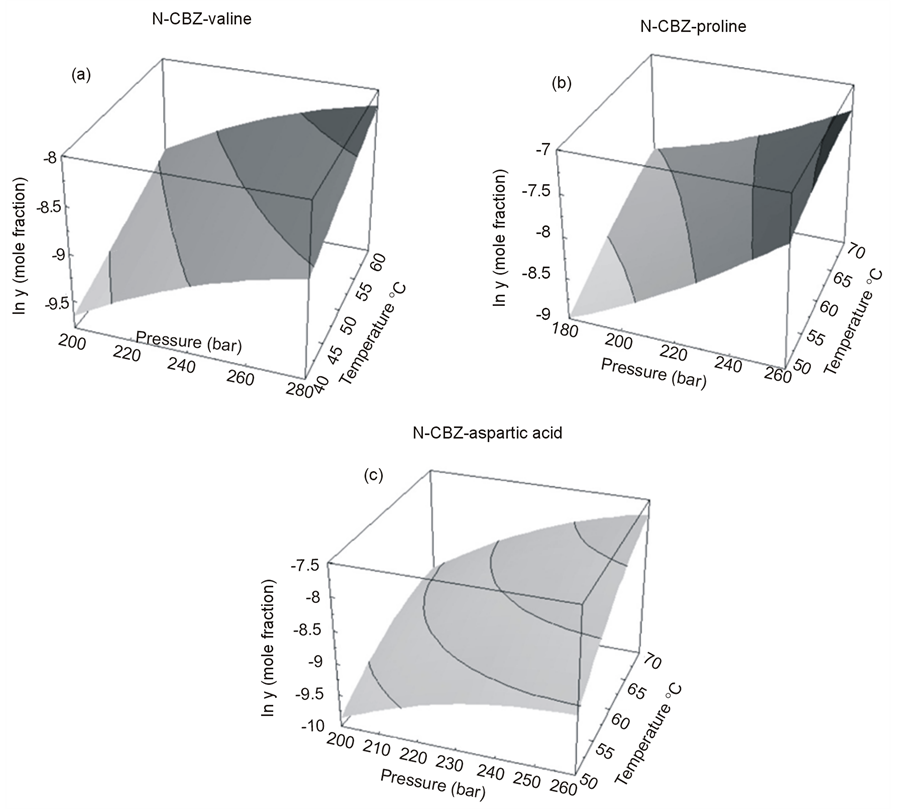
Figure 2. Model plot obtained using Gordillo and co-workers showing effect of pressures and temperatures on solubility of amino acids (a) N-CBZ valine; (b) N-CBZ-proline and (c) N-CBZ-aspartic acid in supercritical CO2.
Table 5. The coefficients of the equation Gordillo and coworker, 2004 model for the correlation of the solubility of the derivatized amino acids.
Table 6. Correlation of the experimental solubility to the predicted models of both Yu et al. and Gordillo models.
7. Summary and Conclusion
An attempt was made on correlation of the experimental solubility of the derivatized N-CBZ amino acids using theoretical models based on SRK-EOS with mixing rules proposed by Soave and empirical models proposed by Yu et al. (1999) and Gordillo (2004) using software. Soave modified Redlich-Kwong EOS based showed varied % AARD for the critical properties arrived by group contribution methods as high as 59% for N-CBZ-valine, while for N-CBZ-proline and N-CBZ-Aspartic acid it is reasonable limits of <20%. Between the models Yu and Gordillo, the Yu model has an % AARD up to 12%, while the best fit was observed using Gordillo empirical model % AARD up to 1.2%. Hence, it can be concluded that this model can be effectively used for and prediction of experimental solubility of naturally occurring biologically active compounds that are generally more polar.
Acknowledgements
Mr. Pravin Gadkari acknowledges the CSIR, New Delhi for the award of the Senior Research Fellowship. Directors of CSIR-CFTRI and CSIR-CLRI are acknowledged for their encouragement and support for this work.
References
- Caude, M. and Thiebaut, D. (1999) Practical Supercritical Fluid Chromatography and Extraction. Harwood Academic Publishers, Chur.
- Erkey, C. (2000) Supercritical Carbon Dioxide Extraction of Metals from Aqueous Solutions: A Review. Journal of Supercritical Fluids, 17, 259-287. http://dx.doi.org/10.1016/S0896-8446(99)00047-9
- Laintz, K.E., Wai, C.M., Yonker, C.R. and Smith, R.D. (1992) Extraction of Metal Ions from Liquid and Solid Materials by Supercritical Carbon Dioxide. Analytical Chemistry, 64, 2875-2878. http://dx.doi.org/10.1021/ac00046a039
- Wai, C.M. (1995) Supercritical Fluid Extraction of Trace Metals from Solid and Liquid Materials for Analytical Applications. Analytical Sciences, 11, 165-167. http://dx.doi.org/10.2116/analsci.11.165
- Lin, Y., Brauer, R.D., Laintz, K.E. and Wai, C.M. (1993) Supercritical Fluid Extraction of Lanthanides and Actinides from Solid Materials with a Fluorinated β-Diketone. Analytical Chemistry, 65, 2549-2551. http://dx.doi.org/10.1021/ac00066a027
- Iso, S., Uno, S., Meguro, Y., Sasaki, T. and Yoshida, Z. (2000) Pressure Dependence of Extraction Behaviour of Plutonium (IV) and Uranium (VI) from Nitric Acid Solution to Supercritical Carbon Dioxide Containing Tributyl Phosphate. Progress in Nuclear Energy, 37, 423-428. http://dx.doi.org/10.1016/S0149-1970(00)00082-2
- Tomioka, O., Meguro, Y., Enokida, Y., Yamamoto, I. and Yoshida, Z. (2001) Dissolution Behaviour of Uranium Oxides with Supercritical CO2 Using HNO3-TBP Complex as a Reactant. Journal of Nuclear Science and Technology, 38, 1097-1102. http://dx.doi.org/10.1080/18811248.2001.9715141
- Mincher, B.J., Fox, R.V., Holmes, R.G.G., Robbins, R.A. and Boardman, C. (2001) Supercritical Fluid Extraction of Plutonium and Americium from Soil Using Theonytrifluoroacetone and Tributylphosphate Complexation. Radiochimica Acta, 89, 613-617.
- Lin, Y., Wai, C.M., Jean, F.M. and Brauer, R.D. (1994) Supercritical Fluid Extraction of Thorium and Uranium Ions from Solid and Liquid Materials with Fluorinated beta Diketones and Tributyl Phosphate. Environmental Science and Technology, 28, 1190-1193. http://dx.doi.org/10.1021/es00055a034
- Rao, A., Kumar, P. and Ramakumar, K.L. (2010) Separation of Uranium from Different Uranium Oxide Matrices Employing Supercritical Carbon Dioxide Extraction. Journal of Radioanalytical and Nuclear Chemistry, 285, 247-257. http://dx.doi.org/10.1007/s10967-010-0568-7
- Smart, N.G., Carleson, T., Kast, T., Clifford, A.A., Burford, M.D. and Wai, C.M. (1997) Solubility of Chelating Agents and Metal Containing Compounds in Supercritical Fluid Carbon Dioxide. Talanta, 44, 137-150. http://dx.doi.org/10.1016/S0039-9140(96)02008-5
- Kumar, R., Sivaraman, N., Senthil Vadivu, E., Srinivasan, T.G. and Vasudeva Rao, P.R. (2003) Complete Removal of Uranyl Nitrate from Tissue Matrix Using Supercritical Fluid Extraction. Radiochimica Acta, 91, 197-201. http://dx.doi.org/10.1524/ract.91.4.197.19966
- Kumar, R., Sivaraman, N., Sujatha, K., Srinivasan, T.G. and Vasudeva Rao, P.R. (2007) Removal of Plutonium and Americium from Waste Matrices by Supercritical Carbon Dioxide Extraction. Radiochimica Acta, 95, 577-584. http://dx.doi.org/10.1524/ract.2007.95.10.577
- Suresh Kumar, V., Kumar, R., Sivaraman, N., Ravisankar, G. and Vasudeva Rao, P.R. (2010) Design and Adaptation of a Novel Supercritical Extraction Facility for Operation in a Glove Box for Recovery of Radioactive Elements. Review of Scientific Instruments, 81, 094101-094106. http://dx.doi.org/10.1063/1.3484190
- Kumar, R., Sivaraman, N., Sujatha, K., Srinivasan, T.G. and Vasudeva Rao, P.R. (2009) A Novel Technique for Modifier Free Delivery of Ligands for Supercritical Fluid Extraction. Radiochimica Acta, 97, 443-451. http://dx.doi.org/10.1524/ract.2009.1633
- Sujatha, K., Pitchaiah, K.C., Sivaraman, N., Srinivasan, T.G. and Vasudeva Rao, P.R. (2012) Recovery of Uranium and Plutonium from Waste Matrices Using Supercritical Fluid Extraction. American Journal of Analytical Chemistry, 3, 916-922. http://dx.doi.org/10.4236/ajac.2012.312A121
- Sujatha, K., Pitchaiah, K.C., Sivaraman, N., Nagarajan, K., Srinivasan, T.G. and Vasudeva Rao, P.R. (2014) Recovery of Plutonium from Polymeric Waste Matrices Using Supercritical Fluid Extraction. Desalination and Water Treatment, 52, 470-475. http://dx.doi.org/10.1080/19443994.2013.808729
- Brahmmananda Rao, C.V.S., Srinivasan, T.G. and Vasudeva Rao, P.R. (2012) Studies on the Extraction by Substituted Butyl Phosphonates. Solvent Extraction and Ion Exchange, 30, 262-277. http://dx.doi.org/10.1080/07366299.2011.639250
- Datta, A., Sivaraman, N., Srinivasan, T.G. and Vasudeva Rao, P.R. (2011) Liquid Chromatographic Behaviour of Actinides and Lanthanides on Monolith Supports. Radiochimica Acta, 99, 275-283. http://dx.doi.org/10.1524/ract.2011.1816
- Suresh, A., Srinivasan, T.G. and Vasudeva Rao, P.R. (1994) Extraction of U(VI), Pu(IV) and Th(IV) by Some Trialkyl Phosphates. Solvent Extraction and Ion Exchange, 12, 727-744. http://dx.doi.org/10.1080/07366299408918234
Nomenclature
a, b EOS mixture parameter kij, nij binary interaction parameter P pressure Pc critical pressure R universal gas constant T temperature Tc critical temperature TB normal boiling point temperature Mw molecular weight of the compound
ΔTL group Contributions for temperature in Lydersen equation
ΔVL group Contributions for volume in Lydersen equation Vc critical volume
ΔBJ group Contributions for boiling point
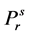 reduced vapor pressure
reduced vapor pressure
 fugacity of solute in the solid phase
fugacity of solute in the solid phase
 fugacity of solute in the gas phase
fugacity of solute in the gas phase
v, V molar volume y, y2 mole fraction in supercritical phase
Greek Letters
φ fugacity coefficient
ω acentric factor
ρ density
Subscripts
c critical i, j component indices cal calculated value pre predicted value
Superscripts
sat saturated value sub sublimation
Abbreviations
AARD averageabsolute relative deviation EOS equation of state SRK Soave-Redlich-Kwong SCF Supercritical fluid
NOTES

*Corresponding author.


