Received 12 March 2016; accepted 9 April 2016; published 12 April 2016

ABSTRACT

There exist many ways to measure financial asset volatility. In this paper, we introduce a new joint model for the high-low range of assets prices and realized measure of volatility: Realized CARR. In fact, the high-low range and realized volatility, both are efficient estimators of volatility. Hence, this new joint model can be viewed as a model of volatility. The model is similar to the Realized GARCH model of Hansen et al. (2012), and it can be estimated by the quasi-maximum likelihood method. Out-of-sample volatility forecasting using Standard and Poors 500 stock index (S&P), Dow Jones Industrial Average index (DJI) and National Association of Securities Dealers Automated Quotation (NASDAQ) 100 equity index shows that the Realized CARR model does outperform the Realized GARCH model.

Keywords:

High-Low Range, Realized Volatility, Joint Model, High Frequency Data

1. Introduction

Modeling the volatility of financial asset returns is of fundamental importance to option pricing, assets portfolio and risk management. Many ways exist to model financial asset volatility, such as ARCH/GARCH family of models and stochastic volatility (SV) model. The strength of these models lies in their flexible adaptation of the dynamics of volatility. With the increasing availability of high frequency financial data, considerable literature on the use of intra-day as set price data to measure daily volatility has been expanded. The research has introduced many realized measures of volatility, such as realized variance [1] , bipower variation [2] , realized kernel [3] , and many other quantities. Any of these realized measures of volatility contains much information about the current level of asset price volatility than the squared daily return. This makes them widely used in the recent research of financial economics. However, in the real world, the realized measure of volatility is vulnerable contaminated by the presence of non-trading hours and the market microstructure noise.

In practice, the daily return is less subject to the market microstructure noise but contains less information of volatility, while the realized volatility is heavily contaminated by the noise but still includes much information. In this context, recently, numerous researchers have devoted to study the joint model for daily returns and realized measure of volatility. The joint model can be classified into two categories according to different points of view. We will describe the two kinds of joint model in details in the following paragraph.

The first kind of the joint model is MEM (Multiplicative Error Model) and HEAVY (High-Frequency-Based Volatility Model) models, which deal with multiple latent volatility processes. The first joint model is introduced by Engle and Gallo (2006) [4] , known as the MEM model [5] . Three measures of volatility, including absolute return, range and realized volatility, are combined in the MEM model. An alternative model is the HEAVY model proposed by Shephard and Sheppard (2010) [6] . The other kind model is based on the structure of the GARCH and SV model with an observation equation and a measurement error. In this sense, Hansen et al. (2012) propose a Realized GARCH model within the context of GARCH model [7] . The key feature of the Realized GARCH model is a measurement equation which can relate the realized volatility to the conditional variance of returns [7] . Based on the SV (stochastic volatility) model, Takahashi et al. (2009) introduce a joint model named as RV-SV model or Realized SV model [8] . The advantage of the Realized GARCH model is that it can be estimated by quasi-maximum likelihood method, while the Realized SV model requires more complicated algorithms. Some other extended joint models are discussed in Hansen and Huang (2012) [9] , Hansen et al. (2012) [10] , etc.

The high-low range of daily return is an alternative way of measuring volatility; Parkinson (1980) showed that the high-low range is a more efficient estimator of volatility than the daily return, because the formation of the range is from the entire price process [11] . Many other researchers extend the high-low range estimator to include more information, such as the opening and closing prices. Due to the efficiency of the high-low range estimator, the high-low range can also be used to reduce the microstructure noise in high-frequency data field. Martens and Van Dijk (2007) [12] and Christensen and Podolskij (2007) [13] provided a more efficient estimator realized range-based variance, which is formed from replacing each squared return by the high-low range. It is a puzzle that the theory and the simulation results of the high-low range estimator perform well, while the empirical application performs poorly, due to its failure to capture the dynamic of volatilities. For this reason, Chou (2005) proposed a range-based volatility model named CARR (Conditional Autoregressive Range model), which can appropriately model the dynamic of the high-low range [14] . Brandt and Jones (2006) [15] , among others, extended the CARR model to the time series EGARCH model, and draws a conclusion that the range- based time series model outperforms than the daily return in empirical analysis. The CARR model has been extended much more; other references include Chiang and Wang (2011) [16] , Lin et al. (2012) [17] , etc.

In this paper, we will introduce a new joint model which combines a CARR model for range with realized volatility, named realized CARR model. Comparing with the first joint MEM model, this new joint realized CARR model gives up the shortcoming of it that deals with three latent volatility processes. Meanwhile, the new model retains the superiority of the realized GARCH model which contains only two latent volatility processes, while more informative than the latter. The model proposed by this paper can be used to calculate Value-at-Risk and Expected Shortfall which are helpful for financial risk managers and portfolio managers.

The structure of this article is as follows. In Section 2, we first give a review of the CARR model and Realized GARCH model, and then we propose the Realized CARR model. The estimation of the Realized CARR model is described in Section 3. The results of the simulation for Realized CARR model are show in Section 4. In Section 5, we apply our model to Standard and Poors 500 stock index, Dow Jones Industria Average index (DJI) and National Association of Securities Dealers Automated Quotation (NASDAQ) 100 equity index, and provide out-of-sample forecasting comparison between the Realized CARR and Realized GARCH model. The Section 6 concludes the paper.

2. Realized CARR

In this section, we introduce the Realized CARR model. We start with a brief of the CARR and the Realized GARCH model which provide the motivation for our introduced joint model.

2.1. The CARR Model

Let 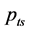be the logarithmic price of an asset at time 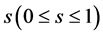on day. In the paper of Chou (2005) [14] , 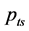is supposed to be driven by a geometric Wiener process. Then the high-low range of the return is defined as:

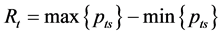(1)

where 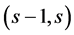is the interval of range measurement which is normalized to be unity.

The CARR (p, q) model is first introduced by Chou (2005), which is specified as:

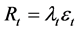(2)

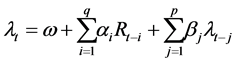(3)

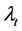is the conditional mean of the high-low range determined by the information set 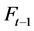which contains all the past information of asset price up to time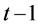. 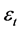is the innovation term assumed to have a non-negative support distribution with a unit mean: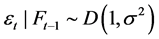. From the result of Chou (2005) [14] , if the innovation is i.i.d., the variance of the innovation 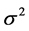is proportional to the square of the ranges’ conditional expectation. While, if not, the variance 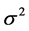is unknown and time-varying but can be specified. The parameters 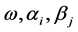in the CARR model are all positive to ensure positivity of. In order to ensure stationarity of the process, the parameters are assumed to satisfy the following requirement:. The CARR model is extended from GARCH model, the parameters in both model have the same meaning. A discussion of the parameters can be seen in Bollerslev (1986) [18] .

2.2. Realized GARCH Model

The template is used to format your paper and style the text. All margins, column widths, line spaces, and text fonts are prescribed; please do not alter them. You may note peculiarities. For example, the head margin in this template measures proportionately more than is customary. This measurement and others are deliberate, using specifications that anticipate your paper as one part of the entire journals, and not as an independent document. Please do not revise any of the current designations.

The Realized GARCH model proposed by Hansen et al. (2012) [7] is a joint model for daily return and realized volatility. The structure of the Realized GARCH (p, q) model is specified as:

(4)

(5)

(6)

In this model, is the return, denotes a realized measure of volatility. is the conditional variance of the return, , where is the past information of asset price up to time t-1. The disturbance terms and are assumed to be mutually independent, and. represents the leverage effect and is given by:.

The first two equations (4) and (5) are referred as the return equation and the GARCH equation, see Hansen et al. (2012) [7] for details. The last equation (6) named as measurement equation reveals that the realized volatility can be decomposed into conditional variance and a noise term which denotes the influence of market microstructure noises. It is reasonable that is an accurate measurement of asset price volatility.

2.3. Realized CARR Model

Motivated by the CARR model of Chou (2005) [14] and the Realized GARCH model by Hansen et al. (2012) [7] , we introduce the following Realized CARR model:

(7)

(8)

(9)

and have the same meaning with the CARR model, while, have the same meaning as the Realized GARCH model. is assumed to have a non-negative support distribution with a unit mean, a natural choice is the unit exponential. In this model, is given by, and. In this model, we don’t consider the leverage effect, which can be characterized by introducing daily returns, realized semi variance or indicator functions [4] [14] [19] . And we will leave this leverage effect for further study.

The CARR model is similar to the ACD model by Engle and Russell (1998) [20] , and is a generalization of the MEM model in Engle (2002) [5] , Engle and Gallo (2006) [4] . While, there are critical differences between the CARR and the ACD model, see Chou (2005) [14] . In the Realized CARR model, is the daily range, while it can be replaced by other non-negative variables, such as volumes, absolute returns, trades, etc. The CARR model is a particular case of the MEM model. In this sense, the Realized CARR model also can be extended as Realized MEM model.

3. Model Estimation

In this section, we will introduce the estimation of the Realized CARR model. By the results of Chou (2005) [14] , the CARR model can be ease estimated by the Quasi-Maximum Likelihood Estimation. The model estimation can be obtained by setting a GARCH model for the square root of range and taking the mean to zero. In this sense, the estimation of the Realized CARR model can be obtained by estimating the Realized GARCH model with a specification like the CARR model. So the analysis of the Quasi-Maximum Likelihood Estimation (QMLE) will be similar to the Realized GARCH model, the standard GARCH model and the CARR model. According to Engle and Gallo (2006) [4] , Shephard and Sheppard (2010) [6] and Hansen et al. (2012) [7] , the joint likelihood can be decomposed and be maximized separately. The key points about the likelihood factorization are that the innovations (,) in the model are supposed to be independent and the variables (high-low range, realized volatility) are assumed to relaying on their own latent volatility process.

Although the estimation of the Realized CARR model is similar to the Realized GARCH model, it is still somewhat different. In the following paragraph, we will describe the structure of QMLE analysis for the Realized CARR model. The first and second derivatives of the log likelihood function are provided in this section.

The log-likelihood function is specified as:

(10)

According to Hansen et al. (2012), the joint conditional density can be factorized as:

(11)

In the model, , and, the joint likelihood can be spited into the sum:

In the estimation of the joint model, we can ignore the constant term which does not affect the parameter estimation. Therefore, the likelihood function can be abbreviated to:

(12)

Before taking derivatives, we simplify the joint model by:

(13)

(14)

where, , and,. .

Then, we will provide the first and second derivatives of the log-likelihood function.

Lemma 1. Define, , where, otherwise, and. , which is a matrix. Then

(15)

(16)

Proposition 2. 1) The first derivative of the log-likelihood function, is given by

(17)

where.

2) The second derivative, , is specified as:

where and.

The details of Lemma 3.1 and Theorem 3.2’s proof can be seen in Hansen et al. (2012) [7] , which are omitted in this dissertation.

According to the corollary of Lee and Hansen (1994) [21] and the Proposition 3 of Hansen et al. (2012) [7] , the maximize of log-likelihood function will be consistent and asymptotically normal and the model can be estimated with the realized GARCH model procedure by making as the dependent variable and setting the mean is zero (see Engle (2002) [5] ). More discussions about this topic can be seen in Hansen et al. (2012) [7] .

4. Simulation

We will show the simulation results of Realized CARR (1,1) model in this section. In order to understand the performance of the model, we use two parameter settings in this simulation and set the sample size as T = 1000, 1500 and 2000. Two parameter settings: Case 1,; Case 2,. The simulation results for two parameter cases are shown in Table 1 and Table 2.

The results of the simulation for Realized CARR (1,1) model indicate that the model performs well and isn’t affected by the initial values. Therefore, the estimation method of this model is very robust.

5. Empirical Application

In this section, we introduce the empirical analysis of our proposed model using daily range data, returns and realized measures for Standard and Poors 500 stock index (S&P), Dow Jones Industria Average index (DJI) and National Association of Securities Dealers Automated Quotation (NASDAQ) 100 equity index. The in sample period is from January 3, 2005 to August 30, 2013 and out of sample period is from September 2, 2013 to December 31, 2013. These data are downloaded from Oxford-Man Institute of Quantitative Finance Realized Library (Library Version: 0.2 [22] ). From the Realized Library, we can download several types of realized volatilities, such as RV, RK, BRV (Bipower Variation), MTRV (Median Truncated Realized Variance), RSRV (Realized Semi-variance) et al. In order to reduce the microstructure noise, in this paper, we adopt the realized kernel (RK) proposed by Barndor-Nielsen et al. (2008) [3] as the realized measure.

5.1. Data Description

Before estimation, we give the description of the sample data. Figures 1-3 show the time plot of the daily range, returns, realized kernel, log realized kernel and Tables 3-5 present the descriptive statistics for these data. The skewness and kurtosis show that the realized kernel is not normal but its logarithm is nearly normal, so we use logarithmic realized kernel data rather than realized kernel in this paper. The Jarque-Bera (JB) statistic is to test the normality of the sample data and its critical value is 5.99 (5%), which indicates the non-normal distribution of the sample data. It might be better to assume the distribution of non-normal, which we will leave for future study. The Ljung-Box (LB) test is a statistical test for autocorrelations of a time series. LB (10) is the Ljung-Box statistic with 10 lags and its critical value is 18.31 (5%). According to the LB (10) statistic, the daily return and high-low range of the sample data are non-auto correlated and non-white volatilities.

It might be better to assume the distribution of ut non-normal, which we will leave for future study. The Ljung-Box (LB) test (see Diebold (1988) [23] ) is a statistical in this paper test for autocorrelations of a time series. LB (10) is the Ljung-Box statistic with 10 lags and its critical value is 18.31 (5%). According to the LB (10) statistic, the daily return and high-low range of the sample data are non-auto correlated and non-white volatilities.

As is shown in the time plots of all the sample data, the financial assets have high volatilities during the financial crisis. The sample should be divided into pre and post financial crisis periods which indicate a regime switching model is needed. This is out of scope for the purposes of this article and we will leave this for further research.

5.2. Data Description

The details of model estimation results are presented in this section. According to the plot of partial autocorrelation (PACF) and autocorrelation function (ACF), we determine the order of the two models as GARCH (1,1) and CARR (1,1). And in a practical application, the model GARCH (1,1) and CARR (1,1) are sufficient for most of the asset returns (see Bollerslev et al. (1992) [24] , Chou (2005) [14] ). As Hansen et al. (2012) [7] have shown that the realized GARCH model is superior to GARCH model, there is no need to compare our model with GARCH model. Hence, in this section, we just estimate the Realized CARR (1,1) and Realized GARCH (1,1) models. The estimation results of the two models are reported in Table 6.

In order to compare the estimated models, we calculate the Akaike information criterion (AIC) and Schwarz information criterion (SC) according to the following formulas:

where denotes the log-likelihood and k is the number of parameters in the statistical model. The criteria is that the minimum AIC and SC values, the better a model is.

As is shown in Table 6, AIC and SC values of the S&P data are the smallest in all of the sample data in both models, while they are the highest values in Nasdaq data. AIC and SC values of the realized CARR model are both smaller than that of realized GARCH model, that is to say, the former model has a better fitting effect than the latter. The sum of parameters and of realized CARR is 0.961, 0.910 and 0.938, while the sums of realized GARCH model are 0.982, 0.920, 0.959. As we can see, the sum of realized CARR are all smaller than the latter’s which means the realized CARR model can reduce the persistence of volatility. This is consistent with the rule of information criteria.

Figure 4 is the residual density of realized CARR (1,1) model of sample s&p. The other two samples’ plots of residual density of the realized model are similar with sample s&p’s and we omit them here. As we can see, the

shape of the empirical distribution diverges from the exponential density whose function is monotonically decreasing. It is consistent with the descriptive statistics as showed in Table 3. The phenomenon of this distribution is named heavy tail which we will leave for further study.

5.3. Out-of-Sample Volatility Forecast Comparison

To assess the forecasting power of realized CARR model, we perform out-of-sample forecasts and make comparisons with realized GARCH model. We choose the forecast horizons to be from 1 day to 80 days which is from September 2, 2013 to December 31, 2013. Two ex post volatilities: daily return squared (DRSQ) and daily high-low range (DHLR) are used as measures in this paper. Then the root-squared (RMSE) and the mean-abso- lute-errors (MAE) are computed to compare the forecasting power of realized CARR model with realized GARCH model. RMSE and MAE are defined as:

where h means the forecast horizon, MV and FV denote the measure volatility and forecasted volatility, respectively.

Rolling samples of 2173 observations are used to modeling the two models and 100 data are made for out-of- sample forecast. The Table 7 is the result of Out-of-Sample Forecast Comparison for Realized CARR (1,1) and Realized GARCH (1,1), where RC denotes the realized CARR model and RG represents the realized GARCH model. Table 7 shows that the two forecast evaluation criteria give almost unanimous support for realized CARR model over realized GARCH model. For all case, RMSE and MAE of realized CARR model are smaller than that of realized GARCH model. It is not surprising that the realized CARR model contains more information and yield more precise in forecast comparisons.

Table 8 is the test of Mincer-Zarowitz regression and the null hypothesis is and. F is the test statistic with critical value 3.01 (5%) From the test results can be seen that all the realized GARCH models of sample data reject the null hypothesis while all the realized CARR accepts the null hypothesis. The results of Mincer-Zarowitz regression tests are consistent with the two forecast evaluation criteria.

6. Conclusion

In this paper, we introduce a new joint model for the high-low range of assets prices and realized measure of volatility: Realized CARR. The model is easy to be estimated by the quasi maximum likelihood method. The empirical results show the superiority of fitting volatility than the realized GARCH model and it yields more precise in forecast comparisons. The new joint model gives up the shortcoming of MEM, which deals with multiple latent volatility processes, but retains the superiority of the realized GARCH model which contains only two latent volatility processes, while more informative than the latter. The model proposed by this paper can be

used to calculate Value-at-Risk and Expected Shortfall which are helpful for financial risk managers and portfolio managers. In fact, we only give the most general form of the model which can be extended much more, such as includes leverage effect, exogenous variables, heavy tail, regime switching, etc., which we leave for further study.

Acknowledgements

This work is supported by the Guangxi China Science Foundation (2014GXNSFAA118015) and the Scientific Research Project of Guangxi Colleges and Universities (KY2015ZD054).

Cite this paper

Yunqian Ma,Yuanying Jiang, (2016) Modeling and Forecasting Financial Volatilities Using a Joint Model for Range and Realized Volatility. Open Journal of Business and Management,04,206-218. doi: 10.4236/ojbm.2016.42022

References

NOTES

^*Corresponding author.