Advances in Materials Physics and Chemistry
Vol.07 No.06(2017), Article ID:77017,14 pages
10.4236/ampc.2017.76021
Scanning Based Induction Heating for AISI 4340 Steel Spline Shafts-3D Simulation and Experimental Validation
Habib Hammi, Abderrazak El Ouafi, Noureddine Barka, Ahmed Chebak
Mathematics, Computer Science and Engineering Department, University of Quebec at Rimouski, Rimouski, Canada

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: March 18, 2017; Accepted: June 17, 2017; Published: June 20, 2017
ABSTRACT
This paper presents an investigation of non-stationary induction heating process applied to AISI 4340 steel spline shafts based on 3D simulation and experimental validation. The study is based on the knowledge, concerning the form of correlations between various induction heating parameters and the final hardness profile, developed in the case of stationary induction heating. The proposed approach focuses on analyzing the effects of variation of frequency, power and especially scanning speed through an extensive 3D finite element method simulation, comprehensive sensitivity study and structured experimental efforts. Based on coupled electromagnetic and thermal fields analysis, the developed 3D model is used to estimate the temperature distribution and the hardness profile. Experimentations conducted on a commercial dual-frequency induction machine for AISI 4340 steel splines confirm the feasibility and the validity of the proposed modelling procedure. The 3D model validation reveals a great concordance between simulated and measured results, confirms that the model can effectively be used as framework for understanding the process and for assessing the effects of various parameters on the hardening process quality and performance and consequently leads to the most relevant variables to use in an eventual hardness profile prediction model.
Keywords:
Induction Heating, Non-Stationary Induction Heating, Spline Shafts, Hardness Profile, Temperature Distribution, Finite Element Method, Induction Heating Parameters, Sensitivity Study, Prediction Model

1. Introduction
Many industries today, especially aerospace and automotive manufacturers, require parts that are reliable in term of fatigue life and resistance. A spline, for example, is exposed for the majority of its lifetime to corrosion, loads, friction, wear, etc. To address these problems, engineers have introduced processing plans that aim not only to harden the part, but also to extend its lifetime so as to increase the reliability of the mechanical products.
One of the best processes is induction hardening, which is used to bond, harden or soften metals or other conductive materials. It offers an attractive combination of speed, consistency and control. The basic principle of induction heating has been applied since the 1920s, and during World War II, the technology has been developed rapidly to meet the urgent wartime requirement for a fast and reliable process to harden metal engine parts. What makes induction heating unique is the contactless heat transfer between the coil and the part, and most importantly the speed of the process. Induction heating relies on radio frequency (RF) energy, so heat is transferred to the part via electromagnetic waves and the inductor itself does not get hot. This leads to a highly repeatable and reliable process.
When an alternating current is applied to the primary coil of a transformer, an alternating magnetic field is created. According to Faraday’s Law, if the secondary coil of the transformer is located within the magnetic field, an electric current will be induced. In our setup, the coil is the primary winding of the transformer and the part, located inside the electromagnetic field, is the secondary winding of the transformer. Therefore, circulating eddy currents are induced within the part in question. These eddy currents flow against the electrical resistivity of the metal, generating localized heat. This heating is called the Joule effect, referring to Joule’s first law. In induction heating process, there is no contact between the inductor and the part, and therefore no combustion gases. The material to be heated can be located in a setting isolated from the power supply: submerged in a liquid, covered by isolating substances, in gaseous atmospheres or even in a vacuum.
Induction heating of the surface presents several advantages over other heat treatment methods, including high repeatability regarding the hardened layer quality, short heat treatment times, and easy incorporation into automated manufacturing processes [1] . Adding to that, compressive residual stresses are generated along with the hardened depth after induction hardening [2] . The efficiency of an induction heating system for our application depends on several factors: the used frequency, the capacity of the power supply, and most importantly, the scanning speed. The induction heating of splines was previously evoked in the work done by the authors, but in this case the spline was stationary and there was no scanning involved [3] [4] . All of the induced power and heat were concentrated in a single region in the spline.
In this work, 3D modelling and simulation, structured experimental efforts and improved statistical analysis tools are used to evaluate the effects of power, frequency variation and particularly scanning speed on the hardness profile. The model experimental validation is conducted on a commercial dual-frequency induction machine for AISI 4340 steel splines. The validated 3D model is used to simulate various process parameters and conditions effects and to estimate the temperature distribution as well as the hardness profile attributes. ANOVA is also used to evaluate the contribution of each parameter in temperature and hardness profile attributes variations. Based on these results, predictive models are established.
2. 3D Modelling Development
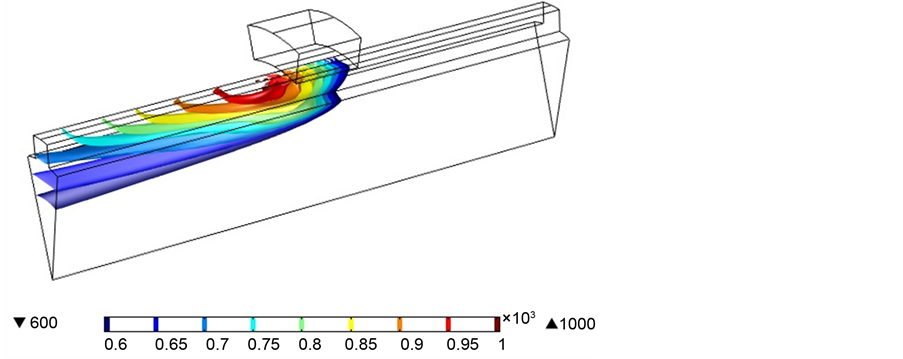
The spline used in this work is made out of AISI 4340 steel which is the best used for splines, gears, shafts, and other structural parts. The spline has a 25 mm diameter with an internal diameter of 21 mm and is enrolled with a 27 mm coil made of copper as illustrated in “Figure 1”. Hence, the gap between the part and the coil is fixed at 1 mm. The spline should be moving along z-axis with a velocity V that we will vary to study velocity effects on hardened profile. The hardened region is supposed to be inside the electromagnetic considering the part motion. Because the spline is composed of 12 teeth, and thanks to the circular symmetry, only one twelfth of the spline is studied by simulation. This will shorten the calculation time and the software efforts to give precise results [5] [6] [7] [8] [9] .
2.1. Parameters Control
A convergence study was conducted and revealed that the best mesh size in terms of calculation time and precision of results is equal to 0.5 mm. The power delivered by the coil was varied around 26 kW. Many tests were done to find that a proper hardness profile starts to appear with values greater than 23 kW. A frequency of 200 kHz was chosen for the simulation and the scanning speed was set to V = 10 mm/s. This resulted in a hardened region as the temperature reached the level needed for austenite formation, followed by a hardened layer with the formation of martensite after quenching.
Figure 1. 3D Spline model with dimensions (in mm) and temperature distribution (in ˚C).
The materials used in the simulation were air for the surroundings, cooper for the coil, and AISI 4340 steel for the spline. The AISI 4340 steel is characterized by a relative permeability, an electrical conductivity, a heat capacity and a thermal conductivity that are determined as a function of temperature over a specific time lapse during the simulation. Four interpolation functions were established to control the electromagnetic properties of the AISI 4340 steel. External current density was applied to the coil, and its geometric vector has x-axis and a y-axis coordinates in the 3D space. COMSOL Multiphysics software was used to solve Maxwell’s equations which can be written as follows:
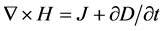 (1)
(1)
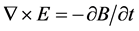 (2)
(2)
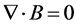 (3)
(3)
 (4)
(4)
where E is electric field intensity, D is electric flux density, H is magnetic field intensity, B is magnetic flux density, J is conduction current density, and  is electric charge density. Special symbols like
is electric charge density. Special symbols like 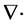 and
and 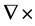 are popular in vector algebra and are useful to reduce an expression of particular differential operation without having to carry out the details:
are popular in vector algebra and are useful to reduce an expression of particular differential operation without having to carry out the details: ,
, 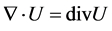 and
and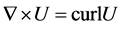 . In this part, we used the Fourier equation as it is written in this form:
. In this part, we used the Fourier equation as it is written in this form:
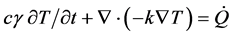 (5)
(5)
where T is temperature,  is the mass density of the metal, c is the specific heat, k is the thermal conductivity of the metal and Q is the heat source density induced by eddy currents per unit time in a unit volume. The system to be solved is given by:
is the mass density of the metal, c is the specific heat, k is the thermal conductivity of the metal and Q is the heat source density induced by eddy currents per unit time in a unit volume. The system to be solved is given by:
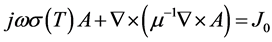 (6)
(6)
 (7)
(7)
where 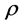 is the mass density,
is the mass density, 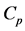 is the specific heat capacity and J0 is the source current density. The translational motion is described by Equation (5) and a dynamic vector u that can be written as:
is the specific heat capacity and J0 is the source current density. The translational motion is described by Equation (5) and a dynamic vector u that can be written as:
 (8)
(8)

One of the major features of induction heating computation deals with the fact that both the electromagnetic and the heat transfer phenomena are tightly coupled thanks to the interrelated nature of the material properties. First, specific heat, thermal conductivity, and electric resistivity are functions of the temperature. Second, magnetic permeability is a function of magnetic field intensity, temperature, and frequency. The multiphysics and the coupling aspects of the application are described by the system of equations below.




In this system of equations, both electric and magnetic fields are described, as well as the equation that links them to the heat produced. Scanning velocity is also shown and has an effect on the heat induced in the spline.
2.2. Martensitic Formation
The simulation was done using the mesh size, frequency, induced current density, and velocity most suitable for producing the proper hardened profile. However, before analyzing the results, some theoretical study of microstructure should be done.
AISI 4340 alloy steel is a low alloy steel that contains iron (95.195% - 96.33%), nickel (1.65% - 2%), chromium (0.7% - 0.9%), manganese (0.6% - 0.8%), carbon (0.37% - 0.43%), molybdenum (0% - 2% - 0.3%), silicon (0.15% - 0.3%), sulfur (0.04%) and phosphorous (0% - 0.35%). This steel is heat treated above 830˚C followed by quenching in oil. It is used mainly in power transmission gears and shafts, aircraft landing gears, and other structural parts. The AISI 4340 steel has a raw non-martensitic microstructure that appears in “Figure 2”, bottom right. This structure is characterized by its ease of bending under high stresses and its easiness to be corrosive. After the induction hardening is applied, a fine hardened surface layer appears showing a martensitic microstructure that is seen in “Figure 2”, top right. Martensite is formed in carbon steels by the rapid cooling (quenching) of austenite at a high enough rate that carbon atoms do not have time to diffuse out of the crystal structure in large enough quantities to form cementite (Fe3C). As a result, the face-centered cubic austenite transforms to a
Figure 2. Cross section of the Hardened spline tooth (left), microstructure of the Hardened surface (top right) and microstructure of the raw material (bottom right).
highly strained body-centered tetragonal form of ferrite that is supersaturated with carbon. The shear deformations that result produce large numbers of dislocations, which is the primary strengthening mechanism in steels.
3. Predicted versus Measured Results
The simulation was done with a frequency equal to 200 kHz and the results were good enough to understand the transformation and the temperature effects over the AISI 4340 spline microstructure.
3.1. Simulation Results
In “Figure 3”, temperature isothermal surfaces are shown to explain the heating penetration depth and the pattern described by the scanning movement. The red region is the region heated the most with more than 900˚C. That region undergoes martensitic transformation after fast quenching. That is the hardened region which will be exposed to stresses and continuous contact with other moving parts in the engine. The light blue region (from 650˚C to 800˚C) undergoes some transformation but not enough to reach austenite form and of course not to reach martensitic form after quenching.
For temperatures below 640˚C, no physical transformations are observed and the material remains in its bulk state. In fact, surface induction hardening process aims to harden the surface that is exposed to external efforts and fatigue and maintain the elastic properties of the spline heart so it will not bend under great pressure.
3.2. Predicted and Measured Results Comparison
Four set of simulations were done for validation with four heat-treated specimens. “Table 1”, presents the set parameters used in these simulations.
For each set of parameters, a simulation was done and temperature was measured along a line extending from the surface to the core of the spline. Due to the superficial aspect of induction heating, the temperature along this line
Figure 3. Isothermal surfaces showing different 3D levels.
starts at its highest value and decreases until all of the induced heat disappears. As the temperature decreases from 1000˚C, it first reaches the level where the austenite formation is completed (ds at Ac3 = 850˚C), followed by the level where austenite formation starts (dL at Ac1 = 825˚C), and finally the level where no physical transformation occurs (dc at T0 = 640˚C). To better visualize the temperature behavior, “Figure 4” shows temperature variation versus depth in the spline for each set of velocity and power parameters.
The predicted hardened case depth is measured from the intersection of the decreasing temperature curve and the 
The same sets of parameter values were applied to harden four specimens using induction machine. All four specimens reached martensitic formation after quenching, but with different case depths. For set A, the martensitic region had a case depth of 1.265 mm from the surface. A good hardened profile is visible and the entire tooth is transformed. For set B, the measured case depth is 0.98 mm, for set C it is 2.135 mm, and finally for set D it is 1.914 mm (see “Figure 5”). In the next paragraph, a comparison between simulated and measured hardness profiles is carried out for each of the four sets of parameter values. This is done to calculate the error rate and determine the precision and reliability of the 3D model.
3.3. Error Calculation and Model Precision
For each set of parameter values, 3D modeling and simulation using the finite element method and case depths experimental measurement are used to produce the hardness curve versus depth in the spline (see “Figure 6”). Theses curves are used to estimate the deviation between the predicted and the measured hardness and consequently to evaluate the precision and the efficiency of the prediction model.
The AISI 4340 spline has a high core hardness, 
Table 1. Sets A, B, C, and D definition for simulation and validation parameters.
Table 2. Hardened depths for the four sets of parameter values.
Figure 4. Temperature versus depth for power and velocity variation for sets (a)-(d).
Figure 5. Hardened specimens for set A, B, C, and D and measurement of the different hardened case depths.
the region is transformed to an austenitic phase because the temperature, T, is greater than



The four regions limits are calculated in “Table 2” for each set of parameter values using “Figure 4”. It is sufficient to calculate the x-axis coordinates of the intersections of the temperature curves and the three temperatures, 
Figure 6. Predicted and Measured Hardness versus depth for Sets (a)-(d).
and








The last region represents the material with unaffected microstructure. These three regions are illustrated in “Figure 6”. The spline is hardened at the surface, while core hardness does not change, which is normal in the case of surface treatments. The surface of the spline is the region in contact with other components, and therefore the region that will deteriorate first, hence the importance of having maximal hardness on the surface and through the skin depth. The data given in “Table 3” are used to draw the predicted and measured case depths versus sets of parameter values, shown in “Figure 7”. In the same figure, error is plotted to allow comparison with the two hardened depths. As we can see, the prediction models are very accurate. However, the predicted hardness in the spline is slightly short, in terms of depth, of the measured hardness only for set B. This is due to experimental measurements: in the simulation, only one twelfth of the spline is studied due to the symmetrical aspect of the model, but when the real spline was treated there were no edges because the spline was not cut, contributing to the miniscule discrepancy. The predicted and measured case depth are shown in the following table, and the error is calculated for each of the four sets.
Table 3. Simulation versus validation case depths for the four sets of values.
Figure 7. Predicted and measured case Depths, and errors versus Sets of values.
The best set result is for set C, as the drop in hardness is nearly identical for the predicted and measured cases. For a velocity V = 8 mm/s, P = 44%, and a frequency of 200 kHz, error is equal to 0.001 mm. These parameters thus prove a perfect combination for a perfect surface layer of martensite. This set can therefore be used for the sensitivity study in the following section.
4. Sensitivity Study and Behavioral Equations
A sensitivity study was conducted to determine the behavior of temperature as a function of frequency, power, and scanning velocity. One of the goals of such a study is to understand the influence of each parameter over the temperature. The contribution of each parameter was measured as a percentage. Frequency, power, and scanning velocity were changed between five levels, called scratching levels. ANOVA was used to establish the nonlinear equations describing temperature as a function of each parameter. This method helps to obtain the effects, relative weights, and relationships between the different process parameters.
4.1. Scratching Parameters Choice and Variation
The degree of variation for frequency, power and scanning velocity were, respectively, 10 kHz, 1%, and 1 mm/s. “Table 4” shows the scratching levels used in the sensitivity study. To analyze the effects, “Figure 8”, shows the mean temperature versus scratching parameters for each of the process parameters varied during the simulations and the tests.
4.2. Results and Interpretation
The effect of frequency over temperature is weak compared to the effects of power and velocity. In fact, a variation of ±10 kHz in frequency leads to nearly ± 25˚C. The calculated percent contribution of frequency to temperature is equal to 13.264%, as shown in “Table 5”. This weak effect is due to the fact that frequency is most responsible for skin depth and the penetration ratio. The frequency is only found in the equation for skin depth in the theoretical study of induction heating [3] [4] . Concerning power, a variation of ±1% leads to a variation of ±40˚C; the contribution is equal to 18.840%. The most influential process parameter is the scanning velocity. For low velocities at level 1 and level 2, an increase of 1 mm/s makes the temperature drop by nearly 75˚C. For level 4 and level 5 the drop is less drastic, with temperature decreasing only by 40˚C. This is due to the fact that the faster the spline is moving, the less time it is exposed to the electromagnetic fields induced from the coil, and therefore the lower is the temperature. For scanning induction heating process, researchers must study the scanning speed very carefully to better chose the most appropriate value needed for each individual application. The frequency value is most crucial when locally
Figure 8. Temperature means versus Scratching parameters for the frequency, the power, and the scanning velocity.
Table 4. Scratching parameters and their levels for the sensitivity study.
Table 5. Percent contribution of each parameter variation over the temperature.
heating a mechanical component in which the dimension of the martensitic layer is the most important. Stationary induction heating of splines and gears is a good example for better understanding the effects of frequency, as the equal heating of tips and roots constitutes a great challenge [3] [4] .
Concerning the power induced in the piece, the role of power has the same importance in every application. “Table 5” shows the contribution of machine parameters to temperature, calculated using the statistical software Minitab.
4.3. Behavioral Equations
In this study, data are implemented and used to find the equations that best describe the relationship between spline induction heating process responses and parameters. The equations link temperature, T, and the process parameters in their first, second, and third orders to best determine the nonlinearity of the model. The software used to calculate these equations is Minitab. The equation that links T to frequency, power and scanning velocity can be written as shown in Equation (14), for a linear form, and Equation (15), for a non-linear form.


Equation (14) presents the model based on linear regression and allows the evaluation of the case depth as a function of the three factors used in the sensitivity study. On the other hand, Equation (15) presents the model based on a non-linear regression study and includes the interaction between all of the factors. These equations are without units because they involve parameters with different physical aspects and different International System units. They are only used to calculate values. The third degree polynomial equations that best describe the temperature evolution using frequency, power and scanning velocity separately are given below.



As can be seen in Equations (16), (17), and (18), the coefficients are much higher when comparing the scanning velocity and the frequency (


Figure 9. Predicted case depth versus Measured case depth.
predicted case depth versus measured case depth. This line has a linear equation that can be written as follows:

5. Conclusion
The mechanical attributes of the hardened surface achieved by induction heating process are influenced by physical and chemical properties of the treated material and several induction heating parameters and conditions. To be able to use correctly the resources offered in this process, it is necessary to develop a comprehensive strategy to control the heating parameters in order to produce the desired hardened surface characteristics for a specific application. Current practices in the industry are based on the control of the induction heating process using the traditional and fastidious trial and error procedures for every single specific part. Based on correlation analysis between various induction heating parameters and final hardness profile developed in the case of stationary induction heating, this paper presents an investigation of non-stationary heating process. The approach proposed in this study focuses on the effects of power, frequency variation and especially scanning speed analysis through extensive 3D modelling and simulation, structured experimental efforts and improved statistical analysis tools. Based on coupled electromagnetic and thermal fields analysis, the developed 3D model is used to estimate the temperature distribution as well as the hardness profile attributes. ANOVA is used to evaluate the contribution of each parameter in temperature and hardness profile attributes variations. Experimentations conducted on a commercial dual-frequency induction machine for AISI 4340 steel splines confirm the feasibility and the validity of the proposed approach. The validation results reveal a great concordance between simulated and measured profiles and confirm that the model can effectively be used as simulation framework for understanding the process and for assessing the effects of various parameters on the hardening process quality and performance leading consequently to the most relevant variables to use in an eventual hardness profile prediction model.
Cite this paper
Hammi, H., El Ouafi, A., Barka, N. and Chebak, A. (2017) Scanning Based Induction Heating for AISI 4340 Steel Spline Shafts-3D Simulation and Experimental Validation. Advances in Ma- terials Physics and Chemistry, 7, 263-276. https://doi.org/10.4236/ampc.2017.76021
References
- 1. Jomaa, W., Songmene, V. and Bocher, P. (2013) On Residual Stress Changes after Orthogonal Machining of Induction Hardened AISI 4340 Steel. Proceedings of Materials Science and Technology Conference and Exhibition, MS&T 13, 94-103.
- 2. Grum, J. (2000) Measuring and Analysis of Residual Stresses after Induction Hardening and Grinding. Materials Science Forum, 347, 453-458.
https://doi.org/10.4028/www.scientific.net/MSF.347-349.453 - 3. Hammi, H., Barka, N. and El Ouafi, A. (2015) Effects of Induction Heating Process Parameters on Hardness Profile of 4340 Steel Bearing Shoulder Using 2D Axisymmetric Model. International Journal of Engineering and Innovative Technology, 4, 41-48.
- 4. Hammi, H., El Ouafi, A. and Barka, N. (2016) Study of Frequency Effects on Hardness Profile of Spline Shaft Heat-Treated by Induction. Journal of Materials Science and Chemical Engineering, 4, 1-9.
https://doi.org/10.4236/msce.2016.43001 - 5. Sadeghipour, K., Dopkin, J.A. and Li, K. (1996) A Computer Aided Finite Element/ Experimental Analysis of In-duction Heating Process of Steel. Computers in Industry, 28, 195-205.
https://doi.org/10.1016/0166-3615(95)00072-0 - 6. Boadi, A., Tsuchida, Y., Todaka, T. and Enokizono, M. (2005) Designing of Suitable Construction of High-Frequency Induction Heating Coil by Using Finite-Element Method. IEEE Transactions on Magnetics, 41, 4048-4050.
https://doi.org/10.1109/TMAG.2005.854993 - 7. Zabett, A. and Mohamadi Azghandi, S.H. (2012) Simulation of Induction Tempering Process of Carbon Steel Using Finite Element Method. Materials & Design, 36, 415-420.
https://doi.org/10.1016/j.matdes.2011.10.052 - 8. Magnabosco, I., Ferro, P., Tiziani, A. and Bonollo, F. (2006) Induction Heat Treatment of a ISO C45 Steel Bar: Experimental and Numerical Analysis. Computational Materials Science, 35, 98-106.
https://doi.org/10.1016/j.commatsci.2005.03.010 - 9. Di Luozzo, N., Fontana, M. and Arcondo, B. (2012) Modelling of Induction Heating of Carbon Steel Tubes: Mathematical Analysis, Numerical Simulation and Validation. Journal of Alloys and Compounds, 536, S564-S568.
https://doi.org/10.1016/j.jallcom.2011.12.084 - 10. Barka, N., El Ouafi, A.E., Chebak, A., Bocher, P. and Brousseau, J. (2012) Study of Induction Heating Process Applied to Internal Gear Using 3D Model. Applied Mechanics and Materials, 232, 730-735.
https://doi.org/10.4028/www.scientific.net/AMM.232.730 - 11. Savaria, V., Bridier, F. and Bocher, P. (2012) Computational Quantification and Correction of the Errors Induced by Layer Removal for Subsurface Residual Stress Measurements. International Journal of Mechanical Sciences, 64, 184-195.
https://doi.org/10.1016/j.ijmecsci.2012.07.003 - 12. Favennec, Y., Labbé, V. and Bay, F. (2003) Induction Heating Processes Optimization a General Optimal Control Approach. Journal of Computational Physics, 187, 68-94.
https://doi.org/10.1016/S0021-9991(03)00081-0 - 13. Naar, R. and Bay, F. (2013) Numerical Optimisation for Induction Heat Treatment Processes. Applied Mathematical Modelling, 37, 2074-2085.
https://doi.org/10.1016/j.apm.2012.04.058