Advances in Materials Physics and Chemistry
Vol.04 No.12(2014), Article ID:52354,8 pages
10.4236/ampc.2014.412030
Minimum Amount of Extracting Solvent of a Separation of Two Rare Earth Components
Fuxiang Cheng1, Sheng Wu1,2, Yan Liu1, Songling Wang1, Bo Zhang1, Chunsheng Liao1,2*, Chunhua Yan2
1China Minmetals (Beijing) Research Institute of RE Co., Ltd., Beijing, China
2Beijing National Laboratory for Molecular Sciences, State Key Laboratory of Rare Earth Materials Chemistry and Applications, PKU-HKU Joint Lab on Rare Earth Materials and Bioinorganic Chemistry, Peking University, Beijing, China
Email: *cfx@cre-ol.com
Academic Editor: Kun Huang, Institute of Process Engineering, Chinese Academy of Sciences, China
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 October 2014; revised 26 November 2014; accepted 9 December 2014
ABSTRACT
A significant development in the theory of countercurrent extraction will be presented in this article. New expressions of the term in countercurrent extraction process analysis, “Adjacent Stage Impurity Ratio” (ASIR), are deduced. Furthermore, based on the term together with mass balance and extraction equilibrium, the conditions where a given countercurrent extraction separation operation can have minimum amounts of both extracting solvent and scrubbing agent solution can be estimated, and the equations of the two minimum amounts can be deduced. It was found that the equations for a two-component separation using a single aqueous or organic feed are exactly the same as they appeared in the theory initially established in 1970s. Unlike its earlier version, the present derivation does not involve feed-stage-composition hypothesis, and also has the advantage of dealing with a double-feed system where both aqueous and organic feeds are simultaneously employed whereas the earlier theory can only analyze a separation using a single aqueous or organic feed.
Keywords:
Theory of Countercurrent Extraction, Minimum Amount of Extracting Solvent, Two-Component Separation, Adjacent Stage Impurity Ratio

1. Introduction
The theory of countercurrent extraction was primarily established in 1970s [1] - [5] . The theory was initially applied to the design of extraction separation processes of rare earths (REs), and contributed a lot to the rapid development of RE separation industry in China [6] - [13] . The design of a given separation process, including estimating the number of ideal stages, amounts of both extracting solvent and scrubbing agent solution, and product purity, etc., has become more readily performed after advanced modeling techniques were developed [14] [15] .
In recent years, a major focus of separation technology development has been to consume less chemical and to discharge less pollution during production [16] - [19] . Therefore it is necessary to clearly know the minimum amount of extracting solvent (denoted hereafter as Smin) and the minimum amount of scrubbing agent solution (denoted hereafter as Wmin) which represents the limit of chemical consumption for a given separation.
The equations of Smin and Wmin for a two-component separation using a single aqueous or organic feed were previously given in the theory of countercurrent extraction based on several hypotheses [3] [5] . One of the hypotheses, the feed-stage-composition hypothesis, presupposes that the same kind of phase as the feed also has the same solute composition as the feed when it flows out of the feed stage. Recently however, we found this hypothesis to be not necessary. In this article, we presented different expressions of the term of Adjacent Stage Impurity Ratio from before [20] , and then in the absence of feed-stage-composition hypothesis, we derived the equations of Smin and Wmin which are found to have the same forms as they previously appeared for a two-com- ponent separation using a single feed. Of more significance, we obtained the equations of Smin and Wmin for a separation using both aqueous and organic feed simultaneously, i.e., using double feeds which may be encountered in a hyperlink process of multi-component separation, for the first time. Therefore the present work will support the design of hyperlink extraction processes together with our previous articles [21] [22] .
2. Description of the Separation System
The present article is focused on the counter current extraction separation processes of a mixture with two components, as displayed in Figure 1. A and B refer to two kinds of metal ions with the same valency, with A is the more extractable ion than B in the given extraction system. Their separation factor is denoted as β.
The whole separation cascade couples n extraction stages and m scrubbing stages. The barren saponified solvent and hydrochloric acid enter 1st stage and (n + m)th stage respectively as extracting solvent and scrubbing agent solution. Here for brevity the term “extracting solvent” is used to include solvent mixtures. A single aqueous feed enters the cascade from nth stage with feed flowrates (hereafter in mole per unit time) of A and B of fA,a and fB,a respectively, and a single organic feed is led into (n + 1)th stage of the cascade with feed flowrates of A and B of fA,o, fB,o respectively all the time. The final raffinate carrying all the pure B leaves the cascade at 1st stage, while the organic stream containing the pure A flows out of the cascade from (n + m)th stage as the final extract.
It is assumed that the extracting solvent and the aqueous solution are immiscible and remain so at all cases of the operation. It is assumed that each stage is an equilibrium stage, and therefore all the flowrates are out of each stage in equilibrium. It is also assumed that only the saponified extractant has the ability of extraction with a single cation-exchange mechanism. The saponified extracting solvent is supposed to be always saturated with components when leaving all stages except (n + m)th stage. All the H+ ion in the starting scrubbing acid is supposed to immediately exchange and migrate towards organic phase after entering the cascade, and therefore the scrubbing agent solution has contained no acid since leaving (n + m)th stage. And also as the two components have the same valency, the mixed extraction factor, denoting the ratio of the total mole amount of the two
Figure 1. Cascade diagram for countercurrent extraction separation of two components.
components in the organic phase to that in the aqueous phase, will keep constant either through extraction stages except stage 1 or through scrubbing stages except stage (n + m). Accordingly the flowrate of extracting solvent, represented by S, should be equal to the total organic flowrate of two components leaving all the extraction stages, and that of scrubbing agent solution, denoted by W, should correspond to the total aqueous flowrate leaving all the scrubbing stages.
3. Expressions of Adjacent Stage Impurity Ratio
According to the target of A/B separation, a raffinate with pure component B should be obtained in the aqueous exit located in 1st stage, thus component A can be regarded as the impurity to be gradually withdrawn from the aqueous phase by extracting solvent through extraction stages. In order to intuitively describe the removal efficiency of the impurity A in a certain extracting stage, we introduce a term named as Adjacent Stage Impurity Ratio (abbreviated as ASIR) in kth extraction stage as Equation (1) where g represents the ASIR and xi,k (i = A or B) represent the aqueous flowrates of the two components respectively when leaving stage k, and so on.
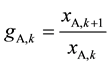 (1)
(1)
On the contrary, an extract with pure A should be obtained from (n + m)th stage, and component B is the impurity to be removed stage by stage from the organic stream through the scrubbing section. ASIR in kth scrubbing stage can then be expressed as in Equation (2) where yi,k (i = A or B) represent the organic flowrates of the two components respectively when leaving stage k, and so on.
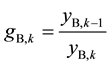 (2)
(2)
In Figure 2, xi,k and yi,k (i = A or B) again represent the aqueous and organic flowrates of the two components respectively when leaving stage k, and so on. According to mass balance as well as extraction equilibrium, we can have the following relations in Equations (3)-(5), in which k refers to an extraction stage and S means the total organic flowrates of A and B leaving any extraction stage.
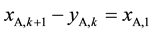 (3)
(3)
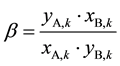 (4)
(4)
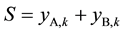 (5)
(5)
From Equations (4) and (5), we know that
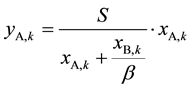 (6)
(6)
Then introducing Equation (6) into Equation (3) and taking Equation (1) into account, ASIR of kth extraction stage can be expressed as:
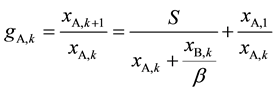 (7)
(7)
Figure 2. Schematic diagram of flow in 3 continuous extraction or scrubbing stages (i = A or B).
If the same analysis as above is applied to the scrubbing section, ASIR of kth scrubbing stage can be derived as Equation (8).
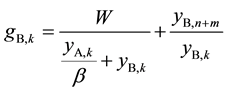 (8)
(8)
In the extraction section, each organic stream out of a stage will contact in the next stage an aqueous stream containing no less component A than that in equilibrium with it, and therefore during each new contact, there should be some amount of component A entering the organic phase, along with equivalent component B ex-
changed into the aqueous phase, as a result of which 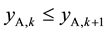 and
and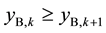 . Also because
. Also because 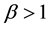 and
and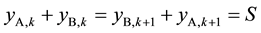 , it can be known from Equation (7) that
, it can be known from Equation (7) that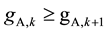 . Similarly
. Similarly 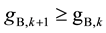
in scrubbing section. Therefore ASIR shows monotonous increase trends from the central feed stage towards two ends, which is the basis of deducing the equations of Smin and Wmin in the next section.
4. Equations of Smin and Wmin
ASIR gives an intuitive view of the removal status of an impurity in a separation cascade. The process of impurity removal is caused by a concentration driving force. When there is no concentration driving force, extracting solvent or scrubbing agent solution will lose the power to withdraw the impurity from its opposite liquid phase contacting with it, and the value of ASIR will drop to 1. As mentioned earlier, A/B separation requires the attainment of a final raffinate with no A as well as a final extract with no B, so if an S lower than the minimum value needed (Smin) is used in a separation cascade with enough stages, such that the compositions of the two outlets will not change when one or more stages are added, the two following events will happen: 1) ASIR at some continuous extraction stages adjacent to feed stage drops to 1, and 2) excess impurity A will exist in the final raffinate. However, if S is gradually increased, the final raffinate will contain less and less A. Therefore Smin should correspond to the flowrate of extracting solvent resulting that the content of impurity A in the final raffinate just reaches the requirement while the lowest value of ASIR in extraction section keeps 1, which is the basic principle to derive the equation of Smin. Actually, the principle also applies to the derivation of Wmin. And because ASIR monotonously increases from feed stage towards the two opposite ends of a cascade, the equations of both Smin and Wmin will be derived on the conditions that the purities of both raffinate and extract are just up to the required level and ASIR of some continuous stages including the feed stage located in the middle has a same value of 1.
4.1. A Single Aqueous Feed
As usual consideration, the stage receiving an aqueous feed is regarded as an extraction stage, thus the aqueous feed is supposed to enter the cascade from nth stage as displayed in Figure 1. If

The separation goal requires no A existing in final raffinate, therefore

From Equations (9) and (10), an interesting conclusion can be addressed as Equation (11) which reveals that the aqueous and organic flowrates of impurity leaving a same extraction stage should be equal to each other if ASIR of this stage is 1.

Similarly if

Then the equation of extraction equilibrium in stage n can be simplified as:

Meanwhile the balance of component B across the interface I in Figure 3 should be:

Connecting Equation (13) with Equation (14), we can have


Equation (15) gives the allowed minimum flowrate of component B from the feed stage with the aqueous stream in order to attain the exiting aqueous flowrate up to fB,a.
Then we analyze the scrubbing section with the aim of acquiring the flowrates of component A in the stages with ASIR of 1. When both 


and then the simplified extraction equilibrium equation of stage (n + 1) as below:

Also in scrubbing section, 


The flowrates of component A with aqueous and organic streams flowing out of stage (n + 1) can be deduced as follows.


After the separate analysis on either extraction or scrubbing section, we consider the mass balance of both A and B across the interface II in Figure 3, and then we know:


Figure 3. Materials in the area near feed stage (aqueous feed at nth stage and organic feed at [n + 1]th stage).
From Equations (12), (20), and (22), the aqueous and organic flowrates of component A leaving the feed stage, i.e. stage n, can be expressed as below.

Meanwhile from Equations (16), (17), and (23), we can also obtain the expressions of the aqueous and organic flowrates of component B leaving stage (n + 1) as Equation (25).

So far, we have derived all the flowrates of two components leaving two adjacent stages with ASIR of 1, stage n in extraction section and stage (n + 1) in scrubbing section. As discussed above, Smin and Wmin should correspond to the condition that ASIRs of both stage n and stage (n + 1) have the value of 1, therefore:


Because 



Both of Equations (28) and (29) have the identical forms as appeared in the earlier theory of countercurrent extraction. Additionally, from Equation (24) and (15), it is obvious that the aqueous stream leaving stage n, i.e., the feed stage, has the same solute composition as the initial aqueous feed, which supports the feed-stage-com- position hypothesis proposed in the theory of countercurrent extraction earlier.
4.2. A Single Organic Feed
Differently from using an aqueous feed, the feed stage is considered as a scrubbing stage when it receives an organic feed. Based on the similar analysis using a single aqueous feed above, it is found that the equations from (9) to (21) are also suitable for the case using a single organic feed, but with fA,a and fB,a changed to fA,o and fB,o respectively. Thus we derive the aqueous and organic flowrates of component B leaving stage n as below:


as well as the aqueous and organic flowrates of component A leaving stage (n + 1) as follows:


Also differently from those using a single aqueous feed, mass balance relations of the two components across the interface II are found to have the forms as shown in Equations (34) and (35).


Then from Equations (12), (32), and (34), we have

and from Equations (17), (31), and (35), we have

Finally introducing Equations (30) and (36) into Equation (26), and Equations (33) and (37) into Equation (27), one can obtain the expressions of minimum amounts of extracting solvent and scrubbing agent solution for a two-component separation with a single organic feed as below:


Equations (38) and (39) also have good agreement with the earlier theory. Meanwhile it is found from Equations (33) and (37) that the solute composition of the organic stream leaving stage (n+1), i.e., the feed stage, is exactly the same as that of the starting organic feed.
4.3. Double Feeds
Hyperlink extraction technology, due to its striking advantage of decreasing the use of chemicals for multi- component separation, has been extensively employed in the Chinese rare earth separation industry [19] . In hy- perlink processes, it is possible for a sublevel separation to accept both the aqueous phase and the organic phase respectively from two adjacent higher separation levels as its double feeds. The earlier theory of countercurrent extraction did not give the equations of Smin and Wmin for a double-feeding separation. In a double-feeding separation, the aqueous feed enters nth stage which is an extraction stage, and the organic feed flows into the cascade at stage (n + 1) which is considered as a scrubbing stage. Same as above, when both Smin and Wmin are given to the double-feeding separation, ASIR of stage n as well as that of stage (n + 1) should be equal to 1, which requires the relative flowrates to still satisfy the equations from (9) to (13), (17) and (18). However the mass balance of component B across the interface I will change to:

Then simultaneously considering Equations (13) and (40), we find:


The mass balance of component A across the interface III changes to:

Thus from Equations (18) and (43), the aqueous and organic flowrates of component A leaving stage (n+1) can be expressed as Equations (44) and (45) respectively.


The mass balance of the two components across the interface II can be represented by Equations (46) and (47).


Then from Equations (12), (44), and (46), one can drive Equation (48):

and from Equations (17), (42), and (47), the relation described in Equation (49) can be obtained.

Finally Smin can be obtained by simultaneously taking Equations (26), (42), and (48) into account, and Wmin by connecting Equations (27), (45), together with Equation (49), as follows:


By comparing Equations (50) and (51) with Equations (28), (29), (38), and (39), we can address an important conclusion that Smin required for a double-feeding separation equals the sum of the minimum amounts of extracting solvent demanded when independently separating the two feeds. Also from Equations (41) and (48), Equations (45) and (49), it can be found that these flowrates no longer satisfy the feed-stage-composition hypothesis, which is the reason that the earlier theory of countercurrent extraction is incapable of dealing with a double-feeding separation.
5. Conclusion
The earlier theory of countercurrent extraction gave the equations of minimum amounts of extracting solvent and scrubbing agent solution for a two-component separation using a single aqueous or organic feed on the basis of some hypotheses including feed-stage composition hypothesis. The present study reveals that those equations also can be deduced without using of the feed-stage-composition hypothesis with the aid of the ASIR concept. The feed-stage-composition hypothesis can be proven to be correct in the case of using a single aqueous or organic feed, but invalid when double feeds are used. Of great significance is to present an approach in this work that can deal with a double-feeding separation, a problem that has not been solved before. The result suggests that the use of a second organic feed will not change the minimum amounts of extracting solvent and scrubbing agent solution demanded for an aqueous feed, and vice versa.
Acknowledgements
This research was supported by the National Basic Research Program of China (973) (2012CBA01200).
References
- Xu, G.X. (1978) Theory of Counter Current Extraction I. Equations of Optimization and Their Applications. Acta Scientiarum Naturalium Universitatis Pekinensis, 1, 51-66. (In Chinese)
- Li, B.G., Xu, X.Y. and Xu, G.X. (1980) Theory of Counter Current Extraction III: A Mathematical Model for the Dynamic Equilibrium of Counter Current Extraction. Acta Scientiarum Naturalium Universitatis Pekinensis, 1, 66-84. (In Chinese)
- Xu, G.X., Li, B.G. and Yian, C.H. (1985) Theory of Countercurrent Extraction and Its Applications in Rare Earth Extraction Industry. In: New Frontiers in Rare Earth Science and Applications, Science Press, Beijing, 429-437.
- Li, B.G., Li, J.R., Yian, C.H., Qiao, S.P. and Xu, G.X. (1985) Theory of Countercurrent Extraction VII. Dynamic Equilibrium in Three-Component System. In: New Frontiers in Rare Earth Science and Applications, Science Press, Beijing, 438-441.
- Xu, G.X. (2005) Theory of Countercurrent Extraction. In: Rare Earths, Metallurgical Industry Press, Beijing, 612-727. (In Chinese)
- Yan, C.H. (1988) One-Step Scale-Up of Rare Earth Extraction Separation Process. Doctoral Dissertation, Peking University, Beijing. (In Chinese)
- Gao, S. (1988) Theory and Industrial Applications of Five-Component Countercurrent Extraction System. Doctoral Dissertation, Peking University, Beijing. (In Chinese)
- Xu, G.X., Gao, S., Li, B.G., Yan, C.H. and Huang, C.H. (1993) New Progresses on Extraction Separation Processes of Rare Earths. Journal of the Chinese Rare Earth Society, 11, 193-198. (In Chinese)
- Wang, Z.H. (1995) Design Calculation for Multi-Component Rare Earth Separation by Solvent Extraction: Equivalent Composition-Equivalent Separation Factor Method. Chinese Rare Earths, 16, 10-14. (In Chinese)
- Liao, C.S. (1996) Extraction Separation of Heavy Rare Earths. Doctoral Dissertation, Peking University, Beijing. (In Chinese)
- Huang, X.W., Long, Z.Q., Li, H.W., Ying, W.W., Zhang, G.C. and Xue, X.X. (2005) Development of Rare Earth Hydrometallurgy Technology in China. Journal of Rare Earths, 23, 1-4.
- Han, Q.Y., Yang, J.H., Li, J.F. and Bai, W. (2011) New Three-Group Progress for Separation of the Rare Earth Mineral with Middle Y and Rich Eu. Chinese Rare Earths, 32, 72-77. (In Chinese)
- Hao, J.N., Zhang, L.P., Yian, C.H., Li, B.G. and Xu, G.X. (1985) Experimental Verification of Countercurrent Extraction Theory Separation of La and Ce by HEH(EHP) in New Frontiers in Rare Earth Science and Applications. Science Press, Beijing, 442-445.
- Wu, S., Liao, C.S., Jia, J.T. and Yan, C.H. (2004) Static Design for Multiple Components and Multiple Outlets Rare Earth Countercurrent Extraction [I]: Algorithm of Static Design. Journal of the Chinese Rare Earth Society, 22, 17-21. (In Chinese)
- Wu, S., Liao, C.S., Jia, J.T. and Yan, C.H. (2004) Static Design for Multi-Component and Multi-Outlet Rare Earth Countercurrent Extraction [II]: Static Design and Its Verification. Journal of the Chinese Rare Earth Society, 22, 171- 176. (In Chinese)
- Yan, C.H., Jia, J.T., Liao, C.S., Wu, S. and Xu, G.X. (2006) Rare Earth Separation in China. Tsinghua Science and Technology, 11, 241-247. http://dx.doi.org/10.1016/S1007-0214(06)70183-3
- Feng, Z.Y., Huang, X.W., Liu, H.J., Wang, M., Long, Z.Q., Yu, Y. and Wang, C.M. (2012) Study on Preparation and Application of Novel Saponification Agent for Organic Phase of Rare Earths Extraction. Journal of Rare Earths, 30, 903-908. http://dx.doi.org/10.1016/S1002-0721(12)60152-5
- Han, Q.Y. (2013) Technical and Economical Evaluation on Separation of Light Rare Earth. Journal of the Chinese Rare Earth Society, 31, 399-404. (In Chinese)
- Liao, C.S., Wu, S., Cheng, F.X., Wang, S.L., Liu, Y., Zhang, B. and Yan, C.H. (2013) Clean Separation Technologies of Rare Earth Resources in China. Journal of Rare Earths, 31, 331-336. http://dx.doi.org/10.1016/S1002-0721(12)60281-6
- Cheng, F.X., Wu, S., Liao, C.S. and Yan, C.H. (2013) Adjacent Stage Impurity Ratio in Rare Earth Countercurrent Extraction Process. Journal of Rare Earths, 31, 169-173. http://dx.doi.org/10.1016/S1002-0721(12)60253-1
- Cheng, F.X., Wu, S., Liu, Y., Wang, S.L., Zhang, B., Liao, C.S. and Yan, C.H. (2014) Minimum Amount of Extracting Solvent for AB/BC Countercurrent Separation Using Aqueous Feed. Separation and Purification Technology, 131, 8- 13. http://dx.doi.org/10.1016/j.seppur.2014.04.031
- Cheng, F.X., Wu, S., Zhang, B., Liu, Y., Wang, S.L., Liao, C.S. and Yan, C.H. (2014) Minimum Amount of Extracting Solvent of AB/BC Countercurrent Extraction Separation Using Organic Feed. Journal of Rare Earths, 32, 439-444. http://dx.doi.org/10.1016/S1002-0721(14)60091-0
NOTES
*Corresponding author.





