Advances in Materials Physics and Chemistry
Vol.2 No.4(2012), Article ID:25999,7 pages DOI:10.4236/ampc.2012.24033
Theoretical Study of Dibenzothiophene Based Electron Transport Materials
Applied Materials Sciences Group, Pacific Northwest National Laboratory, Richland, USA
Email: asanga.padmaperuma@pnl.gov
Received August 3, 2012; revised September 3, 2012; accepted September 12, 2012
Keywords: OLED; Electron Transport Molecules; PO15; Dibenzothiophene; DFT; TD-DFT
ABSTRACT
Density functional methods have been used for the calculation of electronic structures, electronic transitions, vertical electron affinities and intermolecular reorganization energies for tri-aryl substituted dibenzothiophenes. These model compounds were then compared to the predicted values for dibenzo[b,d]thiophen-2-yltriphenylsilane (DBTSI 2) and to dibenzo[b,d]thiophene-2,8-diylbis(diphenylphosphine oxide) (PO15), known electron transport molecules. The results indicate that these model compounds can be used in a blue OLED system.
1. Introduction
Numerous advances in organic light emitting device (OLED) technology have occurred since the discovery by Tang and van Slyke [1]. This is due in part to the synthetic versatility of organic materials, which can be designed with tuned properties, including emission energy, charge transport, and morphological stability, all important for efficient OLED operation. As a result, displays based on this technology have become available in the marketplace. A further outcome of this progress is that the efficiency of OLEDs has increased to the point where they are within range of solid state lighting (white light) applications. Realizing this potential has created new challenges to overcome. Blue electrophosphorescence, which is a necessary component of white light, has been a particular challenge because the triplet excited state of the material system (host, hole transport and electron transport materials) must be higher than that of the dopant in order to prevent quenching of the dopant emission (see Figure 1) [2]. This requires a host material with even higher triplet energy than the blue phosphor dopant. Consequently, reports of high efficiency and long-lived blue phosphorescent OLEDs have been rare, in part because of the lack of appropriate organic charge transport materials into which to dope the phosphorescent emitter.
The most important factor to optimize the external quantum efficiency of an OLED is the charge balance in the emissive layer [3]. The charge balance depends on injection of carriers at the electrodes as well as balanced charge mobility by the transport layers. Unlike many other parameters that govern OLED performance, this needs to be addressed at the design stage of the molecules. This, in turn, means that one needs to look for materials which possess desirable ionization potentials and electron affinities at the electron and hole injecting interface in order to get efficient charge injection.
Also, the molecule must possess the inherent ability to transport the desired charge carrier. In order to ensure that a molecule has favorable performance in an OLED, many factors (chemical and physical) need to be optimized. This means parameters such as ion stability, relaxation energies, luminescence yields and molecular orbital energy levels must be known. Theoretical methods can be used to evaluate some of these potential targets [4]. Here, we use density functional theory to evaluate a class of molecules as potential candidates for the electron transport layer (ETL). These model compounds are then compared to a state of the art material (PO15) we have reported [5]. The model ETL we study here are based on a dibenzothiophine moiety attached to one or two triphenylsilane groups (Figure 2).
2. Theoretical Methods
All calculations were performed with the NWChem computational package [6], at the Molecular Science Computing Facility (MSCF) in the Environmental Molecular Sciences Laboratory (EMSL). Molecular orbitals and bond lengths were visualized using Extensible Computational Chemistry Environment (ECCE) a component of the Molecular Science Software Suite (MS3) developed at the Pacific Northwest National Laboratory (PNNL) [7]. Geometry optimization and electronic properties
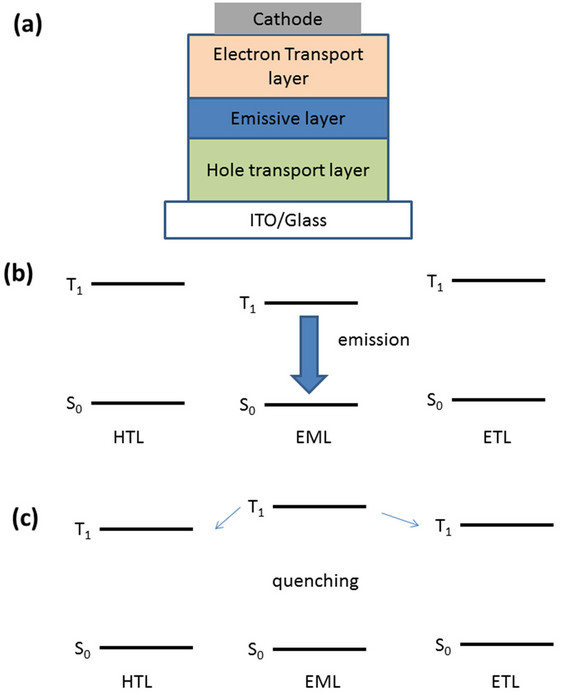
Figure 1. (a) Schematic representation of an simple OLED; (b), (c) The relationship of the relative triplet energies of ETL, HTL and the emitter.

Figure 2. Chemical structures of the molecules studied.
were computed at the density functional theory (DFT) level. For the DFT calculations, B3LYP hybrid functionals were employed [8]. It is common these days to use a high level basis set for these kind of electronic property calculations.
Here, we used Pople’s standard split-valence plus polarization 6-31G*, [9] and Dunning’s correlation consistent (double zeta) basis set cc-pVDz basis set [9] to optimize the geometry of DBTSI 2. These predicted values were then compared to the experimental values obtained by our group previously [10] (Tables 1 and 2). The element numbers are shown in Figure 3. Although Dunning’s correlation consistent basis sets have had redundant functions removed and have been rotated in order to increase computational efficiency [11-17], the computer time needed for 6-31G* calculations are still shorter.
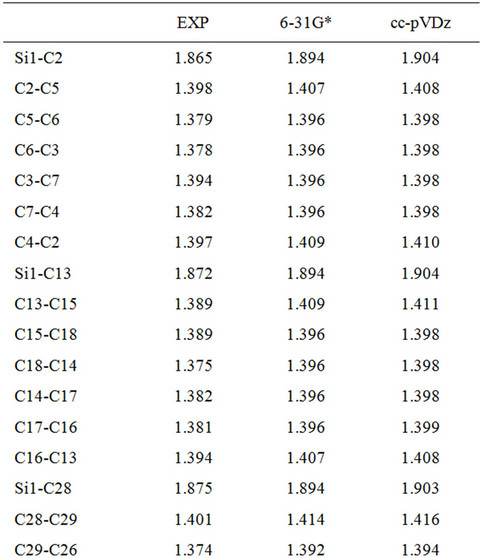
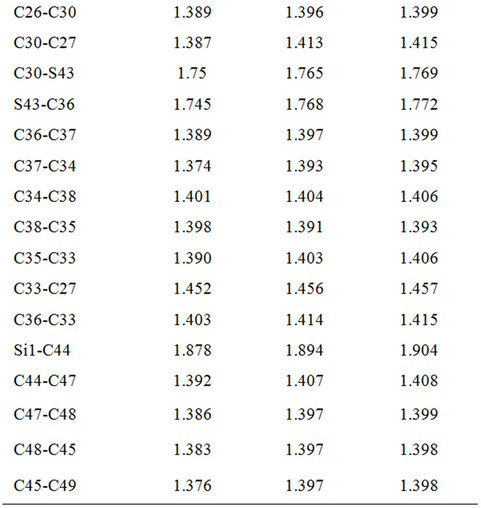
Table 1. Bond lengths predicted for DBTSI2.
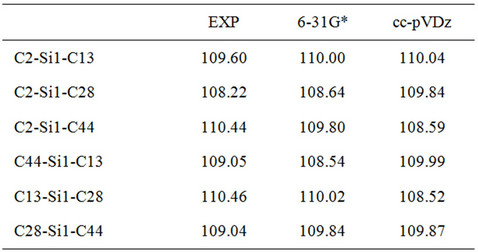
Table 2. Bond angles predicted for DBTSI2.
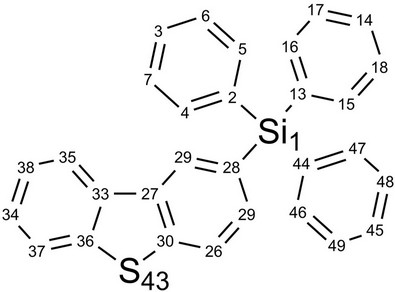
Figure 3. The element numbers for DBTSI 2.
From the data it is clear that the higher level of basis set does not provide an accurate description of the geometry. As such, for the geometry optimization Pople’s standard split-valence plus polarization 6-31G* basis set was used.
In previous work, we studied several classes of electronic molecules using different DFT type functionals and 6-31G* as the basis set. From this work we established that the B3LYP/6-31G* level of theory gave values that closely matched the experimental values for bond lengths, bond angles and orbital energies [18]. The highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) energies were determined from the minimized singlet geometry (Table 3). Electron binding energies and ionization potentials of molecules were calculated by the delta self-consistent field (ΔSCF) as the difference in energy between a molecule and its radical cation. The same level of theory was applied to both the anion and the neutral species for the electron affinity calculations. The spin unrestricted B3LYP (UB3LYP) density functional was employed to treat the species with an ionized open-shell doublet (one unpaired electron) electron configurations. The results obtained with theΔSCF method were compared with calculations based on the traditional Koopmans’ theorem approach [19]. The DFT was used to investigate the effects of substitution on the reorganization energy. The total reorganization energy was evaluated based on
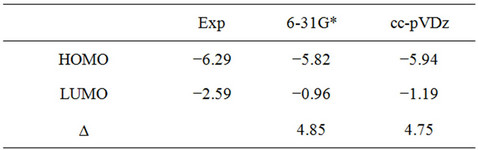
Table 3. Orbital energies predicted for DBTSI2.
adiabatic potential energy surfaces (AP) model according to work published by Brédas [20].
3. Results and Discussion
3.1. Molecular Orbitals
The π-molecular orbitals for the highest occupied and the lowest unoccupied orbital of dibenzothiophene (DBT) is shown in Figure 4. In the case of the occupied MO, there is π-electron density on the sulfur atom. There are two nodes on this MO in addition to those on the C3 and the C7 positions. When the LUMO is considered, there are nodes on the sulfur atom, as well as the C2 and the C8 positions. The effect of Ph3Si-substitution on the energy of the HOMO and LUMO levels of DBT was studied next (Figure 5). The substitution on the C1, C3 and C4 destabilized the HOMO level of DBT by 0.1 eV, 0.03 eV, and 0.10 eV respectively. Substitution on the C2 had no effect on the HOMO level, the same was seen for disubstitution at C2and C8 (short axis). However, di-substitution on C3and C7 (long axis) of DBT destabilized the HOMO by 0.05 eV. The LUMO level was stabilized by substitution except for on the C4 position. The substitution on the C1, C2 and C3 stabilized the LUMO level of DBT by 0.11 eV, 0.02 eV, and 0.14 eV respectively. Also, di-substitution on C2and C8 (short axis) and on C3and C7 (long axis) stabilized the LUMO level of DBT by 0.03 eV, 0.28 eV respectively.
3.2. HOMO-LUMO Gap and Lowest Excitation Energies
The energy gap between the occupied and the unoccupied levels can be theoretically predicted using two methods. The first method is based on ground state calculations, from which the band gap is estimated as the energy difference between the HOMO and the LUMO (ΔH-L) [21-23]. The second method is the use of time dependent density functional theory (TD-DFT). TD-DFT methods can be used to study complex systems due to their relatively low computational cost, and the ability to include in its formalism the electron correlation effects. The HOMO-LUMO gaps (ΔH-L) and lowest singlet excited energies (S1) are both listed in Table 4. The S1 state is always due to the HOMO-LUMO transition. The dominant transition is localized on the DBT moiety for all the molecules. This is in accordance with what we
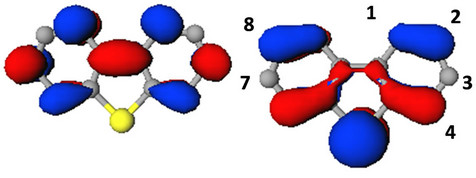
Figure 4. The LUMO (top) and the HOMO (bottom) state of dibenzothiophene.
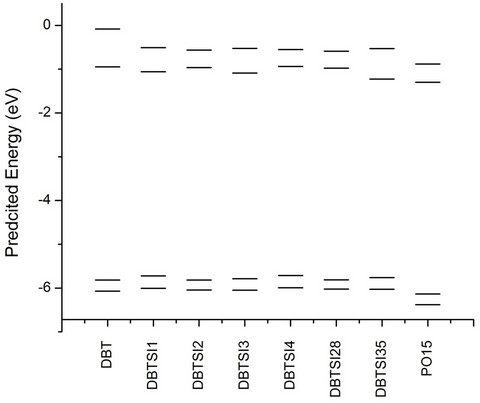
Figure 5. The predicted energy levels of the substituted silanes.
observed for this type of structures before [10]. As expected, the substitution of the DBT core lowers the bandgap. However, these molecules still maintain the necessary values to be used as ETLs for a blue OLED system.
3.3. Ionization Potentials, Electron Affinities, and Triplet Energy
It is important to design host molecules with efficient injection and transport of both holes and electrons. These are also important parameters that need to be optimized during the rational design of molecules for optimized OLEDs.
Ionization potentials (IP) and electron affinities (EA) are used to estimate the energy barrier for the injection of both holes and electrons into the molecule in question. The arylsilane substitution reduces the IP for the DBT moiety, and the substitution has different effects on the EA. As mentioned, the triplet energy (ET) of these molecules needs to be higher than that of the emitter. The ETL material PO15 has shown that it has a suitable ET, and is used as the baseline for this study. The lowest energy singlet-triplet transition energy was calculated using TD-DFT methods (Table 4). The triplet energy was also calculated according to methods published by Brédas (Table 5) [24]. All molecules studied here do have an ET similar to the baseline molecule PO15 and have the potential to be used as ETLs for a blue OLED system.
3.4. Reorganization Energy
The electron transport properties can be explained using the semi-classical Marcus theory [25] or the BixonJortner model [26]. Either way, it is clear that the reorganization energy plays an important role when it comes to controlling the electron transfer rates. The reorganization energy includes contributions from the in tramolecular and intermolecular energy change during a charge transfer


Table 4. Electronic transition data.
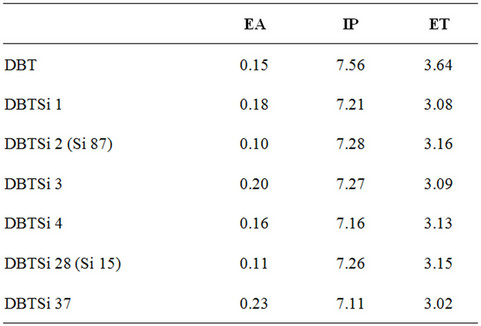
Table 5. Electron affinities, ionization potentials, and triplet energies for each molecule (in eV).
event. The intramolecular reorganization energy refers to the relaxation of the molecule involved in the charge transfer process. The intermolecular reorganization energy refers to the relaxation of the medium in which the charge transfer takes place. First-principle quantum chemistry calculations can be performed to investigate the charge transport properties. In this study we have focused on estimating the intramolecular reorganization energy (λ) to evaluate the molecules studied. The adiabatic potential energy surfaces method, as outlined in Figure 6 was used in the calculation of reorganization energy.
For the neutral molecule A, the reorganization energies for hole transport and electron transport are as follows:

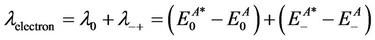
In these equations; 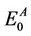 and
and 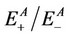 are the energies of neutral and cation/anion molecules in the optimized geometries. The
are the energies of neutral and cation/anion molecules in the optimized geometries. The 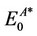 and
and 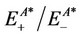 are the energies of neutral and cation/anion monomers with the cation/anion and neutral geometries, respectively. The data calculated for the substituted silanes is shown in Table 6.
are the energies of neutral and cation/anion monomers with the cation/anion and neutral geometries, respectively. The data calculated for the substituted silanes is shown in Table 6.
We have demonstrated previously that lower reorganization energy corresponds to a higher charge transport rate [27]. Based on this knowledge we can rank the molecules in the series. Substitution on the C2 position results in highest electron transport rate. For mono-substituted molecules the rate of electron transport is DBTSI 2 > DBTSI 4 > DBTSI 1 > DBTSI 3. For mono-substituted molecules the rate of hole transport is DBTSI 3 > DBTSI 1 > DBTSI 2 > DBTSI 4. The DBTSI 3 has the highest hole transport rate and the lowest electron transport rate. Similar results were seen for the disubstituted cases as well.
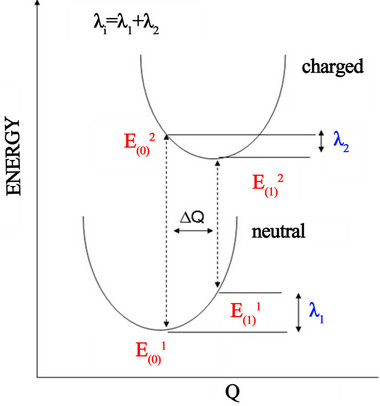
Figure 6. Schematic plot of reorganization energy.
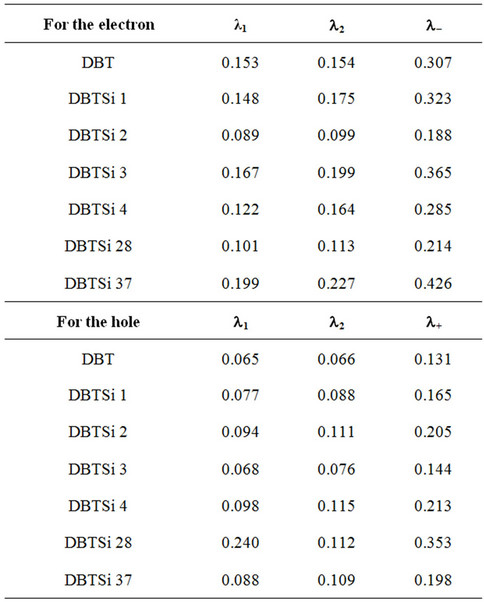
Table 6. The calculated reorganization energies.
3.5. Conclusion
Using theoretical methods we have described a set of molecules that are promising as electron transport materials for blue OLEDs. The ETms have sufficiently deep HOMO energies to block holes and high enough triplet energies to prevent exciton quenching. These materials have the chemical functionality to transport electrons and can be used as the electron transport/hole blocking layers in blue electro phosphorescent OLED devices.
4. Acknowledgements
This work was funded by the Solid Sate Lighting Program of the US Dept. of Energy, within the Building Technologies Program (BT), (Award Nos. M6743231 and M68004043) and managed by the National Energy Technology Laboratory (NETL). A portion of this research was performed using Environmental Molecular Sciences Laboratory (EMSL), which is a national scientific user facility sponsored by the Department of Energy’s Office of Biological and Environmental Research and is located at Pacific Northwest National Laboratory (PNNL). Computations were carried out using “NWChem, A Computational Chemistry Package for Parallel Computers, Version 5.1” (2007), developed at the High Performance Computational Chemistry Group, Pacific Northwest National Laboratory. Extensible Computational Chemistry Environment (ECCE), A Problem Solving Environment for Computational Chemistry, “Software Version 6.0” (2009), as developed and distributed by Pacific Northwest National Laboratory, and funded by the US Department of Energy, was used to obtain some of these results. Pacific Northwest National Laboratory is operated by Battelle Memorial Institute for the US Department of Energy (DOE) under Contract No. DEAC06-76RLO 1830.
REFERENCES
- C. W. Tang, “Organic Electroluminescent Cell,” US Patent No. 4356429, 1982.
- C. W. Tang and S. A. VanSlyke, “Organic Electroluminescent Diodes,” Applied Physics Letters, Vol. 51, No. 12, 1987, pp. 913-915. doi:10.1063/1.98799
- J. S. Swensen, E. Polikarpov, A. Von Ruden, L. Wang, L. S. Sapochak and A. B. Padmaperuma, “Improved Efficiency in Blue Phosphorescent Organic Light Emitting Devices Using Host Materials of Lower Triplet Energy than the Phosphorescent Blue Emitter,” Advanced Functional Materials, Vol. 21, No. 17, 2011, pp. 3250-3258. doi:10.1002/adfm.201100586
- S.-H. Eom, Y. Zheng, N. Chopra, J. Lee, F. So and J. Xue, “Low Voltage and Very High Efficiency Deep-Blue Phosphorescent Organic Light-Emitting Devices,” Applied Physics Letters, Vol. 93, No. 13, 2008, Article ID: 133309.
- E. Polikarpov, J. S. Swensen, N. Chopra, F. So and A. B. Padmaperuma, “An Ambipolar Phosphine Oxide-Based Host for High Power Efficiency Blue Phosphorescent OLEDs,” Applied Physics Letters, Vol. 94, No. 22, 2009, Article ID: 223304. doi:10.1063/1.3148642
- M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. J. van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. de Jong, “NWChem: A Comprehensive and Scalable Open-Source Solution for Large Scale Molecular Simulations,” Computer Physics Communications, Vol. 181, No. 9, 2010, pp. 1477-1489. doi:10.1016/j.cpc.2010.04.018
- G. Black, J. Chase, J. Chatterton, J. Daily, T. Elsethagen, D. Feller, D. Gracio, D. Jones, T. Keller, C. Lansing, S. Matsumoto, B. Palmer, M. Peterson, K. Schuchardt, E. Stephan, L. Sun, K. Swanson, H. Taylor, G. Thomas, E. Vorpagel, T. Windus and C. Winters, “ECCE, a Problem Solving Environment for Computational Chemistry, Software Version 6.3,” Pacific Northwest National Laboratory, Richland, Washington, 2011.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, “Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields,” Journal of Physical Chemistry, Vol. 98, No. 45, 1994, pp. 11623-11627. doi:10.1021/j100096a001
- “EMSL Basis Set Exchange,” 2012. https://bse.pnl.gov/bse/portal
- L. Cosimbescu, L. Wang, M. L. Helm, E. Polikarpov, J. S. Swensen and A. B. Padmaperuma, “Silane-Based Electron Transport Materials: Synthesis, Properties and Device Performance,” International Journal of Organic Chemistry, Vol. 2, No. 2, 2012, pp. 101-110. doi:10.4236/ijoc.2012.22016
- E. R. Davidson, “Comment on Dunning’s CorrelationConsistent Basis Sets,” Chemical Physics Letters, Vol. 260, 1996, pp. 514-518.
- L. Cosimbescu, A. B. Padmaperuma and D. J. Gaspar, “7,7,8,8-Tetracyanoquinodimethane Based Molecular Dopants for p-Type Doping of OLEDs: A Theoretical Investigation,” Journal of Physical Chemistry A, Vol. 115, No. 46, 2011, pp. 13498-13503.
- P. K. Koech, P. Evgueni, J. E. Rainbolt, L. Cosimbescu, J. S. Swensen, A. Von Ruden and A. Padmaperuma, “Synthesis and Application of Pyridine-Based Ambipolar Hosts: Control of Charge Balance in Organic Light Emitting Devices by Chemical Structure Modification,” Organic Letters, Vol. 12, No. 23, 2010, pp. 5534-5537.
- P. Evgueni, P. K. Koech, L. Wang, J. S. Swensen, L. Cosimbescu, J. E. Rainbolt, A. L. Von Ruden, D. J. Gaspar and A. B. Padmaperuma, “Controlling Charge Transport in Blue OLEDs by Chemical Functionalization of Host Materials,” Journal of Photonic Energy, Vol. 1, 2011, Article ID: 011007.
- C. Lelia, P. Evgueni, J. S. Swensen, J. T. Darsell and A. B. Padmaperuma, “Hole-Rich Host Materials for Blue Phosphorescent OLEDs,” Journal of the Society of Information Display’s, Vol. 19, No. 4, 2011, pp. 353-359. doi:10.1889/JSID19.4.353
- A. B. Padmaperuma, P. K. Koech, L. Cosimbescu, E. Polikarpov, J. S. Swensen, N. Chopra, F. So, L. S. Sapochak and D. J. Gaspar, “Tuning Charge Balance in PHOLEDs with Ambipolar Host Materials to Achieve High Efficiency,” Organic Light Emitting Materials and Devices XIII, Vol. 7415, 2009.
- P. K. Koech, L. S. Sapochak, J. E. Rainbolt, L. Cosimbescu, E. Polikarpov, J. S. Swensen, L. F. Wang, A. B. Padmaperuma and D. J. Gaspar, “Design of New Anchored p-Dopants for High Power Efficiency OLEDs,” Organic Light Emitting Materials and Devices XIII, Vol. 7415, 2009.
- L. S. Sapochak, A. B. Padmaperuma, X. Cai, J. L. Male and P. E. Burrows, “Inductive Effects of Diphenylphosphoryl Moieties on Carbazole Host Materials: Design Rules for Blue Electrophosphorescent Organic LightEmitting Devices,” Journal of Physical Chemistry C, Vol. 112, No. 21, 2008, pp. 7989. doi:10.1021/jp800079z
- T. Koopmans, “Über die Zuordnung von Wellenfunktionen und Eigenwerten zu den Einzelnen Elektronen Eines Atoms,” Physica, Vol. 1, No. 1-6, 1933, pp. 104- 113. doi:10.1016/S0031-8914(34)90011-2
- H. Geng, Y. Niu, Q. Peng, Z. Shuai, V. Coropceanu and J.-L. Brédas, “Theoretical Study of Substitution Effects on Molecular Reorganization Energy in Organic Semiconductors,” Journal of Chemical Physics, Vol. 135, No. 10, 2011, Article ID: 104703.
- P. J. Hay, “Theoretical Studies of the Ground and Excited Electronic States in Cyclometalated Phenylpyridine Ir(III) Complexes Using Density Functional Theory,” Journal of Physical Chemistry A, Vol. 106, No. 8, 2002, pp. 1634- 1641.
- A. Curioni, W. Andreoni, R. Treusch, F. J. Himpsel, E. Haskal, P. Seidler, C. Heske, S. Kakar, T. van Buuren and L. Terminello, “Atom-Resolved Electronic Spectra for Alq3 from Theory and Experiment,” Applied Physics Letters, Vol. 72, No. 13, 1998, p. 1575.
- S. Y. Hong, D. Y. Kim, C. Y. Kim and R. Hoffmann, “Origin of the Broken Conjugation Inm-Phenylene Linked Conjugated Polymers,” Macromolecules, Vol. 34, No. 18, 2001, pp. 6474-6481.
- D. Kim, S. Salman, V. Coropceanu, E. Salomon, A. B. Padmaperuma, L. S. Sapochak, A. Kahn and J.-L. Bredas, “Phosphine Oxide Derivatives as Hosts for Blue Phosphors: A Joint Theoretical and Experimental Study of Their Electronic Structure,” Chemistry of Materials, Vol. 22, No. 1, 2010, pp. 247-254. doi:10.1021/cm9029616
- R. A. Marcus, “Electron Transfer Reactions in Chemistry. Theory and Experiment,” Reviews of Modern Physics, Vol. 65, No. 3, 1993, pp. 599-610. doi:10.1103/RevModPhys.65.599
- M. Bixon and J. Jortner, “Electron Transfer: From Isolated Molecules to Bimolecules,” Advances in Chemical Physics, Vol. 106-107, Wiley, New York, 1999.
- E. Polikarpov and A. B. Padmaperuma, “Materials Design Concepts for Efficient Blue OLEDs: A Joint Theoretical and Experimental Study,” Material Matters, Vol. 7, 2012, pp. 2-6.

