Received 4 June 2016; accepted 25 July 2016; published 28 July 2016

ABSTRACT

This article provides an alternative approach to estimate the functional coefficient ARCH-M model given by Zhang, Wong and Li (2016) [1] . The new method has improvement in both computational and theoretical parts. It is found that the computation cost is saved and certain convergence rate for parameter estimation has been obtained.

Keywords:

Functional Coefficient, ARCH-M Model, Consistency, Risk Aversion

1. Introduction

ARCH-M model (Engle et al. [2] ) has been widely studied in last decades due to its various applications. Specially, ARCH-M model gives a way to study the relationship between return and the volatility in finance (for instances, see [3] [4] ). Let 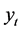denote the excess return of a market and 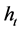denote the corresponding conditional vola- tility at time t. 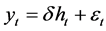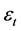A frequently applied conditional mean in ARCH-M models is with being an error term. The above equality gives a straightforward linear relationship between volatility and return: high volatility (risk) causes high return. The volatility coefficient can be addressed as relative risk aversion para- meter in Das and Sarkar [5] and price of volatility in Chou et al. [6] . Many empirical studies have been done based on the above conditional mean. However, some researchers found nonconstant and counter-cyclical [7] - [9] . To capture the variation of the volatility coefficient, Chou et al. [6] studied a time-varying parameter GARCH-M. In their GARCH-M model, the volatility coefficient was assumed to follow a random walk, namely 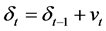with being an error term.

Based on Chou et al. [6] , it makes sense to study the ARCH-M model with a time-varying volatility coefficient. Motivated by the functional coefficient model, Zhang et al. [1] consider a class of functional coefficient (G) ARCH-M models. For simplicity, we focus on the functional coefficient ARCH-M model of the form

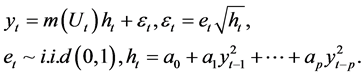(1)

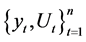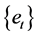Here are observable series and is independent of for.

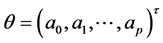is the unknown parameter vector and is an unknown smooth function. All throughout

this article, the superscript denotes the transpose of a vector or a matrix. In (1), the volatility coefficient is treated as some unknown smooth function. The conditional variance is assumed to be driven by a new-typed ARCH (p) process: the original is replaced by the observable. Similar to Chou et al. [6] , the modification for is helpful to estimate the model. In fact, such a setting for the conditional variance in (1) is not new, Ling [10] , Ling [11] , Zhang et al. [12] and Xiong et al. [13] have taken advantage of such specifications for the conditional variance. Considering in (1) as a measure of risk aversion as in Chou et al. [6] , the improvement of (1) lies in that it gives a way to understand how certain variable impacts the risk aversion.

For model (1), we need to estimate and based on the observable. In

Zhang et al. [1] , the estimation procedures is as follows.

Firstly, given, calculating based on the second equation of model (1);

Next, getting the estimator by functional coefficient regression technique based on the first equation of model (1), by treating as observable variable;

Thirdly, calculating residuals and acquiring by minimizing

with respect to, where is a known weight function.

It is shown in Zhang et al. [1] that the above estimation is consistent. However, there is no concrete conver- gence rate. Moreover, it can be seen that in the above estimation, depends on and hence depends on. However, there is no simple or explicite expression between them, which will make the calculation a bit time-consuming. In this article, a new simple estimator is given for model (1), which is shown to be consistent and convergence rate is also obtained.

The article is arranged as follows. In Section 2, we explain the idea about estimation approach. Section 3 lists the necessary assumptions to show the convergence results followed in Section 4. We conclude the paper in Section 5. Proofs of lemmas are put in the Appendix.

2. Estimation

For model (1), we need to estimate and based on the observable. Denote

to be the probability density function of. Let A be a compact subset of R with nonempty interior and satisfies. For each, based on (1) we have

(2)

where,. Given, define

(3)

Denote to be the true value for. Then, according to (2) and (3). Let and be corresponding local linear estimators for and respectively (Fan and Yao [14] ). Then we can define a estimator for as

(4)

For convenience of notation, we put

(5)

(6)

Further, define

(7)

(8)

(9)

where is a nonnegative weight function whose compact support is contained in A. Then, in terms of (3) and (9), estimators for and are given as

(10)

In the above estimation procedure, we follow the ideas from Christensen et al. [15] and Yang [16] . When, in (8) becomes the commonly used log-likelihood function in the literature. However the direct minimizer of with respect to is not practical because the quantity

in depends on the unknown function. Note that in (9) can be considered as an approximation to. Consequently, to obtain a feasible estimator for, we switch to minimize. For practical minimization in (10), one can refer the algorithm given by Christensen et al. [15] .

Remark 1. From (4), it can be seen that there is a simple specification between and. Such a simple explicite expression will greatly improve computational efficiency compared to the method in Zhang et al. [1] .

3. Assumptions

The following assumptions will be adopted to show some asymptotic results. Throughout this paper, we let denote certain positive constants, which may take different values at different places.

Assumption 1. The kernel function is a bounded density with a bounded support

Assumption 2. The process has a continuous pdf satisfying, where A is a compact subset of R with nonempty interior. Further, there are constants m and M such that

for.

Assumption 3. The considered parameter space is a bounded metric space. The process from (1) is strictly stationary and ergodic.

Assumption 4. holds uniformly for,

, where

Assumption 5. The function defined in (7) has an unique minimum point at.

Assumption 6. defined in (2) satisfy uniformly for

. The corresponding estimators suffice,

, where is the bandwidth such that and for some

and

Remark 2. Assumptions 1 - 3 are frequently adopted in the literature. Assumptions 4 - 5 have been analogously adopted by Yang [16] . In Assumption 6, the boundness is regular. When the bandwidth suffices the described conditions and the processes satisfies certain mixing conditions, the uniform convergence holds for local linear regression method (Fan and Yao [14] , Theorem 6.5).

4. Asymptotic Results

Theorem 1. Suppose that Assumptions 1 - 6 hold. Then for any

Theorem 1 shows our estimators are consistent. The following Theorem 2 further gives certain convergence rate.

Theorem 2. Suppose that Assumptions 1 - 6 hold. Then for any

In order to prove Theorem 1 and 2, we need the following lemmas whose proofs can be found in the Appendix.

Lemma 1. For and given in (3) and (4), suppose that Assumptions 1 - 6 hold. Then for

(11)

Lemma 2. For and given in (8) and (9), suppose Assumptions 1 - 6 hold. Then for

(12)

Proof of Theorem 1. From (7)-(8), it is not difficult to get

(13)

Here, for each takes value between and. Similar to (A.18), when, it can be shown

(14)

holds for certain finite M. Put

(15)

According to (A.18) and (A.19), (13)-(15), for certain M, it follows

(16)

Note is independent of and Then similar to (A.22), it can be shown that

, implying. Applying Lemma 1 and Theorem 1 in Andrews [17] to, then it follows that

(17)

(12) and (17) give

(18)

which implies the consistency of in (10) by Lemma 14.3 (page 258) and Theorem 2.12 (page 28) in Kosorok [18] . In addition,

where is between and.

Proof of Theorem 2. According to (10) and (12), it follows

(19)

where,

(20)

From Theorem 1 and Lemmas 1 - 2,

(21)

In the above second equality, the first is from the consistency of. Put

From (A.9),

(22)

By the martingale central limit theorem (see, for example, Theorem 35.12 in Billingsley [19] ), it is not difficulty to show

(23)

According to (19)-(23), it follows that

(24)

Moreover,

(25)

Conjecture. According to (19)-(25), if one can show, then we can state the following asymp- totic normality:

where

5. Conclusions

In this paper, a new approach is proposed to estimate the functional coefficient ARCH-M model. The proposed estimators are more efficient and, under regularity conditions, they are shown to be consistent. Certain convergence rate is also given.

Besides that the proof of conjecture in Section 4 needs further development, it is meaningful to further consider a GARCH type conditional variance in model (1). However, such an improvement is not trivial because the estimation method adopted in this paper can not be applied to the GARCH case. An alternative approach needs further development.

Acknowledgements

We thank the Editor and the referee for their comments. Research of X. Zhang and Q. Xiong is funded by National Natural Science Foundation of China (Grant No. 11401123, 11271095) and the Foundation for Fostering the Scientific and Technical Innovation of Guangzhou University. These supports are greatly appreciated.

Cite this paper

Xingfa Zhang,Qiang Xiong, (2016) An Alternative Estimation for Functional Coefficient ARCH-M Model. Theoretical Economics Letters,06,647-657. doi: 10.4236/tel.2016.64070

References

Appendix

Proof of Lemma 1

Proof. We only show the case of. Other situations can be proved by similar argument. Let

and. Then can be written as, can be

written as Noting, for, equals 1 when, and 0 for

other cases. Then it is easy to have

(A.1)

Hence,

(A.2)

According to Assumption.6, it is easy to obtain the following equalities:

(A.3)

Note that and implying

. Then Equation (11) follows from (A.2)-(A.3).

Proof of Lemma 2

Proof. We only consider the case of, other cases can be obtained with similar and easier arguments. From (5)-(6),

(A.4)

Further,

(A.5)

Let

(A.6)

Then,

(A.7)

We can further have

(A.8)

(A.9)

From (A.9), can be easily obtained by replacing with. Then

(A.10)

Here,

(A.11)

(A.12)

(A.13)

(A.14)

(A.15)

. (A.16)

Note because of Hence to show (12), it suffices to prove

To save space, we only give detailed proof of

It is easy to have

In terms of (A.4)-(A.5), can be written as

(A.17)

Without loss of generality, there exists a such that According to (5), Assumptions 2 and 5, when,

(A.18)

The last inequality comes from the fact is uniformly bounded for. Similarly, when we can show

(A.19)

From Lemma 1, it follows that

(A.20)

(A.17)-(A.20) gives

(A.21)

Note that is independent of and. Based on Assumption 3, we have

(A.22)

(A.20)-(A.22) implies.

Submit or recommend next manuscript to SCIRP and we will provide best service for you:

Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.

A wide selection of journals (inclusive of 9 subjects, more than 200 journals)

Providing 24-hour high-quality service

User-friendly online submission system

Fair and swift peer-review system

Efficient typesetting and proofreading procedure

Display of the result of downloads and visits, as well as the number of cited articles

Maximum dissemination of your research work

Submit your manuscript at: http://papersubmission.scirp.org/

NOTES

^*Corresponding author.