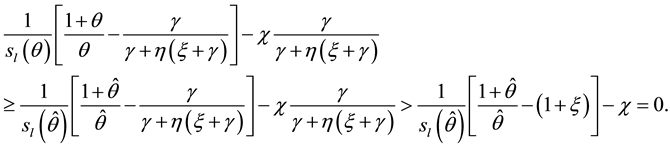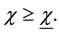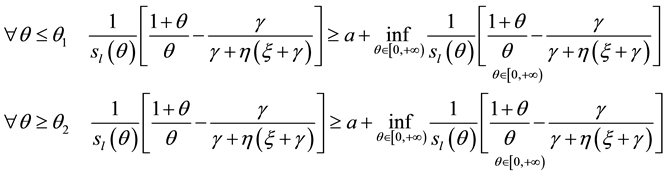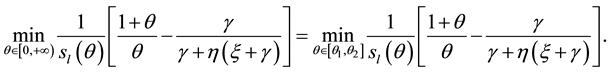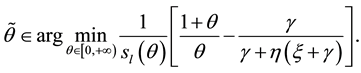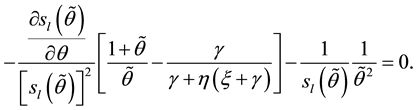Theoretical Economics Letters
Vol.05 No.06(2015), Article ID:61769,7 pages
10.4236/tel.2015.56082
Dynamic Inconsistency and the Seignorage Paradox
Fernando Perera-Tallo
Universidad de

Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 25 October 2015; accepted 5 December 2015; published 8 December 2015

ABSTRACT
Why do governments that pursue seignorage set growth rates of money that exceeds the one that maximizes it? This paper presents a Keynesian model with a government that pursues seignorage but dislikes inflation. Dynamic inconsistency problems prevent the implementation of the optimal growth rate of money and even the existence of stationary equilibrium. When stationary equilibrium exists, it is multiple and the growth rate of money is larger than the one that maximizes seignorage in some or even all equilibria.
Keywords:
Seignorage, Dynamic Inconsistency, Monetary Policy

1. Introduction
Seignorage is the real value of the revenues that the government receives from the emission of money. Seignorage may be seen as the revenues of the “inflation tax”. The reason is that the emission of money generates inflation, which implies that money holders suffer a lost for the reduction in the value of their money balances. These losses may be seen as a “tax” on money balances and seignorage is the revenues from this “inflation tax”. While an increment in the growth rate of money always increases inflation, it does not always increase seignorage, since there is a growth rate of money that maximizes seignorage. If the growth rate of money exceeds such level, seignorage goes down. That is, the tax revenue of the “inflation tax” goes down but the tax burden, the inflation rate, goes up. At first glance, it seems that no government has incentives to do such self-defeating policy. However, several historical episodes, in particular hyperinflations, suggest that governments with desperate need for seignorage have set growth rates of money that exceeds the one that maximizes it. This paper analyzes the decision by governments about seignorage and proposes an explanation for the paradox of governments that choose to exceed the growth rate of money that maximizes seignorage.
This paper presents a standard Keynesian model with a government that pursues seignorage but dislikes inflation. That is, the government’s objective function increases with seignorage but decreases with inflation. We distinguish between the long run, in which agents can perfectly foresee the inflation rate, and the short run, in which expectation about inflation may be wrong. A hump-shape relationship between seignorage and growth rate of money arises at the long run. The mechanism behind this result resembles to a Laffer curve. As we explain above, the inflation tax is a tax over money balances, where the tax rate is the growth rate of money, which in the long run is equal to the inflation rate, and the tax base is the real amount of money. When the growth rate of money goes up, the tax rate goes up, but the tax base, real money, goes down. This occurs since money holders perfectly foresee inflation at the long run and they reduce their demand for money. When the growth rate of money is low, seignorage rises with it up to the point in which riches its maximum level. After that, increasing the growth rate of money is counterproductive for raising further seignorage, since the effect of reducing the tax base, the real amount of money, overtakes the effect of rising the tax rate, the growth rate of money. In fact, since government does care not only about seignorage but also about inflation, the growth rate of money that maximizes the objective function of government at the long run, the optimal growth rate of money, is strictly below the growth rate that maximizes seignorage.
The behavior of seignorage at the short run is totally different. The key reason for this is linked to the definition of short run: the absence of perfect information and the possibility of wrong expectations. Since the model is Keynesian, an “unanticipated” increase of the growth rate of money expands income and reduces the nominal interest rate. Both of these factors will increase the demand for money and the real amount of it. Consequently, an increase on the growth rate of money will increase not only the “tax rate” of the “inflation tax”, the growth rate of money, but also the tax base, the real amount of money. Consequently, seignorage at the short run always increases with the growth rate of money. This implies a problem of dynamic inconsistency: if agents believe that the government is going to set the optimal growth rate of money, the government will have incentives to set a growth rate of money larger than the optimal one. This dynamic inconsistency problem implies that the growth rate of money and the inflation rate at the stationary equilibrium will be always larger than the optimal level.
Furthermore, dynamic inconsistency not only makes suboptimal the equilibrium; it may even prevent the existence of stationary equilibria. If government’s aversion for inflation is not large enough, it always will have incentives to set a growth rate of money that is above the expected inflation rate of agents in order to get more seignorage. This will prevent the existence of stationary equilibria. When government’s aversion for inflation is large enough, stationary equilibrium does exist but multiple stationary equilibria arise. Furthermore, the growth rate of money is not only larger than the optimal level but also larger than the growth rate that maximizes seignorage at the long run in at least one stationary equilibrium. In fact, if government’s aversion to inflation is not high enough, the growth rate of money is larger than the one that maximizes seignorage in all the stationary equilibrium. Thus, our paper provides an explanation for the paradox of governments that pursue seignorage but set growth rates of money that exceed the one that maximizes it.
Classical papers about dynamic inconsistency of monetary policy include [1] -[3] . These papers do not analyze seignorage, which is the focus of our paper.
This paper does not analyze hyperinflation. Nevertheless, the paper sheds light on the incentives that governments may have to set a growth rate of money above its natural upper bound: the growth rate of money that maximizes seignorage. Thus, the paper contributes to better understanding the incentives that government may have to set a “very high” growth rate of money which in turns may generate hyperinflation. In this sense, the paper contributes to the hyperinflation literature, which considers the seignorage as an exogenous variable and does not explain the incentives that the government may have to generate hyperinflation. See among others [4] - [6] and the revision of this literature by [7] and [8] and the papers quoted there.
2. The Model
2.1. Setup
The model is a standard Keynesian model with the following equations:
IS curve:
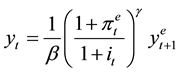 (1)
(1)
LM curve:
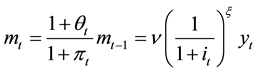 (2)
(2)
Supply curve:
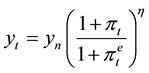 (3)
(3)
where y denotes real income, p denotes inflation rate, i denotes nominal interest rate, m real amount of money and
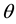 the growth rate of the nominal supply of money. b, g, x, n, h and
the growth rate of the nominal supply of money. b, g, x, n, h and
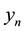 are parameters. The sub-index t denotes period, while the super-index “e” means expectative.
are parameters. The sub-index t denotes period, while the super-index “e” means expectative.
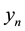 denotes the natural income, that is, the income at the equilibrium when the expectations of agents are correct. Note these equations are the ones of a New Keynesian model (see Chapter 6 of [9] ). The exception is the demand for money (right hand of Equation (2)). There are two reason for this modification: first tractability; second, the demand for money1 in the standard New Keynesian model tends to infinity when the nominal interest rate tend to zero. Thus, at the short-run the government would be able to get an “infinite” amount of resources from seignorage by setting a growth rate of money that make the nominal interest rate zero. Such feature makes this functional form not suitable for a paper that focuses on seignorage.
denotes the natural income, that is, the income at the equilibrium when the expectations of agents are correct. Note these equations are the ones of a New Keynesian model (see Chapter 6 of [9] ). The exception is the demand for money (right hand of Equation (2)). There are two reason for this modification: first tractability; second, the demand for money1 in the standard New Keynesian model tends to infinity when the nominal interest rate tend to zero. Thus, at the short-run the government would be able to get an “infinite” amount of resources from seignorage by setting a growth rate of money that make the nominal interest rate zero. Such feature makes this functional form not suitable for a paper that focuses on seignorage.
Solving the model, we get that:
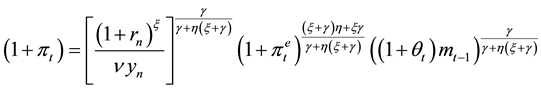 (4)
(4)
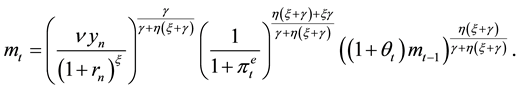 (5)
(5)
It is important to note that, at the short run, the real amount of money increases with the growth rate of money, due to the Keynesian features of the models. An expansionary monetary policy reduces the nominal interest rate and raises income. Both effects raise the demand and the real amount of money.
We define stationary equilibrium at the long run as an equilibrium in which the expectation of agents are correct, the money growth rate is constant and the real amount of money is constant. That is,
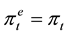 and
and
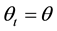 and
and . It follows from (4) and (5) that at the long run:
. It follows from (4) and (5) that at the long run:
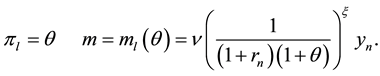 (6)
(6)
2.2. Seignorage
Seignorage is the real amount of resources that government obtains from emitting money. We assume that the fraction of money that is emitted by the government is constant and denoted by y (that is, the monetary multiplayer is 1/y). Thus, the seignorage, denoted by s, is as follows:
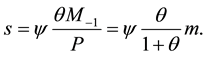 (7)
(7)
The amount of seignorage at the long run would be as follows (see 6 and 7):
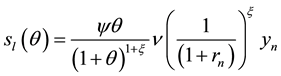
The relationship between the growth rate of money and the seignorage has hum shape:
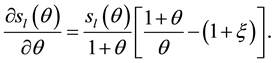
The seignorage at the long run reaches its maximum value when the growth rate of money is equal to
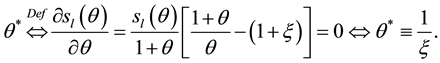
The maximum seignorage at the long run is denoted by
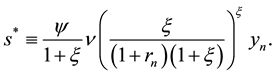
The growth rate of money always raises the “nominal seignorage” and the portion of real money that goes to seignorage, that is,
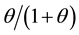
The seignorage at the short-run is as follows (see 5 and 7):
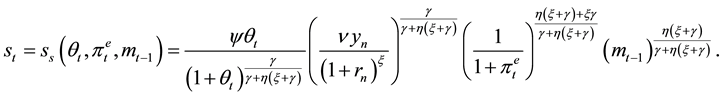
The seignorage at the short-run increases always with the growth rate of money:
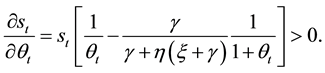
The Keynesian features of the model deliver the above result. An expensive monetary policy reduces at the short run the nominal interest rate and increases the income. Both effects raise the demand for money and, consequently, the real amount of money, which implies a higher seignorage. Note that if the supply of goods were perfectly inelastic,
3. Government
We will assume that the utility function of government is as follows:
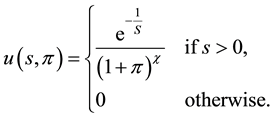
We define optimal growth rate of money2 as the growth rate of money that maximizes the government’s utility function at the stationary long run equilibrium:
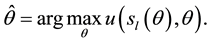
Proposition 1: There is a unique optimal growth rate of money. Such optimal growth rate is always in the interval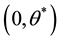
Proof:
The FOC of the problem (12) may be written as follows:
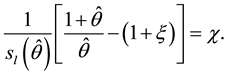
Then
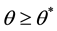
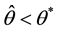
When
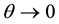
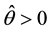
Since the above function is strictly decreasing in the interval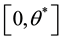
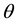
The maximization problem of government (at the short run) would be as follows:
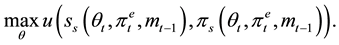
The FOC of the above problem when
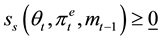
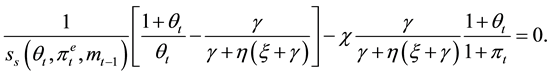
In a stationary equilibrium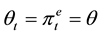
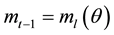
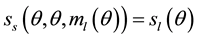
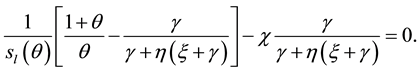
Proposition 1: In any stationary equilibrium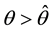
Proof:
Note that for any
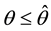
Thus, the growth rate of money and the inflation rate are always above the optimal level. The reason for that is dynamic inconsistency: if the agents believe that the growth rate of money is going to be the optimal one, the government has incentive to deviate and set a growth rate of money above the optimal level.
Proposition 2: There is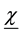
Proof:
Let’s define
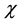
Note that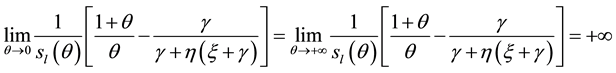
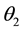
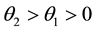
where
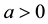
Since the above function is continuous in the interval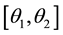
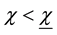
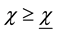
Thus, stationary equilibrium exists only if government aversion to inflation is high enough. Otherwise, the government will always have incentives to “cheat” agents and set a growth rate of money and an inflation rate that exceed the expected inflation of agents in order to get more seignorage. Thus, dynamic inconsistency may prevent the existence of a stationary equilibrium.
Proposition 3: If
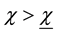
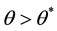
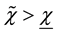

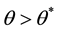
Proof:
Let’s define
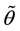
We have proven already that the above minimum exist (see previous proof). Furthermore
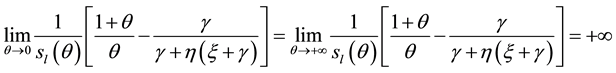
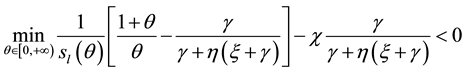
In order that the above equation holds
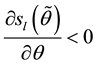
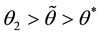
Finally, let’s define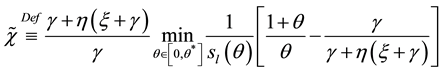
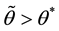
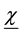
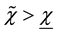
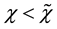
Thus, the growth rate of money is not only higher than the optimal level; it is also, at least in some equilibrium, higher than the growth rate of money that maximizes seignorage. When government aversion for inflation is not high enough, the growth rate of money is higher than the one that maximizes seignorage in all equilibria. Thus, dynamic inconsistency may explain the paradox of governments that pursue seignorage but set growth rates of money that exceeds the one that maximizes it.
4. Conclusions
Why do governments that pursue seignorage set growth rates of money that exceeds the one that maximizes it? In order to understand this paradoxical behavior, this paper has presented a Keynesian model in which government cares about seignorage and inflation. There is a hump-shape relationship between seignorage and the growth rate of money at the long run. The growth rate of money that maximizes the government objective function at the long run (called optimal growth rate of money) is always below the growth rate of money that maximizes seignorage. Nevertheless, due to the Keynesian properties of the model, the relationship between growth rate of money and seignorage at the short run is increasing. This implies a dynamic inconsistency problem: if agents believe that growth rate of money is going to be the optimal one, the government has incentives to “cheat” agents and set a growth rate of money higher than the optimal one. Thus, dynamic inconsistency implies a higher growth rate of money than the optimal one. Furthermore, dynamic inconsistency may even prevent the existence of stationary equilibrium. This happens when the government has incentives to “cheat” agents and set a growth rate of money and an inflation rate that exceeds the expected inflation. The long run behavior of the economy depends on the degree of aversion to inflation by government. When the aversion to inflation is low, stationary equilibrium does not exist. Otherwise, there are multiple equilibria. When the aversion to inflation is in a middle range, the growth rate of money is higher than the one that maximizes seignorage in every equilibrium. Finally, even when the aversion to inflation is high, the growth rate of money is larger than the one that maximizes seignorage at the long run in some equilibria. Thus, the paper explains the paradox of governments that pursue seignorage but set growth rates of money that exceed the one that maximize it.
This paper focuses on stationary equilibrium and calls for fully analyzing the dynamic of the model in future research.
Acknowledgements
The author acknowledges the financial support from the “Ministerio de Economía y Competitividad” (Project ECO2013-48884-C3-3-P).
Cite this paper
FernandoPerera-Tallo, (2015) Dynamic Inconsistency and the Seignorage Paradox. Theoretical Economics Letters,05,713-719. doi: 10.4236/tel.2015.56082
References
- 1. Barro, R.J. and Gordon, D.B. (1983) Rules, Discretion and Reputation in a Model of Monetary Policy. Journal of Monetary Economics, 12, 101-121. http://dx.doi.org/10.1016/0304-3932(83)90051-X
- 2. Calvo, G. (1978) On the Time Consistency of Optimal Policy in a Monetary Economy. Econometrica, 46, 1411-1428. http://dx.doi.org/10.2307/1913836
- 3. Kydland, F.E. and Prescott, E.C. (1977) Rules Rather than Discretion: The Inconsistency of Optimal Plans. Journal of Political Economy, 85, 473-492. http://dx.doi.org/10.1086/260580
- 4. Bruno, M. and Fischer, S. (1990) Seigniorage Operating Rules and the High Inflation Trap. The Quarterly Journal of Economics, 105, 353-374. http://dx.doi.org/10.2307/2937791
- 5. Cagan, P. (1956) The Monetary Dynamics of Hyperinflation. In: Friedman, M., Ed., Studies in the Quantity Theory of Money, The University of Chicago Press, Chicago, 25-117.
- 6. Evans, J.L. and Yarrow, G. (1981) Some Implications of Alternative Expectations Hypotheses in the Monetary Analysis of Hyperinflations. Oxford Economic Papers, 33, 61-80.
- 7. Sokic, A. (2011) The Monetary Analysis of Hyperinflation and the Appropriate Specification of the Demand for Money. German Economic Review, 13, 142-160. http://dx.doi.org/10.1111/j.1468-0475.2011.00543.x
- 8. Vazquez, J. (1998) How High Can Inflation Get during Hyperinflation? A Transaction Cost Demand for Money Approach. European Journal of Political Economy, 14, 433-451. http://dx.doi.org/10.1016/S0176-2680(98)00016-0
- 9. Romer, D. (2010) Advanced Macroeconomics. 4th Edition, McGraw-Hill.
- 10. Díaz, A. and Perera-Tallo, F. (2011) Credit and Inflation under Borrower’s lack of Commitment. Journal of Economic Theory, 146, 1888-1914. http://dx.doi.org/10.1016/j.jet.2011.03.015
NOTES
1The standard demand for money in a new Keynesian model is as follows:
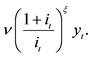
2This concept of optimality is completely different from the one used by the Friedman’s rule literature, in which the optimal inflation rate is usually negative. An exception is [10] .