Theoretical Economics Letters
Vol.05 No.03(2015), Article ID:56720,6 pages
10.4236/tel.2015.53044
Modeling the Relationship between Restaurant Tipping and Consumer Behavior
Tin-Chun Lin
School of Business and Economics, Indiana University-Northwest, Gary, IN, USA
Email: tinlin@iun.edu
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 April 2015; accepted 24 May 2015; published 27 May 2015
ABSTRACT
The theory of consumer choice was applied to model the relationship between restaurant tipping and consumer behavior. Using this model, we showed how consumer behavior responds to restaurant tipping and how tipping affects consumer-utility among different types of consumers and economic efficiency. The theoretical analysis reveals that tipping discourages customers’ demand for restaurant meals, which in turn creates bigger excess burden in the market.
Keywords:
Restaurant Tipping, Consumer Behavior, Excess Burden

1. Introduction
Restaurant tipping is a worldwide custom. The voluntary nature of tipping raises a number of questions, such as why do people tip, do patrons tip a fixed percentage of the bill size, are tips based on a conscientious appraisal of service, and do frequent customers tip more than infrequent customers for the same amount of service? Indeed, several studies reported in the psychology literature have significantly contributed to the answers to these questions (e.g., Freeman, Borden, and Latane, 1975 [1] ; Lynn and Latane, 1984 [2] ; Lynn, 1988 [3] ; Lynn and Grassman, 1990 [4] ; Bodvarsson and Gibson, 1994 [5] ; May, 1978 [6] ; Crusco and Wetzel, 1984 [7] ).
It should be noted that tipping may have originated in the taverns of 17th century in England, where drinkers would leave some money on the table to waiters “to insure promptitude” (T.I.P.). This custom had been brought to America since it had been colonized by English and began to make its way into taverns and dining halls. It now becomes a worldwide custom.
Although a number of previous studies have provided significant answers to the questions listed above, none have modeled the relationship between restaurant tipping and consumer behavior, i.e., whether or not restaurant tipping would discourage consumers’ demand for restaurant meals, and how tipping affects consumers’ utility and economic efficiencies. (Note: We exclude fast-food restaurants, such as Burger King. There are no servers’ services in fast-food restaurants, so tips are not necessary.) Therefore, in this paper, we applied the theory of consumer choice to develop a theoretical model that shows how consumer behavior responds to restaurant tipping, and how tipping affects consumer-utility among different types of consumers and economic efficiency.
2. The Model
In this section, the theory of consumer choice is used to create a model to link the relationship between restaurant tipping and consumer behavior. Consider that a representative customer always consumes two goods: restaurant meals and general necessities (such as food). Denote the quantities of these two goods consumed as X and Y, respectively. Assume that this representative customer is a rational economic individual who follows “the law of demand”, and both of these two goods (restaurant meals and general necessities are all normal goods. When the customer dines in a restaurant, he/she always demands extra services or efforts from servers, such as taking orders, bringing dishes, pouring water, and so on. The extra service is denoted as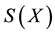 , which is a function of restaurant meals X. The more restaurant meals served, the greater the demand for extra services. Thus, the first derivative of extra service with respect to X is positive, i.e.,
, which is a function of restaurant meals X. The more restaurant meals served, the greater the demand for extra services. Thus, the first derivative of extra service with respect to X is positive, i.e.,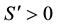 . But the second derivative of extra service with respect to X should be negative or equal to zero, i.e.,
. But the second derivative of extra service with respect to X should be negative or equal to zero, i.e., . This is because the additional demand for extra service is diminishing or constant. For convenience, assume that there is a linear relationship between the quantity of restaurant meals and extra services. Hence, the function of the extra services can be specified as follows:
. This is because the additional demand for extra service is diminishing or constant. For convenience, assume that there is a linear relationship between the quantity of restaurant meals and extra services. Hence, the function of the extra services can be specified as follows:
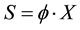 , (2.1)
, (2.1)
where  and f a parameter, an exogenous variable, such as the reputation and the location of the restaurant. If the restaurant were located in a metropolitan area and had a well-known reputation, f would be larger.
and f a parameter, an exogenous variable, such as the reputation and the location of the restaurant. If the restaurant were located in a metropolitan area and had a well-known reputation, f would be larger.
Assume that the customer’s utility function displays a simple form of Cobb-Douglas, such as
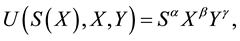 (2.2)
(2.2)
where 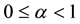 and
and . All a, b, and g are constant parameters, exogenous variables. It should be noted that a indicates the degree to which the customer desires extra service. If a is equal to zero, then the customer does not demand extra services, or the customer does not think that those services (such as taking orders, bringing dishes, and pouring water) are extra services. In addition, the larger the quantities of extra services, restaurant meals, and general necessities, the higher the customer’s utility; thus,
. All a, b, and g are constant parameters, exogenous variables. It should be noted that a indicates the degree to which the customer desires extra service. If a is equal to zero, then the customer does not demand extra services, or the customer does not think that those services (such as taking orders, bringing dishes, and pouring water) are extra services. In addition, the larger the quantities of extra services, restaurant meals, and general necessities, the higher the customer’s utility; thus,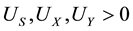 . Also, according to the law of diminishing marginal utility,
. Also, according to the law of diminishing marginal utility,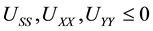 . We substitute Equation (2.1) into Equation (2.2), so the consumer’s utility can be rewritten as follows:
. We substitute Equation (2.1) into Equation (2.2), so the consumer’s utility can be rewritten as follows:
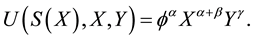 (2.3)
(2.3)
Suppose that the consumer allocates his/her income, I, between X and Y. The prices of X and Y are 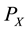 and
and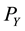 , respectively. Assume that a sales tax rate, t, is levied on X, but not on Y, since we assume that the state government does not levy a tax on general necessities, Y. After consuming a restaurant meal, X, suppose that the consumer always leaves t percentage of the total bill size as a tip on the table for servers. Therefore, the consumer’s budget constraint can be defined as follows:
, respectively. Assume that a sales tax rate, t, is levied on X, but not on Y, since we assume that the state government does not levy a tax on general necessities, Y. After consuming a restaurant meal, X, suppose that the consumer always leaves t percentage of the total bill size as a tip on the table for servers. Therefore, the consumer’s budget constraint can be defined as follows:
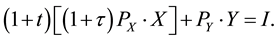 (2.4)
(2.4)
Choosing two goods, X and Y, can solve the consumer’s optimization problem, which maximizes Equation (2.3) and subjects the result to Equation (2.4). Thus, the Lagrangian expression is set up as follows:
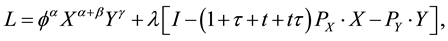 (2.5)
(2.5)
wherel stands for the Lagrangian multiplier or a shadow price. Meanwhile, Equation (2.5) yields the following first-order conditions for the constrained maximum:
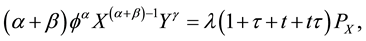 (2.6)
(2.6)

The first-order conditions are solved to yield the demand functions of X and Y, which are expressed as follows:

and

As Equations (2.8) and (2.9) show, given all parameters, the demand for restaurant meals, X, depends on the price of meals

Proposition 1.
If consumers are reluctant to tip although they tip all the time, and they do not think that taking orders, bringing dishes, and pouring water are extra services, then these consumers would be more likely to demand less for restaurant meals, X, and demand more for general necessities, Y.
Proof.
As defined earlier, a indicates the degree to which the customer desires extra service. If the customer does not think that taking orders, bringing dishes, and pouring water are extra services and is unwilling to tip for them, then the value of a would be very small or equal to zero. Set a = 0 and substitute it into Equations (2.8) and (2.9). The
new demand function of meals, 

new demand function of necessities, 

consumer would demand less for restaurant meals and more for general necessities. Q.E.D.
Proposition 2.
If no tips were necessary or there were not a worldwide custom for tipping, restaurant owners/managers would be more likely to raise the meal price at a 
Proof.
In the event of a no-tips requirement, we set t = 0. However, no tips would affect the supply of servers and cause restaurant owners/managers to have to pay higher wages to servers, which in turn would raise the prices of restaurant meals. Restaurant owners/managers may raise the meal price at a rate 



tion of meals, 

Since the demand function of necessities, as Equation (2.9) shows, is not associated with tips, there will not be a change in the demand for general necessities (Y). Q.E.D.
Proposition 3.
There are four types of consumers in a restaurant. Type 1 consumers do not desire any extra services and do not think that taking orders, bringing dishes, and pouring water are extra services so that they do not tip for them. Type 2 consumers may tip because they are guided by certain social norms and expectations. They would feel guilty if they did not tip, or they may want to obtain satisfaction from making a good impression on the server or on their fellow diners. Type 3 consumers also tip because they desire extra services from servers. They may not care or feel okay if they tip. Type 4 consumers desire services from servers, but they think that taking orders, bringing dishes, and pouring water are part of servers’ job and the price of the meal has already covered those services, so they don’t tip for them. Theoretically, type 4 consumers’ utility is the highest among the four types of consumers, type 1 consumers’ is the second, and type 2 consumers’ is the third highest. However, type 3 consumers’ utility may be the lowest.
Proof.
For type 1 consumers, we set both a and t to zero, and substitute Equations (2.8) and (2.9) into Equation (2.3); the utility of type 1 consumers can be obtained as follows:
Similarly, for type 2 consumers, we set a = 0 and t > 0; so the utility of type 2 consumers is:
For type 3 consumers, we set both a and t positive; thus, the utility of type 3 consumers can be generated as follows:
Finally, for type 4 consumers, we set a > 0 and t = 0; hence, the utility of type 4 consumers can be yielded as:
Comparing




3. Comparative Static Analysis and the Tip Elasticity of Demand
In addition to the first order condition shown in the last section, we further take a look at the second order conditions in this section, given constant parameters (a, b, g). Substitute Equation (2.6) into Equation (2.7) and obtain the following condition:

Further, we differentiate Equations (3.1) and (2.4) to get:

where


Let D be the determinant of the pre-multiplied matrix of vector










Intuitively, as Equations (3.3) and (3.4) show, budget improvement increases demands for both meals and necessities. As Equations (3.5) and (3.6) show, a rise in the price of meals would discourage consumers’ demand for meals, but does not provide consistent information about the other good-necessities. Similarly, as Equations (3.7) and (3.8) show, an increase in the price of necessities leads to fewer demands for them and uncertainty about the other good-meals. In addition, as Equations (3.9) and (3.10) show, a higher sales tax rate levied on meals reduces the demand incentives on the good, but the effect is uncertain on the other good. Finally, as Equations (3.11) and (3.12) show, if the tipping rate increases for restaurant meals, customers would be more likely to demand less for meals, but the effect is uncertain on necessities.
Based upon the comparative static analysis, a higher tipping rate would likely discourage a consumer’s demand for restaurant meals. In order to know the effect of an increase in the tipping rate on demand for meals, it is necessary to discuss the tip elasticity of demand.
According to the demand function of meals, as shown in Equation (2.8), the absolute value of the tip elasticity of demand, 

As Equation (3.13) shows, the absolute value of the tip elasticity of demand is less than 1, which means that it is inelastic. For example, if the current tipping rate is 15% of total bill size, then
4. Excess Burden
To understand if restaurant tipping would lead to greater excess burden (i.e., deadweight loss) in the market, in this section, we design a simple model of demand-supply in the market of restaurant meals, and ascertain the size of the excess burden of taxes and tips. Suppose that the demand function of restaurant meals is: 


Proposition 4.
Without tax and tip, at equilibrium, the market price is

Figure 1).
Proof.
At equilibrium:


Proposition 5.
With tax but without tip, the market equilibrium price is



Proof.
With tax but without tip, the demand function of X becomes:
At equilibrium:






larger than
Proposition 6.
With taxes and tips, the market equilibrium price becomes



Figure 1).
Figure 1. The market for restaurant meals (X).
Proof.
With both tax and tip, the demand function of X becomes:
At equilibrium:
Thus, we can solve for 

However, consumers have to tip and pay the tax, so consumers pay:





Proposition 7.
If a sales tax is levied on customers, excess burden is created, and the size of the excess burden is



lead to greater excess burden in the market(see Figure 1).
Proof.
From Figure 1,



bigger than
5. Conclusion
In summary, the main contribution and innovation of this paper are that we developed a theoretical model to link the relationship between restaurant tipping and consumer behavior. Using this model, we showed how consumer behavior responds to restaurant tipping and how tipping affects consumer-utility among different types of consumers and economic efficiency. The theoretical analysis shows that restaurant tipping does discourage demand for restaurant meals, which in turn creates bigger excess burden in the market.
References
- Freeman, S., Borden, M.R. and Latane, B. (1975) Diffusion of Responsibility and Restaurant Tipping: Cheaper by the Bunch. Personality and Social Psychology Bulletin, 1, 594-597. http://dx.doi.org/10.1177/014616727500100407
- Lynn, M. and Latane, B. (1984) The Psychology of Restaurant Tipping. Journal of Applied Social Psychology, 14, 551-563. http://dx.doi.org/10.1111/j.1559-1816.1984.tb02259.x
- Lynn, M. (1988) The Effects of Alcohol Consumption on Restaurant Tipping. Personality and Social Psychology Bulletin, 14, 87-91. http://dx.doi.org/10.1177/0146167288141009
- Lynn, M. and Grassman, A. (1990) Restaurant Tipping: An Examination of Three Rational Explanations. Journal of Economic Psychology, 11, 169-181. http://dx.doi.org/10.1016/0167-4870(90)90002-Q
- Bodvarsson, O.B. and Gibbson, W.A. (1994) Gratuities and Customer Appraisal of Service: Evidence from Minnesota Restaurants. The Journal of Socio-Economics, 23, 287-302.
- May, J.M. (1978) Tip or Treat: A Study of Factors Affecting Tipping Behavior. Unpublished M.A. Thesis, Loyola University of Chicago, Chicago.
- Crusco, A.H. and Wetzel, C.G. (1984) The Midas Touch: The Effects of Interpersonal Touch on Restaurant Tipping. Personality and Social Psychology Bulletin, 10, 512-517. http://dx.doi.org/10.1177/0146167284104003










