Theoretical Economics Letters
Vol.05 No.01(2015), Article ID:53594,4 pages
10.4236/tel.2015.51004
A Note on the Investment-Enhancing Effect of a Depreciated Real Exchange Rate
Pham Van Dai
Finders Business School, Flinders University, Adelaide, Australia
Email: Pham0109@flinders.edu.au
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 January 2015; accepted 20 January 2015; published 28 January 2015
ABSTRACT
This paper presents a mechanism through which a depreciated real exchange rate can lead to a higher investment rate. In an intertemporal framework, it shows that a depreciated real exchange rate can make the tradable sector more profitable and thus a greater requirement for capital. Moreover, the investment-enhancing effect of a depreciated real exchange rate decreases in magnitude when there is higher adjustment cost of investment.
Keywords:
Real Exchange Rate, Depreciation, Capital Accumulation, Adjustment Cost of Investment

1. Introduction
Despite an emerging literature on the role of the real exchange rate (RER) in the development process [1] - [4] , the theoretical understanding is still limited about the mechanism through which the growth enhancing effect of a depreciated real exchange rate is generated. Attention is focused mainly on the productivity channel [4] [5] and the capital accumulation channel [6] - [9] .
The forefront literature on the investment-enhancing effect of a depreciated RER is carried out in the context of Keynesian economics and the balance of payments constrained model [6] [8] . Gala (2008) focused merely on shortrun effects and showed the mechanism that a depreciated RER caused lower workers’ real wages and a higher firms’ margin, thereby stimulating investment. In a more comprehensive study, Porcile and Lima (2010) analyzed the channel referring to longer-term effects. They assumed excess demand for imported capital in developing countries that could not be matched because of balance of payments constraints. Therefore, a depreciated RER could promote exports , thus increasing foreign currency supply for imports in capital goods.
Rather than focusing on the shortrun effects of a depreciated RER, this paper examines the longrun relationship between a real depreciation and capital accumulation in a context of explicit, intertemporal utility maximization. In the model, the RER was defined internally as the relative price of tradable and non-tradable in the economy. To capture the stylized fact that tradable sectors are more capital-intensive in developing countries, an assumption has been made that capital is only used in the tradable sector of the theoretical economy.
2. The Model
2.1. The Production Function
Consider a small and open economy consisting of tradable and nontradable sectors. The tradable are produced by using capital and labor while the nontradable are produced by labor only. The tradable sector production function is assumed to be concave while there is a constant returning to scale production function in the nontradable sector. The economy is small enough that its production does not affect the international price of tradable.
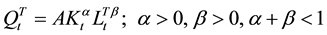 (1)
(1)
 (2)
(2)
where  and
and  denote the output of tradable and nontradable sectors.
denote the output of tradable and nontradable sectors. 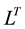 and
and 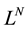 denote the number of labors in the tradable and nontradable sectors. As perfect labor mobility is assumed, labor unit cost is equal between tradable and nontradable sectors:
denote the number of labors in the tradable and nontradable sectors. As perfect labor mobility is assumed, labor unit cost is equal between tradable and nontradable sectors:
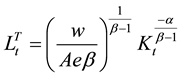 (3a)
(3a)
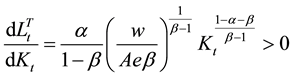 (3b)
(3b)
where is the real exchange rate defined as the relative price of tradable and nontradable. An increase in the value of e corresponds to a depreciation in the real exchange rate.
It is assumed that capital goods are not domestically produced and a representative firm in the tradable sector, with perfect foresight, maximizes its intertemporal profit after paying for imported capital goods and labor cost. Following the neoclassical theory of investment, the adjustment cost of investment is considered, and a strictly convex quadratic function of investment cost,  , is specified
, is specified
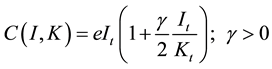 (4)
(4)
The representative firm’s optimization problem is to find the path of investment  to maximize its total discounted profit over an infinite horizon:
to maximize its total discounted profit over an infinite horizon:
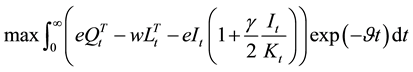 (5)
(5)
Subject to the law of motion of capital accumulation:
 (6)
(6)
where 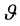 is the discount factor and
is the discount factor and 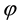 is the depreciation rate of capital goods. A dot over a variable signifies a time derivative. To simplify the exposition, the subscript
is the depreciation rate of capital goods. A dot over a variable signifies a time derivative. To simplify the exposition, the subscript 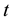 is dropped for the remainder of this paper.
is dropped for the remainder of this paper.
The current-value Hamiltonian is formed as below:

where 
Then the necessary conditions for the optimization:


Substitute (6) into (8):

Substitute (1), (3), and (8) into (9):

where

A solution to the maximization problem is a path satisfying conditions (10) and (11), and converging to the steady state.
2.2. Steady State
The steady state value of the costate variable 

Then substitute (13) into (11) and derive the steady state value of capital

Notably, a depreciation in the real exchange rate leads to higher steady state value of capital.

This result seems to be arguably counterintuitive given that capital goods are imported and real depreciation makes imports more expensive. The mechanism behind this result is that real depreciation reduces the real wage and hence makes the tradable sector more profitable. Since the tradable sector is more capital-intensive, there is a greater requirement for capital in the economy.
2.3. Linearized Dynamics
Consider the linearized dynamics of the system (10) and (11) at the steady state.

where




Because the determinant of the Jacobian matrix is negative, the roots are real and have opposite signs. The steady state is, therefore, a saddle point. Let 


Equation (19) implies that the rate of capital accumulation depends on the convergence speed, τ, and the distance to the steady state. Now consider a one-time, permanent, unanticipated depreciation in the real exchange rate and its effect on the growth rate of capital. Equation (15) shows that a depreciation shifts the steady state of capital to a higher level. Therefore, it lengthens the distance between an initial capital stock level and the steady state, and leads to a higher rate of capital accumulation.

It can be shown that the investment promotion effect of a depreciation in the real exchange rate decreases when the adjustment cost of investment increases.

Since


3. Conclusion
As noted by Montiel and Servén (2008), the literature so far mostly has focused on the empirical side of the relationship between a depreciated real exchange rate and economic growth, and the theoretical research addressing this issue is at a beginning state. This paper complements the existing literature by examining the effect a one-time, permanent and unanticipated depreciation in the real exchange rate on capital accumulation in an intertemporal model. We show that such a depreciation leads to a higher rate of capital accumulation, and that the magnitude of its effect depends negatively on the adjustment cost of investment.
References
- Bereau, S., Villavicencio, A.L. and Mignon, V. (2012) Currency Misalignments and Growth: A New Look Using Nonlinear Panel Data Methods. Applied Economics, 44, 3503-3511. http://dx.doi.org/10.1080/00036846.2011.577022
- Hausmann, R., Pritchett, L. and Rodrik, D. (2005) Growth Accelerations. Journal of Economic Growth, 10, 303-329. http://dx.doi.org/10.1007/s10887-005-4712-0
- Prasad, E.S., Rajan, R.G. and Subramanian, A. (2007) Foreign Capital and Economic Growth. Brookings Papers on Economic Activity, Vol. 1, 153-230. http://dx.doi.org/10.1353/eca.2007.0016
- Rodrik, D. (2008) The Real Exchange Rate and Economic Growth. Brookings Papers on Economic Activity, Vol. 2, 365-412. http://dx.doi.org/10.1353/eca.0.0020
- Eichengreen, B. (2007) The Real Exchange Rate and Economic Growth. Social and Economic Studies, 7-20.
- Gala, P. (2008) Real Exchange Rate Levels and Economic Development: Theoretical Analysis and Econometric Evidence.
- Montiel, P. and Servén, L. (2008) Real Exchange Rates, Saving and Growth: Is There a Link? World Bank Policy Research Working Paper Series, 4636.
- Porcile, G. and Lima, G.T. (2010) Real Exchange Rate and Elasticity of Labour Supply in a Balance-of-Payments- Constrained Macrodynamics. Cambridge Journal of Economics, 34, 1019-1039
- Razmi, A., Rapetti, M. and Skott, P. (2012) The Real Exchange Rate and Economic Development. Structural Change and Economic Dynamics, 23, 151-169. http://dx.doi.org/10.1016/j.strueco.2012.01.002


