Theoretical Economics Letters
Vol.4 No.5(2014), Article
ID:46610,9
pages
DOI:10.4236/tel.2014.45045
Valuation of Certificates on a Straddle with Forward Start—Theory and Evidence
Rodrigo Hernández1, Yinying Shao2
1Accounting, Finance and Business Law Department, Radford University, Radford, USA
2Finance Department, Towson University, Towson, USA
Email: rjhernand@radford.edu, yshao@towson.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 February 2014; revised 13 March 2014; accepted 30 March 2014
Abstract
This paper introduces a new financial product named Certificates on a Straddle with Forward Start and provides detailed descriptions of the product specifications. It shows that the payoff of a Certificate on a Straddle with Forward Start can be duplicated by the combination of long positions in call and put options on the underlying asset. A pricing formula is developed to price the certificates. A certificate issued by Credit Suisse is presented as an example to examine how well the model fits empirical data. The results show that issuing Certificates on a Straddle with Forward Start is a profitable business and the results are in line with previous studies pricing other structured products.
Keywords
Straddle, Forward Start Options, Option Pricing, Structured Products, Financial Innovation

1. Introduction
Over the last two decades, we have witnessed an explosive growth in volume, variety and complexity of modern structured financial products—i.e. newly created securities through the combination of fixed income securities, equities, and derivative securities [1] -[3] . The popularity of these products is mainly due to the relative high coupon rate paid by some of these products (e.g. Reverse Convertible Bonds) or the highly levered payoffs (e.g. Bonus Certificates, Outperformance Certificates, etc.) when the market interest rates are at all-time lows. For example, US dollar-denominated structured products became very popular in the era when the US Federal Reserve Bank consecutively lowered the federal fund rates 13 times from 6% on January 3, 2001 to 1% in June 2003—the lowest level in the previous six decades. Recently, we have experienced another run of decreasing federal fund rates. The Federal Reserve Bank lowered the federal fund rates 10 times from 5.25% on June 29, 2006 to between 0% and 0.25% in December 17, 2008—the all-time low. The appetite for higher returns would make structured products a natural choice.
However, investors are often required to take a high degree of risks that not always understand or are capable of assuming [4] -[10] . The potential loss of an investment in some types structured products could hypothetically result in a total loss of the invested capital. So, the current market conditions given (i.e. low interest rates and appetite for higher returns) combined with the complexity of these newly created financial instruments make the study of these securities more relevant than ever.
The purpose of the paper is to provide an in-depth economic analysis for the Certificates on a Straddle with Forward Start1 (to be referred to as CSFS henceforth) to explore how the principles of financial engineering are applied to the creation of such newly structured products. A pricing model for the certificates is developed by using option pricing formulas. In addition, an example of a CSFS issued on March 18, 2005 by Credit Suisse (to be referred to as CS henceforth), a well-recognized large bank in Europe, is presented. In this example, the certificate is priced by calculating the cost of a portfolio with a payoff similar to the payoff of the certificate.
The rest of the paper is organized as follows: the design of the certificates is introduced in Section 2; the pricing model is developed in Section 3; in Section 4, an example of CSFS is presented and the profit for issuing the certificate is calculated using the model developed in Section 3; Section 5 presents the conclusions.
2. Design of Certificates on a Straddle with Forward Start
The rate of return of a CSFS is contingent upon the price performance of its underlying asset over the last three months of its term to maturity. The beginning date of the term to maturity is known as the initial fixing date. The beginning date for calculating the gain (or loss) of the underlying asset is known as the strike setting date and the ending date of the term to maturity is known as the final fixing date. The certificate enables the investor to participate in the potential increase in the volatility of the underlying asset between the initial fixing date and the strike setting date. After the strike level is fixed, the certificate consists of a regular Straddle on the underlying asset. The strike level is set equal to a positive constant, α, times the price of the underlying asset on the strike setting date, and the final index level price equal to the underlying asset on the final fixing date.
If It is the underlying asset price on the strike setting date, (αIt) the strike level, and IT the final index level, then for an initial investment in one certificate, the total value that an investor will receive on the redemption date (known as the redemption price), VT, is equal to:
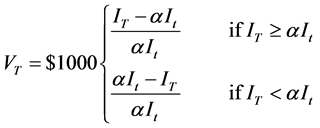 (1)
(1)
Alternatively, the relationship between the terminal value of a certificate and the terminal value of the underlying asset based on the change in the underlying asset price (without taking into account dividends) can be represented in Figure 1.
3. The Pricing of Certificates on a Straddle with Forward Start
The terminal value from Equation (1), VT, for an initial investment in one CSFS on strike setting date t, at-themoney (i.e. α = 1), and with term to maturity T, can be expressed mathematically as:
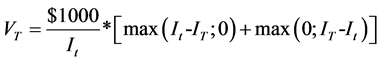 (2)
(2)
The max [IT-It; 0] in Equation (2) is the payoff for a long position in forward start European call options with exercise price It. The max [It-IT; 0] in Equation (2) is the payoff for a long position in forward start European put options with exercise price It. The $1000/It in Equation (2) is the number of put and call contracts needed per $1000 notional value of the certificate. The exact value of the number of contracts cannot be determined in advanced in year 0 since It is the price of the underlying asset on the strike setting date (i.e. year t). The best esti-
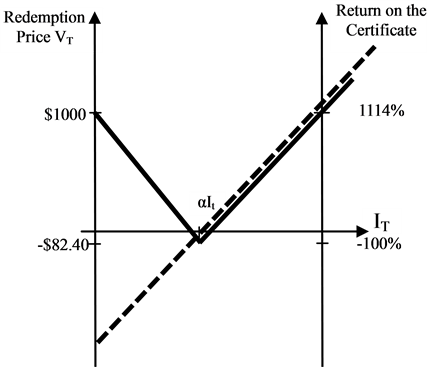
Figure 1. The terminal value and percentage return of an investment in one CSFS as a function of underlying asset price IT, with strike level equal to αIt, issue price equal to $82.40, and notional amount equal to $1000. The solid line represents the terminal value of the certificate on the final fixing date T, as a function of the terminal value of the underlying. The dashed line represents the terminal value of the underlying asset.
mation of the underlying asset’s price in year t using risk-neutral valuation would be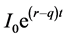 , the expected price in year t based on futures’ carry cost, where r is the risk-free rate of interest and q is the dividend yield rate of the underlying asset.
, the expected price in year t based on futures’ carry cost, where r is the risk-free rate of interest and q is the dividend yield rate of the underlying asset.
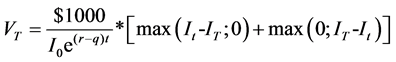 (3)
(3)
The payoff of one CSFS is exactly the same as the payoff for holding the following two positions:
1) A long position in forward start European call options on the underlying asset. The number of calls is , the exercise price of the option is It, and the term to expiration is T (which is the term to maturity of the certificate).
, the exercise price of the option is It, and the term to expiration is T (which is the term to maturity of the certificate).
2) A long position in forward start European put options on the underlying asset. The number of puts is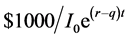 , the exercise price of the option is It, and the term to expiration is T (which is the term to maturity of the certificate).
, the exercise price of the option is It, and the term to expiration is T (which is the term to maturity of the certificate).
Since the payoff of a CSFS is the same as the combined payoffs of the above two positions, the fair value of the certificate can be calculated based on the value of the two positions. Any selling price of the certificate above the value of the above two positions is the gain to the certificate issuer. The value of Position 1 is the value of , shares of forward start European call options with time to maturity T, starting at-themoney at time t in the future, the strike is set equal to the underlying asset price at time t, and with each option having the value cfs [11] :
, shares of forward start European call options with time to maturity T, starting at-themoney at time t in the future, the strike is set equal to the underlying asset price at time t, and with each option having the value cfs [11] :
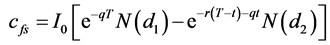 (4)
(4)
where
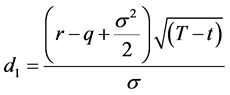 (5)
(5)
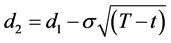 (6)
(6)
where σ is the standard deviation of the underlying asset returns.
Equation (4) can be simplified to [12] :
 (7)
(7)
where c is the value at time zero of an at-the-money call option that lasts for (T − t).2
The value of Position 2 is the value of  shares of forward start European put options with time to maturity T, starting at-the-money at time t in the future, the strike is set equal to the underlying asset price at time t, and with each option having the value pfs [11] :
shares of forward start European put options with time to maturity T, starting at-the-money at time t in the future, the strike is set equal to the underlying asset price at time t, and with each option having the value pfs [11] :
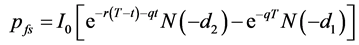 (8)
(8)
with d1 as in Equation (5) and d2 as in Equation (6). Equation (8) can be simplified to [12] :
 (9)
(9)
where p is the value at time zero of an at-the-money put option that lasts for (T − t).3 Therefore, the total cost, TC, for each certificate is
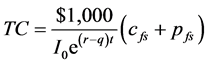
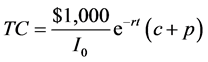 (10)
(10)
If B0 is the issue price of the certificate, any selling price above the fair value is the gain to the certificate issuer. And the profit function (Π) for the issuer is
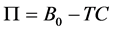 (11)
(11)
It is worth noting that, 1) when the exercise price of the option components is the same as the initial underlying asset price (I0), I0 vanishes from Equation (11). The fact that the profit function for issuing CSFS is independent of the initial price I0is a very important feature in the design of a CSFS because once a CSFS is designed, it can be issued any time before the strike setting date regardless the price of the underlying stock since the issuer’s profit will not be affected by this price; 2) all the “Greeks” of the certificates are similar to those of a long Straddle—the “Greeks” are quantities representing the certificates’ price sensitivities to a change in one input of the pricing formula at the time.
4. Empirical Test
In this section, a CSFS, denominated in US dollars, issued by Credit Suisse on March 18, 2005 using the Nasdaq-100 Index as the underlying asset is empirically examined. The major characteristics of the certificate are listed in Appendix 1 of the paper.
Based on the information in Appendix 1, the certificate was issued on March 18, 2005 with notional amount equal to $1000 and sold at $82.40. The strike setting date (i.e. the date on which the closing price of the underlying asset will be used as the initial index level) was set on December 16, 2005, approximately three months before the maturity date (or final fixing date). The final fixing date (i.e. the date on which the closing price of the underlying asset will be used as the final index level) was set on March 17, 2006, approximately one year later than the issue date (or initial fixing date). In order to calculate the issuer’s profit, the following data is needed for the certificate: 1) the price of the underlying asset, I0, 2) the cash dividends to be paid by the underlying assets and the ex-dividend dates so the dividend yield, q, can be calculated, 3) the risk-free rate of interest, r, and 4) the volatility of the underlying asset, σ. Equations (4), (7), and (8) are based on continuous dividend yield. Since dividends for the Nasdaq-100 Index are discrete, we calculate the equivalent continuous dividend yield. See Appendix 3 for the details of how equivalent continuous dividend yield rate is calculated from discrete dividends.
The prices and dividends of the underlying asset are obtained from Bloomberg; the risk-free rate of interest is the yield of government bonds (alternatively, swap rates) of which the term to maturity match those of the certificate. If a government bond that matches the term of maturity for a particular certificate cannot be found, the linear interpolation of the yields from two government bonds that have the closest maturity dates surrounding that of the certificate are used. The volatility (σ) of the underlying asset is the historical volatility calculated from the underlying securities prices in the previous 260 days is used. The one-year rate of interest, r, on March 18, 2005, the initial fixing date of the certificate, based on the US Dollar swap rates is 3.684%. The dividend yield, q, of the Nasdaq-100 Index is 0.43%. The Nasdaq-100 Index value on the initial fixing date of the certificate, I0, is 1484.40. The implied volatility of the Nasdaq-100 Index based on the stock options is 16.27% on the issue date. The cost of carry forward is 1532.52. Therefore, the total cost of issuing one CSFS, TC, based on Equation (10) is

 (12)
(12)
The profit for issuing each the certificate, π, is
 (13)
(13)
So the profit for issuing each CSFS is approximately $19.02. There are several ways to examine the reasonableness of the profit (or the quality of the model). One way to test the quality of the model is to examine the profit on the certificate. Since the cost of issuing a certificate is about $63.38 per certificate, then, a profit of $19.02 seems reasonable. Alternatively, the rate of return on such a transaction can be examined. A profit of $19.02 on a transaction that requires an investment of $63.38 over one year period translates into an annual rate of return of 30%.
The result in the paper provided additional evidence that structured products have been overpriced, 2% - 7% on average, in the primary market based on theoretical pricing models [1] -[29] for various types of structured products. The significant mispricing (30%) reported in this paper is especially in line with exotic certificates studied in the literature. Hernandez et al. [22] find that exotic cases of Bonus Certificates were overpriced 20% on average; Hernandez et al. [2] find that exotic cases of Japanese-Yen denominated Reverse Convertible Bonds were overpriced up to 30% on average, and Hernandez et al. [23] find that Protect Certificates were overpriced up to 19% on average.
5. Conclusion
In this paper a newly structured product known as cCSFS is introduced and detailed descriptions of the product specifications are provided. A pricing formula is developed to price the certificates. This paper shows that the payoff of a CSFS can be duplicated by the combination of a long position in put and call options with forward start on the underlying asset. A certificate issued by Credit Suisse is presented as an example to examine how well the model fits empirical data. The methodology used in this paper can be extended to the analysis of other structured products.
Acknowledgements
The authors wish to thank Dr. Pu Liu, Dr. Alexey Malakhov and the anonymous reviewers for their helpful comments.
References
- Das, S. (2001) Structured Products and Hybrid Securities. John Wiley & Sons Ltd., Singapore.
- Hernandez, R., Lee, W. and Liu, P. (2010) An Economic Analysis of the Japanese Reverse Exchangeable Market. Advances in Financial Planning and Forecasting 4, 159-191.
- Hernandez, R., Lee, W., Liu, P. and Dai, T. (2013) Outperformance Certificates: Analysis, Pricing, Interpretation, and Performance. Review of Quantitative Finance and Accounting, 40, 691-713. http://dx.doi.org/10.1007/s11156-012-0294-z
- Isakov, D. (2007) Le prix élevé de certains instruments tient aux frictions qui apparaissentsur le marché. Le Temps.
- Laise, E. (2006) An Arcane Investment Hits Main Street. Wall Street Journal (Eastern Edition), 247, D1-D3.
- Lyon, P. (2005) Editor’s Letter: The NASD Guidance Does Seem to Suggest That Structured Products Should Be the Preserve of the Privileged Few Who Are Eligible for Options Trading. Structured Products.
- Maxey, D. (2006) Market Builds for Structured Products. Wall Street Journal (Eastern Edition).
- National Association of Securities Dealer (2005) Notice to Members 05-59 Guidance Concerning the Sale of Structured Products. NASD, New York.
- Ricks, T. (1988) SEC Chief Calls Some Financial Products Too Dangerous’ for Individual Investors. Wall Street Journal, 1.
- Simmons, J. (2006) Derivatives Dynamo. Bloomberg Markets, 55-60.
- Rubinstein, M. (1991) Forward Start Options : Published as “Pay Now, Choose Later”. Risk Magazine, 4, 13.
- Hull, J. (2003) Options, Futures, and Other Derivatives. Pearson Education Inc., Upper Saddle River.
- Abken, P. (1989) A Survey and Analysis of Index-Linked Certificates of Deposit. Working Paper—Federal Reserve Bank of Atlanta, Atlanta, 89.
- Baubonis, C., Gastineau, G. and Purcell, D. (1993) The Banker’s Guide to Equity-Linked Certificates of Deposit. Journal of Derivatives, 1, 87-95. http://dx.doi.org/10.3905/jod.1993.407880
- Benet, B., Giannetti, A. and Pissaris, S. (2006) Gains from Structured Product Markets: The Case of Reverse-Exchangeable Securities (RES). Journal of Banking and Finance, 30, 111-132. http://dx.doi.org/10.1016/j.jbankfin.2005.01.008
- Black, F. and Scholes M. (1973) The Pricing of Options and Corporate Liabilities. Journal of Political Economy, 81, 637 -654. http://dx.doi.org/10.1086/260062
- Burth, S., Kraus, T. and Wohlwend, H. (2001) The Pricing of Structured Products in the Swiss Market. Journal of Derivatives, 9, 30-40. http://dx.doi.org/10.3905/jod.2001.319173
- Chance, D. and Broughton, J. (1988) Market Index Depository Liabilities. Journal of Financial Services Research, 1, 335-352. http://dx.doi.org/10.1007/BF00235203
- Chen, A. and Kensinger, J. (1990) An Analysis of Market-Index Certificates of Deposit. Journal of Financial Services Research, 4, 93-110. http://dx.doi.org/10.1007/BF00352565
- Chen, K. and Sears, R. (1990) Pricing the SPIN. Financial Management, 19, 36-47. http://dx.doi.org/10.2307/3665633
- Grünbichler, A. and Wohlwend, H. (2005) The Valuation of Structured Products: Empirical Findings for the Swiss Market. Financial Markets and Portfolio Management, 19, 361-380. http://dx.doi.org/10.1007/s11408-005-6457-3
- Hernandez, R., Brusa, J. and Liu, P. (2008) An Economic Analysis of Bonus Certificates—Second-Generation of Structured Products. Review of Futures Markets 16, 419-451.
- Hernandez, R., Jones, J. and Gu, Y. (2011) An Economic Analysis of Protect Certificates—An Option-Pricing Approach. Banking and Finance Review 3, 17-40.
- Hernandez, R., Lee, W. and Liu, P. (2010) An Economic Analysis of Reverse Exchangeable Securities—An Option-Pricing Approach. Review of Futures Markets, 19, 67-95.
- King, S. and Remolona, E. (1987) The Pricing and Hedging of Market Index Deposits. FRBNY Quarterly Review, 12, 9-20.
- Lyon, P. (2005) US Retail in the Firing Line. Structured Products.
- Merton, R .C. (1973) Theory of Rational Option Pricing. Bell Journal of Economics and Management Science, 4, 141- 183. http://dx.doi.org/10.2307/3003143
- Stoimenov, P. and Wilkens, S. (2005) Are Structured Products “Fairly” Priced? An Analysis of the German Market for Equity-Linked Instruments. Journal of Banking and Finance, 29, 2971-2993. http://dx.doi.org/10.1016/j.jbankfin.2004.11.001
- Wilkens, S., Erner, C. and Roder, K. (2003) The Pricing of Structured Products in Germany. The Journal of Derivatives, 11, 55-69. http://dx.doi.org/10.3905/jod.2003.319211
Appendix 1
Example of a Certificate on a Straddle with Future Start
The certificate in Appendix 1 was issued by investment bank Credit Suisse using the Nasdaq-100 Index as the underlying asset. The fixing date Credit Suisse set for the certificate was March 18, 2005 and the issue price of the certificate was $82.40 per certificate. The final fixing date was set on June 17, 2006.
Appendix 2
In this Appendix, we present the derivation of the pricing formulas for forward start European options with time to maturity T and that start at-the-money or proportionally inor out-of-the-money after a known elapsed time t in the future (Equations (4) and (8)) from Rubinstein [11] formulas. In Rubinstein [11] , the pricing formulas for forward start European call (cfs) and European put (pfs) options are:
 (A2-1)
(A2-1)
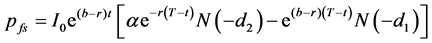 (A2-2)
(A2-2)
where
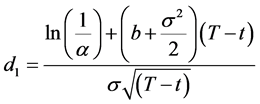 (A2-3)
(A2-3)
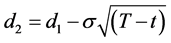 (A2-4)
(A2-4)
If we define b as the cost of carry rate (i.e. the cost of interest plus any additional costs) continuously compounded, the Black-Scholes [16] Merton [27] pricing model can be adapted to incorporate the cost-of-carry rate b and price European options on stocks or indices paying a continuous dividend yield. When b, the cost of carry rate, is set equal to the risk free interest rate, r, minus the continuous dividend yield rate of the underlying asset, q, the model gives the Merton [27] option pricing formulas with continuous dividend yield, q.
If we substitute b for (r − q) in Equations (A2-1), (A2-2), and (A2-3)
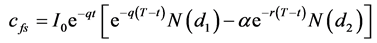 (A2-5)
(A2-5)
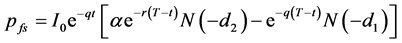 (A2-6)
(A2-6)
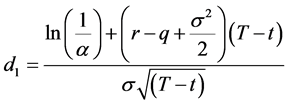 (A2-7)
(A2-7)
In the case of forward start European options, the strike price of the options is set equal to a positive constant, α, times the asset price It after the known time t. If α is set equal to one, the options will start at-the-money and Equations (A2-5), (A2-6), (A2-7), and (A2-4) are simplified and equal to Equations (4), (7), (5), and (6) respectively:
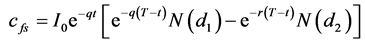
 (A2-8)
(A2-8)

 (A2-9)
(A2-9)
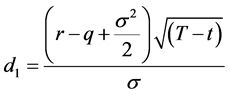 (A2-10)
(A2-10)
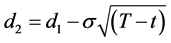 (A2-11)
(A2-11)
If we define T* as the time to maturity of the forward start European call options on the strike setting date t (i.e. T* = T − t), Equation (A2-8) is simplified to
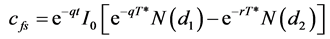
 (A2-12)
(A2-12)
where c is the value at time zero of an at-the-money European call option that lasts for T* and
 (A2-13)
(A2-13)
 (A2-14)
(A2-14)
If we define T* as the time to maturity of the forward start European put options on the strike setting date t (i.e. T* = T − t), Equation (A2-9) is simplified to
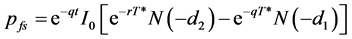
 (A2-15)
(A2-15)
where p is the value at time zero of an at-the-money European put option that lasts for T*, d1 as in Equation (A2-13), and d2 as in Equation (A2-14).
Appendix 3
In this Appendix, we present the approach we use calculating the equivalent continuous dividend yield rate for stocks that pay discrete dividends. For an underlying asset which is an individual stock with a price I0 at t = 0 (the issue date) and which pays n dividends during a time period T with cash dividend Di being paid at time ti, the equivalent dividend yield rate q will be such that
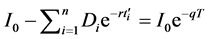
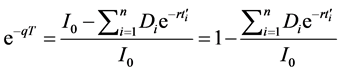
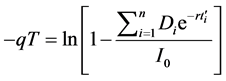

NOTES

1Forward start options are options with time to maturity T, starting at time t in the future with the strike price usually set equal to the underlying asset price at time t (i.e. at-the-money).

2,3See Appendix 2 for more details on the derivation of the formulas.


