Theoretical Economics Letters
Vol.4 No.4(2014), Article ID:45240,7 pages DOI:10.4236/tel.2014.44039
The Menu-Induced Core of an Economy with an Excludable Public Good
Toshiyuki Hirai
Faculty of Economics, University of Toyama, Toyama, Japan
Email: thirai@eco.u-toyama.ac.jp
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 1 February 2014; revised 5 March 2014; accepted 25 March 2014
Abstract
This paper introduces a core concept in an economy with an excludable public good. In the economy, we assume that each coalition is allowed to achieve an allocation via a menu, a kind of a nonlinear price. Our core concept is called the menu-induced core that is defined as the set of allocations achievable by menus that are robust against all coalitional improvements achieved via menus. We show that the menu-induced core is nonempty. We also investigate certain properties of the menu-induced core that show the difference between the menu-induced core and the core defined in a standard way.
Keywords
Menu-Induced Core, Excludable Public Good

1. Introduction
This paper examines economies with excludable public goods. The public goods that we consider are those that admit partial exclusion: the amount that each agent consumes may vary from agent to agent. Tollways, pay-per-view TV programs, and public transportation are traditional examples. More recent examples include online commodities such as music and movie downloading services and access rights to databases through the internet. The early researches on such commodities are, for example, Oakland [1] and Drèze [2] .
We consider stable allocations in cooperative decision situation of such an economy. In particular, we consider the core of the coalitional form of the economy. If we allow each coalition to achieve allocations with the individualized lump-sum payments, then the core essentially turns out to be that of Foley [3] . On the other hand, many examples of the excludable public goods are allocated through prices that may be nonlinear. For example, toll fare for the highway and a bundling sale of pay-per-view TV programs. According to this practice, we allow each coalition to achieve allocations via menus, which are a kind of nonlinear price.
A nonlinear price is a kind of system. In the literature, several authors considered the core of economies where each coalition is allowed to achieve an allocation via a given system. Guesnerie and Oddou [4] [5] considered the core of a pure public good economy where each coalition achieves an allocation via proportional income tax. Spulber [6] considered the core of a production economy with increasing returns to scale where each coalition achieves an allocation via the average cost price. Hara [7] [8] considered the exchange economies where allocations are achieved via menus. Indeed, our concept of the coalitional improvement and the core is an application of his menu-induced improvement and the anonymous core to the economy with an excludable public good.
To justify such a way to achieve an allocation, we implicitly assume the same informational constraint as Hara [7] [8] . He assumed that each agent knows the distribution of the characteristics of the agents, but cannot identify who has which characteristic. Under such an informational constraint, it is difficult for the agent to find appropriate members of a coalition and an appropriate allocation achieved in the coalition. In this situation, employing a menu for achieving an allocation is legitimate for revealing the characteristics of the agents.
Our core concept is defined as the menu-induced core. It is defined as the set of allocations satisfying the following two conditions: the allocation is achievable within the grand coalition via a menu; and no coalition can achieve an allocation via a menu that makes each agent in the coalition better off. We show the nonemptiness of the menu-induced core and observe some properties, which clarify the difference between the menu-induced core and the standard Foley’s core.
In the next section, we introduce the model of the economy with an excludable public good. In Section 3, we define the menu-induced core and prove its nonemptiness. Then, we investigate certain properties of the menu-induced core in Section 4. In the final section, we conclude with some remarks.
2. The Economy with an Excludable Public Good
We consider an economy consisting of ![]() agents, one private good, and one public good that is partially excludable. The set of agents is denoted by
agents, one private good, and one public good that is partially excludable. The set of agents is denoted by . A nonempty subset
. A nonempty subset ![]() of
of  is called a coalition. The set of all coalitions is denoted by
is called a coalition. The set of all coalitions is denoted by .
.
A typical consumption of 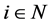 is denoted by
is denoted by , where
, where  and
and 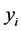 denote the amounts of the private good and the public good that
denote the amounts of the private good and the public good that 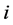 consumes, respectively. The preferences of each
consumes, respectively. The preferences of each 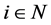 are represented by a utility function
are represented by a utility function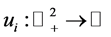 . For each
. For each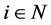 , it is assumed that
, it is assumed that 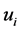 is continuous and monotone (i.e.,
is continuous and monotone (i.e., 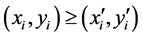 implies
implies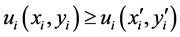 ). Each
). Each  is endowed with
is endowed with 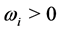 of the private good.
of the private good.
Each coalition can access to an identical production technology that transforms the private good into the public good. The production technology is represented by a cost function . It is assumed that
. It is assumed that ![]() is continuous, monotone (i.e.,
is continuous, monotone (i.e.,  implies
implies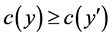 ),
),  , and
, and .
.
For each , an
, an ![]() -allocation is a tuple of the consumptions of agents in
-allocation is a tuple of the consumptions of agents in![]() . For each
. For each , an
, an ![]() allocation
allocation 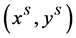 is said to be
is said to be ![]() -feasible iff
-feasible iff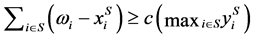 . Let
. Let 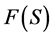 be the set of
be the set of ![]() feasible allocations for each
feasible allocations for each . An
. An 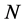 -allocation and an
-allocation and an  -feasible allocation are simply called an allocation and a feasible allocation, respectively. Given an allocation
-feasible allocation are simply called an allocation and a feasible allocation, respectively. Given an allocation , an
, an ![]() -allocation
-allocation 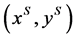 is said to be an improvement upon
is said to be an improvement upon 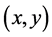 for
for ![]() iff
iff 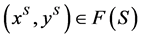 and
and  for all
for all .
.
Definition 1. An allocation  is in the standard core iff
is in the standard core iff 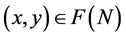 and there exists no
and there exists no  and
and 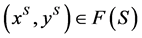 that is an improvement upon
that is an improvement upon .
.
Obviously, the standard core is essentially equivalent to that of Foley [3] for economies with pure public goods.
3. The Menu-Induced Core
This section introduces the main concepts of this paper, which are defined as an application of the similar concepts of Hara [7] [8] with slight modifications. Then, its nonemptiness is proved.
The menu is defined as a subset  of
of . It is a set of net consumptions:
. It is a set of net consumptions: 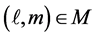 means that
means that  of the private good must be paid for consuming
of the private good must be paid for consuming ![]() of the public good. Thus, the resulting consumption of
of the public good. Thus, the resulting consumption of 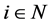 choosing
choosing  is
is .
.
For each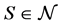 , let
, let 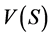 be a set of
be a set of ![]() -allocations such that
-allocations such that 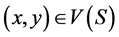 iff
iff 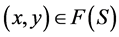 and there exists some
and there exists some  such that for all
such that for all , 1)
, 1) 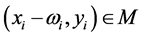 and 2)
and 2) 
implies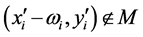 . A tuple
. A tuple 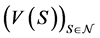 is called a menu-induced coalitional form of an economy.
is called a menu-induced coalitional form of an economy.
An allocation  is said to be menu-induced iff
is said to be menu-induced iff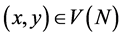 . This definition describes the situation as follows: once a menu is proposed, each agent chooses the most preferable net consumption from the proposed menu. The menu can be proposed by an agent who may find it by oneself or consulting with an outside intervener.
. This definition describes the situation as follows: once a menu is proposed, each agent chooses the most preferable net consumption from the proposed menu. The menu can be proposed by an agent who may find it by oneself or consulting with an outside intervener.
Given an allocation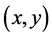 , a coalition
, a coalition ![]() has a menu-induced improvement upon
has a menu-induced improvement upon 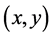 iff there exists some
iff there exists some 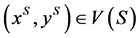 such that
such that 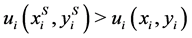 for all
for all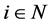 . The improvement by a menu describes the following situation. Given an allocation, an agent proposes a menu to agents in the economy. Again, the proposing agent may find it by oneself or consulting with an outside intervener. Then, each agent responds to the menu when one can make oneself better off by choosing the most preferable net consumption from the menu. The coalition is formed among the agents who respond to the proposed menu. One may notice that the definition of the menu-induced improvement does not take the behavior of the agents outside the coalition into account. The original definition of Hara [7] [8] described the behavior of the agents outside the coalition as follows: no agent outside the coalition finds it more preferable to choose a net consumption from the menu. Thus, we may also impose the following condition on the menu-induced improvement
. The improvement by a menu describes the following situation. Given an allocation, an agent proposes a menu to agents in the economy. Again, the proposing agent may find it by oneself or consulting with an outside intervener. Then, each agent responds to the menu when one can make oneself better off by choosing the most preferable net consumption from the menu. The coalition is formed among the agents who respond to the proposed menu. One may notice that the definition of the menu-induced improvement does not take the behavior of the agents outside the coalition into account. The original definition of Hara [7] [8] described the behavior of the agents outside the coalition as follows: no agent outside the coalition finds it more preferable to choose a net consumption from the menu. Thus, we may also impose the following condition on the menu-induced improvement 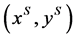 upon a given allocation
upon a given allocation  for
for![]() : for all
: for all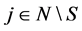 ,
,  for any
for any .
.
This condition is, however, redundant in our economy from the nonrivalry of the excludable public good. More precisely, for any allocation, there is a menu-induced improvement upon the allocation for  if and only if there is a
if and only if there is a ![]() -allocation with
-allocation with 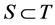 that satisfies both the definition of the menu-induced improvement and the additional condition. Therefore, imposing the additional condition does not change the nature of the menu-induced core that is defined below.
that satisfies both the definition of the menu-induced improvement and the additional condition. Therefore, imposing the additional condition does not change the nature of the menu-induced core that is defined below.
Definition 2. An allocation 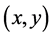 is said to be in the menu-induced core iff
is said to be in the menu-induced core iff  and there exist no
and there exist no  and
and  such that
such that 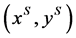 is a menu-induced improvement upon
is a menu-induced improvement upon 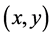 for
for![]() .
.
Now, we prove the nonemptiness of the menu-induced core.
Theorem 1. The menu-induced core is nonempty.
Proof. For any , define
, define
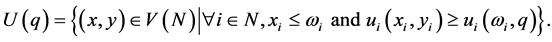
Further, define
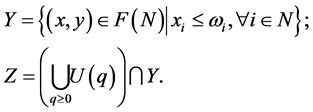
Clearly,  since
since . It can be easily confirmed that both
. It can be easily confirmed that both ![]() and
and 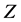 are compact sets by the assumptions of
are compact sets by the assumptions of 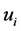 and
and![]() .
.
Define  for each
for each . Note that
. Note that  is a nonempty interval of
is a nonempty interval of 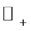 for any
for any 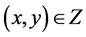 by definition.
by definition.
First, assume that there exists some  such that
such that 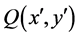 is unbounded above. Then, by the monotonicity of
is unbounded above. Then, by the monotonicity of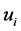 ,
,
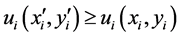 (1)
(1)
for all 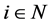 and any
and any  with
with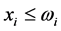 . We claim that
. We claim that  is in the menu-induced core.
is in the menu-induced core.
Suppose that there exist some 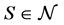 and a menu-induced improvement
and a menu-induced improvement 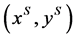 upon
upon  for
for![]() . Then,
. Then, 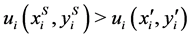 for all
for all . By (1), it must be
. By (1), it must be 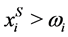 for all
for all . It follows that
. It follows that
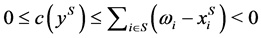 from the
from the ![]() -feasibility of
-feasibility of , a contradiction. Hence
, a contradiction. Hence 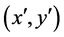 is in the menu-induced core.
is in the menu-induced core.
Next, assume that  is bounded for any
is bounded for any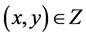 . We claim that
. We claim that 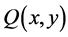 is closed for any
is closed for any . Fix an arbitrary
. Fix an arbitrary . Let
. Let  be a sequence taken from
be a sequence taken from 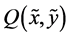 that converges to
that converges to . Then, we have
. Then, we have 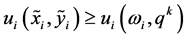 for all
for all 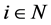 and for all
and for all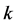 . It follows from the continuity of
. It follows from the continuity of  that
that  for all
for all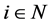 . Thus, in conjunction with the boundedness,
. Thus, in conjunction with the boundedness,  is a compact set for any
is a compact set for any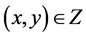 .
.
Thus, we can define  for any
for any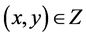 . We claim that
. We claim that 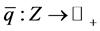 is an upper semi-continuous function. It suffices to show that
is an upper semi-continuous function. It suffices to show that  is closed for any
is closed for any
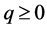 by the definition of
by the definition of![]() . Fix an arbitrary
. Fix an arbitrary . Let
. Let  be a sequence taken from
be a sequence taken from 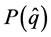 that converges to
that converges to . Then, we have
. Then, we have 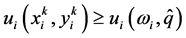 for all
for all  and for all
and for all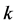 . It follows from the continuity of
. It follows from the continuity of 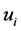 that
that 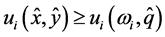 for all
for all . Thus,
. Thus,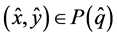 . Hence
. Hence ![]() is an upper semi-continuous function.
is an upper semi-continuous function.
Since 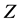 is a compact set and
is a compact set and  is an upper semi-continuous function, there exists some
is an upper semi-continuous function, there exists some 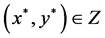 such that
such that 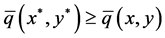 for any
for any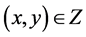 . We claim that
. We claim that 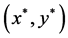 is in the menuinduced core.
is in the menuinduced core.
Let . Suppose that there exist some
. Suppose that there exist some  and a menu-induced improvement
and a menu-induced improvement  upon
upon 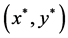 for
for![]() . By definition,
. By definition,  for all
for all . Define
. Define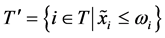 .
.
Then, . Thus,
. Thus, 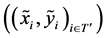 is still a menuinduced improvement upon
is still a menuinduced improvement upon  for
for 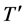 by its construction.
by its construction.
Then, 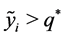 for all
for all 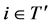 by the monotonicity of
by the monotonicity of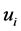 . Define
. Define
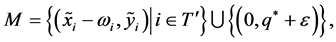
where 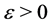 is a sufficiently small real number so that
is a sufficiently small real number so that 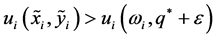 for all
for all . Define
. Define
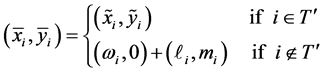
where  for each
for each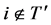 . Note that
. Note that  for all
for all  since
since  for all
for all 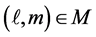 by its construction.
by its construction.
We confirm that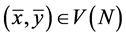 . The feasibility follows from
. The feasibility follows from  By the construction of
By the construction of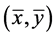 ,
, 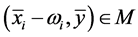 for all
for all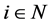 . By the definitions of
. By the definitions of  and
and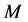 ,
, 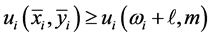 for any
for any  and all
and all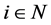 . Hence
. Hence . Moreover,
. Moreover,  since
since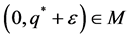 . Thus,
. Thus,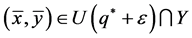 . This contradicts the definition of
. This contradicts the definition of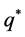 . Hence
. Hence 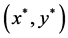 is in the menu-induced core.
is in the menu-induced core. 
Note that we require neither the quasi-concavity of the utility functions nor the convexity of the cost function.
Note also that the proof of Theorem 1 applies the idea of Mas-Colell [9] , which provides an alternative proof of a result of Champsaur [10] : the core of the coalitional game derived from an economy with one private good and one pure public good is nonempty. One may, therefore, consider that Theorem 1 is not surprising. However, the menu-induced core is generally much different from the standard core, which will be discussed in the next section.
4. Observations
In this section, we observe some properties of the menu-induced core, and discuss the difference from the standard core. One straightforward property from the definition is the symmetry of the allocations. Two agents  and
and  are symmetric iff
are symmetric iff  for any
for any 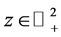 and
and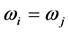 . An allocation
. An allocation  is symmetric iff
is symmetric iff 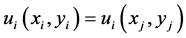 for any symmetric agents
for any symmetric agents 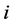 and
and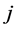 . It can be easily confirmed that any allocation in the standard core may not be symmetric.
. It can be easily confirmed that any allocation in the standard core may not be symmetric.
Property 1. Any allocation in the menu-induced core is symmetric.
The next property shows that the coalitional form of our economy may not satisfy the following usual property. The coalitional form of an economy 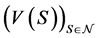 is said to be superadditive at
is said to be superadditive at  iff for all disjoint
iff for all disjoint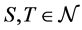 , for any
, for any 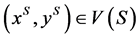 and any
and any , there exists some
, there exists some 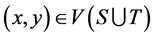 such that
such that  for all
for all 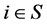 and
and  for all
for all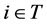 .
.
Property 2. 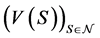 may not be superadditive at
may not be superadditive at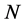 .
.
The following example shows Property 2.
Example 1. Let 
 . Let
. Let  for all
for all 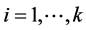 and
and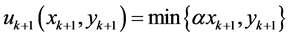 , where
, where  is sufficiently large. Let
is sufficiently large. Let  for all
for all 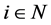 and
and . Clearly,
. Clearly, 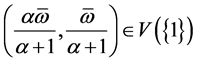 and
and . We have
. We have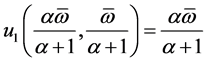 ,
,  for all
for all  and
and 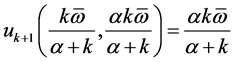 .
.
Let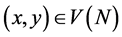 , induced by a menu
, induced by a menu , such that
, such that  and
and . Then,
. Then, 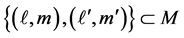 for some
for some 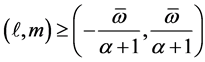 and some
and some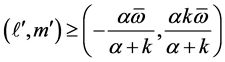 . Then, it must be
. Then, it must be 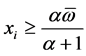 for each
for each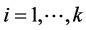 ,
,  and
and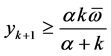 . Thus,
. Thus,
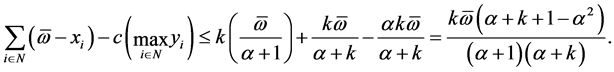 (2)
(2)
Thus, the most LHS of (2) is negative since ![]() is sufficiently large. In this case,
is sufficiently large. In this case, 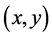 is not feasible. Hence the coalitional form of the economy may not be superadditive.
is not feasible. Hence the coalitional form of the economy may not be superadditive. 
Property 2 shows that our coalitional form is quite different from those in the literature. The coalitional form of an economy with one pure public good and one private good is known to be ordinary convex (see for example Peleg [11] for the definition of the ordinary convexity), which is a stronger condition than the superadditivity. See also Ichiishi [12] . On the other hand, Guesnerie and Oddou [4] [5] considered a coalitional form of an economy with one pure public good and one private good where each coalition is allowed to achieve an allocation through a proportional income tax. They showed that this coalitional form may not be superadditive and the core may be empty, while the menu-induced core is always nonempty in spite of the nonsuperadditivity.
The next property shows that there is a case where the menu-induced core is a subset of the standard core.
Property 3. If all agents are symmetric, then the menu-induced core is included in the standard core.
Proof. Assume that all agents are symmetric. Fix an arbitrary 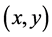 that is in the menu-induced core. For each
that is in the menu-induced core. For each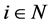 , define
, define 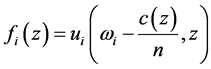 for any
for any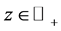 .
.
We claim that 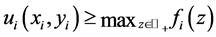 for all
for all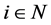 . Suppose that there exists some
. Suppose that there exists some  such that
such that . Then, by the symmetry of the agents,
. Then, by the symmetry of the agents, 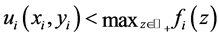 for all
for all . Let
. Let 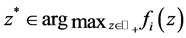 for all
for all . Note that such
. Note that such  exists by the symmetry of the agents. Then, we can easily confirm that
exists by the symmetry of the agents. Then, we can easily confirm that  where
where 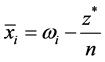 and
and  for all
for all  is a menu-induced improvement upon
is a menu-induced improvement upon . This contradicts that
. This contradicts that 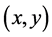 is in the menu-induced core. Hence
is in the menu-induced core. Hence 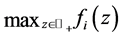
 for all
for all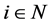 .
.
Then, we show that  is in the standard core. Suppose that there exist some
is in the standard core. Suppose that there exist some 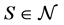 and an
and an ![]() - feasible allocation
- feasible allocation 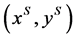 that is an improvement upon
that is an improvement upon 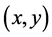 for
for![]() . Let
. Let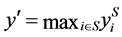 . Since
. Since 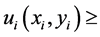
 for all
for all ,
,  for all
for all . Thus,
. Thus, 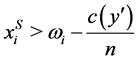 for all
for all . Then,
. Then, 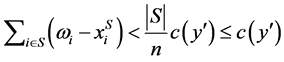 , contradicting that
, contradicting that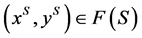 . Hecne
. Hecne 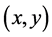 is in the standard core.
is in the standard core. 
On the other hand, there is a case where the menu-induced core is disjoint with the standard core.
Property 4. The intersection of the menu-induced core and the standard core may be empty.
The following example shows Property 4, which is a modification of an example in Guesnerie and Oddou [5] .
Example 2. Let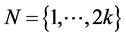 ,
, 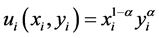 for
for 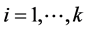 and
and  for
for  , where
, where , and
, and 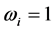 for all
for all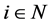 . The cost function is represented by
. The cost function is represented by .
.
At any allocation 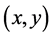 in the standard core, it can be easily confirmed that
in the standard core, it can be easily confirmed that 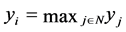 for all
for all  since the utility functions are continuous and strictly increasing in the interior of
since the utility functions are continuous and strictly increasing in the interior of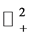 .
.
Let  be an allocation in the standard core. If
be an allocation in the standard core. If  is a menu-induced allocation, then it must be
is a menu-induced allocation, then it must be  for all
for all  since
since 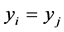 and
and 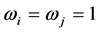 for all
for all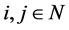 . Thus, there exists some
. Thus, there exists some 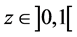 such that
such that 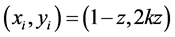 for all
for all .
.
Let us consider two menus  and
and . If at least
. If at least  agents prefer
agents prefer 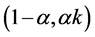 (
(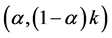 , respectively) to
, respectively) to , then
, then  is not in the menu-induced core. Thus, if
is not in the menu-induced core. Thus, if  is in the menu-induced core, it must be both
is in the menu-induced core, it must be both
 (3)
(3)
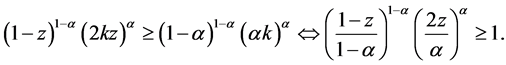 (4)
(4)
However, there exists no 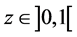 that simultaneously satisfies (3) and (4) if
that simultaneously satisfies (3) and (4) if ![]() is sufficiently small. Thus, in this example, the intersection of the standard core and the menu-induced core is empty.
is sufficiently small. Thus, in this example, the intersection of the standard core and the menu-induced core is empty. 
By Property 3 and 4, there is no general relationship between the menu-induced core and the standard core.
5. Concluding Remarks
This paper defined the menu-induced core and showed its nonemptiness in an economy with an excludable public good. We also discussed some properties of the menu-induced core. One remaining problem is the evaluation of the efficiency of the menu-induced core. In general, the menu-induced core fails to achieve the Pareto efficiency, which may be caused by the underlying informational constraints. We may consider the extent of the inefficiency, or efficiency evaluation under the similar informational constraints.
Another remaining problem is to design a mechanism that implements the allocations in the menu-induced core. In the economy with an excludable public good, some mechanisms are proposed. For example, Moulin [13] proposed the serial cost sharing mechanism, and Moldovanu [14] and Bag and Winter [15] proposed mechanisms that implement the standard core. However, all of them do not implement the menu-induced core. We leave these problems for future research.
Acknowledgements
I am grateful to an anonymous reviewer and Mikio Nakayama for their helpful comments and advices. I am also grateful for the financial supports by JSPS Grant-in-aid for Young Scientists (B) 22730155 and JSPS Grant-in-aid for Scientific Research (B) 24310110.
References
- Oakland, W. (1974) Public Goods, Perfect Competition, and Underproduction. Journal of Political Economy, 82, 927-939. http://dx.doi.org/10.1086/260247
- Drèze, J.H. (1980) Public Goods with Exclusion. Journal of Public Economics, 13, 5-24. http://dx.doi.org/10.1016/0047-2727(80)90020-1
- Foley, D. (1970) Lindahl’s Solution and the Core of an Economy with Public Goods. Econometrica, 38, 66-72. http://dx.doi.org/10.2307/1909241
- Guesnerie, R. and Oddou, C. (1979) On Economic Games Which Are Not Necessarily Superadditive. Economics Letters, 3, 301-306. http://dx.doi.org/10.1016/0165-1765(79)90001-6
- Guesnerie, R. and Oddou, C. (1981) Second-Best Taxation as a Game. Journal of Economic Theory, 25, 67-91. http://dx.doi.org/10.1016/0022-0531(81)90017-X
- Spulber, D.F. (1986) The Second Best Core. International Economic Review, 30, 623-631. http://dx.doi.org/10.2307/2526779
- Hara, C. (2002) The Anonymous Core of an Exchange Economy. Journal of Mathematical Economics, 38, 91-116. http://dx.doi.org/10.1016/S0304-4068(02)00066-6
- Hara, C. (2005) Bargaining Set and Anonymous Core without the Monotonicity Assumption. Journal of Mathematical Economics, 41, 545-556. http://dx.doi.org/10.1016/j.jmateco.2004.12.001
- Mas-Colell, A. (1980) Remarks on the Game-Theoretic Analysis of a Simple Distribution of Surplus Problem. International Journal of Game Theory, 9, 125-140. http://dx.doi.org/10.1007/BF01781368
- Champsaur, R.J. (1975) How to Share the Cost of a Public Good? International Journal of Game Theory, 4, 113-129. http://dx.doi.org/10.1007/BF01780629
- Peleg, B. (1986) A Proof That the Core of an Ordinal Convex Game Is a von Neumann-Morgenstern Solution. Mathematical Social Sciences, 11, 83-87. http://dx.doi.org/10.1016/0165-4896(86)90006-5
- Ichiishi, T. (1993) The Cooperative Nature of the Firm. Cambridge University Press, Cambridge.
- Moulin, H. (1994) Serial Cost Sharing of Excludable Public Goods. Review of Economic Studies, 61, 305-325. http://dx.doi.org/10.2307/2297983
- Moldovanu, B. (1996) The Production and Cost-Sharing of an Excludable Public Good. Economic Theory, 7, 531-539. http://dx.doi.org/10.1007/BF01213665
- Bag, P.K. and Winter, E. (1999) Simple Subscription Mechanisms for Excludable Public Goods. Journal of Economic Theory, 87, 72-94. http://dx.doi.org/10.1006/jeth.1998.2497

