Theoretical Economics Letters
Vol. 3 No. 3A (2013) , Article ID: 33211 , 7 pages DOI:10.4236/tel.2013.33A004
The Ambivalent Role of Idiosyncratic Risk in Asymmetric Tournaments
1School of Economics and Business, Eberhard Karls University Tuebingen, Tuebingen, Germany
2Mathematics, Eberhard Karls University Tuebingen, Tuebingen, Germany
3Department of Economics, University of Warwick, Coventry, UK
Email: kerstin.pull@uni-tuebingen.de, hendrik.baeker@uni-tuebingen.de, agnes.baeker@uni-tuebingen.de
Copyright © 2013 Kerstin Pull et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 23, 2013; revised April 24, 2013; accepted May 24, 2013
Keywords: Tournaments; Contestant Heterogeneity; Idiosyncratic Risk
ABSTRACT
In our paper, we analyze the interplay of contestant heterogeneity and idiosyncratic risk in rank-order tournaments: While in symmetric tournaments an increase in idiosyncratic risk reduces incentives, in asymmetric tournaments this is not necessarily the case: Rather, we show that increasing the level of idiosyncratic risk in asymmetric tournaments will at first increase and—only after a critical risk level has been reached—reduce incentives. We find this critical risk level to be higher, the larger the degree of contestant heterogeneity. Concerning practical implications, it is more important to reduce idiosyncratic risk in the tournament when contestants are similar and less beneficial when contestants are heterogeneous. In light of the fact that equilibrium effort levels in tournaments with a low level of contestant heterogeneity are by far higher than those in tournaments with high levels of contestant heterogeneity, the advice would be to simultaneously reduce contestant heterogeneity (e.g., by league-building or handicapping) and idiosyncratic risk.
1. Introduction
Tournament incentives have developed into an important component of organizational reward systems: Employees compete against one another with the best performing employee(s) receiving a predefined tournament prize (e.g. a promotion, a bonus payment, a travel incentive or the like). Given the prevalence of tournament incentives, it is not surprising that beginning with the seminal paper by [1] the incentive properties of tournaments have repeatedly been analyzed (e.g. [2]).
In our paper, we analyze the effect of idiosyncratic, i.e. contestant-specific, risk in a tournament where contestants are heterogeneous. While the literature has regarded the effects of both idiosyncratic risk and contestant heterogeneity in isolation, the interplay of the two has not received much attention yet.
Starting first with contestant heterogeneity, this refers to a situation where contestants in a tournament are not equally talented in doing their job. In a two-person tournament, e.g., where one of the two contestants is of much higher ability, both contestants will not be inclined to put in much effort in the tournament—knowing that the more talented one will win anyway. Consequently, tournament incentives are distorted in a situation where contestants are heterogeneous (see, e.g. [1]).
Concerning risks, it is important to distinguish between two different types of risk: common risks on the one hand and idiosyncratic risks on the other. While the former affect the output of all contestants alike (e.g. seasonal fluctuations or fluctuations over the business cycle), the latter are contestant-specific and are not leveled out by the tournament. From the literature it is clear that if contestants are homogenous (symmetric tournament), an increase in idiosyncratic risk will decrease tournament incentives as the expected marginal return of an increased effort level is reduced. However, if and how an increase in idiosyncratic risk will affect tournament incentives in an asymmetric tournament, i.e., in a tournament that is characterized by contestant heterogeneity, is far less clear and has not been explored so far. This is despite the fact that in reality we will typically observe both, contestant heterogeneity and idiosyncratic risks, at the same time.
In the recent literature on asymmetric tournaments (e.g. [3]), only [4,5] are concerned with the role of idiosyncratic risk. However, other than in this paper, [4] as well as [5] are interested in agents’ active risk-taking strategies and model risk as a second choice variable of contestants1. To the contrary, in our paper we are concerned with exogenously determined idiosyncratic risks which are inherent in almost any production or measurement technology. Further, and on a more technical note, our paper differs from the one by [4] in that [4] vary the degree of heterogeneity for two distinct levels of risk, whereas we vary the level of idiosyncratic risk— given the level of heterogeneity. While [4] as well as [5] find that in a situation with a low degree of contestant heterogeneity, an (endogenous) increase in idiosyncratic risk will generally reduce tournament incentives, in our framework this is no longer the case: An exogenous increase in the amount of idiosyncratic risk in an asymmetric tournament starting from an initially very low level of risk will rather at first increase tournament incentives and only later on (after a critical level of idiosyncratic risk has been reached) reduce these.
The intuition of this ambivalent effect is as follows: At very low levels of risk inherent in the production technology, even a small degree of (publicly known) contestant heterogeneity is apt to distort tournament incentives as the outcome of the tournament becomes more or less predictable: The more able contestant will know that even a low level of effort will make her win the tournament, and hence the best response of the less able contestant will be to choose a low level of effort as well. In such a situation, an increase in the amount of idiosyncratic risk will reduce the predictability of the outcome and will therefore make it more worthwhile for the two contestants to exert high effort levels. However, when a certain critical level of idiosyncratic risk has been reached, a further increase in risk will decrease incentives again—just as it is the case in symmetric tournaments, i.e., as long as idiosyncratic risks do not fully compensate for contestant heterogeneity, adding more risk to the contest will increase incentives; as soon as idiosyncratic risks more than compensate for contestant heterogeneity, adding more risk will decrease incentives.
The level of idiosyncratic risk where the positive relation between risk and tournament incentives turns into a negative one depends on the degree of contestant heterogeneity: The smaller the degree of contestant heterogeneity, the lower the critical risk level, i.e., the smaller the range of risk levels where the effect of an increase in risk on equilibrium effort is positive. Hence, provided that contestant heterogeneity is sufficiently low, an increase in idiosyncratic risk will decrease tournament incentives over wide ranges of the risk spectrum. For higher degrees of contestant heterogeneity, however, this is no longer true: Over a large range of the risk spectrum, an increase in idiosyncratic risk will rather increase tournament incentives.
The remainder of this paper is organized as follows: Section 2 starts with a reference model with two homogeneous contestants and then introduces heterogeneity on the part of contestants. Section 3 presents a short discussion and practical implications, Section 4 concludes.
2. The Model
In a first reference case, let there be two homogeneous employees  who compete in a rank-order tournament. Both employees independently choose an effort level
who compete in a rank-order tournament. Both employees independently choose an effort level![]() , which is not observable and only known to the respective employee. Individual output
, which is not observable and only known to the respective employee. Individual output  is assumed to be observable and is a function of effort level
is assumed to be observable and is a function of effort level ![]() and an idiosyncratic error term
and an idiosyncratic error term 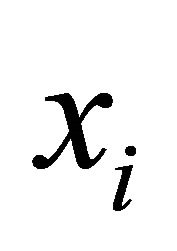 with
with . The idiosyncratic error terms
. The idiosyncratic error terms 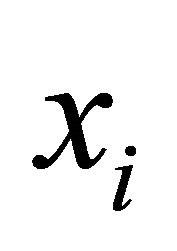 are assumed to be identically and independently distributed with
are assumed to be identically and independently distributed with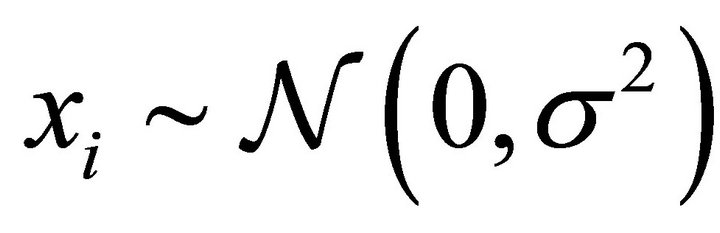 . The tournament foresees that employee
. The tournament foresees that employee  is awarded the tournament prize
is awarded the tournament prize  if
if . When choosing his or her effort level, each of the risk-neutral employees
. When choosing his or her effort level, each of the risk-neutral employees  individually maximizes his or her expected utility:
individually maximizes his or her expected utility:
 (1)
(1)
where 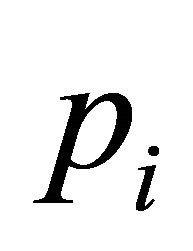 denotes the probability of winning the tournament for employee
denotes the probability of winning the tournament for employee  and where
and where  denotes the costs of effort with
denotes the costs of effort with  and
and .
.
The probability 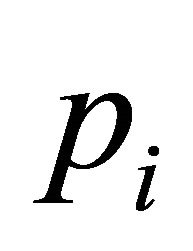 of winning the tournament is given by:
of winning the tournament is given by:
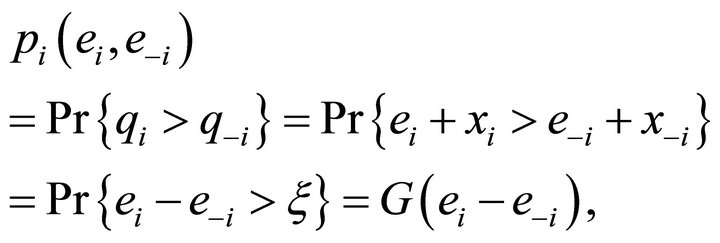 (2)
(2)
where ![]() is the composed error term
is the composed error term 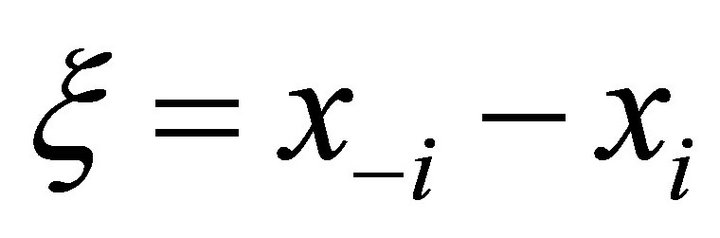 and where
and where  denotes its cumulated distribution function. The composed error term
denotes its cumulated distribution function. The composed error term ![]() is normally distributed with
is normally distributed with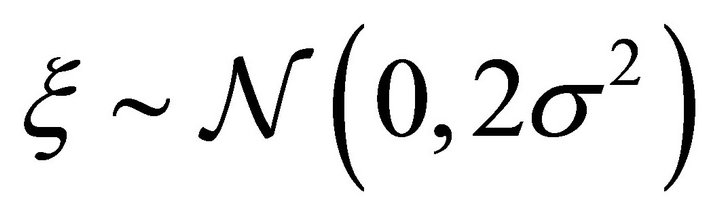 . Solving the maximization problem in Equation (1) and substituting for
. Solving the maximization problem in Equation (1) and substituting for  according to Equation (2), one arrives at the following reaction function for employee
according to Equation (2), one arrives at the following reaction function for employee :
:
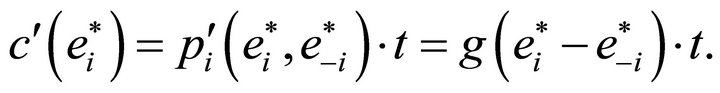 (3)
(3)
Hence, we arrive at the well-known result that each employee will choose an effort level such that his or her marginal costs of effort 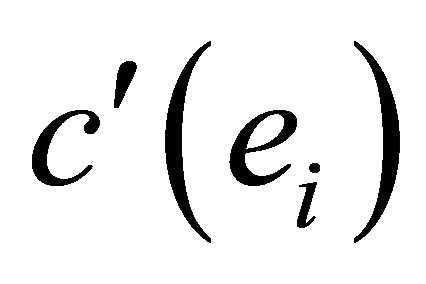 are equal to his or her marginal returns in form of an increased chance of winning the tournament
are equal to his or her marginal returns in form of an increased chance of winning the tournament  multiplied by the tournament prize
multiplied by the tournament prize , where
, where 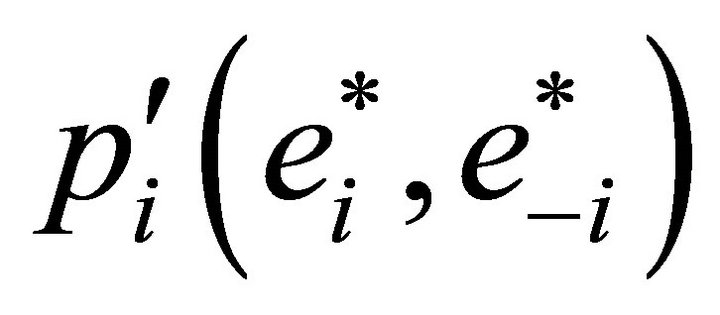 may be written in terms of the density function of the composed error term evaluated at
may be written in terms of the density function of the composed error term evaluated at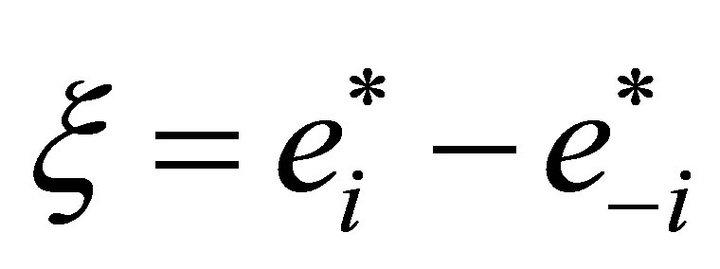 . Symmetry of
. Symmetry of 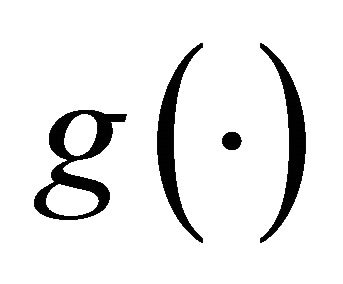 implies that, if a Nash-equilibrium in pure strategies exists2, we have
implies that, if a Nash-equilibrium in pure strategies exists2, we have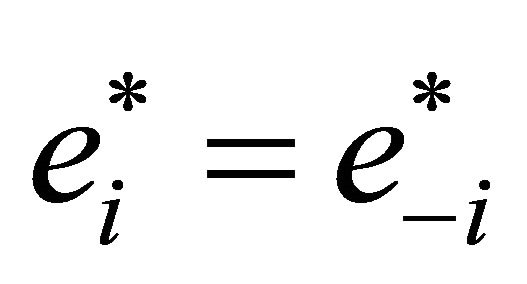 . Hence, Equation (3) can be re-written as:
. Hence, Equation (3) can be re-written as:

Concerning the impact of idiosyncratic risk on tournament incentives, a higher amount of risk (i.e., a lower value of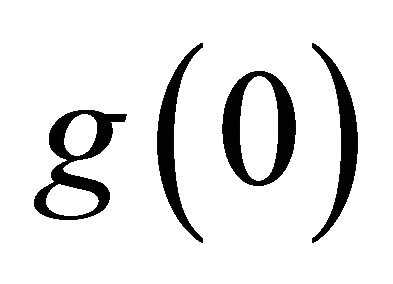 ), will generally decrease effort levels in a symmetric tournament.
), will generally decrease effort levels in a symmetric tournament.
Example 2.1. The following example—which will prove to be useful in the case of heterogeneous contestants— may illustrate this effect: Assuming quadratic effort costs with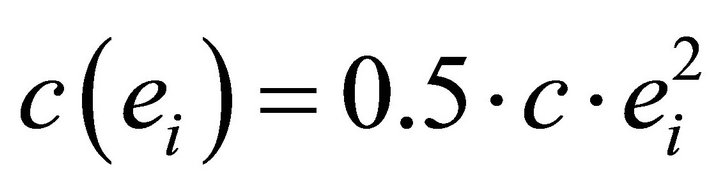 , the equilibrium effort level
, the equilibrium effort level 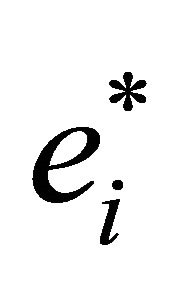 is given by:
is given by:

Hence, an increase in idiosyncratic risk as indicated by a larger ![]() will decrease equilibrium effort.
will decrease equilibrium effort.
In what follows, heterogeneity on the part of employees is introduced. In accordance with [1] and with e.g. [5,8,9], we do so by assuming that employees vary in their marginal costs of effort3. Again let ![]() denote the effort level and
denote the effort level and  the costs of effort of contestant
the costs of effort of contestant . Let employee 1 be characterized by generally lower marginal costs of effort than employee 2, i.e. assume that
. Let employee 1 be characterized by generally lower marginal costs of effort than employee 2, i.e. assume that  holds for all effort levels
holds for all effort levels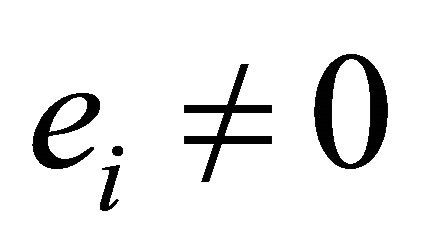 . When no effort is displayed, there are zero costs
. When no effort is displayed, there are zero costs 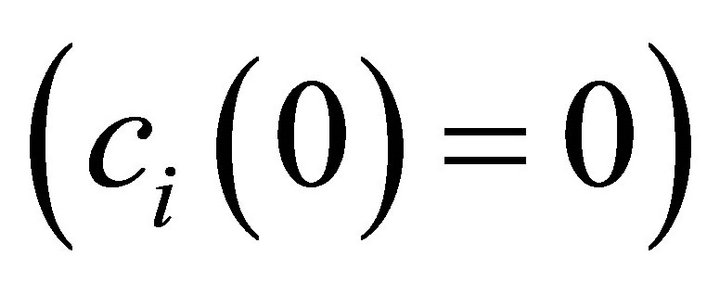 and also marginal costs are set to zero
and also marginal costs are set to zero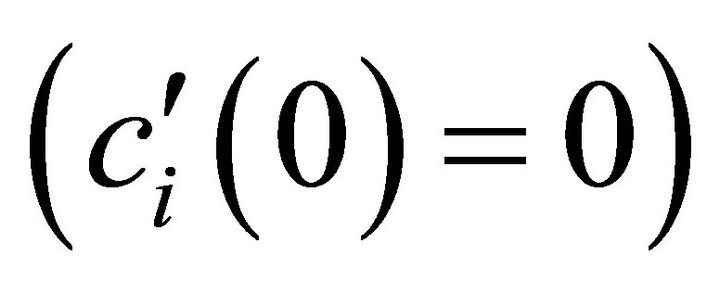 . Furthermore and for technical reasons we assume that for the second derivatives we have
. Furthermore and for technical reasons we assume that for the second derivatives we have 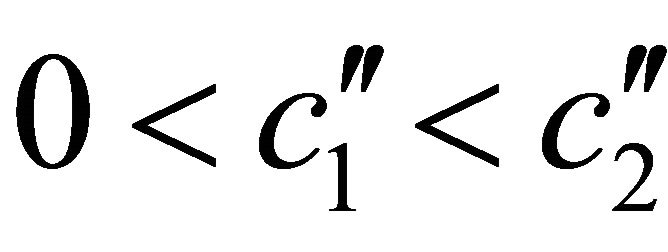 and that
and that  holds. In a Nash-equilibrium, the reaction function of employee
holds. In a Nash-equilibrium, the reaction function of employee  will then take the following form:
will then take the following form:
 (4)
(4)
Since 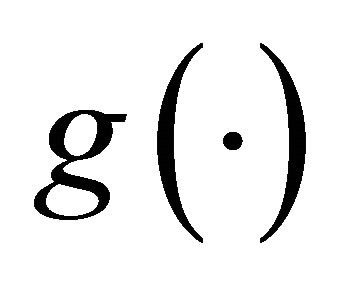 is symmetric,
is symmetric, 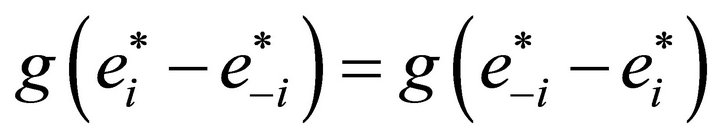 holds. Hence, with
holds. Hence, with 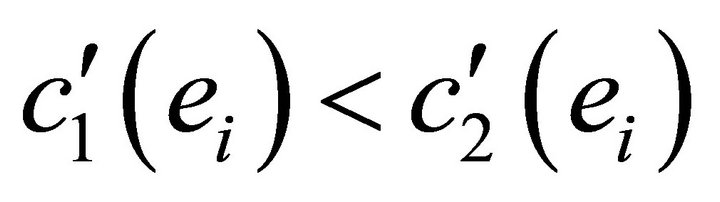 for all effort levels
for all effort levels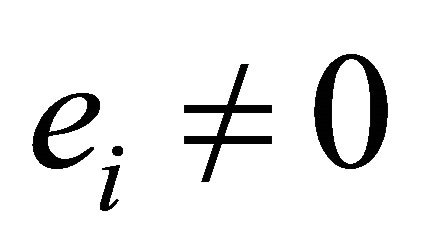 , in equilibrium employee 1 will choose a higher effort level than employee 2:
, in equilibrium employee 1 will choose a higher effort level than employee 2: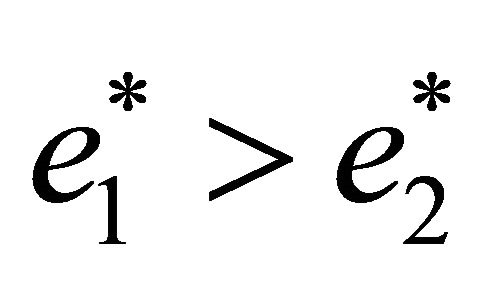 . As
. As 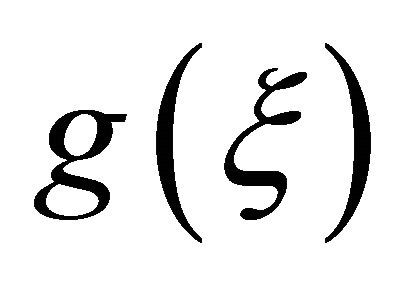 displays a maximum at
displays a maximum at 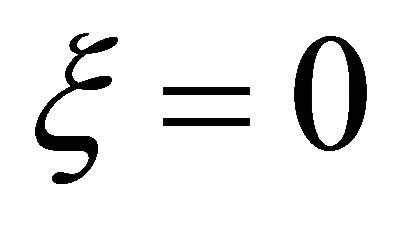 (see Figure 1), we can further write:
(see Figure 1), we can further write:
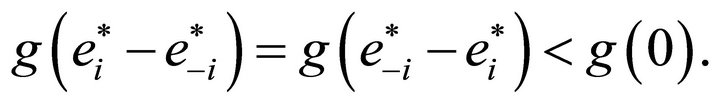 (5)
(5)
Thus, in an asymmetric tournament, for a given tournament prize , both employees will choose lower effort levels than each of them would have chosen in a symmetric tournament. The intuition for this effect is straight forward: For each of the employees, the marginal revenue of choosing a higher effort level (as is being represented by an increase in the probability of winning the tournament multiplied by the tournament prize) is reduced in an asymmetric as compared to a symmetric tournament where the ex ante [and ex post] chances to win the tournament are identical for the two contestants. The larger the ability differentials, i.e., the larger the degree of contestant heterogeneity, the lower the incentives to provide effort (for given levels of idiosyncratic risk).
, both employees will choose lower effort levels than each of them would have chosen in a symmetric tournament. The intuition for this effect is straight forward: For each of the employees, the marginal revenue of choosing a higher effort level (as is being represented by an increase in the probability of winning the tournament multiplied by the tournament prize) is reduced in an asymmetric as compared to a symmetric tournament where the ex ante [and ex post] chances to win the tournament are identical for the two contestants. The larger the ability differentials, i.e., the larger the degree of contestant heterogeneity, the lower the incentives to provide effort (for given levels of idiosyncratic risk).
Concerning the effect of idiosyncratic risk on effort levels, however, the picture is less clear: Tournament incentives may in fact either increase or decrease with the level of idiosyncratic risk—depending on the (endogenously to be determined) difference in equilibrium effort levels.
Example 2.2. Recurring on the above example and assuming quadratic effort costs for both contestants with
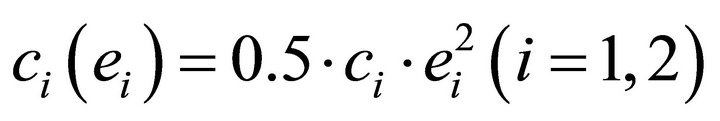 yields that we have
yields that we have 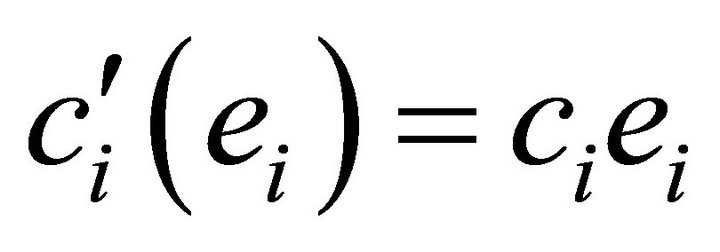 giving us
giving us 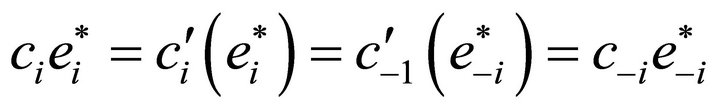 and hence we obtain:
and hence we obtain:
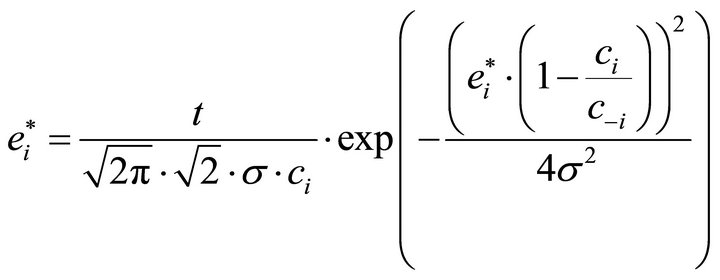
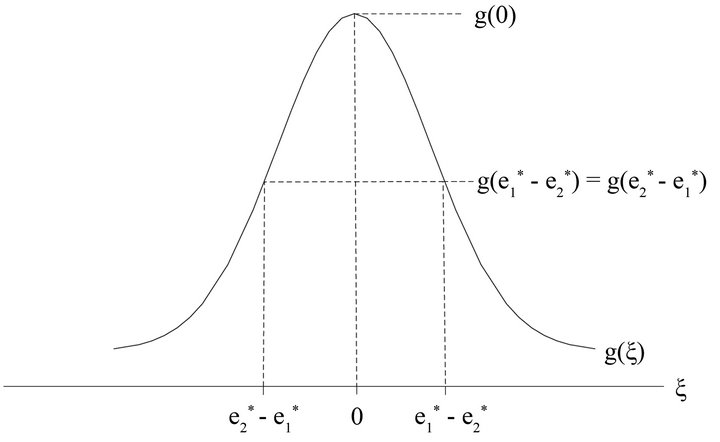
Figure 1. Idiosyncratic risk and equilibrium effort levels.
Figure 2 plots the equilibrium effort level of contestant  as a function of the level of idiosyncratic risk as measured by
as a function of the level of idiosyncratic risk as measured by ![]() for the parameters
for the parameters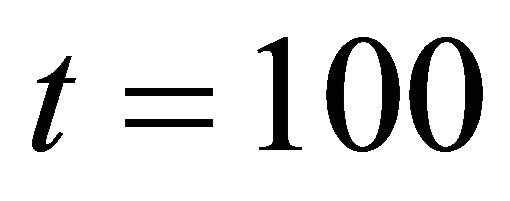 ,
, 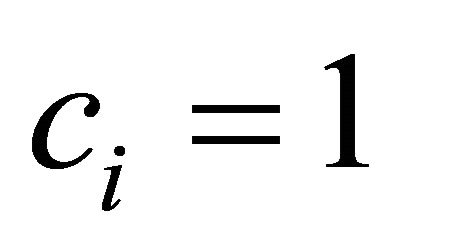 and
and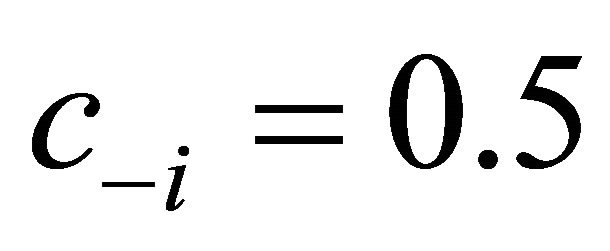 .
.
As Figure 2 shows, an increase in idiosyncratic risk will at first increase incentives and then reduce them. The intuition for this effect is as follows: At very low levels of idiosyncratic risk4, contestant heterogeneity will adversely affect effort levels. Adding risk to the contest 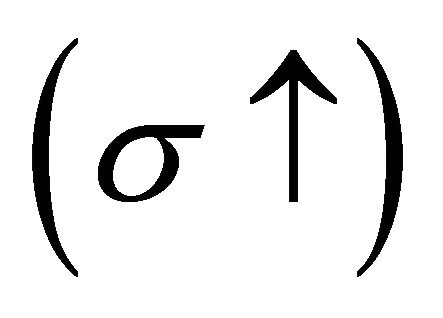 will reduce the predictability of the outcome, increase the marginal return of exerting higher effort levels for the two contestants and will hence make it more worthwhile for the contestants to exert positive effort levels. However, when a critical level of risk
will reduce the predictability of the outcome, increase the marginal return of exerting higher effort levels for the two contestants and will hence make it more worthwhile for the contestants to exert positive effort levels. However, when a critical level of risk  is reached, a further increase in risk will decrease incentives again—just as it is the case in symmetric contests, i.e., as long as idiosyncratic risks do not fully compensate for contestant heterogeneity, adding more risk to the contest will increase incentives; as soon as idiosyncratic risks more than compensate for contestant heterogeneity, adding more risk will decrease incentives. This is equivalent to stating that the function for
is reached, a further increase in risk will decrease incentives again—just as it is the case in symmetric contests, i.e., as long as idiosyncratic risks do not fully compensate for contestant heterogeneity, adding more risk to the contest will increase incentives; as soon as idiosyncratic risks more than compensate for contestant heterogeneity, adding more risk will decrease incentives. This is equivalent to stating that the function for  displays a maximum in the idiosyncratic risks
displays a maximum in the idiosyncratic risks ![]() where
where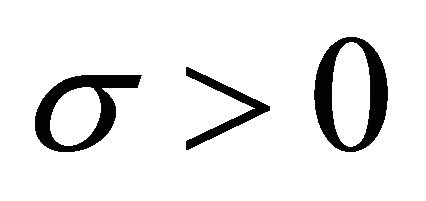 . This maximum is displayed at the critical risk level
. This maximum is displayed at the critical risk level . We obtain:
. We obtain:
Theorem 2.3. There is a unique risk level 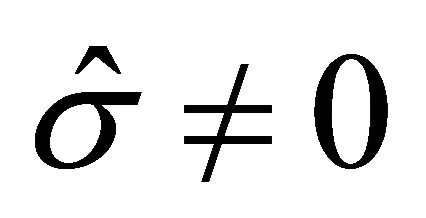 for which
for which  are simultaneously maximal and for this level the following equation holds:
are simultaneously maximal and for this level the following equation holds:

Proof. See Appendix.
The theorem gives us an equation for the level of risk in the tournament at which the effort of both contestants is at a maximum. This equation does not depend on the effort levels; unfortunately, however, it is an implicit formula. As we will see in the following Example 2.4, when choosing suitable cost functions we can compute an explicit value for the optimal risk level which only depends on contestant heterogeneity.
Example 2.4. Assuming the same cost functions as in 2.2 Theorem 2.3 yields an explicit formula for the critical risk level :
:

where the first factor can be interpreted as heterogeneity
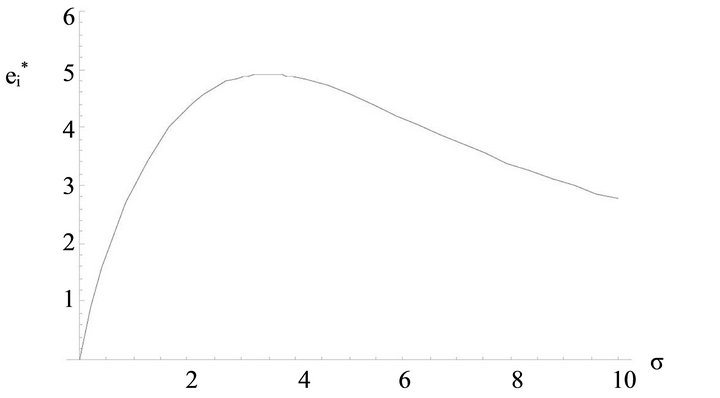
Figure 2. Idiosyncratic risk and equilibrium effort levels in an asymmetric tournament.
of the contestants.
The critical risk level  at which the positive effect of idiosyncratic risk on tournament incentives turns into a negative one, depends on the degree of contestant heterogeneity with a higher degree of contestant heterogeneity leading to a higher critical risk level.
at which the positive effect of idiosyncratic risk on tournament incentives turns into a negative one, depends on the degree of contestant heterogeneity with a higher degree of contestant heterogeneity leading to a higher critical risk level.
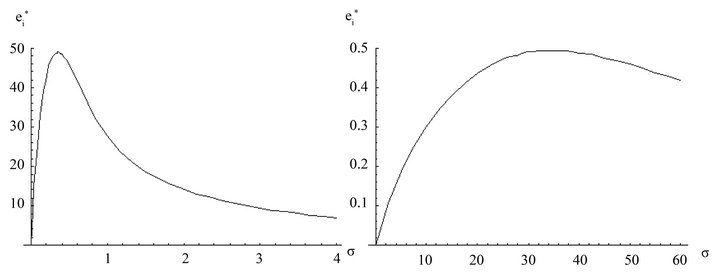
Figure 3 plots the equilibrium effort level of contestant  as a function of the level of idiosyncratic risk as measured by
as a function of the level of idiosyncratic risk as measured by ![]() for (a) a situation where contestants are almost homogeneous in their marginal effort costs and (b) a situation where the degree of contestant heterogeneity is rather large5. If the differential in marginal effort costs is low (Figure 3(a)), the critical risk value beyond which the positive effect on incentives turns into a negative one is reached at a lower risk level than if the differential in marginal effort costs is high (Figure 3(b)). Hence, for a low level of contestant heterogeneity an increase in risk will decrease incentives over a wide range of the risk spectrum (just as is the case in a symmetric tournament) while for a high level of contestant heterogeneity an increase in risk will increase incentives over a wide range of the risk spectrum.
for (a) a situation where contestants are almost homogeneous in their marginal effort costs and (b) a situation where the degree of contestant heterogeneity is rather large5. If the differential in marginal effort costs is low (Figure 3(a)), the critical risk value beyond which the positive effect on incentives turns into a negative one is reached at a lower risk level than if the differential in marginal effort costs is high (Figure 3(b)). Hence, for a low level of contestant heterogeneity an increase in risk will decrease incentives over a wide range of the risk spectrum (just as is the case in a symmetric tournament) while for a high level of contestant heterogeneity an increase in risk will increase incentives over a wide range of the risk spectrum.
3. Discussion
Unlike [4]—and, similarly, [5]—we find that when risk is not a choice variable, but rather inherent to the production process, introducing risk into an asymmetric tournament will always at first increase equilibrium effort levels and then decrease them—irrespective of the size of the ability differential.
Note, however, that the equilibrium effort levels chosen in a situation with a low degree of contestant heterogeneity are by far higher than those in a situation with a high degree of contestant heterogeneity. The results concerning a high degree of contestant heterogeneity are well in line with the suppositions of [11] and [12] who each postulate that increasing the risk in a contest
 (a) (b)
(a) (b)
Figure 3. Idiosyncratic risk and equilibrium effort levels in more or less uneven tournaments. (a) Low degree of contestant heterogeneity; (b) High degree of contestant heterogeneity.
(through less monitoring by the tournament sponsor) might in fact lead to higher effort levels by all contestants.
With respect to practical implications, our analysis shows that it is more important to invest in a decrease of idiosyncratic risk (e.g., by reducing measurement error) in tournament compensation systems when contestants are similar in their effort costs (low level of contestant heterogeneity). The more heterogeneous contestants are, the less beneficial (if not even costly) are these attempts. In light of the fact that equilibrium effort levels in tournaments with a low level of contestant heterogeneity are by far higher than those in tournaments with high levels of contestant heterogeneity, the practical advice would be to simultaneously reduce contestant heterogeneity (e.g., by league-building or handicapping) and idiosyncratic risk.
4. Conclusion
We show that an increasing amount of idiosyncratic risk does not generally decrease incentives when contestants are heterogeneous. Rather, an increase in idiosyncratic risk will first increase incentives in an asymmetric tournament and will only start to decrease incentives after some—critical—risk level has been reached. This critical risk level—in turn—depends on the degree of contestant heterogeneity: The lower contestant heterogeneity, the lower is the critical risk level: i.e., for very low levels of contestant heterogeneity, an increase in idiosyncratic risk will decrease tournament incentives over a wide range of the risk spectrum while for high levels of contestant heterogeneity, increasing the amount of risk in the contest will increase tournament incentives over a wide range of the risk spectrum.
5. Acknowledgements
The authors would like to thank Matthias Kräkel and Dirk Sliwka for helpful comments and suggestions.
REFERENCES
- E. P. Lazear and S. Rosen, “Rank-Order Tournaments as Optimum Labor Contracts,” Journal of Political Economy, Vol. 89, No. 5, 1981, pp. 841-864. doi:10.1086/261010
- B. E. Becker and M. A. Huselid, “The Incentive Effects of Tournament Compensation Systems,” Administrative Science Quarterly, Vol. 37, No. 2, 1992, pp. 336-350. doi:10.2307/2393228
- C. Harbring and G. K. Lünser, “On the Competition of Asymmetric Agents,” German Economic Review, Vol. 9, No. 3, 2008, pp. 373-395. doi:10.1111/j.1468-0475.2008.00438.x
- M. Kräkel and D. Sliwka, “Risk Taking in Asymmetric Tournaments,” German Economic Review, Vol. 5, No. 1, 2004, pp. 103-116. doi:10.1111/j.1465-6485.2004.00096.x
- M. Kräkel, “Optimal Risk Taking in an Uneven Tournament Game with Risk Averse Players,” Journal of Mathematical Economics, Vol. 44, No. 11, 2008, pp. 1219-1231. doi:10.1016/j.jmateco.2008.02.002
- P. Nieken and D. Sliwka, “Risk-Taking Tournaments: Theory and Experimental Evidence,” Journal of Economic Psychology, Vol. 31, No. 3, 2010, pp. 254-268. doi:10.1016/j.joep.2009.03.009
- P. Nieken, “On the Choice of Risk and Effort in Tournaments-Experimental Evidence,” Journal of Economics and Management Strategy, Vol. 19, No. 3, 2010, pp. 811-840. doi:10.1111/j.1530-9134.2010.00270.x
- C. Bull, A. Schotter and K. Weigelt, “Tournaments and Piece Rates: An Experimental Study,” Journal of Political Economy, Vol. 95, No. 1, 1987, pp. 1-33. doi:10.1086/261439
- K. J. McLaughlin, “Aspects of Tournament Models: A Survey,” Research in Labor Economics, Vol. 9, No. 1, 1988, pp. 225-256.
- M. O’Keefe, W. K. Viscusi and R. J. Zeckhauser, “Economic Contests: Comparative Reward Schemes,” Journal of Labor Economics, Vol. 2, No. 1, 1984, pp. 27-56. doi:10.1086/298022
- T. Cowen and A. Glazer, “More Monitoring Can Induce Less Effort,” Journal of Economic Behavior & Organisation, Vol. 30, No. 1, 1996, pp. 113-123. doi:10.1016/S0167-2681(96)00845-1
- P. Dubey and C. Wu, “Competitive prizes: When less Scrutiny Induces More Effort,” Journal of Mathematical Economics, Vol. 36, No. 4, 2001, pp. 311-336. doi:10.1016/S0304-4068(01)00079-9
Appendix: Proof of Theorem 2.3
Let us recall some of the notation used. By ![]() we denote the effort level and by
we denote the effort level and by ![]() the costs of effort of contestant
the costs of effort of contestant . In a Nash-equilibrium we then obtain
. In a Nash-equilibrium we then obtain
 (6)
(6)
where by  we denote the equilibrium effort levels. Symmetry of
we denote the equilibrium effort levels. Symmetry of ![]() yields
yields
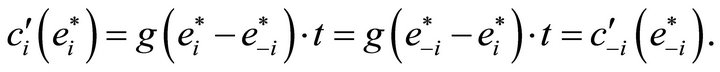 (7)
(7)
We now assume  and
and  to vanish; contestant heterogeneity is modeled by
to vanish; contestant heterogeneity is modeled by 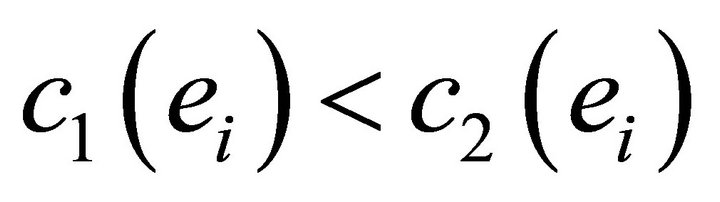 for every level
for every level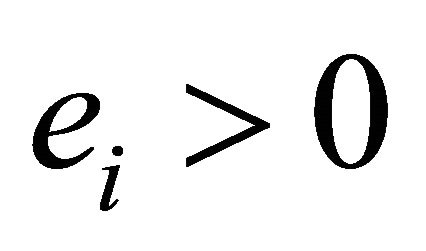 . Furthermore for the second derivatives
. Furthermore for the second derivatives 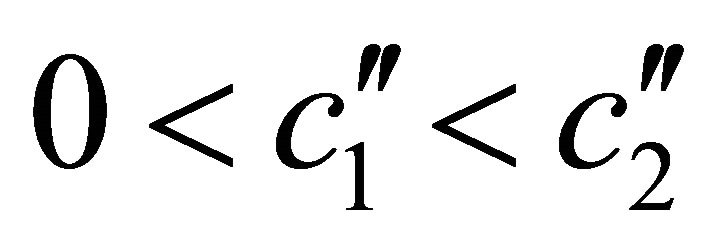 shall hold. This means
shall hold. This means  is strictly increasing, i.e. the inverse function
is strictly increasing, i.e. the inverse function 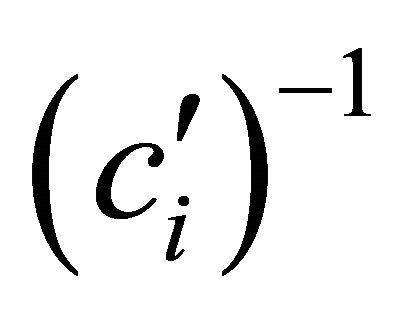 exists. Further, we assume that
exists. Further, we assume that  holds.
holds.
For the sake of simplifying the calculation we fix some more notation and do some technical preparations. Let ![]() and
and
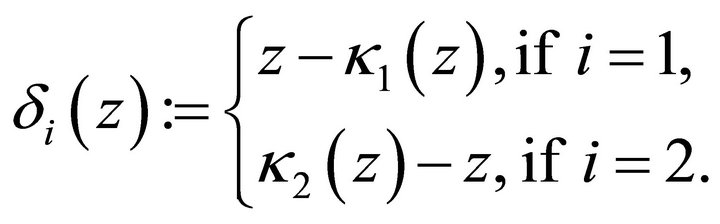
Lemma 5.1. For any  and the equilibria
and the equilibria  the following equations hold 1)
the following equations hold 1) 
2)  and 3)
and 3) .
.
Proof. The first claim follows directly from the definition of . Using Formula (7) we see that
. Using Formula (7) we see that
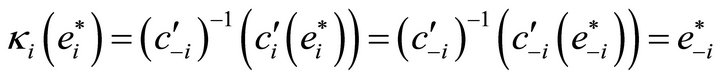
holds. And the last assertion follows from
 .
.
Lemma 5.2. For any  and
and 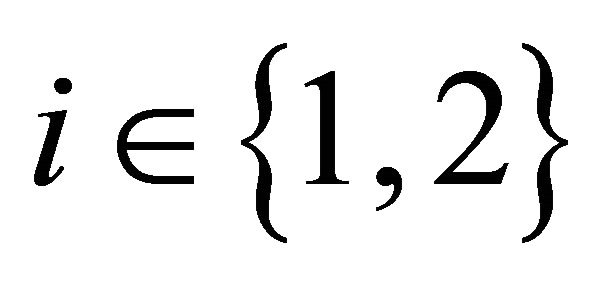 the expression
the expression  is non-negative.
is non-negative.
Proof. We only prove the lemma for![]() , the other case follows by an analogous argument. It suffices to show that
, the other case follows by an analogous argument. It suffices to show that 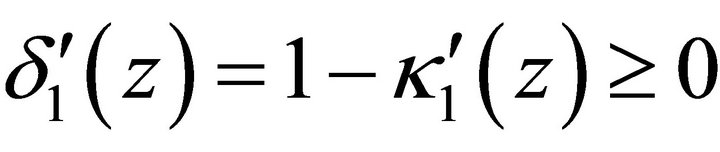 holds, because
holds, because .
.
By differentiating 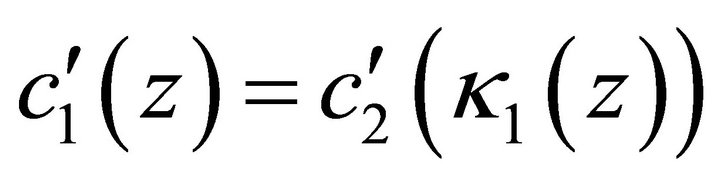 with respect to
with respect to , we obtain
, we obtain 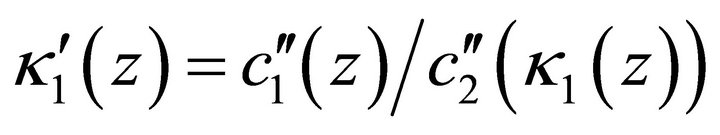 and it remains to prove
and it remains to prove . This, however, follows from
. This, however, follows from
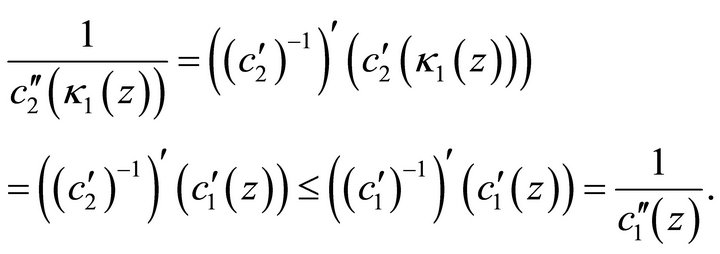
Lemma 5.3.
1) The derivative of  with respect to
with respect to ![]() is given by
is given by
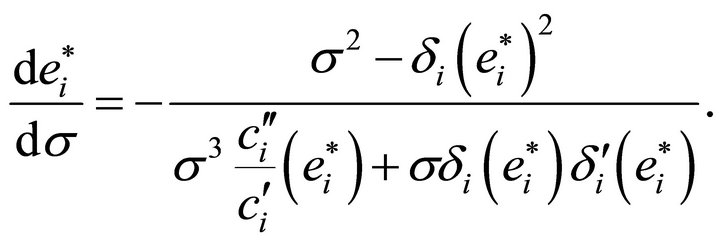
2) The equation  has a unique solution
has a unique solution . With
. With  denoting the corresponding effort level the evaluation of the second derivative of
denoting the corresponding effort level the evaluation of the second derivative of  at
at  is given by
is given by

Proof.
1) Applying the natural logarithm to Formula (6) and differentiating with respect to ![]() we get
we get
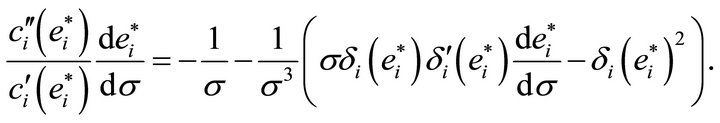
Redistributing the terms gives our claim.
2) The quotient rule yields the second derivative. For any solution  of
of  the following equations hold
the following equations hold

By Lemma 5.2, it then follows that the second derivative is negative in all extremal points, i.e. there are only maxima. This yields uniqueness.
Proof of Theorem 2.3. From Lemma 5.3, it follows directly that the derivative of 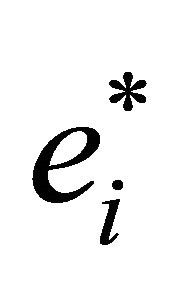 with respect to
with respect to ![]() vanishes independently of
vanishes independently of  if and only if
if and only if  holds. Moreover this is a maximum because by the same lemma the second derivative is negative. Substituting this result into Formula (6) we obtain
holds. Moreover this is a maximum because by the same lemma the second derivative is negative. Substituting this result into Formula (6) we obtain
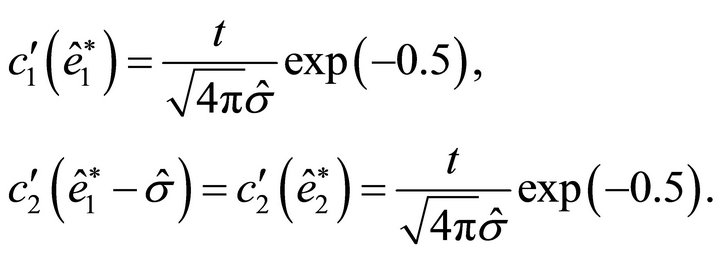
Taking the respective inverse functions and subtracting the two equations shows that
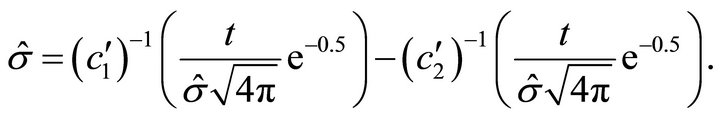
NOTES
1Similarly, [6] theoretically and experimentally studies active risk-taking in a field of heterogeneous contestants, but they regard risk-taking as the only choice variable (no effort choice). [7] again, analyzes both, risk-taking and effort choice, but in a symmetric tournament with homogeneous contestants.
2The existence of a pure-strategy equilibrium in a tournament model is not automatically assured (see e.g. the discussion in [1:845] or in [4: 106]). Rather, it needs a minimum amount of idiosyncratic risk in the tournament. Otherwise contestants would deduce their opponents’ effort levels from the publicly known cost functions and choose slightly higher effort levels than their opponents. As a result, there will only be mixed-strategy equilibria. In what follows, we assume that the idiosyncratic risk in the tournament is high enough to ensure the existence of a pure-strategy equilibrium.
3[4] takes a different road and model differing ability levels by introducing additive shift factors of different size into the production functions of the two contestants. [10] introduces contestant heterogeneity by modeling individual output as being the product of effort and ability level.
4Of course, we need to make sure that idiosyncratic risk is above the minimum level guaranteeing the existence of a pure-strategy equilibrium (see above). To argue our point the minimum level of risk required to obtain an equilibrium in pure strategies needs to be below the level of risk granting the highest effort level (see Figure 2). Even if this might not hold for a situation of very low contestant heterogeneity, this will clearly be the case for higher degrees of contestant heterogeneity (see Figure 3(b) vs. Figure 3(a)).
5The parameters for 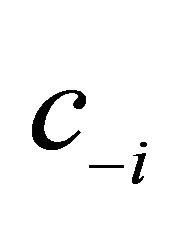 were chosen as follows: (a)
were chosen as follows: (a)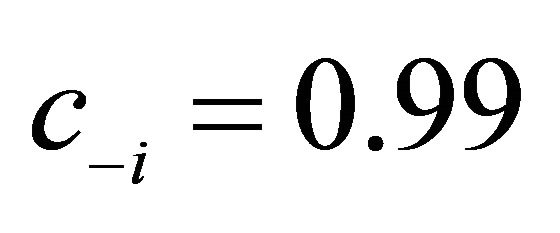 , (b)
, (b) . Again,
. Again,  and
and![]() .
.

