Theoretical Economics Letters
Vol.3 No.2(2013), Article ID:30800,9 pages DOI:10.4236/tel.2013.32016
Growth Theory and Endogenous Human Capital Development: A Contribution to the Theory of Complex Systems
Faculty of Economics, Business Administration and Social Sciences, University of Dortmund, Dortmund, Germany
Email: andreas.liening@uni-dortmund.de
Copyright © 2013 Andreas Liening. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 22, 2013; revised March 22, 2013; accepted April 12, 2013
Keywords: Bifurcation; Chaos Theory; Complexity Sciences; Endogenous Growth Theory; Human Capital
ABSTRACT
As economic phenomena become increasingly complex, the demands on models to reflect this complexity also increase. Economic growth, for example, which depends on a variety of factors, is such a complex phenomenon. Especially the relevance of human capital development for modern service societies is a significant growth factor. This is, however, considered only in few discussions. In order to represent such complex phenomena, adequate models are needed that go beyond linear approaches. This paper points out that models from the dynamic system theories are well suited to illustrate human capital as a factor of economic growth.
1. Introduction
The theory of complex systems can be considered a comparatively young scientific explanatory approach. To an increasing degree, this approach has also been incorporated into economics as a means to better understand order patterns created by free market systems.
von Hayek does not consider order as the result of planning. Rather, he postulates a constructivist error [1] and posits that order is paradoxical and due to an absolute misjudgment of these relations, as we frequently and consciously plan in the modern society because it has become so complex. Furthermore, he argues that we can only achieve an order of such complexity if we do not manage it according to a plan, which is, with the help of instructions, but aim to form a spontaneous order based on general rules instead.
Following von Hayek, such an order cannot be analyzed adequately with the help of frequently applied mechanistic models that are based on lineal1 cause-andeffect chains, which are predictable for this reason.
The development of the economic system as a whole or in particular domains, such as the business sector, is not characterized by fluent transitions. In fact, discontinuities, jump discontinuities and turbulences occur. Thus, economy and economy related subareas can be understood as non-linear, dynamic systems. It is in this context that complex systems are discussed.
To model complex developments that occur in reality, exogenic dysfunctions or random variables are traditionally used. Eventually, abnormal and non-continuous developments are analyzed with the help of methods that only appear applicable for lineal conditions or continuous processes. For a long time, economics was subordinate to the influence of a mechanistic world view, which applied, for example, to models whose trajectories, when tending toward the equilibrium, seemed to be predictable and tangible with the help of partial analyses.
However, in a society that increases in complexity, many economic explanatory approaches based on this world view are not particularly persuasive. Therefore, it is of particular importance to conduct research into new methods in the field of complex dynamic systems.
In many cases, the economic reality is much more difficult and complex than suggested by linear models2. For instance, it is not possible to explain self-organizing processes far from equilibrium with the help of linear views3.
The engagement of nonlinear, complex systems might play a decisive role in searching for an expansion of the economic toolbox, making it possible to represent a wide range of economic behavioral patterns and explanatory approaches. Using this approach, complexity can be described, analyzed and understood, whereas when applying traditional statistical methods, attempts to understand and analyze complexity fail entirely.
Non-linearity, feedback, irreversibility, self-organization and complexity are keywords in this approach whose subcategories can be subsumed under the key phrase “theory of complex systems”. In addition to the theory of self-organization, which is also called synergetics, one must mention Chaos Theory, a theory primarily concerned with questions of origination and analysis of complex order patterns.
Within the scope of its popular scientific upswing in the 1990s, Chaos Theory became the theory of a new homogeneous world explanation or world transfiguration4. Thus, advocates of Chaos Theory attempted to find chaos in the structures of remote galaxies or ascending wads of smoke of a cigarette, whereas opponents of the theory argued that chaos exists only in computer simulations and that there is no real-life application of the theory.
It is true that the possibility of researching chaos with connected order patterns in complex systems has not been imaginable until the development of modern computer technology. The multitude of calculations and the different types of visualization of complex structures were previously unrealizable. Consequently, it should not be astonishing that this theory gained momentum, particularly in the early 1990s.
However, the euphoria that accompanied the Chaos Theory subsided, and the number of popular scientific new publications decreased.
Simultaneously, the number of scientific publications that attempted to transfer important aspects of Chaos Theory to other areas of science increased. Economics has not been excluded, as one expects a better approach to economic reality from Chaos Theory than the neoclassical paradigm can render5.
As Chaos Theory is concerned with open dissipative dynamic systems, growth theory, an important sector of economics, assumes a degree of importance in this context. In the framework of growth theory, dynamization, feedback processes and non-linearity play decisive roles with respect to complexity.
Therefore, in the current article, (endogenous) growth theory shall be considered exemplary6. Throughout the 1970s, it was argued that the “limits of growth” [18] and zero growth were demanded by certain parts of society, but today, there is a considerable awareness that without economic growth, neither advancement nor maintenance of the status quo is possible7. Thus, the relevance of human capital for modern service societies is increasingly recognized without the existence of adequate illustrations in the numerous considerations on growth theory.
This paper contributes to the literature by presenting the dynamic progression of economic growth in terms of the theory of complex systems and introducing the possibility of integrating the importance of human capital into this dynamic progression.
2. The Old Growth Theory
In contrast to post-Keynesian models, the neoclassical Solow model can be referred to as a culmination of the old growth theory. In this neoclassical model, it is implied that there is only one production sector, one good, no foreign countries and no governmental activities. Accordingly, it is like the other growth models, as it has very restrictive assumptions8.
The production function takes precedent in the neoclassical growth theory and is the central neoclassical instrument for theoretical analysis. The production function describes the connection between input and output such that the input consists of two factors of production: labor 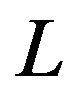 and capital
and capital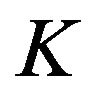 . Accordingly, the production function can generally be specified in the following manner:
. Accordingly, the production function can generally be specified in the following manner: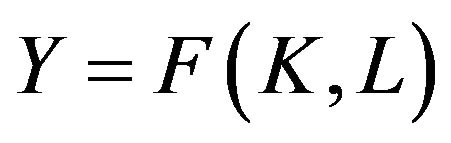 , where
, where 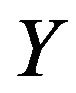 symbolizes the output [14].
symbolizes the output [14].
If one considers the production function as a simplification, not twobut one-dimensionally, by considering the output per worker, the following equation, under certain conditions (constant returns to scale), is derived from
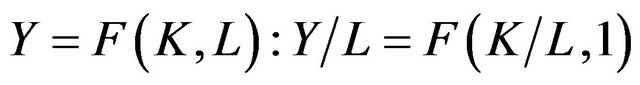 or
or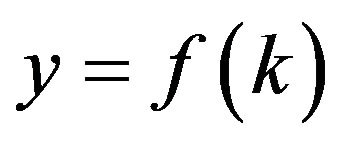 .
.
Here, the output per worker is symbolized by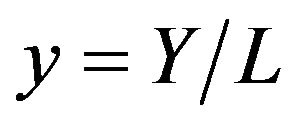 , and the capital per worker is symbolized by
, and the capital per worker is symbolized by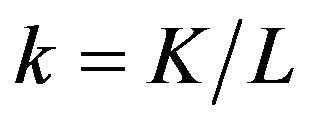 . Expanded by the possibility of technical advancement, one obtains
. Expanded by the possibility of technical advancement, one obtains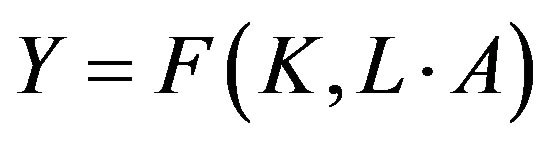 , where
, where  is the work efficiency. Then,
is the work efficiency. Then, 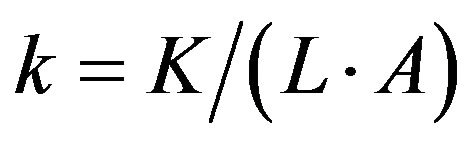 is the capital intensity for
is the capital intensity for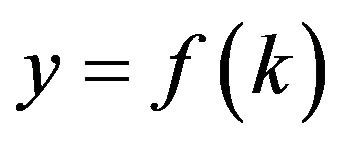 . We define capital intensity as the capital per capita and work efficiency.
. We define capital intensity as the capital per capita and work efficiency.
An essential result of this theory can be seen in the case of a given saving ratio and identity of economic saving and investment where the long term growth rate of an economy is determined by the growth rate of the population as well as the growth rate of average labor productivity and technical advancement.
The parameters that influence long-term growth (such as population growth and technical advancement) are given exogenously in this model. This also applies for the rate of investment, which in this case—and this is criticized frequently—has no enduring effect on the longterm growth. However, it must be emphasizes that all relevant parameters that guarantee enduring growth are considered exogenously in this context, thus acting as external inferences.
3. The New Growth Theory
3.1. Transition to the New Theory
The relatively unsatisfactory approach, which interprets long-term growth as an exogenous shock, can be modified in such a way that a more realistic model emerges, whose growth determinants are based on the concept of growth as a self-organizing process. The objective must be to specify a model that does not solely denote growth processes by fluent transitions, but a model that allows discontinuities, eruptive changes and turbulences. Only by this means can an economy be regarded as a non-linear, dynamic or complex system. The new growth theory results from these and numerous other considerations.
3.2. Relevance of the Formation of Human Capital and the Entrepreneurial Spirit
In an economy such as Germany, in which almost no natural resources exist, high-quality research and development results play an important role. To obtain such results, highly trained employees are required. Therefore, human capital is an essential and central factor of modern economies9. Human capital will be considered as a production factor, which comprises the abilities, skills and knowledge being internalized by humans during their life span.
On the basis of Romer’s view, the neoclassical production function is to be expanded by a factor that includes this aspect. This, then, results in the fact that human capital in the growth model is endogenized. In this endogenization lies the new quality of growth theory, which can also be referred to as endogenous growth theory.
Thus, the assumption of an exogenously given technical advancement is neutralized. Whereas the neoclassical growth theory assumes that technical and scientific achievements are given factors, the new growth theory asserts to endogenize every important factor.
Accordingly,
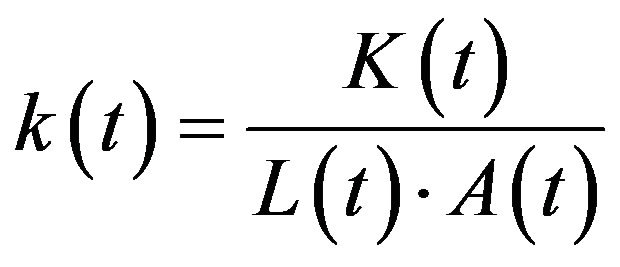 (1)
(1)
and
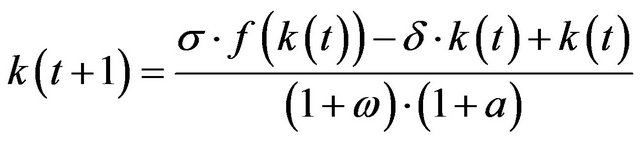 10, (2)
10, (2)
where 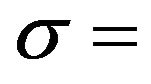 saving rate,
saving rate, 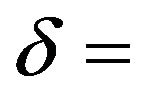 depreciation rate,
depreciation rate, 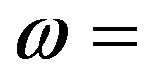 population growth rate,
population growth rate, 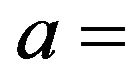 technological advancement, and
technological advancement, and
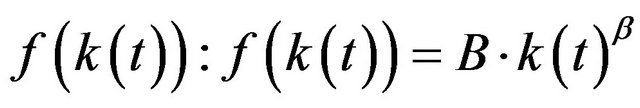 .
.
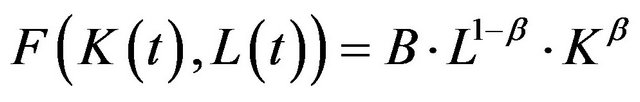 is the Cobb-Douglas production function, with
is the Cobb-Douglas production function, with 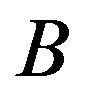 as a level parameter and
as a level parameter and  as a parameter of substitution.
as a parameter of substitution. 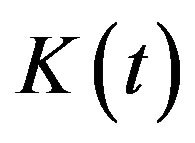 is the capital (monetary capital and capital equipment) dependent on time t, capital is considered capital per capita or takes the work efficiency per efficiency unit into account such that
is the capital (monetary capital and capital equipment) dependent on time t, capital is considered capital per capita or takes the work efficiency per efficiency unit into account such that
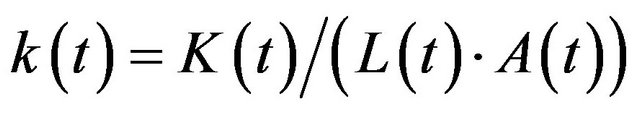 . Here,
. Here, 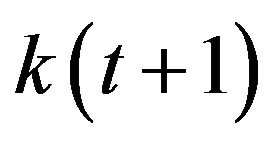 is dependent on investments
is dependent on investments 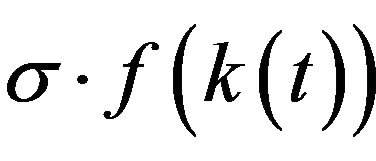 minus depreciations
minus depreciations 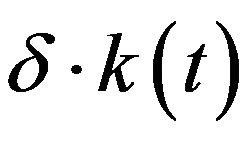
plus capital intensity of the past period. In turn, this term is dependent on the exogenously given population growth  and the exogenously given technological advancement
and the exogenously given technological advancement . Parameter
. Parameter  represents the factor by which the work efficiency changes, which, among other things, depends on the standard of knowledge of the labor force.
represents the factor by which the work efficiency changes, which, among other things, depends on the standard of knowledge of the labor force.
Based on a technological level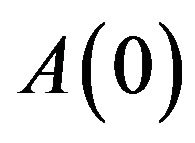 , technological advancement increases by the factor
, technological advancement increases by the factor , that is,
, that is,
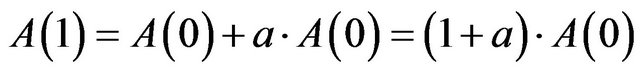 .
.
For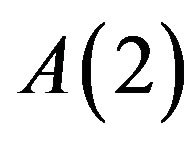 , analogously,
, analogously,
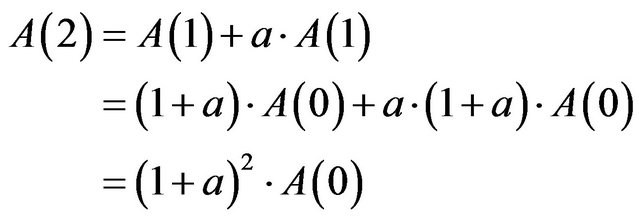 .
.
Thus, the following result for technological advancement after 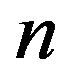 periods is
periods is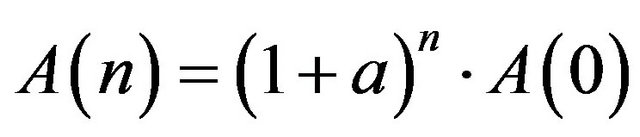 . That is, in every period, the technological advancement changes by the factor
. That is, in every period, the technological advancement changes by the factor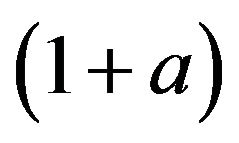 . If one acts on the assumption of capital intensity, that is, the quotient of capital and work,
. If one acts on the assumption of capital intensity, that is, the quotient of capital and work,
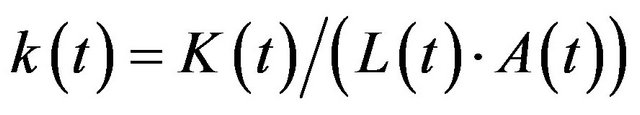 , for a certain period
, for a certain period , then one apparently obtains the following result for
, then one apparently obtains the following result for  such that
such that 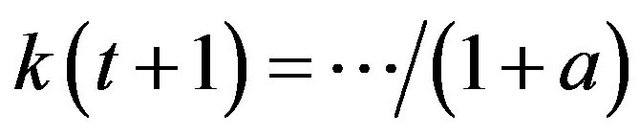 as considered above.
as considered above.
The population growth rate  has demonstrated similar effects on the capital intensity as technological advancement.
has demonstrated similar effects on the capital intensity as technological advancement.
Lucas [21] emphasizes two effects that result from the integration of the development of human capital into an economic growth model. The first effect describes how the human capital levels affect current production, while the second effect considers the way how the accumulation of human capital is affected by the current time allocation.
To integrate these two effects into the model, one therefore assumes that the rate of change of knowledge and competencies is dynamic and depends on the capital accumulation.
The function of human capital is given by
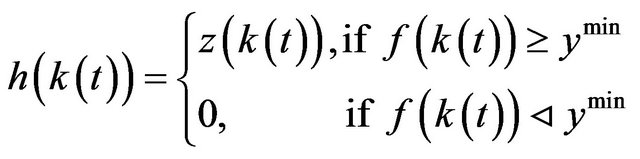 , (3)
, (3)
with
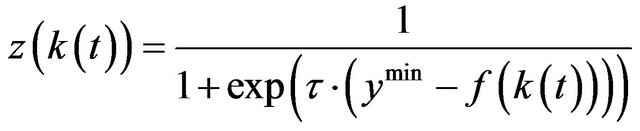 . (4)
. (4)
Here, it is assumed that the change of human capital  is always positive from a certain income per worker onward and that, over the course of time; it increases according to the law of diminishing returns with the monetary capital and the capital equipment or, more precisely, per efficiency unit (Figure 1).
is always positive from a certain income per worker onward and that, over the course of time; it increases according to the law of diminishing returns with the monetary capital and the capital equipment or, more precisely, per efficiency unit (Figure 1).
In this example, 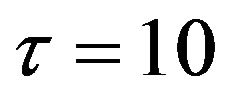 ,
,  , and in the production function,
, and in the production function, 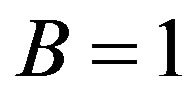 and
and 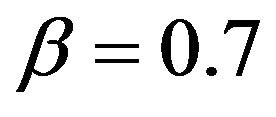 are fixed values.
are fixed values.
It is plausible to assume that the human capital will stagnate in the medium term when one falls below the assumed minimum of income per worker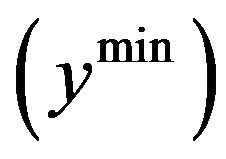 . The assumption that in the case of a low income, knowledge stagnates instead of decreases is consistent with the pre-
. The assumption that in the case of a low income, knowledge stagnates instead of decreases is consistent with the pre-
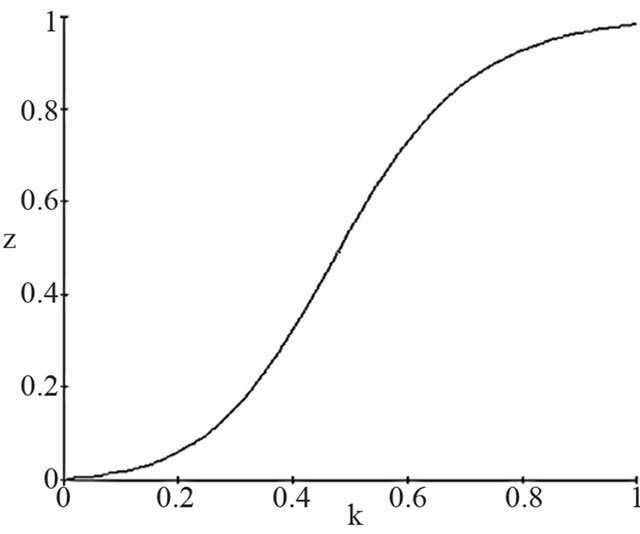
Figure 1. Endogenous growth of human capital according to the law of diminishing returns.
conception held by Romer11.
Overall, on one hand, the possibility of an increased per capita income can grow with increased human capital, increased standards of knowledge and increased levels of competence. On the other hand, an increased per capita income can effectuate the possibility of an increased standard of knowledge and level of competence. Therefore, the individual utility can be interpreted from both directions—education or income.
However, it is not simple to apply this individual situation to the economy as a whole. Let us assume that neither innovations nor technological changes have occurred in the last 100 years. The population would still use carriages to drive through the country and sail ships to cross the oceans. One could enhance the creation of human capital by allowing greater parts of society access to higher education, or one could accelerate the (physical) capital accumulation by producing more sailing ships and carriages. At some point, however, it would be necessary to realize that the economic utility would be only marginal if one additional high school graduate drove one additional carriage [22].
In other words, if one considers the situation from an economic point of view, it becomes obvious that increased human capital does not inherently result in increased economic income advancement. Rather, it is the innovation, creativity, inventive talent and entrepreneurship, as confirmed by Schumpeter [23], which increases human capital and results in a higher standard of living, which is expressed in per capita income12.
Therefore, it is implicitly assumed in the model that between human capital and monetary capital/capital equipment per capita, existing a transmission effect, which can be characterized by terms such as innovation and entrepreneurship.
Ultimately, we derive the following formula for capital intensity:
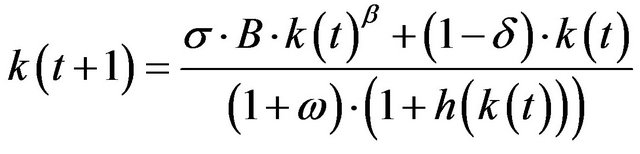 , (5)
, (5)
where  represents the human capital function.
represents the human capital function.
In the context of the correspondent formation of competence for the development and support of such an effect, it is referred to as entrepreneurship education13. Apart from a competence orientation, the importance of a basis of values should be considered when entrepreneurs or intrapreneurs are educated or further their education. Education in the form of entrepreneurship education furthers economic creativity, responsibility, decision-making ability and independence, as well as the ability to take responsibility for others. In doing so, one should focus on self-organized learning that is inspiring and combined with construction. With the help of methods that activate the learners, this will bring forth judgment competence, decision-making competence, skills and abilities [28]. This could possibly positively intensify the transmission effect. A first illustration of the new growth model is shown in Figure 2.
Here, the saving rate amounts to 40%, i.e.,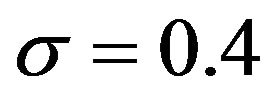 . For simplification of the analysis, the population growth rate is 0%, i.e.,
. For simplification of the analysis, the population growth rate is 0%, i.e., . The depreciation rate is
. The depreciation rate is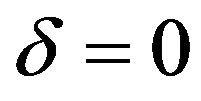 . In the human capital function
. In the human capital function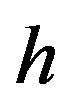 , we have
, we have 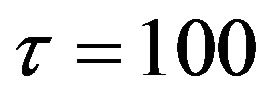 and
and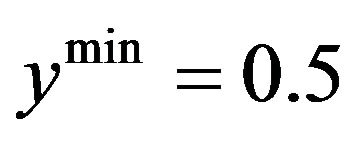 . In the production function, the level parameter is
. In the production function, the level parameter is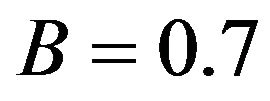 , and the substitution parameter is assumed to be
, and the substitution parameter is assumed to be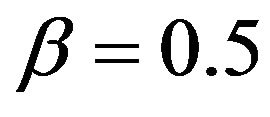 . The reason for this can be found in the previous remarks on the neoclassical model. In addition, it should be annotated that a change of the saving rate can explain a short-term change of the economic growth at the most, but in no case can endure growth be explained. In the original neoclassical model, particularly the exogenously defined population growth and the exogenously given technological advancement could explain enduring growth. In contrast to the neoclassical Solow model, in this model, technological advancement is implicitly explained by the endogenous function for the formation of human capital.
. The reason for this can be found in the previous remarks on the neoclassical model. In addition, it should be annotated that a change of the saving rate can explain a short-term change of the economic growth at the most, but in no case can endure growth be explained. In the original neoclassical model, particularly the exogenously defined population growth and the exogenously given technological advancement could explain enduring growth. In contrast to the neoclassical Solow model, in this model, technological advancement is implicitly explained by the endogenous function for the formation of human capital.
The parameters are chosen accordingly such that ceteris paribus of the endogenously defined formation of human capital, with its transmission effect, comes into
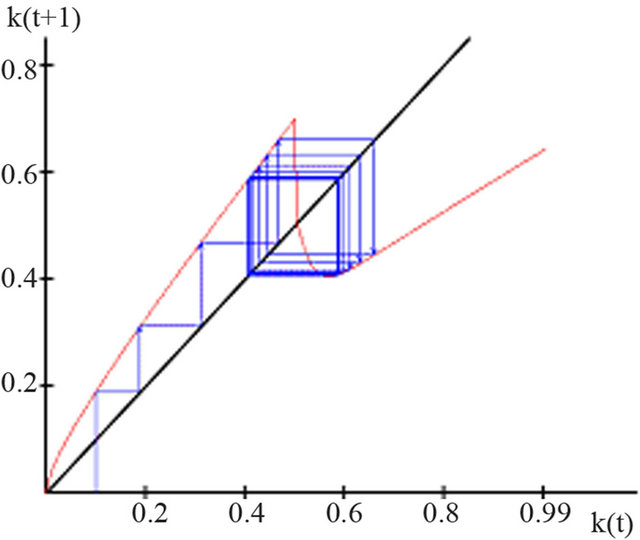
Figure 2. Double cycle attractor for the capital intensity function k(t + 1) in the growth model with endogenous formation of human capital.
question as a cause for enduring growth.
For very low values  of capital intensity, that is, money capital and capital equipment per capita or per efficiency unit, the development of human capital stagnates, resulting in the uninterrupted growth of money and capital equipment efficiency, which is measured in efficiency units. For that, it must be presumed that the per capita capital can be found, as in the initial situation, below the steady state in the growth equilibrium14. If the critical point
of capital intensity, that is, money capital and capital equipment per capita or per efficiency unit, the development of human capital stagnates, resulting in the uninterrupted growth of money and capital equipment efficiency, which is measured in efficiency units. For that, it must be presumed that the per capita capital can be found, as in the initial situation, below the steady state in the growth equilibrium14. If the critical point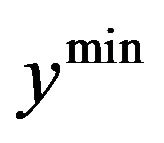 , the minimum income necessary for an increase in knowledge and level of competence, is reached, the human capital begins to grow according to the law of diminishing returns as the work efficiency increases via the transmission effect. Initially, this results in a decline of the capital and capital equipment efficiency.
, the minimum income necessary for an increase in knowledge and level of competence, is reached, the human capital begins to grow according to the law of diminishing returns as the work efficiency increases via the transmission effect. Initially, this results in a decline of the capital and capital equipment efficiency.
With the given parameter constellation, it becomes apparent that at a certain basic value of capital intensity  a balance is reached, which displays a double cycle. This results from the fact that the critical value
a balance is reached, which displays a double cycle. This results from the fact that the critical value 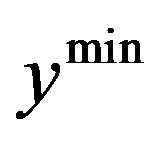 is undershot repeatedly at the current parameter constellation, which stagnate the standard of knowledge and level of competence. This leads to a short-term increase in capital and capital equipment intensity, as henceforth, the work efficiency is lower than before. This short-term increase, however, causes the critical value to be exceeded and human capital to grow. Finally, an increase in work efficiency occurs together with a short-term decrease of capital and capital equipment intensity.
is undershot repeatedly at the current parameter constellation, which stagnate the standard of knowledge and level of competence. This leads to a short-term increase in capital and capital equipment intensity, as henceforth, the work efficiency is lower than before. This short-term increase, however, causes the critical value to be exceeded and human capital to grow. Finally, an increase in work efficiency occurs together with a short-term decrease of capital and capital equipment intensity.
This clarifies that the growth effect caused by the endogenous explanation of the accumulation of human capital can by no means result in a constant increase of the gross national product. Rather, fluctuations arise, which, as in the aforementioned parameter constellation, can lead to constant oscillations. The next illustration (Figure 3) demonstrates this process with regard to the development of capital intensity in chronological sequence.
At this point, it should be noted that the endogenization of the standard of knowledge and the level of competence can also have, in addition to a regular progression as described previously, an irregular money capital and capital equipment-per-capita development as a result.
In the following bifurcation diagram the capital intensity, 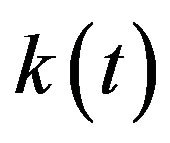 , is presented in relation to the substitution parameter
, is presented in relation to the substitution parameter  of the production function (Figure 4).
of the production function (Figure 4).
This parameter indicates how strongly the production factor labor is when substituted by the production factor capital (money capital and capital equipment) in the production function. It thus becomes obvious that in the case of increasing values of the substitution parameter of the production function, the development of capital intensity is not stable but instead is interrupted repeatedly by phases of irregular development15.
The bifurcation diagram shows that at approximately 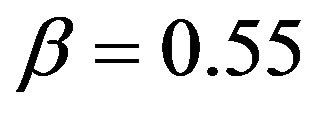 and
and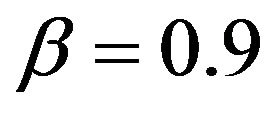 , attractor areas are situated, which are likely described as chaotic due to their struc-
, attractor areas are situated, which are likely described as chaotic due to their struc-
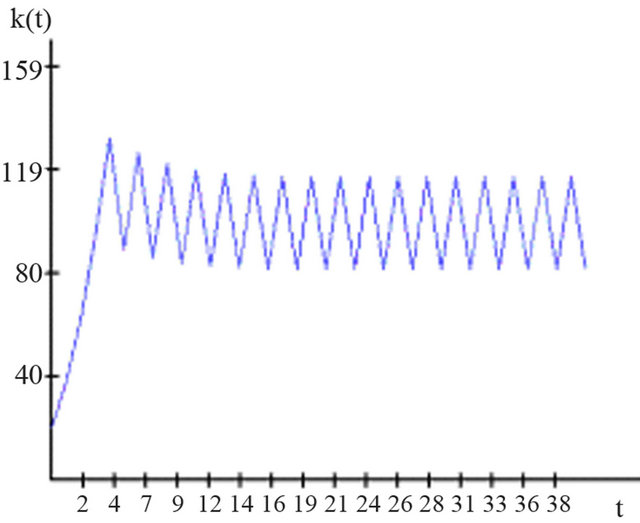
Figure 3. Cyclic development of capital intensity in the growth model with endogenous formation of human capital.
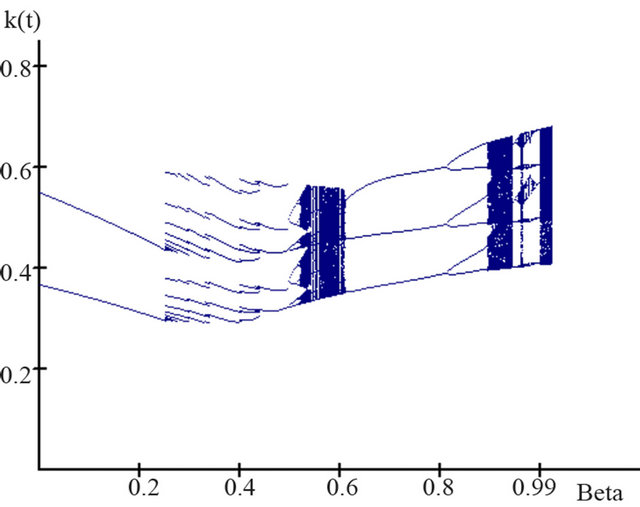
Figure 4. Bifurcation diagram for the growth model with endogenous formation of human capital.
ture. Figure 5 shows one of these strange attractors at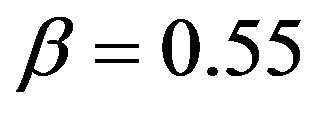 , and the development of capital per efficiency unit is presented.
, and the development of capital per efficiency unit is presented.
The typical characteristic of strange attractors is the range in which the capital intensity moves. However, the precise position is not definable.
Figure 6 shows the just elucidated situation over a specific period.
Irregular fluctuations that do not suggest a regular pattern are plainly visible.
A more precise analysis, by means of a calculation of Lyapunov exponents16 for several  -values, supports the assumption that chaos develops over a specific period. The Lyapunov exponent indicates how the trajectories of two proximate initial values develop in relation to each other. If the Lyapunov exponent is positive, both trajectories exponentially and strongly drift apart. In other words, the butterfly effect completely develops; that is, minimal changes in the initial conditions lead to enormous differences in the results.
-values, supports the assumption that chaos develops over a specific period. The Lyapunov exponent indicates how the trajectories of two proximate initial values develop in relation to each other. If the Lyapunov exponent is positive, both trajectories exponentially and strongly drift apart. In other words, the butterfly effect completely develops; that is, minimal changes in the initial conditions lead to enormous differences in the results.
Figure 7 presents a diagram showing the money capital and capital equipment per capita development in the
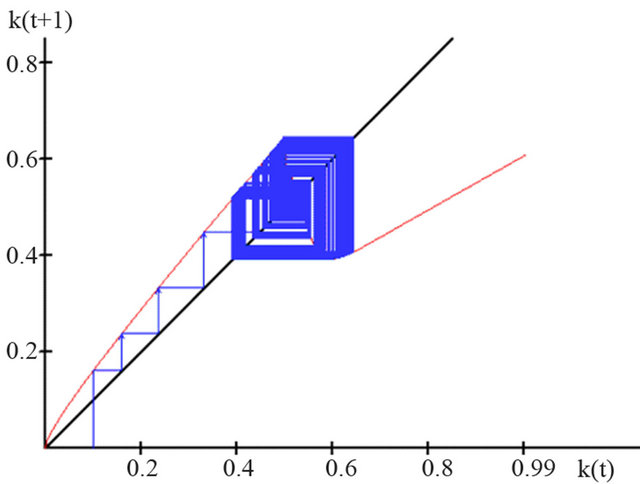
Figure 5. Strange attractor in the development of capital intensity in the growth model with β = 0.55.
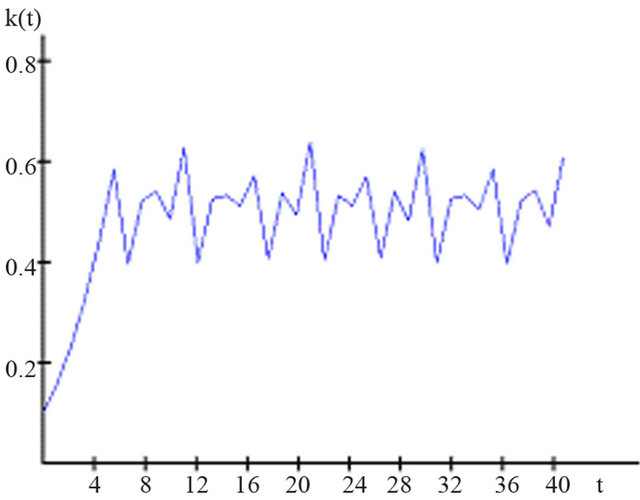
Figure 6. Chaotic development of the capital intensity in the growth model with β = 0.55.
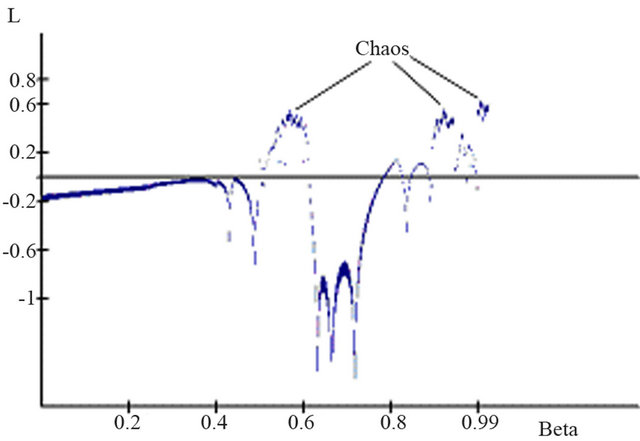
Figure 7. Lyapunov diagram for growth model with endogenous formation of human capital.
Lyapunov exponents for different  -values17. Comparing the Lyapunov diagram with the bifurcation diagram, it is apparent that the zones, which were assumed to be chaotic in the bifurcation diagram, are in fact chaotic.
-values17. Comparing the Lyapunov diagram with the bifurcation diagram, it is apparent that the zones, which were assumed to be chaotic in the bifurcation diagram, are in fact chaotic.
Finally, we can see (Figure 8) the growth progress for the total output of an economy, which was generated with the help of the developed model. An essential motor of the growth is the influence of the development of endogenous human capital. This facilitates, by means of the transmission effect circumscribed with expressions such as innovation and entrepreneurial spirit, a positive, even exponential growth trend that is pervaded by irregular phases.
Finally, we can see (Figure 8) the growth progress for the total output of an economy, which was generated with the help of the developed model. An essential motor of the growth is the influence of the development of endogenous human capital. This facilitates, by means of the transmission effect circumscribed with expressions such as innovation and entrepreneurial spirit, a positive, even exponential growth trend that is pervaded by irregular phases.
3.3. Summary of the Analysis
The preceding analysis showed that the endogenization of human capital in the growth model can lead to a nonlinear, dynamic or complex system that is able to organize itself and allows discontinuities, eruptive changes and turbulences in the growth process. This allows a dynamic change of knowledge and competencies and therefore gives an implicit explanation of technological advancement.
Depending on the parameter constellation, the development of the capital intensity, which depends on the endogenous accumulation of human capital, can display a double cycle, resulting from the fact that the critical value 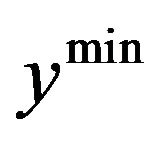 is undershot repeatedly and leading to con-
is undershot repeatedly and leading to con-
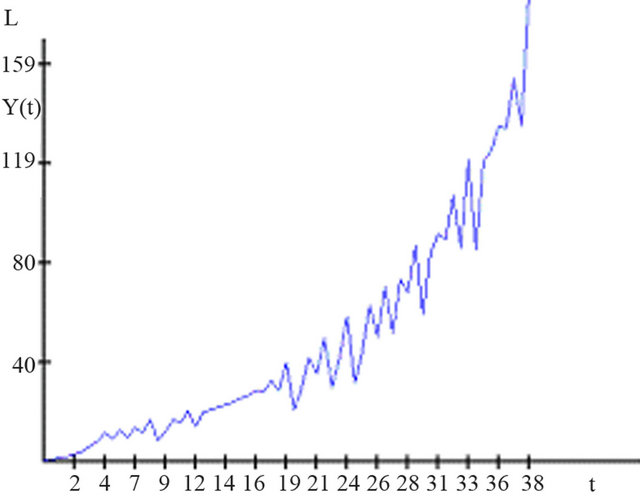
Figure 8. Irregular growth cycles—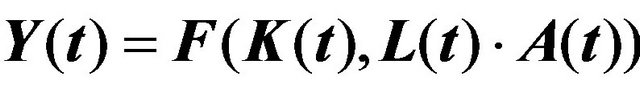 .
.
stant oscillations. However, a change in the substitution parameter  can lead to an unstable and chaotic development of capital intensity, resulting in a strange attractor. The calculation of Lyapunov exponents for several
can lead to an unstable and chaotic development of capital intensity, resulting in a strange attractor. The calculation of Lyapunov exponents for several  -values endorsed the existence of a butterfly effect for specific intervals of
-values endorsed the existence of a butterfly effect for specific intervals of .
.
4. Concluding Remarks
Overall, it can be recapitulated that in the model being developed, a growth effect through the accumulation of human capital can arise. However, it is marked by partly irregular changes, opposed to constant fluctuations, in the national product. To achieve a positive effect of human capital on economic growth within the scope of this model, a transmission effect is required, which here was circumscribed with expressions such as entrepreneurial spirit. Therefore, an increase in human capital alone does not by itself accelerate economic growth in this model.
Because of this exemplary consideration, the facilitation of the entrepreneurial spirit, in terms of entrepreneurship education, is therefore essential for a working transmission effect.
Apart from that, the analysis of the model demonstrates that the new concept does not inevitably lead to a complete break from the neoclassical view. Rather, there are starting points from which neoclassical elements can be integrated into the new view as a special case by means of modification.
Therefore, the new theory is by no means substitutive; rather, it is complementary to the neoclassical view. Thus, it is possible, as in the presented example, to establish a connection between the neoclassical and new growth theories.
One certainly cannot expect that a relatively basic model such as the one being developed here to accurately mirror reality. Such expectations cannot be fulfilled by these types of models if one follows the logic of complex systems. However, with the help of these models, basic characteristics of non-linear economic systems can be illustrated. Furthermore, a closer analysis reveals that such models allow a wide range of possibilities and explanatory models that go far beyond the informational value of traditional models. This is a sign that the consideration of complex systems in economics is not only functional but also necessary if one wants to avoid Laplace’s demon of a linear-causal economic world. Considered altogether, it is also possible to assign Solow’s statement on the enlightening character of his models with peace of conscience to the developed non-linear model:
“I don’t think that models like this lead directly to prescription for policy or even to detailed diagnosis. But neither are they a game. They are more like reconnaissance exercises.” [30]
REFERENCES
- F. A. von Hayek, “Die Anmaßung von Wissen,” MohrSiebeck, Tübingen, 1996.
- A. Liening, “Econoplexity: The Breakdown of the Traditional Mechanistic Worldview, the Development of Complexity Sciences and the Pretence of Knowledge in Economics,” Modern Economy, Vol. 4, No. 4, 2013, pp. 305- 319.
- P. Nijkamp and J. Poot, “Lessons from Nonlinear Dynamic Economics,” Springer, New York, Berlin, Heidelberg, New York, 1993.
- R.-A. Dana and L. Montrucchio, “Dynamic Complexity in Duopoly Games,” Journal of Economic Theory, Vol. 40, No. 1, 1986, pp. 40-56. doi:10.1016/0022-0531(86)90006-2
- F. Bestenreiner, “Der Phantastische Spiegel,” Moos u. Partner, München, 1989.
- B. B. Mandelbrot and R. L. Hudson, “Misbehavior of Markets,” Basic Books, New York, 2004.
- F. Trosky, “Heterogene Erwartungen auf dem Geldmarkt,” Duncker & Humblot, Berlin, 2005.
- T. Büssow, “Chaostheorie und Unternehmenssteuerung: Konstruktionen zur Modellgestützten Entscheidungsvorbereitung,” Deutscher Universitäts-Verlag, Wiesbaden, 2003.
- G. Zehetner, “Anwendungen der Chaostheorie in der Betriebswirtschaftslehre,” Facultas, Wien, 2003.
- T. Puu, “Attractors, Bifurcations & Chaos: Nonlinear Phenomena in Economics,” Springer, New York, 2003. doi:10.1007/978-3-540-24699-2
- G. Antinolfi, T. Keister and K. Shell, “Growth Dynamics and Returns to Scale: Bifurcation Analysis,” Journal of Economic Theory, Vol. 96, No. 1-2, 2001, pp. 70-96. doi:10.1006/jeth.1999.2632
- T. Mitra and K. Nishimura, “Discounting and Long-Run Behavior: Global Bifurcation Analysis of a Family of Dynamical Systems,” Journal of Economic Theory, Vol. 96, No. 1-2, 2001, pp. 256-293. doi:10.1006/jeth.2000.2642
- L. Gardini, I. Sushko and A. K. Naimzada, “Growing through Chaotic Intervals,” Journal of Economic Theory, Vol. 143, No. 1, 2008, pp. 541-557. doi:10.1016/j.jet.2008.03.005
- R. M. Solow, “A Contribution to the Theory of Economic Growth,” The Quarterly Journal of Economics, Vol. 70, No. 1, 1956, pp. 65-94. doi:10.2307/1884513
- P. M. Romer, “Increasing Returns and Long-Run Growth,” Journal of Political Economy, Vol. 94, No. 5, 1986, pp. 1002-1037. doi:10.1086/261420
- R. Deneckere and S. Pelikan, “Competitive Chaos,” Journal of Economic Theory, Vol. 40, No. 1, 1986, pp. 13-25. doi:10.1016/0022-0531(86)90004-9
- M. Otaki, “A Keynesian Endogenous Growth Theory with a Rigorous Microeconomic Foundation,” Theoretical Economics Letters, Vol. 2, No. 4, 2012, pp. 365-368. doi:10.4236/tel.2012.24067
- D. H. Meadows, C. O. Rome and P. Associates, “The Limits to Growth: A Report for the Club of Rome’s Project on the Predicament of Mankind,” Universe Books, New York, 1972.
- H. Siebert, “Jenseits des Sozialen Marktes,” Deutsche Verlags-Anstalt, München, 2005.
- R. H. Day, “Irregular Growth Cycles,” American Economic Review, Vol. 72, No. 3, 1982, pp. 406-414.
- R. E. Lucas, “On the Mechanics of Economic Development,” Journal of Monetary Economics, Vol. 22, No. 1, 1988, pp. 3-42. doi:10.1016/0304-3932(88)90168-7
- A. Liening, “Ökonomische Chaostheorie,” H. May, Ed., Lexikon der Ökonomischen Bildung, Wien, 1996.
- J. Schumpeter, “Theorie der Wirtschaftlichen Entwicklung,” Duncker & Humblot, Berlin, 1934.
- B. Ziesemer, “Eine Kurze Geschichte der Ökonomischen Unvernunft: Die Deutsche Wirtschaftspolitik und das Gesetz der Unbeabsichtigten Folgen,” Campus, Frankfurt, New York, 2007.
- R. Cantillon, “Essai sur la Nature du Commerce en Gé- néral,” Institut National d’Ètudes Démographique, Paris, 1952.
- R. B. Emmett, “The Economist and the Entrepreneur: Modernist Impulses in Risk, Uncertainty, and Profit,” History of Political Economy, Vol. 31, No. 1, 1999, pp. 29-52.
- H. Mandl and J. Hense, “Lernen Unternehmerisch Denken: Das Projekt Tatfunk,” München, 2004.
- A. Liening, “Komplexe Systeme zwischen Ordnung und Chaos,” Lit, Münster, Hamburg, London, 1999.
- M. Schönhofer, “Chaotic Learning Equilibria,” Journal of Economic Theory, Vol. 89, No. 1, 1999, pp. 1-20. doi:10.1006/jeth.1999.2509
- R. M. Solow, “Growth Theory: An Exposition,” Oxford University Press, New York, Oxford, 1987.
Appendix
Calculation of the Lyapunov Exponents for the Growth Formula
It is commonly known that the Lyapunov exponent is calculated where
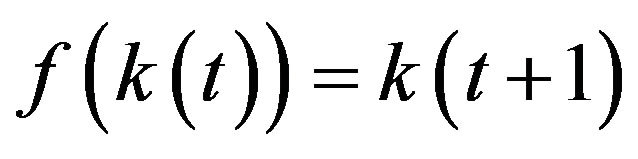 as follows:
as follows:
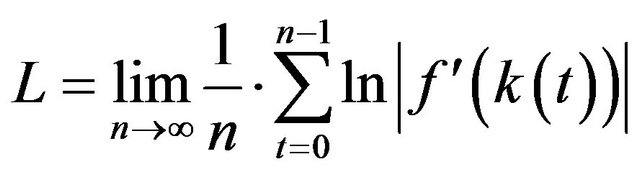 .
.
Regarding the definition of the Lyapunov exponent, cf., (e.g., Schönhofer [29] or Liening [28]).
Therefore, the first derivative of the growth formula
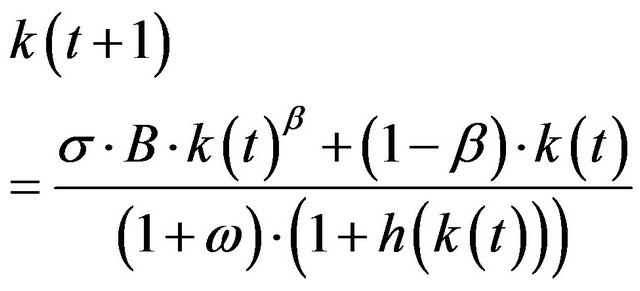
must be determined. The knowledge function h, as far as per capita income is concerned, leads to a stagnating development that otherwise agrees with the law of diminishing returns that can be substantiated by h = 0 or
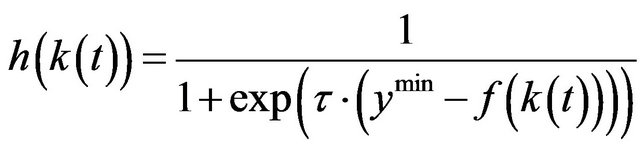 .
.
There are two derivations.
If 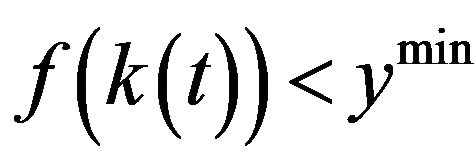 equals the first derivation of
equals the first derivation of , then
, then
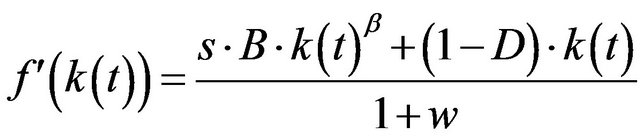
Given the case that 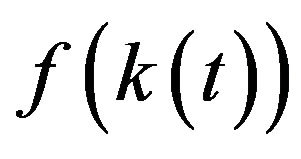 is greater than or equal
is greater than or equal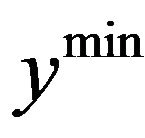 , after a simple transformation we obtain the following result (see the Equation at the end).
, after a simple transformation we obtain the following result (see the Equation at the end).
With the help of a computer program, the Lyapunov exponent can be determined. To do so, the basic equation is iterated approximately 500 times to make certain that 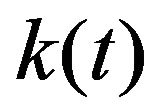 is located on the attractor (provided one exists). Afterward, the Lyapunov exponent can be determined whereby the calculation of the limiting value for n toward infinity has to be interrupted after a finite period. After approximately 2500 iterations, the calculated value is so precise that further iterations would only insignificantly alter the Lyapunov exponent. The figure (Figure 7) of the Lyapunov diagraph is the result of this calculation.
is located on the attractor (provided one exists). Afterward, the Lyapunov exponent can be determined whereby the calculation of the limiting value for n toward infinity has to be interrupted after a finite period. After approximately 2500 iterations, the calculated value is so precise that further iterations would only insignificantly alter the Lyapunov exponent. The figure (Figure 7) of the Lyapunov diagraph is the result of this calculation.
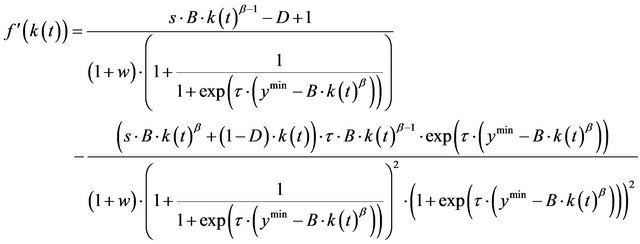
NOTES
1“Lineal systems are conceptions in which the elements of the system are arranged consecutively as a chain” [2].
2Therefore, Nijkamp and Poot, with good reason, assert: “Our economic world is highly dynamic and exhibits a wide variety of fluctuating patterns. This forms a sharp contrast with our current economic toolbox, which is largely filled with linear and comparative static instruments” [3].
3Conversely, it is not difficult to characterize a Markov-perfect equilibrium (MPE) using dynamic programming methods in the field of dynamic complexity [4]. This methodical approach can also include chaos MPE [4].
4With regard to popular scientific literature, one should refer to Bestenreiner [5].
5In the recent past, numerous interesting publications concerned with Chaos Theory and economics have been published. The following monographs are cited: Mandelbrot and Hudson [6], Trosky [7], Büssow [8], Zehetner [9], Puu [10].
6There are different articles that discuss growth theory using the ideas of the complexity sciences. An example is the article by Antinolfi et al., who investigated the dependence of the dynamic behavior of an endogenous growth model on the degree of returns of scale [11]. Another example is the paper by Mitra and Nishimura [12], who used bifurcation analysis to investigate discounting and long-run behavior. Within their growth model, Gardini et al. [13] used the mechanism of capital accumulation (cp. Solow) [14] and the process of technical change and innovation (cp. Romer) [15], to discuss chaotic intervals within the dynamics of this model. Deneckere and Pelika [16], for instance, indicated that the dynamics of optimal growth paths could be arbitrarily chaotic or complex. They doubt that in these cases, it is likely that there exist learning mechanisms for perfect foresight, which is normally assumed [16]. There have, of course, been more recent approaches beyond the complexity sciences, which favour an endogenous theory of economic growth as Otaki [17] does in his article.
7Cp. for this, refer to what was already annotated in the year 1974 by von Hayek [1].
8Thus, Solow offers this annotation: “All theory depends on assumptions which are not quite true. That is what makes it theory” [14].
9Production factors such as labor and capital, as well as technological advancement, result in economic growth. This concept applies to industrial and service societies, but not to knowledge-based societies, as emphasized by Siebert [19], in which human capital develops into an essential growth determinant.
10By modifying the neoclassical growth model of Solow [14], Richard Day [20] had already given in 1982 straightforward impulses regarding non-linear dynamization or the possibility of chaos in such models. To demonstrate the influence of the endogenization of human capital development, the mentioned growth-model of Day has been developed further. The initial situation is the illustrated neoclassical model, in which the capital-intensity per efficiency unit is considered. Day’s proposal can be considered a special case that results first by excluding the technological advancement, second by setting the depreciation 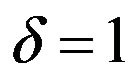 and third by adding a “cleanliness factor” to the per capita production function.
and third by adding a “cleanliness factor” to the per capita production function.
11Accordingly, Romer states, “Knowledge does not depreciate” [15].
12Solow, for example, assumes that, in general, it is difficult to activate technological advancement and that it ultimately remains the result of entrepreneurial initiative and thus that even well-intentioned subventions by the state would possibly impede advancement [24].
13The term entrepreneurship was used by Cantillon around the year 1730 for self-employed merchants who bought goods without knowing at what price they can sell them in the end [25]. Thus, the original meaning referred to risk taking distributors. Around the year 1920, Knight referred to businessmen who relied on changes in the markets and wanted to profit from these changes as entrepreneurs [26]. According to Mandl, entrepreneurial thinking and acting can be operationalized into the following four partial competencies (competence packets): cognitive competencies, motivation related competencies (initiative of one’s own, goal-oriented action), social competencies and organizational competencies [27].
14The growth equilibrium is reached when in the most elementary case, investments and depreciations are balanced. Then, the level of the capital stock per worker will no longer change over a specific period.
15The parameters for the following illustrations are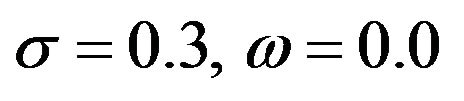 ,
, 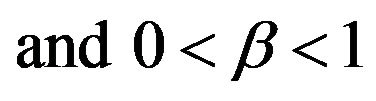
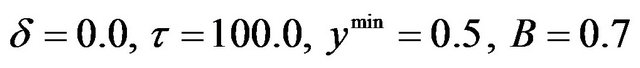 .
.
16Cp. for instance, Schönhofer also uses Lyapunov exponents to characterize attractors and the dynamic behavior of his overlapping generations model “with least squares learning and monotonic savings functions” [29].
17For the explicit calculation of the Lyapunov exponents in this case, see the explanations within the appendix.

