Theoretical Economics Letters
Vol.2 No.5(2012), Article ID:25610,3 pages DOI:10.4236/tel.2012.25080
Some Exact Results for an Asset Pricing Test Based on the Average F Distribution
1School of Economics, Sungkyunkwan University, Seoul, South Korea
2Trinity College, University of Cambridge, Cambridge, UK
3Finance Department, Sydney University, Sydney, Australia
Email: shwang@skku.edu, ses11@econ.cam.ac.uk
Received September 11, 2012; revised October 12, 2012; accepted November 15, 2012
Keywords: Average F distribution; Asset Pricing
ABSTRACT
We provide some exact results for an asset pricing theory test statistic based on the average F distribution. This test is preferred to existing procedures because it deals with the case of more assets than data points. The case mentioned is the practical one that asset managers routinely have to consider.
1. Introduction
The idea of the average F test was first introduced to the literature by [1] as a means of testing asset pricing theories in linear factor models. Recently [2] developed the idea further by focusing on the average pricing error, extending the multivariate F test of [3]. They show that the average F test can be applied to thousands of individual stocks rather than a smaller number of portfolios and thus does not suffer from the information loss or the data snooping biases. In addition, the test is robust to ellipticity. More importantly, [2] demonstrate that the power of average F test continues to increase as the number of stocks increases.
One drawback of the average F test is that [2] did not provide the closed form solution for the average F density function. Despite the fact that the average F statistic has been used in other areas of econometrics, e.g., [4] in the study of structural breaks of unknown timing in regression models, the functional form of the average F distribution remains unknown.
In this study we propose a few analytical developments for the average F distribution. Although the complete functional form is not provided, our results might be useful toward further research in the future.
2. Definition of the Average F Distribution
A testable version of linear factor models is
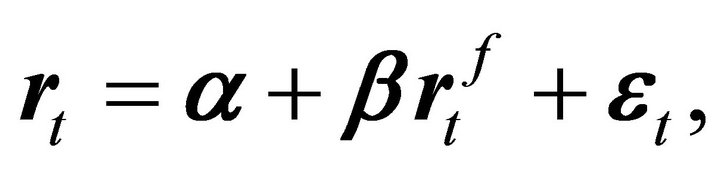 (1)
(1)
where  is a
is a  vector of excess returns for
vector of excess returns for  assets and
assets and  is a
is a 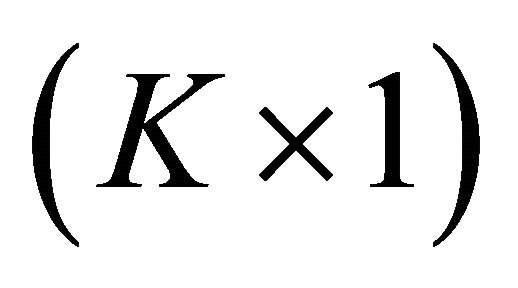 vector of factor portfolio returns,
vector of factor portfolio returns, 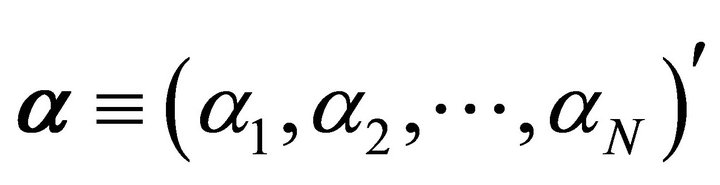 is a vector of intercepts,
is a vector of intercepts,  is an
is an 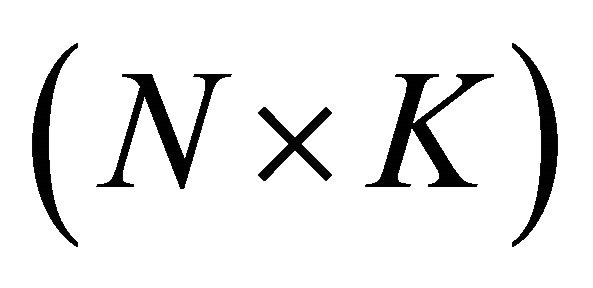 matrix of factor sensitivities, and
matrix of factor sensitivities, and is a
is a  vector of idiosyncratic errorswhose covariance matrix is
vector of idiosyncratic errorswhose covariance matrix is . For the null hypothesis
. For the null hypothesis 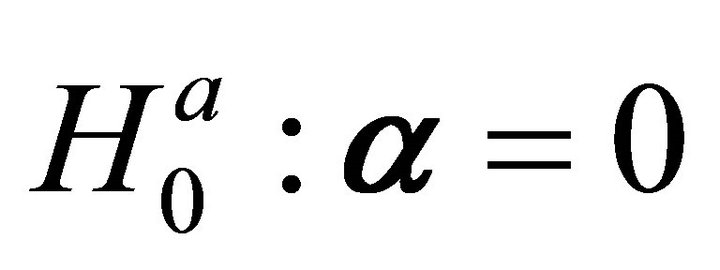 tested against the alternative hypothesis
tested against the alternative hypothesis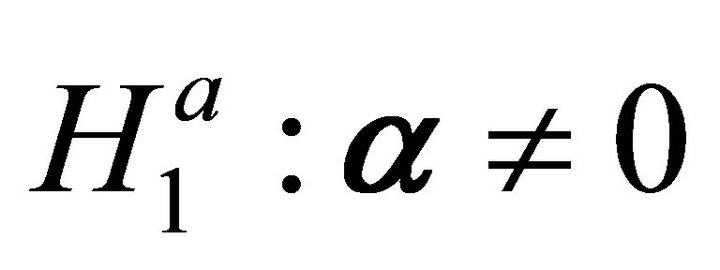 , the average
, the average  -test statistic is defined as
-test statistic is defined as
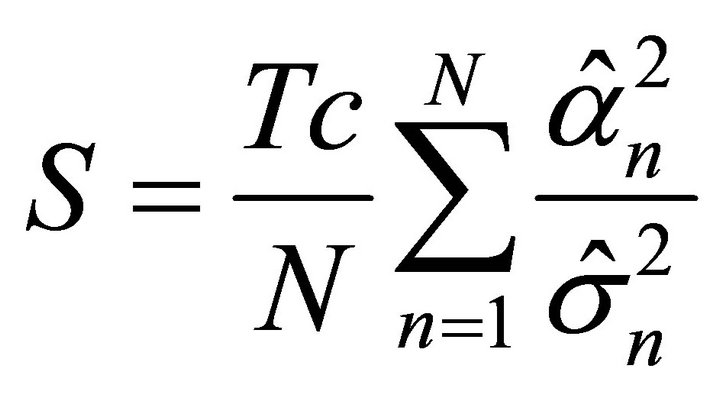 (2)
(2)
where
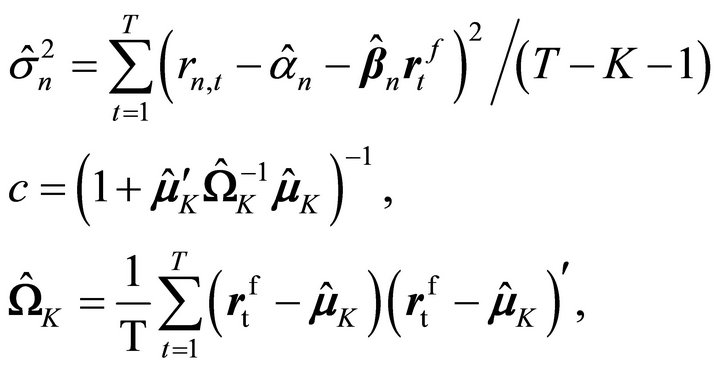
and  and
and 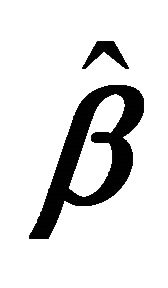 are the maximum likelihood estimators of
are the maximum likelihood estimators of  and
and , respectively. Under the classical assumption that asset returns are multivariate normal conditional on factors, the average F statistic is distributed as
, respectively. Under the classical assumption that asset returns are multivariate normal conditional on factors, the average F statistic is distributed as
 (3)
(3)
where  is a
is a  statistic with 1 degree of freedom in the numerator and
statistic with 1 degree of freedom in the numerator and 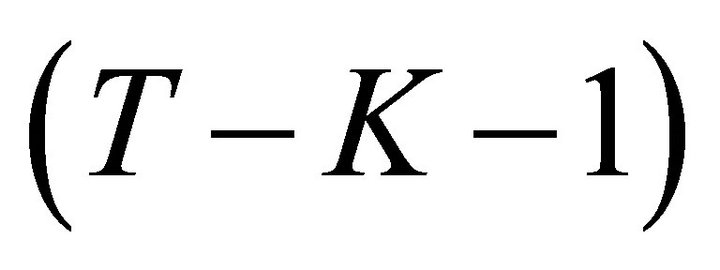 degrees of freedom in the denominator.
degrees of freedom in the denominator.
3. Characteristic Function of the Average F Distribution
The distribution function of the average  statistic is unknown. Note that all
statistic is unknown. Note that all  -distributions in Equation (3) have the same degrees of freedom, and
-distributions in Equation (3) have the same degrees of freedom, and 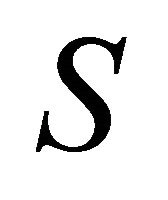 is thus distributed as the sample mean of
is thus distributed as the sample mean of  independent and identically distributed
independent and identically distributed  distributions. Let
distributions. Let 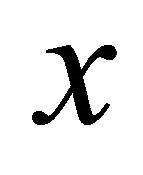 be a variable distributed as
be a variable distributed as , where
, where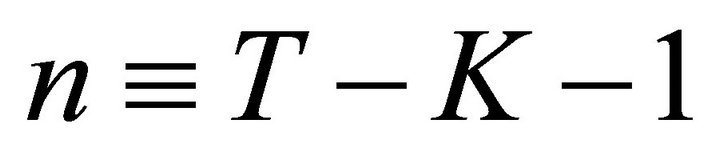 , and denote its probability density function as
, and denote its probability density function as . Then the characteristic function of the
. Then the characteristic function of the  distribution can be derived as follows
distribution can be derived as follows
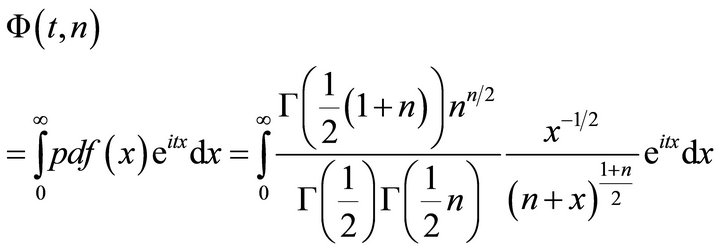 (4)
(4)
Let 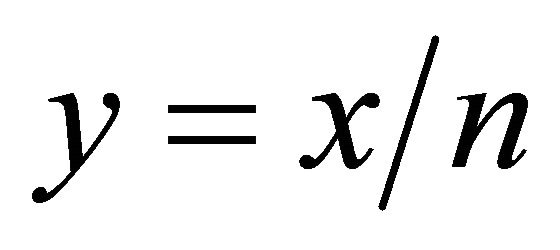 and
and , then
, then
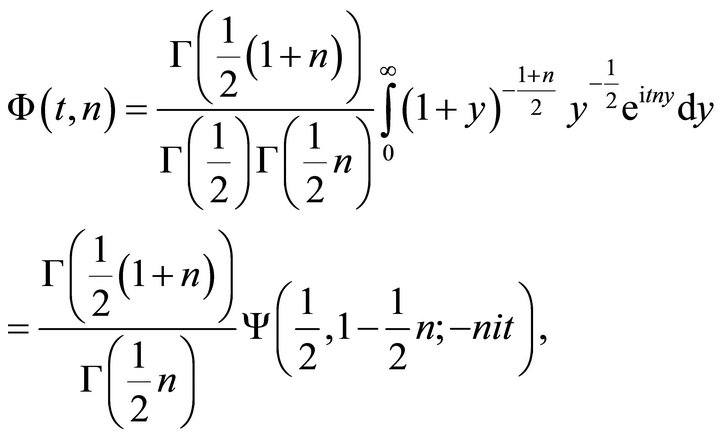 (5)
(5)
where 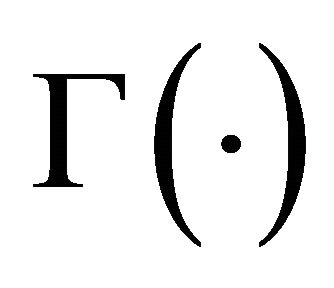 is the gamma function,
is the gamma function,  is the imaginary number, and
is the imaginary number, and  is Tricomi’s confluent hypergeometric function. Equation (5) was first formulated by [5]. Tricomi’s confluent hypergeometric function is
is Tricomi’s confluent hypergeometric function. Equation (5) was first formulated by [5]. Tricomi’s confluent hypergeometric function is
 (6)
(6)
where 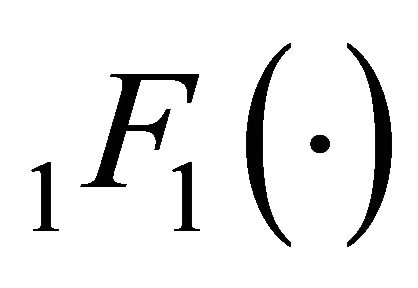 is Kummer’s confluent hypergeometric function which is defined as
is Kummer’s confluent hypergeometric function which is defined as
 (7)
(7)
See [6] for a detailed explanation of various types of hypergeometric functions and their applications to economic theory.
If b in Equation (7) is a non-positive integer, 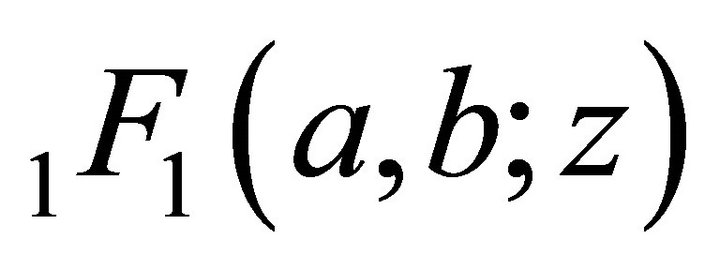 and thus
and thus
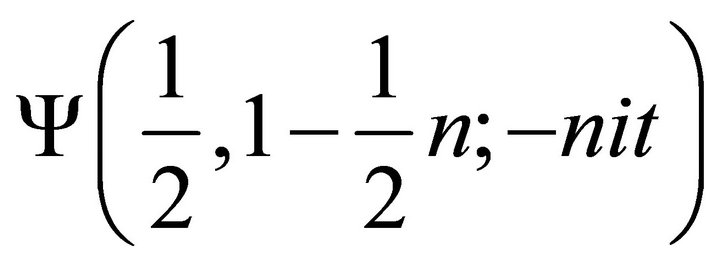
is not defined. Note that 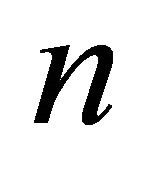 is a positive integer as it represents the degrees of freedom in the denominator of the
is a positive integer as it represents the degrees of freedom in the denominator of the  distribution; thus, we need
distribution; thus, we need
 and
and 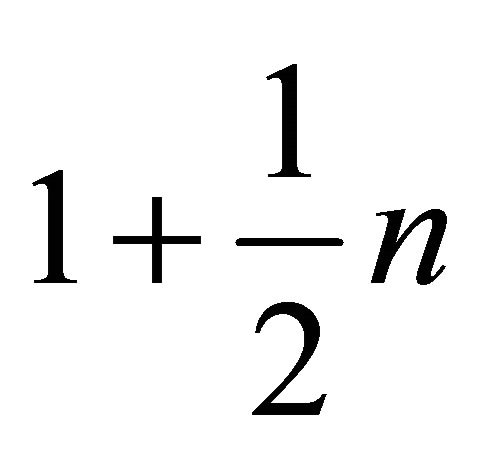
in Equation (6) to be positive integers. However, since n is a positive integer, both
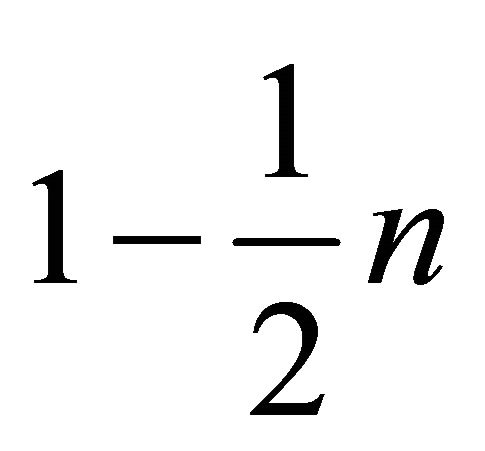 and
and 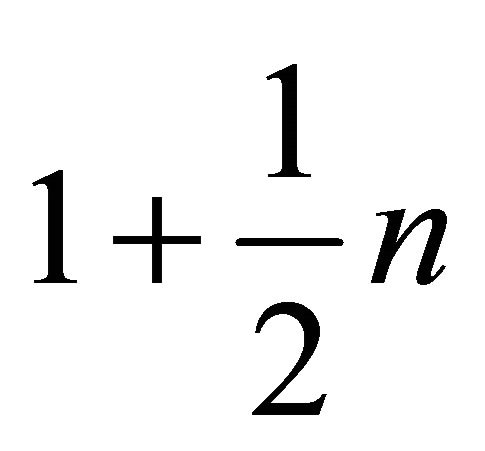
cannot be kept to be positive integers. More generallywhen 
we have a definition referred to as the “logarithmic case” alternative to Tricomi’s confluent hypergeometric function in (6). See [6] and [7] (Vol. 1, pp. 260-262 and Vol. 2, p. 9) for discussions on the logarithmic case.
Let 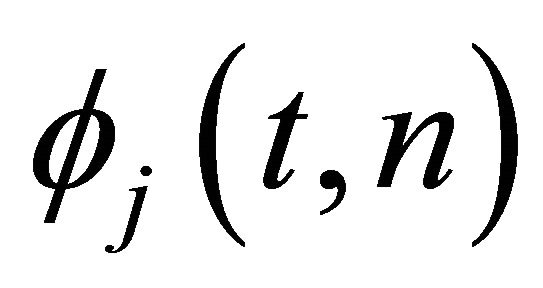 be defined as the characteristic function of the
be defined as the characteristic function of the  independent
independent  variable. Then, the characteristic function of
variable. Then, the characteristic function of  is
is
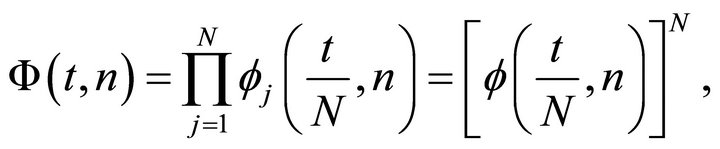 (8)
(8)
where  is defined in (5). Therefore, the density function of the average F statistic
is defined in (5). Therefore, the density function of the average F statistic ,
,  , under the null hypothesis is obtained by the following;
, under the null hypothesis is obtained by the following;
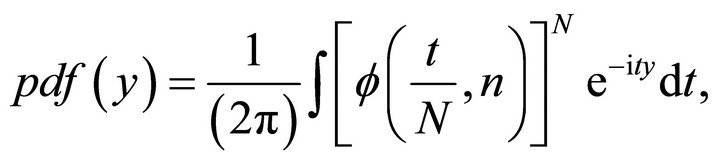 (9)
(9)
where y is a variable distributed as the average of the 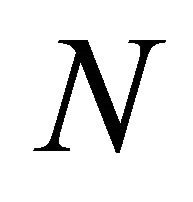 different
different  distributions
distributions This mean of F-distributions can be used when the variance-covariance matrix
This mean of F-distributions can be used when the variance-covariance matrix 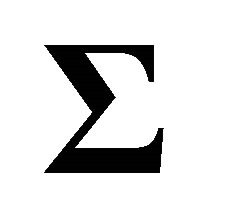 is a diagonal matrix.
is a diagonal matrix.
4. The Exact Distribution of Average F Test for Small N
When , we have
, we have  Using the result that
Using the result that 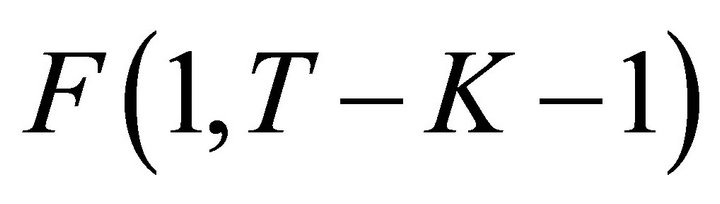 is the square of
is the square of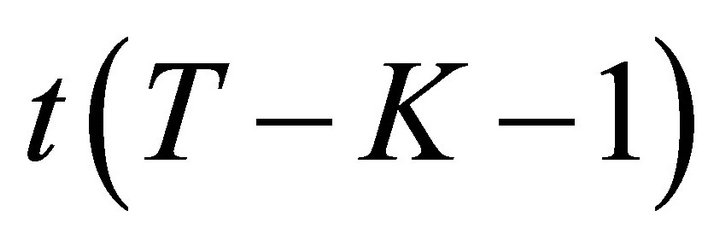 , i.e., a
, i.e., a  distribution with
distribution with  degrees of freedom, we see that the
degrees of freedom, we see that the  of
of 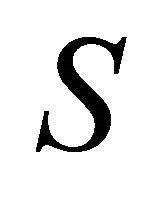 is given by
is given by , letting
, letting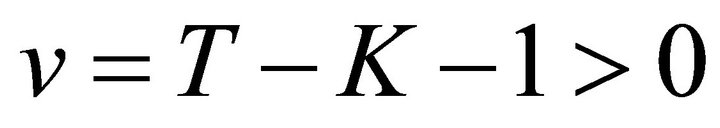 ,
,
 (10)
(10)
where the 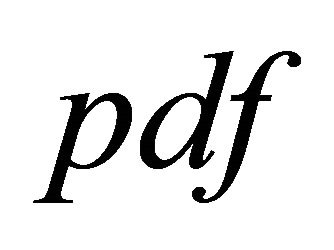 of
of 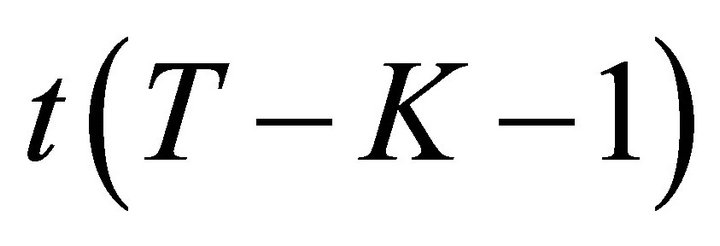 can be found in [8].
can be found in [8].
To find the 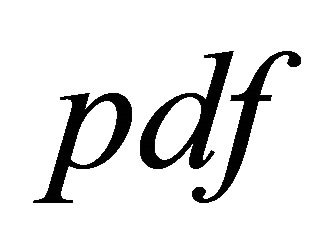 of
of  when
when ,
, 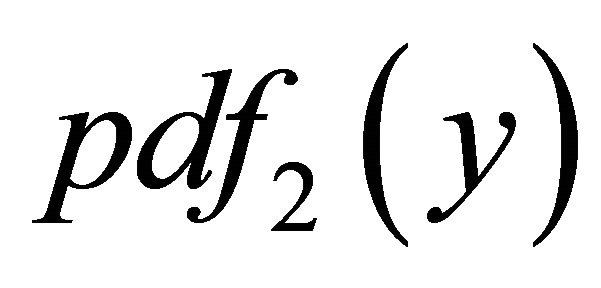 , we proceed as follows. Let
, we proceed as follows. Let  be the associated random variable, and
be the associated random variable, and  and
and  be the two independent
be the two independent 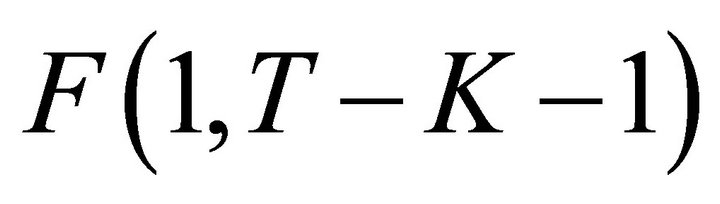 variables. Then we have
variables. Then we have
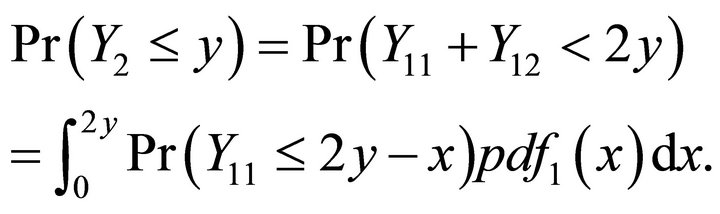
Therefore 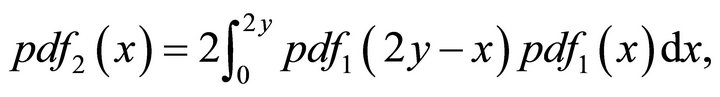
where 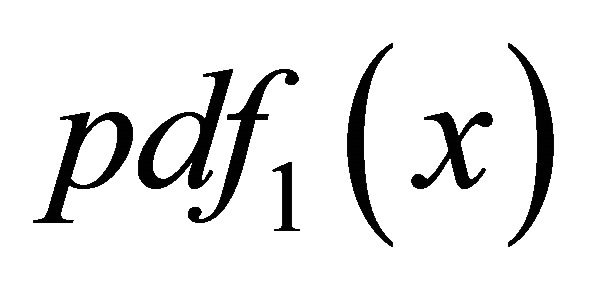 is given by Equation (10). More generally, by induction, it follows that
is given by Equation (10). More generally, by induction, it follows that
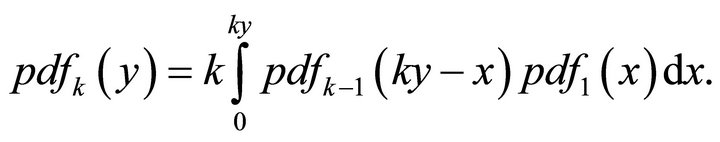 (11)
(11)
Although it is hard to make much progress with Equation (11) in obtaining closed form solutions, we note the following. From known moments of the  distribution, it is possible to calculate the moments of
distribution, it is possible to calculate the moments of 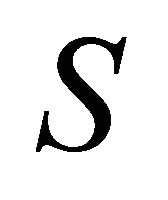 for any
for any , where they exist.
, where they exist.
Proposition 1. The moments of S exist for
 .
.
Proof. Let  Then
Then 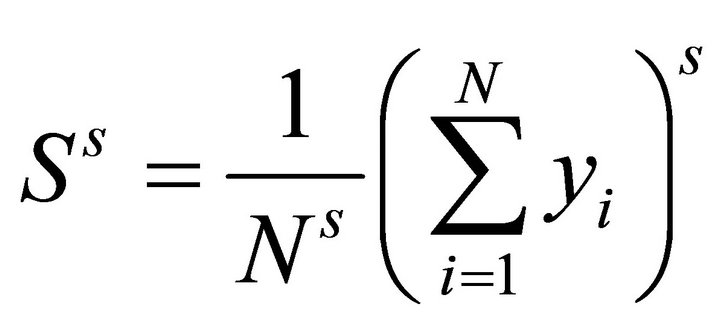
so that the highest order term, for any , is
, is 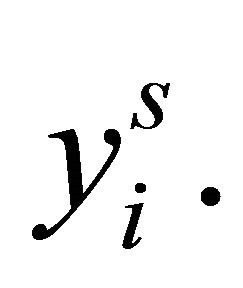 Now from Equation (10),
Now from Equation (10),
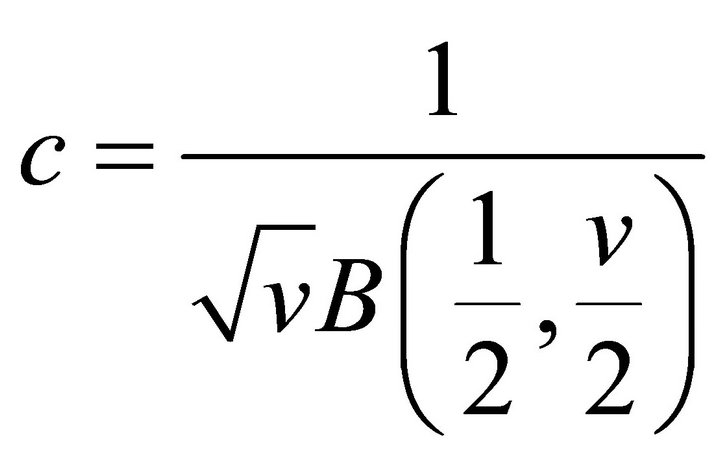 and thus
and thus 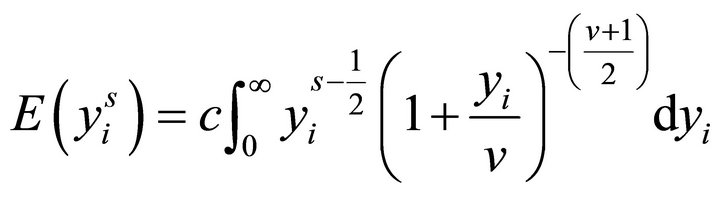 which exists if
which exists if 
Proposition 2 For ,
, 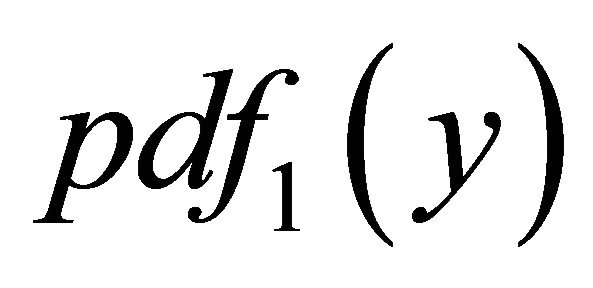 can be represented as a scale Beta type II function.
can be represented as a scale Beta type II function.
Proof. For 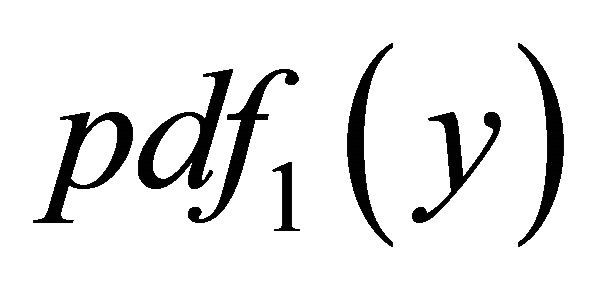 given by Equation (10), let
given by Equation (10), let

Then  and simple change of variable shows that
and simple change of variable shows that  is a Beta
is a Beta 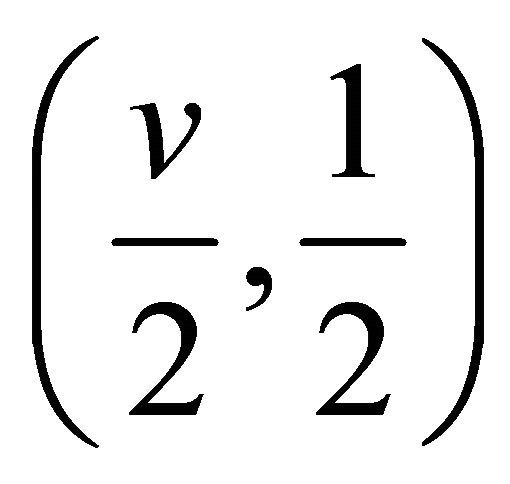 random variable.
random variable.
Since Proposition 2 establishes that  is a scaled Beta, we now have a representation of
is a scaled Beta, we now have a representation of  Denoting
Denoting 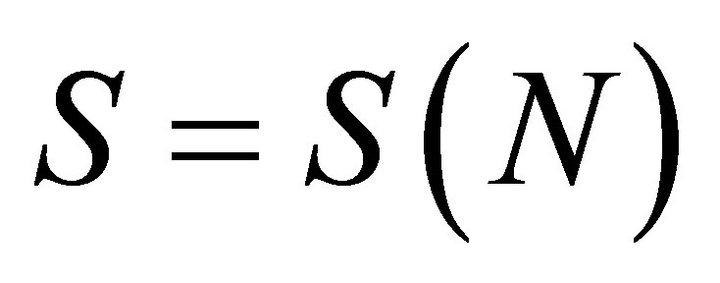 to reflect the dependence on
to reflect the dependence on , it follows from Proposition 2 that
, it follows from Proposition 2 that
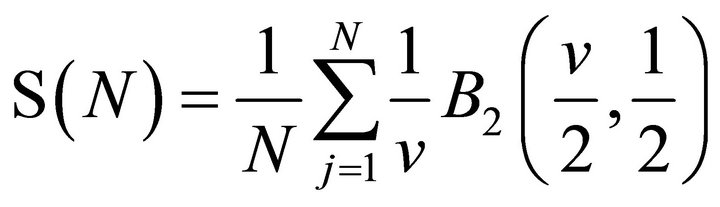 (12)
(12)
where  denotes a type II beta with parameters
denotes a type II beta with parameters ![]() and
and ![]() and the
and the  outside
outside reflects the scale factors. Thus Equation (12) establishes that
reflects the scale factors. Thus Equation (12) establishes that 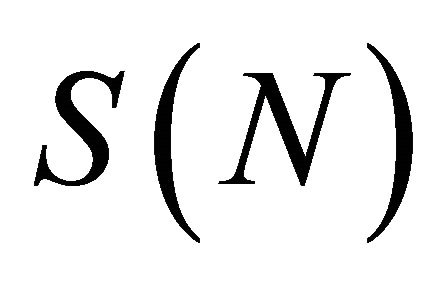 can be represented as a linear combination of Beta type II distributions.
can be represented as a linear combination of Beta type II distributions.
The literature on density functions of linear combination of Beta distributions is rather sparse. [9] present expressions for linear combinations of Beta distributions when . Thus using their results we can arrive at an expression for
. Thus using their results we can arrive at an expression for 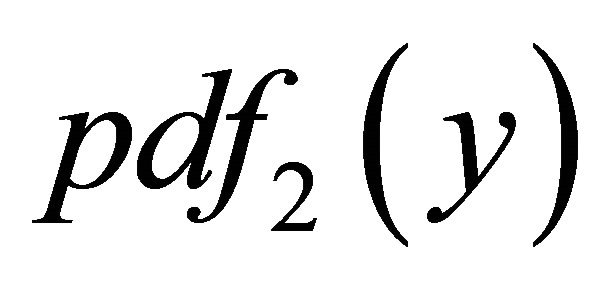 which is complex and depends upon hypergeometric functions. Extensions for
which is complex and depends upon hypergeometric functions. Extensions for 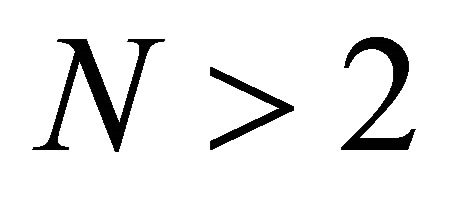 do not appear to be derived as yet.
do not appear to be derived as yet.
5. Conclusion
We provide some developments on the average F test distribution. Although simulation of the statistic is straightforward, an understanding of the functional form is invaluable in terms of appreciation of the properties of the test statistic. We leave a full solution of the problem for future study.
REFERENCES
- J. Affleck-Graves and B. McDonald, “Multivariate Tests of Asset Pricing: The Comparative Power of Alternative Statistics,” Journal of Financial and Quantitative Analysis, Vol. 25, No. 2, 1990, pp. 163-185. doi:10.2307/2330822
- S. Hwang and S. E. Satchell, “Testing Linear Factor Models on Individual Stocks Using the Average F Test,” European Journal of Finance, Forthcoming. doi:10.1080/1351847X.2012.717097
- M. Gibbons, S. Ross and J. Shanken, “A Test of the Efficiency of a Given Portfolio,” Econometrica, Vol. 57, No. 5, 1989, pp. 1121-1152. doi:10.2307/1913625
- D. W. K. Andrew and W. Ploberger, “Optimal Tests When a Nuisance Parameter Is Present Only Under the Alternative,” Econometrica, Vol. 62, No. 6, 1994, pp. 1383-1414. doi:10.2307/2951753
- P. C. B. Phillips, “The True Characteristic Function of the F Distribution,” Biometrika, Vol. 69, No. 1, 1982, pp. 261-264.
- K. M. Abadir, “An Introduction to Hypergeometirc Functions for Economists,” Econometric Review, Vol. 18, No. 3, 1999, pp. 287-330. doi:10.1080/07474939908800447
- A. Erdélyi, “Higher Transcendental Functions,” Mc. GrawHill, New York, 1953.
- A. Stuart and K. Ord, “Kendall’s Advanced Theory of Statistics, Volume 1 Distribution Theory,” 6th Edition, Edward Arnold, London, 1994.
- T. Pham-Gia and N. Turkkan, “Distribution of the Linear Combination of Two General Beta Variables and Applications,” Communication in Statistics; Theory and Methods, Vol. 27, No. 7, 1998, pp. 1851-1869. doi:10.1080/03610929808832194

