ABSTRACT

We investigate the dividend and equity issuance problem in the presence of interest rate. The evolution of the financial reserves of an insurance company, where management payout dividends and issue new equity, is described by a stochastic differential equation. The work of Lokka and Zervos [1] is extended by including the interest rate component into the model in order to make the model more realistic. The aim is to maximise the expected discounted dividends pay-out until the time of bankruptcy. In order to investigate this problem, the stochastic control theory for diffusion processes will be used. In order to handle the problem, the Hamilton-Jacobi-Bellman equation (HJB) is derived and solved. The second order ordinary differential equation associated with the problem turns out to belong to the class of Kummer’s confluent hyper-geometric differential equations. This category of equations is not easy to solve. The equation is non-dimensionalised and change of variables is effected in two different stages. The results show that interest rate affected the rate at which the value function and threshold level change.

Keywords:

Equity Issuance, Optimal Dividend, Hamilton-Jacobi-Bellman Equation, Confluent Hyper-Geometric Function

1. Introduction

The field of stochastic control has evolved a long way from the 1970s, specifically in its application to finance. This is supported by classical works of [2] [3] [4] [5] . The concept of control, from the point of view of mathematics of finance, can be described as the process of influencing the behaviour of a financial system to achieve a desired goal. Stochastic control theory has been applied to design strategies for control of streams of dividends. In the early stages of corporate history, Lintner [5] published work on distribution of dividends as well as retention of earnings for investment purposes which however initiated debate. His classic work constructed a foundation of corporate finance.

Diffusion models for companies that can control their risk exposure by means of their dividend payments have attracted significant interest in the recent years. Komrattanapanya, P. and Suntraruk, P. [6] highlighted that dividend policy has developed into one of the fascinating topics in financial literature today whereas Bistrova and Lace [7] argued that the subject of dividend is insufficiently researched in the emerging countries. On the authority of Dewri and Islam [8] , there are prevailing investor demands for dividend specifically in these emerging countries. Actually, these investors regard dividends as the main component of stock returns [9] , abiding by the theory of bird-in-the-hand where investors inclined towards dividends from stocks to capital gains [10] and [11] .

Miller and Modigliani [2] highly influenced in the development of Dividend Irrelevance Theory. They argued that dividend policy was irrelevant in perfect markets as it had no effect on firm value. According to them, the investor is indifferent between dividend payment and capital gains. However, there is plenty of evidence to support that dividend policy does affect firm value, since Miller-Modigliani assumptions fail to comply with the real-life financial markets. The work of many finance scholars has therefore examined various market imperfections taxes, asymmetric information, agency problems, etc. in order to reflect the importance of dividend policy as well as to determine the optimal dividend policy. Højgaard and Taksar [12] reviewed a model for financial valuation of a firm which has a control of the dividend stream and its risk as well as potential profit by choosing different business activities among those available to it. This model extended the Miller-Modigliani theory of firm valuation, to the situation of controllable business activities in a stochastic environment.

Of late DeAngelo and DeAngelo [13] have questioned MMs irrelevance dividend policy. They indicated that MMs irrelevance theorem compels firms to select only among dividend policies that administer the full present value of free cash flow to shareholders. By the inferred conjecture, distributions at a lower level than the totality of earnings are eliminated. In the opinion of Chang [14] , the MMs first theorem can be substantiated in a setting where financial market for lending and borrowing is absent, with investors and companies not employing identical interest rate. Bailey [15] revealed how the MM-theorem can be proved when capital market is perfect. If an investor is to reproduce the consequences of an economic trend taken by a firm, he must have the capability of borrowing or lending under the same conditions as the firm. As stated by Bailey [15] , the rate of taxation being the same is more significant than taxes being neutral implying that the MMs irrelevance theorem does not automatically fail when taxes vary among financial structure and income source.

Kouki [16] gave theoretical and empirical proof of the significance of payout policy in clarifying the relationship between leverage and the firm value.

Jeanblanc and Shiryaev [17] , Lokka and Zervos [1] and Radner and Shepp [18] respectively, modelled the liquid reserves of a company by means of a Brownian motion with drift, while Asmussen et al. [19] considered more general diffusions.

Taskar and Zhou [20] regarded a model of a corporation, which could choose a business policy among an available set of control policies with different expected profits and associated risks. A choice of the amount of dividends to be paid out to shareholders was also considered. Not withstanding any policy decision there was constant payment of a corporate debt such as bond liability or loan amortization. They showed the existence of an optimal level b₁ such that the optimal dividend policy was to keep the company’s wealth below b₁ and pay-out as dividends all the amounts in excess of this level. The problem is modelled as a mixed classical-singular stochastic control problem, because a company can choose also a production policy.

Asmussen and Taksar [19] studied the optimal dividend policy of a company that tries to maximize the expected value of the dividends received by the shareholders. Liquid assets are modelled as a Brownian motion process with a drift. In the latter of these papers, the company has another control, which is the amount of liquid assets that are risky. Some of the liquid assets can be invested in a risky security. The problem is modelled as a stochastic singular control problem. In Radner and Shepp [18] the firm also chooses parameters of the production process. Choulli, Taksar and Zhou [21] extended some of these results to the case of an insurance company that re-insures some of its risks. Choulli, Taksar and Zhou [22] considered the case in which the drift and the volatility of the liquid assets are related since higher risk implies higher expected return.

Lin He and Zongxia Liang [23] examined an insurance company in which the dividends payout, equity issuance and the risk exposure are controlled by the management. They assumed that the company can only reduce its risk exposure by proportional reinsurance policy for simplicity. The value of the company was associated with the expected present value of the dividend payout minus the equity issuance. Transaction cost was also taken into consideration in the model. The problem was modelled as a mixed singular-regular control problem on diffusion models.

Pierre, E. et al. [24] considered the dividend and investment policies of a cash constrained firm that operate in an environment where equity trading is not feasible but has access to loans. In this situation a firm can raise fund only by issuing collateral debt when it runs out of liquidity. In their study they maximize the shareholders value through dividend and optimal debt issuance. Since by rule, debt cannot directly be used to pay dividend, steadiness in dividend payment is not assured.

Black [25] posed the question again, “Why do corporations pay dividends?” In addition, he posed a second question, “Why do investors pay attention to dividends?” Although, the answers to these questions may appear indisputable, he concluded that they are not. Over two decades after Black’s paper, the dividend puzzle continued. On the other hand, the study by Chevalier, Vath and Scotti [26] examined the problem of determining the optimal control on the dividend and investment policy of a firm. Furthermore, they reviewed the fact that the firm carries a debt obligation in its balance sheet. In conjunction, they considered debt as a means of stimulating investment and in this paper the issuance of equity is considered as a source of funding the firm.

Mtunya A.P., et al. [27] studied on how firm’s management can establish effective investment resolution under the impact of random interest rates. They reflected that interest rate varies steadily and additionally implemented a stochastic discount factor in the optimization of investment level. Their stochastic optimal control was predominantly on investment yet in this paper it it is mainly on dividends and issuance of equity. In the real financial markets, equity issuance is an important approach for a company to earn profit and reduce risk.

Barth, et al. [28] revealed the solutions to several variants of the dividend-distribution problem in a multi-dimensional diffusion setting. They also pointed out that the manager of a corporate must balance the retention of earnings and the distribution of dividends.

They applied dynamic-programming approach, where the state variables are the prevailing levels of cash reserves and of the stochastic short-rate, in addition to time. This developed in a family of Hamilton-Jacobi-Bellman variational inequalities whose solutions were approximated numerically. Mtunya A.P et al. [29] showed how the firms financial management should safeguard a stable dividend payout growth for the shareholders as well as optimizing the dividend policy.

In this study, dividends payout and issuance of equity being done in the presence of transaction costs and interests will be viewed. Despite the fact that a large number of studies have explored issues concerning diffusion models for companies that can control their risk exposure by means of dividend payments, very few results concerned with the inclusion of interest rate component in the diffusion models have been produced. The work of Lokka and Zervos [1] will be extended by including the interest rate component into the model in order to make the model more realistic. The second order differential equation in Lokka and Zervos [1] has a characteristic equation with solutions that consist of exponential functions. The inclusion of such an interest rate component would therefore attract the application of Kummer’s confluent hyper-geometric differential equation, from which the value function is calculated and optimal control is determined. It is mandatory for banks and insurance companies to maintain positive reserves at all times in order to operate. Lokka and Zervos [1] pointed out that, issuance of new equity provides a strategy that can be used by such institutions in meeting their regulatory requirements, ideally in an optimal way.

The uncontrolled reserves dynamics will be modelled by a Brownian motion with drift. Dividend payments and issuance of new equity take the form of “singular” controls. The optimisation problem which corresponds to the maximisation of the performance index J over a set of appropriate admissible dividend and issuance of equity strategies, will be considered. For the resulting optimisation problem leads us to results that have interesting economic interpretations. In this problem, it is optimal to issue minimal new equity so as to reflect the reserves process at 0 and make minimal dividend payments so as to reflect the reserves process at a certain level $x^{\mathrm{<mo>\; *\; </mo>}}$ .

The paper is organised as follows. Section 2 is concerned with the formulation of the stochastic control problem. In Section 3, we work out a solution of Hamilton-Jacobi-Bellman (HJB) equation. The nature of the second order differential equation is transformed into Kummer’s confluent hyper-geometric equation. The solution of the optimal control problem is established that is the optimal value function $V\left(x\right)$ and the corresponding optimal control $u^{\mathrm{<mo>\; *\; </mo>}}$ are derived in this section.

2. Problem Formulation

In order to place the discussion in a rigorous mathematical framework, let $\left(\Omega \mathrm{,}\mathcal{F}\mathrm{,}{\mathcal{F}}_t\mathrm{,}P\right)$ be a filtered probability space satisfying the usual conditions and carrying a standard, one dimensional ${\mathcal{F}}_t$ -Brownian motion ${\left\{W_t\right\}}_{t\ge 0}$ . Consider that an insurance company’s management can control the liquid reserves of the firm by paying out dividends and by raising capital through issuance of equity. The cumulative amount of dividends paid from the initial time $t_0:=0$ up to time t is denoted by $L_t$ , and the total amount raised through issuance of equity from initial time $t_0:=0$ up to time t is denoted by $G_t$ . It is assumed that both the dividend process $L_t$ , and an issuance of equity process $G_t$ are increasing, ${\mathcal{F}}_t$ -adapted processes. Suppose that the reserves $X_t$ , at time t, of the firm, earn interest at a constant rate ρ. Assume that, for no equity issuance and dividend payout the liquid reserves $X_t$ at time t of the company are modelled by the following stochastic differential equation

$\text{d}{X}_t=\left(\mu +\rho X_t\right)\text{d}t+\sigma \text{d}{W}_t\mathrm{,}{X}_0=x\mathrm{.}$ (1)

Given a dividend process $L_t$ and an issuance of equity process $G_t$ , the evolution of liquid reserves of the company is modelled by following the stochastic differential equation

$\text{d}{X}_t=\left(\mu +\rho X_t\right)\text{d}t+\sigma \text{d}{W}_t-\text{d}{L}_t+\text{d}{G}_t,X_0=x,$ (2)

where $x\ge 0$ represents the reserves at time zero, μ and σ are parameters describing the growth rate and the volatility of the reserves process respectively.

Accordingly, we define the bankruptcy time t by

$\tau =\inf \left\{t\ge 0:X_t<0\right\}.$

Following Lokka and Zevos [1] we define the performance functional $J\left(x\mathrm{<mo>\; ;\; </mo>}L\mathrm{,}G\right)$ by

$J\left(x;L,G\right):=E^x\left[\underset{t\to \infty }{\lim }\sup \left({\displaystyle {\int }_{\left[0,t\wedge \tau \right]}}{\text{e}}^{-rt}\text{d}{L}_t-\beta {\displaystyle {\int }_{\left[0,t\wedge \tau \right]}}{\text{e}}^{-rt}\text{d}{G}_t\right)\right],$ (3)

over all admissible controls, $\left(L\mathrm{,}G\right)$ where $E^x$ denotes expectation with respect to P, x represents initial reserves, discount factor r can be the risk free interest rate and the constant $\beta >1$ provides a measure for the transaction costs arising from the issuance of equity. We will denote by $\mathcal{A}\left(x\right)$ as the set of all admissible controls.

The problem is to find the value function V and the corresponding optimal control $u^{*}=\left(L^{*},G^{*}\right)$ such that

$V\left(x\mathrm{,}{x}^{\mathrm{<mo>\; *\; </mo>}}\right)=\underset{\left(L\mathrm{,}G\right)\in \mathcal{A}\left(x\right)}{sup}J\left(x\mathrm{,}L\mathrm{,}G\right)=J\left(x\mathrm{,}{L}^{\mathrm{<mo>\; *\; </mo>}}\mathrm{,}{G}^{\mathrm{<mo>\; *\; </mo>}}\right)\mathrm{.}$ (4)

3. Main Result

At this juncture the problem that arises is addressed. The problem aims at maximising the expected discounted dividend flow minus the expected discounted costs of issuing equity over all dividend and issuance of equity strategies associated with a positive reserves process. The objective of this paper is to find $V\left(x\mathrm{,}{x}^{\mathrm{<mo>\; *\; </mo>}}\right)\mathrm{,0}\le x\le x^{\mathrm{<mo>\; *\; </mo>}}$ . The development was done by employing the same arguments as in [30] . It can be viewed that $V\left(x\mathrm{,}{x}^{\mathrm{<mo>\; *\; </mo>}}\right)$ satisfies he following second order differential equation.

$\frac{1}{2}{\sigma }^2{V}^{″}\left(x,x^{*}\right)+\left(\mu +\rho x\right)V^{\prime }\left(x,x^{*}\right)-rV\left(x,x^{*}\right)=0,0<x<x^{*}$ (5)

with boundary conditions

$\{\begin{array}{l}V\left(0;x^{*}\right)=0\\ V^{\prime }\left(x^{*};x^{*}\right)=1\end{array}$

We can therefore let the function mx represent $V\left(x\mathrm{,}{x}^{\mathrm{<mo>\; *\; </mo>}}\right)$ in (5) yielding the following second-order differential equation

$\frac{1}{2}{\sigma }^2{m}^{″}\left(x\right)+\left(\mu +\rho x\right)m^{\prime }x-rmx=0,x>0$ (6)

with the boundary condition

$m\left(0\right)=0.$ (7)

The second order differential equation has a constant factor Y and unique solution mx and hence from (5)-(7) we can let

$V\left(x^{\mathrm{<mo>\; *\; </mo>}}\mathrm{,}{x}^{\mathrm{<mo>\; *\; </mo>}}\right)=\Psi m\left(x\right)\mathrm{.}$ (8)

Setting $x=x^{*}$ and then differentiating with respect to x to get

$V^{\prime }\left(x^{\mathrm{<mo>\; *\; </mo>}}\mathrm{<mo>\; ;\; </mo>}{x}^{\mathrm{<mo>\; *\; </mo>}}\right)=\Psi m^{\prime }\left(x^{\mathrm{<mo>\; *\; </mo>}}\right)\mathrm{.}$ (9)

Applying $V^{\prime }\left(x^{*};x^{*}\right)=1$ in (6)

$\Psi =\frac{1}{m^{\prime }(x*)}$

hence substituting in (8)

$V\left(x^{*};x^{*}\right)=\frac{m\left(x\right)}{m^{\prime }\left(x^{*}\right)},0\le x\le x^{*}.$ (10)

The first order variable separable equation

$V\left(x;x^{*}\right)=\frac{m\left(x\right)}{m^{\prime }\left(x^{*}\right)}$ (11)

can be reduced to

$m^{\prime }\left(x^{*}\right)V\left(x;x^{*}\right)=m\left(x\right).$ (12)

Integrating both sides with respect to x

${\displaystyle {\int }_{x^{*}}^x}{m}^{\prime }\left(x^{*}\right)V\left(s;x^{*}\right)\text{d}x={\displaystyle {\int }_{x^{*}}^x}m\left(s\right)\text{d}x,$ (13)

yields the following result

$m^{\prime }\left(x^{*}\right)\left(V\left(x;x^{*}\right)-V\left(x^{*};x^{*}\right)\right)=m\left(x\right)-m\left(x^{*}\right)$ (14)

which simplifies to

$V\left(x;x^{*}\right)-V\left(x^{*};x^{*}\right)=\frac{m\left(x\right)}{m^{\prime }\left(x^{*}\right)}-\frac{m\left(x^{*}\right)}{m^{\prime }\left(x^{*}\right)}.$ (15)

But

$V\left(x;x^{*}\right)=\frac{m\left(x\right)}{m^{\prime }\left(x^{*}\right)}$ (16)

which implies that

$V\left(x^{*};x^{*}\right)=\frac{m\left(x^{*}\right)}{m^{\prime }\left(x^{*}\right)}$ (17)

and from (5)-(6)

$V\left(x;x^{*}\right)=x,V\left(x^{*};x^{*}\right)=x^{*},$ (18)

hence substituting these values in (17) results with

$V\left(x;x^{*}\right)=x-x^{*}+V\left(x^{*};x^{*}\right),x>x^{*}.$ (19)

The company’s management takes minimal action to keep the liquid reserves X being below $x^{\mathrm{<mo>\; *\; </mo>}}$ by paying dividends when ever $x>x^{*}$ .

With reference to standard theory of optimal control, the Hamilton-Jacobi-Bellman(HJB) equation corresponding to this problem is given by

$\max \left\{\frac{1}{2}{\sigma }^2{v}^{″}\left(x\right)+\left(\mu +\rho x\right)v^{\prime }\left(x\right)-rv\left(x\right)\beta \right\}=0,x\ge 0$ (20)

combined with the boundary condition

$m\left(0\right)=0.$ (21)

The value function is zero at time $t=0.$

Conjecture―The value function V identifies with a solution m to this HJB equation satisfying the second-order differential equation

$\frac{1}{2}{\sigma }^2{m}^{″}\left(x\right)+\left(\mu +\rho x\right)m^{\prime }\left(x\right)-rm\left(x\right)=0.$ (22)

The nature of the differential equation for the function $m\left(x\right)$ can be transformed into Kummer’s confluent hyper-geometric equation. Firstly we non dimensionalise the equation and then make use of change of variables in two stages. Similar developments were made by [31] but however there are variations in the definition of z. In order to have our calculations as explicit as possible, we need suitable transformations. First of all we define

$z=\frac{\sqrt{2\rho }}{\rho \sigma }\left(\mu +\rho x\right)$ (23)

and the function $f\left(z\right)$ such that $m\left(x\right)=f\left(z\right)$ . Hence

$m^{\prime }\left(x\right)=f^{\prime }\left(z\right)\frac{\text{d}z}{\text{d}x}=\frac{\sqrt{2\rho }}{\sigma }{f}^{\prime }\left(z\right),m^{″}\left(x\right)=\frac{2\rho }{{\sigma }^2}{f}^{″}\left(z\right).$ (24)

Substituting $m\left(z\right)\mathrm{,}{m}^{\prime }\left(z\right)\mathrm{,}{m}^{″}\left(z\right)$ in Equation (22) and simplifying yields the differential equation for $f(z)$

$f^{″}\left(z\right)+s{f}^{\prime }\left(z\right)-\left(\frac{r}{\rho }\right)f\left(z\right)=0,z>\frac{\mu \sqrt{2}}{\sigma \sqrt{\rho }}.$ (25)

In the subsequent stage, accordingly we define $t=-\frac{1}{2}{z}^2$ and the function $h\left(t\right)$ such that $f\left(z\right)=h\left(t\right)$ . Hence

$f^{\prime }\left(z\right)=h^{\prime }\left(t\right)\frac{\text{d}t}{\text{d}z}=-z{h}^{\prime }\left(t\right),f^{″}\left(z\right)=z^2{h}^{″}\left(t\right)-h^{\prime }\left(t\right).$ (26)

Substituting $f\left(z\right)\mathrm{,}{f}^{\prime }\left(z\right)\mathrm{,}{f}^{″}\left(z\right)$ in (24) and simplifying yields the differential equation for the function $h(t)$

$t{h}^{″}\left(t\right)+\left(\frac{1}{2}-t\right)h^{\prime }\left(t\right)-\left(-\frac{r}{2\rho }\right)h\left(t\right)=0,t<-\frac{{\mu }^2}{\rho {\sigma }^2}.$ (27)

The function indeed satisfies the Kummer’s equation of the form

$x\frac{{\text{d}}^{2}y}{\text{d}{x}^2}+\left(c-x\right)\frac{\text{d}y}{\text{d}x}-ay=0$ (28)

with parameters

$c=\frac{1}{2},a=-\frac{r}{2\rho }.$ (29)

The general solution to the hyper-geometric differential equation is

$m\left(x\right)=h\left(t\right)=\alpha {\left(-t\right)}^{1-c}{\text{e}}^{t}M\left(1-a,2-c,-t\right)+\beta {\text{e}}^{t}U\left(c-a,c,-t\right)$ (30)

where

$M\left(a,c,x\right)=z^{1-c}M\left(a-c+1,2-c,x\right),U\left(a,c,x\right)={\text{e}}^{z}U\left(c-a,c,-x\right)$

and

$t=-\frac{1}{2}{z}^2=-\frac{1}{2}{\left(\frac{1}{\rho \sigma }\sqrt{2\rho }\left(\mu +\rho x\right)\right)}^2=-\frac{1}{\rho {\sigma }^2}{\left(\mu +\rho x\right)}^2$ (31)

where a and c are given by (29).

The general solution to the differential equation is given by

$m\left(x\right)=h\left(x\right)=C_{1}p\left(x\right)+C_{2}q\left(x\right),$ (32)

where $C_1$ and $C_2$ are constants and $p\left(x\right)$ and $q\left(x\right)$ are defined by

$p\left(x\right)=z^{1-c}{\text{e}}^{z}M\left(a-c+\mathrm{1,2}-c\mathrm{,}x\right)\mathrm{.}$ (33)

and

$q\left(x\right)={\text{e}}^{z}U\left(c-a\mathrm{,}c\mathrm{,}-x\right)\mathrm{.}$ (34)

Substitute for the values of z, $p\left(x\right)$ and $q\left(x\right)$ in (32).

$m\left(x\right)=C_1{\left(-t\right)}^{1-c}{\text{e}}^{t}M\left(1-a,2-c,-t\right)+C_2{\text{e}}^{t}U\left(c-a,c,t\right)$ (35)

where a and c are given by (29) and

$t=-\frac{1}{2}{z}^2=-\frac{1}{2}{\left(\frac{1}{\sigma }\sqrt{\frac{2}{\rho }}\left(\mu +\rho x\right)\right)}^2=-\frac{1}{\rho {\sigma }^2}{\left(\mu +\rho x\right)}^2.$ (36)

The ratio between α and β follows from the condition that $m\left(0\right)=0$ . We may set

$\alpha =U\left(c-a,c;\frac{{\mu }^2}{p{\sigma }^2}\right),$ (37)

and

$\beta =-{\left(\frac{{\mu }^2}{p{\sigma }^2}\right)}^{1-c}M\left(1-a,2-c;\frac{{\mu }^2}{p{\sigma }^2}\right).$ (38)

Taking derivatives in 30 we obtain

$m^{\prime }\left(x\right)=h^{\prime }\left(t\right)\frac{\text{d}t}{\text{d}x}=-\frac{2^2}{{\sigma }^2}\left(\mu +\rho x\right)h^{\prime }\left(t\right).$ (39)

Using the product rule we obtain

$\begin{array}{c}{h}^{\prime }\left(t\right)=h\left(t\right)-\alpha \left(1-c\right){\left(-t\right)}^{-c}{\text{e}}^{t}M\left(1-a,2c;-t\right)\\ -\alpha \left(\frac{1-a}{2-c}\right){\left(-t\right)}^{1-c}{\text{e}}^{t}M\left(2-a,3-c;-t\right)+\left(c-a\right){\text{e}}^{t}U\left(ca+1,c+1;-t\right).\end{array}$

Finally, we set $x=x^{*}$ in (39) and substitute it and (35) in (11) to obtain $V\left(x\mathrm{<mo>\; ;\; </mo>}{x}^{\mathrm{<mo>\; *\; </mo>}}\right)$ .

Now, considering the time value of money that can lead us to the conclusion that it is optimal to postpone the issuance of new equity for as long as possible. We therefore conjecture that it is optimal to issue equity only when the reserves become zero. Such a conjecture indicates that it is optimal for the company’s management to take no action as long as the reserves process takes values in $\left(\mathrm{0,}{x}^{\mathrm{<mo>\; *\; </mo>}}\right)$ for some $x^{*}>0$ , take the minimal action by issuing new equity so as to prevent the reserves process X from entering $\left(-\infty \mathrm{,0}\right)$ and take minimal action to keep X below $x^{\mathrm{<mo>\; *\; </mo>}}$ . This strategy is associated with a solution to the HJB Equation (20) that is characterised by

$\max \left\{\frac{1}{2}{\sigma }^2{m}^{″}\left(x\right)+\left(\mu +\rho x\right)m^{\prime }\left(x\right)-rm\left(x\right)\right\}=0,x>0.$ (40)

Remark 3.2. In the limiting situation $\sigma =0$ , we have

$\text{d}{X}_t=\left(\mu +\rho X_t\right)\text{d}t-\text{d}{L}_t+\text{d}{G}_t.$ (41)

Multiplying throughout by the integrating factor ${\text{e}}^{-pt}$ resulting with

${\text{e}}^{-\rho t}\text{d}{X}_t-\rho {\text{e}}^{-\rho t}{X}_t\text{d}t=\mu {\text{e}}^{-\rho t}\text{d}t-{\text{e}}^{-\rho t}\text{d}{L}_t+{\text{e}}^{-\rho t}\text{d}{G}_t.$ (42)

Integrating throughout and simplifying to

$X_t=X_0{\text{e}}^{\rho t}+\mu {\text{e}}^{\rho t}{\displaystyle {\int }_0^t}{\text{e}}^{-\rho s}\text{d}s-{\text{e}}^{\rho t}{\displaystyle {\int }_0^t}{\text{e}}^{-\rho s}\text{d}{L}_s+{\text{e}}^{p\rho t}{\displaystyle {\int }_0^t}{\text{e}}^{-\rho s}\text{d}{G}_s$ (43)

Since $X_0=x$ .

$X_t=x{\text{e}}^{\rho t}+{\mu }_0^t{s}_{t^{-}|}^{-}-{\text{e}}^{\rho t}{\displaystyle {\int }_0^t}{\text{e}}^{-\rho s}\text{d}{L}_s+{\text{e}}^{\rho t}{\displaystyle {\int }_0^t}{\text{e}}^{-\rho s}\text{d}{G}_s$ (44)

where $s_{t^{-}\mathrm{<mo>\; |\; </mo>}}^{-}$ is calculated at the force of interest ρ. The determination of $V\left(x\mathrm{<mo>\; ;\; </mo>}{x}^{\mathrm{<mo>\; *\; </mo>}}\right)$ is now an exercise of compound interest. Let $t_0$ be the time when $X\left(t_0\right)=x^{*}$ . Then we find that

$V\left(x;x^{*}\right)={\text{e}}^{-r{t}_0}V\left(x^{*};x^{*}\right).$ (45)

Applying the boundary conditions we have $V\left(x^{*};x^{*}\right)=\frac{\mu +\rho x^{*}}{r}$ hence this simplifies to

$V\left(x;x^{*}\right)={\left(\frac{\mu +\rho x}{\mu +\rho x^{*}}\right)}^{\frac{r}{\rho }}\frac{\mu +\rho x^{*}}{r}.$ (46)

Remark 3.3. When $\rho =0$ the equation takes the form of the Equation (7) in Lokka and Zervos [1] , that is

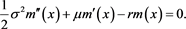(47)

Since the first order linear equation

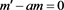(48)

has an exponential function as a solution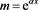. This gives an idea to try as a solution of equation the function

(49)

Substituting (49) in (47) and simplifying to

(50)

where

(51)

Therefore the real numbers are given by

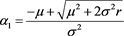(52)

and

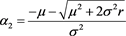(53)

There are two distinct roots 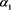and.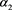

The general solution is therefore

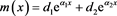(54)

where 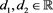are constants.

Since every solution to 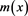that satisfies the boundary condition is associated with the relation. It follows that. From the formula in (16)we get

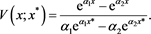(55)

We are then prepared to calculate.

For given, we want to find which maximizes. From (5) and (6) we obtain

From (11) and (12) it follows that

(56)

Hence is positive for small values of. Since for, we gather that attains is maximum for a finite and positive value of. According to (56), the first order condition is that

(57)

It turns out that this equation has a unique solution. Therefore this is the thresh hold which maximizes, independently of x. We note that since

(58)

hence we have

(59)

and from the boundary conditions

(60)

Thus if we set in (9) and use the second condition in (10), we see that

from which it follows that

(61)

The is similar to the present value of a perpetuity, where the payment rate is the sum of the drift and the interest on the initial capital. Equating equation in (9) when to the formula in (55) we have

(62)

This is equivalent to

(63)

For the equation reduces to

(64)

Taking logarithms both sides, simplifies to

(65)

Hence

(66)

The results of this paper are summarised in the following theorem.

Theorem 3.1. For the process given by (1), consider the problem of maximising the profit by (3) over a set of appropriate admissible dividend and issuance of equity strategies. The optimal stopping policy is to issue equity only when the reserves become zero and pay dividends when the liquid cash reaches threshold level of

(67)

with a corresponding value function of

4. Conclusion and Suggestions

Based on the concept of stochastic process, the dividend and equity issuance problem in the presence of interest rate was investigated. The objective was to maximise the expected discounted dividend payments minus the expected discounted costs of issuing new equity. When modelling this problem, the stochastic control theory for diffusion was used with the application of Hamilton-Jacobi-Bellman equation (HJB) dynamic principle. The mathematical formulation of the problem, eventually lead to a stochastic differential problem which belonged to a class of Kummer confluent hyper-geometric equation. However the model studied is not a true description of the real world around us, since corporates or companies are exposed to large, sudden and unpredictable movements in the financial market and other natural disasters like floods, drought and earthquakes. Hence for further research, we can address the optimal dividend and issuance control problem of the insurance company in the presence of interest with jumps.

Acknowledgements

Many thanks goes to the members of JMF for their professional performance, and sincere thanks to managing editor Tammy WU for a unique attitude of exceptional quality.

Cite this paper

Mandiudza, M., Chikodza, E. and Mwareya, N. (2018) Optimal Dividend and Issuance of Equity Policies in the Presence of Interest. Journal of Mathematical Finance, 8, 302-316. https://doi.org/10.4236/jmf.2018.82020

References