Received 25 January 2016; accepted 21 August 2016; published 24 August 2016

ABSTRACT

In this paper, we propose an implementation method for a new concept of stochastic duration which can be used to measure the sensitivity of complex bond portfolios with respect to the fluctuations of the yield surface. Our approach relies on a first order approximation of a chaos expansion in the direction of the yield surface, whose dynamics is described by the Musiela equation. Using the latter technique, we obtain an infinite-dimensional generalization of the classical Macaulay duration, which can be interpreted as the derivative of a first order approximation of a Taylor series on locally convex spaces.

Keywords:

ALM, Risk Management, Interest rate Derivatives, Stochastic Duration, Immunization, SPDE, Musiela Equation

1. Introduction

Asset and liability management (ALM) is the financial risk management of insurance companies, banks and any financial institution. The latter comprises risk assessment in all directions, e.g. policy setting, structuring of the bank’s or insurance’s repricing and maturity schedules, selecting financial hedge positions, capital budgeting, and internal measurements of profitability. Further, it pertains to contingency planning in the sense that the financial institution has to analyze the impact of unexpected changes (e.g. interest rates, competitive conditions, economic growth or liquidity) and how it will react to those changes.

Portfolios managed e.g. by pension funds are usually of high complexity and stochastically depend on the entire term structure of interest rates 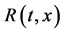or yield surface, dynamically in time. Therefore an accurate risk management of interest rates necessitates the study of stochastic models for interest rates 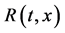in time t and space x (“time-to-maturity”), that is the avarage rate at (future) time t with respect to the time period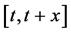, to analyze the interest rate risk and sensitivity of bond portfolios.

One way to model the stochastic fluctuations of the yield surface is based on the so-called Musiela equation, which is a special type of a stochastic partial differential equation (SPDE). In this model (see e.g. [1] ), it is assumed that

where the forward (interest rate) curves 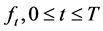satisfy the Musiela equation, and the 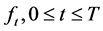is the mild solution to the SPDE

(1.1)

where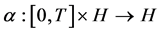, 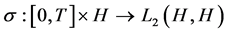are Borel measurable functions and is a cylind- rical Wiener process in H on a filtered probability space

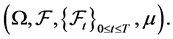(1.2)

Here the filtration is m-completed and generated by W. Further, 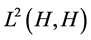denotes the space of Hilbert-Schmidt operators from H into itself.

A crucial aspect of asset liability management is the measurement of the sensitivity and risk analysis of bond portfolios with respect to the stochastic fluctuation of the yield surface. A widely spread method in banks and insurances to measure changes of bond portfolio values with respect to the stochastic fluctuation of the yield surface is the concept of modified duration which was introduced by Macaulay in 1938 [2] . The definition of this concept however is based on the first order Taylor expansion approximation of bond values and requires the unrealistic assumption of parallel shifts of (piecewise) flat interest rates dynamically in time. The latter approach, but also other techniques based on fair prices of interest rate derivatives (see e.g. [3] ), are therefore not suitable for complex hedging portfolios of bonds, since the portfolio weights with respect to the hedged positions usually depend on the whole term structure of interest rates and hence are time-dependent functionals of the (stochastic) yield surface. In order to overcome this problem, one could use the concept of stochastic duration in [4] to measure the yield surface sensitivity of bond portfolios. Here the stochastic duration, which can be considered a generalization of the classical duration of Macaulay, is defined as a Malliavin derivative in the direction of the (centered) forward curve 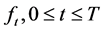in the Musiela Equation (1) under a certain change of measure and con-

ditions on the filtration.

Since the concept of stochastic duration, which enables a more accurate interest rate management and which could be e.g. used to devise new premium calculation principles for life insurance policies with “stochastic” technical interest rates, it is necessary to develop numerical methods or approximation schemes for its estimation.

In this paper we aim at proposing a numerical approach to estimate the stochastic duration in [4] in the more general setting of mild solutions to (1.1) by using a first order chaos expansion approximation of bond portfolio values as functionals of the forward curve. This idea is in line with the classical Macaulay definition of duration and corresponds to a first order Taylor series approximation on locally convex spaces in infinite dimensions (see e.g. [5] ). This approximation may be also compared to the approach of Jamshidian [6] with respect to the stochastic modeling of large multi-currency portfolios by means of a Gaussian distribution as an application of the central limit theorem. In this context it is worth mentioning that the second order chaos expansion approximation of the bond portfolio value, which gives a more realistic portfolio modeling and which we don’t consider in this paper, actually corresponds to the application of a non-central limit theorem (see [7] ).

Furthermore, using the above techniques we want to generalize the concept of immunization strategies for bond portfolios as introduced in [8] to the case of non-flat stochastic interest rates.

The paper is organized as follows:

In Section 2 we pass in review some basic facts from infinite dimensional interest rate modeling and Malliavin calculus for Gaussian fields. Moreover, adopting the ideas in [4] we introduce the concept of sto- chastic duration in the setting of mild solutions to (1.1).

Finally, in Section 3 we want to discuss an implemention method for the estimation of stochastic duration and the concept of portfolio immunization strategies.

2. Framework

We recall in this section some mathematical preliminaries.

Consider the SPDE

(2.1)

where A is the generator of a strongly continuous semigroup on H, ,

are Borel measurable functions, is a cylindrical Wiener process in H

on a filtered probability space. We need the following concept of solution to (2.1).

Definition 2.1. (Mild solutions) An -adapted process on is said to be a mild solution to (2.1) if (see [9] ):

1)

2), and

3) for all, m-a.s.,

(2.2)

Remark 2.2. If the coefficients and in (2.1) satisfy the Lipschitz condition

for a constant, then there exists a unique mild solution to (2.1). Moreover, for all we have that

for a constant.

In the sequel, we choose H to be the following weighted Sobolev space (see [1] ).

Definition 2.3. Let be an increasing function such that

Then the space defined as

is a Hilbert space with the inner product

The space exhibits the following important properties which we want to use throughout the paper:

1) The evaluation functional

is a continuous linear functional.

2) The integration functional

is a continuous linear functional.

3) The differential operator is the generator of the strongly continuous semigroup given by the left

shift operator defined by

for.

In what follows, we assume that.

In order to rule out arbitrage opportunities, we shall also require that the drift coefficient in (2.1) satisfies the following generalized Heath-Jarrow-Morton (HJM) no-arbitrage condition (see [1] ):

in, where is a sequence of predictable (risk premium) processes

and where for an orthonormal basis of.

Assuming that is always invertible, we may rewrite (2.2) as

(2.3)

where

By the infinite-dimensional Girsanov theorem, which can be applied if e.g. the Novikov condition

holds, there exists a measure, equivalent to, under which

is a cylindrical Wiener process.

In the following, we shall also require that for all Thus, in this case the centered forward curve given by

becomes a centered Gaussian random field in time t and time-to-maturity under r.

We shall also assume the following condition. There exists a unique strong solution to the SDE

The latter condition in connection with the properties of the left shift operator and the diffusion coefficient actually ascertains that the filtrations generated by and coincide. Using the above con- ditions, we can now introduce the concept of stochastic duration as a Malliavin derivative with respect to the centered forward curve.

2.1. Malliavin Calculus for Gaussian Fields

We now define the Skorohod integral and Malliavin derivative with respect to the Gaussian process, according to [10] . Let be a centered Gaussian process on, let be the covariance function of, and let be the reproducing kernel Hilbert space (RKHS) of C. Moreover, let be the closed linear subspace of spanned by. If, there is a unique element such that

Definition 2.4. (First-order stochastic integral)

is an isometry of into, and is called the stochastic integral of order one. In order to define higher-order integrals, let be an orthonormal basis in. Because of isometry it is sufficient to define for functions of the form

Definition 2.5. (Higher-order stochastic integral) Let be the distinct elements of

. For, let be the number of times the element was repeated in the sequence, and

define

where is the pth Hermite polynomial.

For every integer, let be the symmetric tensor product of p copies of K.

Lemma 2.6.

Proof. This is Lemma 2.4 in [10] .

Theorem 2.7. (Chaos decomposition) It follows that every random variable V in this -space may be expressed as an infinite sum

where. This representation is known as the chaos decomposition of V with respect to f.

Now let V be a process in. For every p, let now be a function in, such that for every t, and such that for all t (is symmetric in the first p variables),

Definition 2.8. (Skorohod integral) If converges in, this sum is defined as

the Skorohod integral of V with respect to the Gaussian process f and is denoted by.

Lemma 2.9. if and only if

and in this case

Proof. This is Lemma 3.3 of [10] .

Definition 2.10. (Malliavin derivative) For an element of, if

the process given by is in and we have (see [10] ):

In this case we say that G is Malliavin differentiable, and we call the Malliavin derivative of G, with respect to the Gaussian process.

Definition 2.11. (Stochastic duration) Let G be a square integrable functional of the centered forward curve with respect to the risk-neutral measure. Assume that G is Malliavin differentiable with respect to. Then the stochastic duration of G is the random field given by

Remark 2.12. The Malliavin derivative D can indeed be regarded as a sensitivity measure with respect to the stochastic fluctuations of the (centered) forward curve. The latter, however, is a consequence of the relationship

between the Malliavin derivative and stochastic Gateaux K-derivative (see [10] ): If and if

(2.4)

converges in as for, then DG exists and the limit in (2.4) coincides with. The probability measures and are equivalent. Therefore we may interpret DG for a portfolio value G at time T as a sensitivity measure with respect to the stochastic non-linear shifts of the (centered) yield surface.

We may also be interested to derive an estimate of the instantaneous movement of the portfolio value as a “directional derivative” given by the scalar product

By substituting different curves for we may get an overview of the effects on the portfolio of the various possible outcomes of the short-term movements of interest rates at different parts of the maturity spectrum. This method exhibits a radically increased degree of flexibility as compared to the classical method of Hull and White, where one was restricted to the study of flat or piecewise-flat interest rates, and the dependence on time-to-maturity was not taken into account. In the next Section, we will describe a method of estimating the stochastic duration from market data, and then extend to our setting the method of Hull and White [8] of constructing immunization strategies, which facilitate the reduction of interest-rate related risk by dynamically rebalancing the portfolio with instruments which counteract the interest-rate sensitivity measured by duration.

3. Computation of Stochastic Duration and Immunization Strategies

3.1. Implementation Scheme for the Stochastic Duration

Consider now a square integrable adapted (portfolio) process. Then it follows from Theorem 2.7 that

(3.1)

In the next step, we aim at approximating the chaos decomposition in (3.1) by the first homogeneous chaos, that is we assume that

where is a real number. On the other hand, it follows from the definition of stochastic integrals with respect to and the properties of the left shift operator that

for continuous linear functionals on with

for all. Hence, using Girsanov’s theorem, we get that

under the original probability measure. Denote by an orthonormal basis of. Then, we finally approximate

by

where denotes the k-the component of W. So our numerical estimation scheme will rely on the stochastic process

where is a one-dimensional Wiener process.

On the other hand, by using the HJM-condition, we may similarly approximate the drift coefficient by

for.

In the following, let us assume that is the volatility function of the one-dimensional Vasicek model for short rates, that is

where is the mean reversion and the volatility.

Applying the Malliavin operator to the approximating process yields a first-order approximation of the duration

The task is then to estimate the functional. We take as input the observed portfolio values at a series of time points, which correspond to in our model.

To allow numerical implementation, we shall assume that is absolutely continuous. Further, we

shall introduce a discretized version of the functional:

(3.2)

where is absolutely continuous and is given by

for bounded and measurable functions. Recall that is the evaluation functional for.

Furthermore, we approximate and the weak derivative of by step functions:

Hence, using our assumptions, we see that

(3.3)

where

and

We now need to derive some quantity from the model process Z which takes scalar values and may be compared to observable market data. A natural candidate is the quadratic variation

By applying integration by parts in connection with (3.3) to

we get that

where

and where is a continuous adapted bounded variation process. So it follows that

(3.4)

The observation from market data, which corresponds to, is approximately

for.

However, in practice observations of are noisy, i.e. we have

(3.5)

where is a one-dimensional Wiener process independent of, and

(3.6)

In order to estimate the parameters and from market data, we employ nonlinear filtering theory. See e.g: [11] and the references contained therein for more information on nonlinear filtering theory.

In applying nonlinear filtering techniques, we assume that the observation process is given by (3.5) and the observation function by (3.6). Set for convenience.

Further, suppose that the signal process has components satisfies the SDE

where is independent of.

We may here for convenience assume that is a vector of i.i.d variables which are e.g. uniformly or normally distributed. In what follows we want to determine the optimal filter

where is the filtration generated by the observation process, and where,

is a Borel measurable function.

It follows from the Kallianpur-Striebel formula (see e.g. [11] ) that

(3.7)

where

and where is a Wiener process independent of under a Girsanov transform Q.

Since is independent of under Q we get the representation

(3.8)

where denotes a probability measure with respect to on a separate sample space.

The latter however enables us to use Monte Carlo techniques, i.e. the strong law of large numbers to approximate (3.8) by

(3.9)

for “large” R, where are i.i.d. copies of and where

By choosing projections for f in (3.9) in connection with (3.7) we finally obtain filter estimates for the parameters.

We implemented the method in MatLab and as an illustration we reproduce in Figure 1 a plot of the resulting duration surface from a simulation example with fictional market data and.

3.2. Delta Hedge

Using our implementation scheme for the stochastic duration, we finally want to discuss portfolio immunzation strategies against interest rate risk based on the so-called delta-hedge, which was studied in [8] in the case of piecewise flat interest rates. Our aim is to generalize the concept of a delta hedge for piecewise flat interest rates to the case of stochastic yield surfaces based on the above implementation scheme. To this end, consider a bond portfolio with value at time point. We now want to hedge against the fluctuations of the yield surface by constructing a delta hedge by means of interest rate derivatives (e.g. swaps, caps, bond options, …) with values

The delta hedge corresponds to the adapted stochastic process such that

for all.

For convenience, let us now assume that is a deterministic process. Then we see that

(3.10)

Since in general there is no strategy satisfying (3.10), one may resort to the following minimization problem:

Now, using our implementation scheme, we can regard as deterministic functions and obtain the following optimization problem

Here one may choose the optimization constraint given by

for all and some.

4. Conclusion

In the paper [4] where the concept of duration under discussion was originally introduced, the emphasis was on the theoretical construction which did not straightforwardly lead to numerical results. We have here adapted the model to yield a computationally tractable numerical algorithm. This shows that stochastic duration is a potentially useful tool in practical risk analysis. Moreover we indicate how the method can be employed to immunization of portfolios against interest rate risk, which lends further support to this conclusion. More work is needed on the implementation of the method on realistic market data, and it would be interesting to extend the method to incorporate the effects of higher-order terms in the chaos expansion, especially the second-order term which corresponds to the concept of convexity.

Cite this paper

Sindre Duedahl, (2016) Implementation of Stochastic Yield Curve Duration and Portfolio Immunization Strategies. Journal of Mathematical Finance,06,401-415. doi: 10.4236/jmf.2016.63032

References

Appendix

Submit or recommend next manuscript to SCIRP and we will provide best service for you:

Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.

A wide selection of journals (inclusive of 9 subjects, more than 200 journals)

Providing 24-hour high-quality service

User-friendly online submission system

Fair and swift peer-review system

Efficient typesetting and proofreading procedure

Display of the result of downloads and visits, as well as the number of cited articles

Maximum dissemination of your research work

Submit your manuscript at: http://papersubmission.scirp.org/