Journal of Mathematical Finance
Vol.05 No.02(2015), Article ID:55502,9 pages
10.4236/jmf.2015.52011
On a New Index Aimed at Comparing Risks
Marina Resta, Maria Erminia Marina
DIEC, University of Genova, Genova, Italy
Email: resta@economia.unige.it
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 January 2015; accepted 7 April 2015; published 10 April 2015
ABSTRACT
This paper fits into the research stream started by Aumann and Serrano (2008) with their index RAS, and introduces a new index of riskiness called Iθ. In particular, our intuition moves from the observation that the RAS index is defined over the set of gambles whose expected value of losses is lower than the one of gains. We then restrict the attention on investment opportunities in a proper relation with a benchmark value  and we build the index Iθ. The mathematical features of the new index are discussed in deepest detail, providing evidence that Iθ can be used by the investor in comparing risks: θ plays the role of a threshold value such that once fixed in the range
and we build the index Iθ. The mathematical features of the new index are discussed in deepest detail, providing evidence that Iθ can be used by the investor in comparing risks: θ plays the role of a threshold value such that once fixed in the range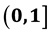 , Iθ suggests to take into consideration a gamble (an investment, an asset) g only if the ratio between the expected value of its losses and the expected value of its gains is lower than such θ. Moreover, Iθ nests RAS as special case when θ = 1, and it satisfies both homogeneity and duality properties. In the light of these features, Iθ seems to satisfy the common need among practitioners for flexible index of riskiness.
, Iθ suggests to take into consideration a gamble (an investment, an asset) g only if the ratio between the expected value of its losses and the expected value of its gains is lower than such θ. Moreover, Iθ nests RAS as special case when θ = 1, and it satisfies both homogeneity and duality properties. In the light of these features, Iθ seems to satisfy the common need among practitioners for flexible index of riskiness.
Keywords:
Index of Riskiness, Threshold Value, Losses/Gains Ratio

1. Introduction
Riskiness is a key issue in a broad number of situations, spanning from finance to insurance and economics. The first attempt to quantify risk is contained in [1] [2] and [3] . These authors introduced the mean-standard deviation approach as a method to reduce risk, while maintaining the expected return at a desired level. Their contributions initiated a very fruitful research which over the past sixty years developed in two main directions [4] : on one hand, by investigating the ways to quantify how much risky a situation is, as well as to establish whether or not a situation is riskier than another; on the other hand, by discussing the way to evaluate whether an agent is more risk adverse than another. With respect to the first issue, [5] [6] gave fundamental contributions on stochastic dominance, while the second problem was independently faced by [7] and [8] , who pionereed the theory of risk aversion. However, the very basic knot remains how to put such research streams into practice. Known attempts towards this route date back to earlier seventies, with their ups and downs: the use of deviation measures [9] to analyze risky assets is an example. Indeed, some of them (like the standard deviation) may be very inadequate for aiding the investor’s decision making process. Consider, for instance, two risky assets (gambles) X1 and X2: while X1 equally assures either a gain of $600 or a loss of $500, X2 gives the investor equal probability either to gain $700 or to lose $490. Clearly X2 gives lower losses and higher gains than X1. Nevertheless, X2 is the gamble with higher standard deviation: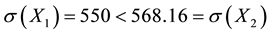 . The unsuitability of classical deviation measures has been the boost engine to promote the study of more sophisticated measure like Value at Risk ?VaR? [10] [11] and Conditional Value at Risk ?CVaR? [12] [13] . In particular, VaR proved to have superior qualities than variance/standard deviation; on the other hand, CVaR owns superior mathematical properties than VaR (it is a coherent risk measure), but it is sometimes more difficult to be implemented [14] .
. The unsuitability of classical deviation measures has been the boost engine to promote the study of more sophisticated measure like Value at Risk ?VaR? [10] [11] and Conditional Value at Risk ?CVaR? [12] [13] . In particular, VaR proved to have superior qualities than variance/standard deviation; on the other hand, CVaR owns superior mathematical properties than VaR (it is a coherent risk measure), but it is sometimes more difficult to be implemented [14] .
A new path is now coming from the research vein started in 2008 by Aumann and Serrano [15] who developed a monotone1 measure of riskiness that a decision maker can use to compare gambles. Suppose a gamble g to be a random variable with positive expected value and positive probability of negative values; [15] say that in presence of such a gamble g, an agent with utility function u accepts it at wealth w if: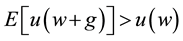 . Aiming to rank gambles and decide whether a gamble is more risky than another, they then developed the index of riskiness RAS which associates to every gamble g the value
. Aiming to rank gambles and decide whether a gamble is more risky than another, they then developed the index of riskiness RAS which associates to every gamble g the value 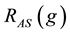 that is the unique positive solution of the equation:
that is the unique positive solution of the equation: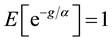 . The index RAS exhibits a number of very appealing features, such as monotonicity with respect to first order stochastic dominance, and positive homogeneity; moreover it makes possible to reach a complete ordering of all considered gambles. However, the most important feature of the RAS index mainly relates to the duality axiom, which essentially requires that if a gamble is accepted by an investor, less risk averse investors accept less risky gambles. In this light, this is an economically motivated axiom, and therefore rightly Aumann and Serrano claimed their RAS index to be an economic index of riskiness. With this background, the work of Aumann and Serrano may be straightforwardly considered a very inspiring contribution that has shown many lines towards which address future research efforts. A first element of innovation, for instance has been kept by [16] who introduced the measure of riskiness RFH: whereas RAS orders gambles (investments) looking at the utility function regardless of wealth, RFH examines the investments looking for the critical wealth regardless of utility. Extensions towards this direction include the contributions of [17] who show how to extend the definition of RFH to continuous random variables and to dynamic environments; [18] extends the definition of acceptance dominance order to risky assets whose values follow random processes, and using differential calculus shows that the acceptance dominance order is a complete order that can be represented by an index of local risk. On the other hand, [19] working on the original RAS concept, studied an extension of the stochastic dominance order, which is equivalent to the one introduced by the index of Aumann and Serrano. Moreover, [20] suggested an alternative axiomatic characterization for the RAS index. More recently [21] discussed a class of measures, which nests RAS as a special case, and allows riskiness to be examined relative to benchmark levels of (net) return other than zero: it is also provided empirical evidence that the ordering of two financial assets in terms of their relative riskiness may vary even with only small changes in the benchmark level of return. Another interesting contribution is that of [22] who developed a risk normalization procedure for Aumann-Serrano riskiness that has the two-fold aim to turn contradictory rankings into coherent ones, and to combine the effects of correlation and outliers into the analysis. On this basis, they deduce functional connections among performance measures, deriving a new indicator which expresses performance as the addition of three effects due to Sharpe Ratio [23] [24] , correlation and outliers. Finally, [25] highlighted that both RAS and RFH were created with a risky world in mind, but not an uncertain one; starting from this point, decision under uncertainty is modeled and a complete and objective rankings of sets of gambles is obtained, which extends the previous riskiness measures.
. The index RAS exhibits a number of very appealing features, such as monotonicity with respect to first order stochastic dominance, and positive homogeneity; moreover it makes possible to reach a complete ordering of all considered gambles. However, the most important feature of the RAS index mainly relates to the duality axiom, which essentially requires that if a gamble is accepted by an investor, less risk averse investors accept less risky gambles. In this light, this is an economically motivated axiom, and therefore rightly Aumann and Serrano claimed their RAS index to be an economic index of riskiness. With this background, the work of Aumann and Serrano may be straightforwardly considered a very inspiring contribution that has shown many lines towards which address future research efforts. A first element of innovation, for instance has been kept by [16] who introduced the measure of riskiness RFH: whereas RAS orders gambles (investments) looking at the utility function regardless of wealth, RFH examines the investments looking for the critical wealth regardless of utility. Extensions towards this direction include the contributions of [17] who show how to extend the definition of RFH to continuous random variables and to dynamic environments; [18] extends the definition of acceptance dominance order to risky assets whose values follow random processes, and using differential calculus shows that the acceptance dominance order is a complete order that can be represented by an index of local risk. On the other hand, [19] working on the original RAS concept, studied an extension of the stochastic dominance order, which is equivalent to the one introduced by the index of Aumann and Serrano. Moreover, [20] suggested an alternative axiomatic characterization for the RAS index. More recently [21] discussed a class of measures, which nests RAS as a special case, and allows riskiness to be examined relative to benchmark levels of (net) return other than zero: it is also provided empirical evidence that the ordering of two financial assets in terms of their relative riskiness may vary even with only small changes in the benchmark level of return. Another interesting contribution is that of [22] who developed a risk normalization procedure for Aumann-Serrano riskiness that has the two-fold aim to turn contradictory rankings into coherent ones, and to combine the effects of correlation and outliers into the analysis. On this basis, they deduce functional connections among performance measures, deriving a new indicator which expresses performance as the addition of three effects due to Sharpe Ratio [23] [24] , correlation and outliers. Finally, [25] highlighted that both RAS and RFH were created with a risky world in mind, but not an uncertain one; starting from this point, decision under uncertainty is modeled and a complete and objective rankings of sets of gambles is obtained, which extends the previous riskiness measures.
Moving to practical applications, [26] proved that the implicit equations used to solve for the indexes can be naturally interpreted as moment conditions for the Generalized Method of Moments (GMM) estimation [27] . In addition, [28] provide both theoretical and empirical investigations to address the connection between portfolio and ordering theory, with the focus on the properties of risk measures, variability measures, and tracking-error measures. Operative interpretations of RAS were also provided independently one to each other in [29] and (a bit later) in [30] , who found out that RAS is the reciprocal of the adjusting coefficient that is used in the insurance risk literature as a proxy to monitor the risk of going bankruptcy. Moreover, [31] observed that although the RAS index was proposed for gambles in terms of absolute outcomes, it can be applied to excess returns, since the latter can be regarded as the outcome of a zero investment strategy that consists in borrowing $1 and investing it in a risky asset for a given time span. Furthermore, [31] [32] discussed the use of RAS on different bunches of mutual and hedge funds, comparing the results to those obtained with more standard risk measures. Finally [33] and [34] applied RAS to the lower tail of investment returns thus developing a new measure of pertinent risk for risk-averse investors.
Our paper contributes to the related literature by proposing an index of riskiness in the route of that of Aumann and Serrano: we consider gambles 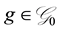 that have positive expectation and can take some negative value, because this is the interesting case: indeed a random variable
that have positive expectation and can take some negative value, because this is the interesting case: indeed a random variable 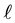 with
with 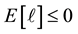 is rejected by every risk-averse decision maker; at the same time, a non-trivial random variable
is rejected by every risk-averse decision maker; at the same time, a non-trivial random variable 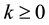 is accepted by every decision maker. Our intuition moves from the observation that the RAS index is defined over the set of gambles
is accepted by every decision maker. Our intuition moves from the observation that the RAS index is defined over the set of gambles 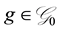 with positive expectation: this is equivalent to say that RAS ranks the gambles whose expected value of losses
with positive expectation: this is equivalent to say that RAS ranks the gambles whose expected value of losses 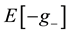 is lower than the one of gains
is lower than the one of gains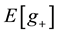 . We also recall that [35] link the availability of attractive investment opportunities to the Gain/Loss ratio: for example a Gain/Loss ratio of two means that the investor receives twice as much gain as would be necessary to increase his holdings in the asset; likewise, he risks only half the loss that he would be willing to accept to increase his holdings. We then assume that the investor is interested to evaluate the attractiveness of investments when the ratio
. We also recall that [35] link the availability of attractive investment opportunities to the Gain/Loss ratio: for example a Gain/Loss ratio of two means that the investor receives twice as much gain as would be necessary to increase his holdings in the asset; likewise, he risks only half the loss that he would be willing to accept to increase his holdings. We then assume that the investor is interested to evaluate the attractiveness of investments when the ratio 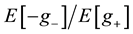 maintains lower than a fixed threshold value
maintains lower than a fixed threshold value . Once fixed a level
. Once fixed a level 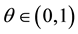 the investor could pick up from the original set
the investor could pick up from the original set 















Thereafter, what remains of the paper is organized as follows. Section 2 introduces and describes the basic features of the Aumann and Serrano model. Sections 3 presents some preliminary concepts useful from a mathematical viewpoint to introduce our index of riskiness. This latter is derived in Section 4. Section 5 concludes.
2. The Aumann-Serrano (AS) Model: A Brief Review
Following [15] , any investor takes his decision depending on two basic factors: 1) how risky the gamble is, and 2) how averse the individual is to risk. From a formal point of view, the first factor depends only on the probabilistic features of the gamble, while the second one is related to the investor’s utility function.
Consider a probability space

Denote by 

Moreover, an investor is characterized by a utility function in the Von Neumann-Morgenstern sense [36] , that is 










Within this framework, provided that 
An agent with utility function u accepts the gamble g at wealth w if:

In order to compare gambles and decide whether a gamble is more risky than another, define an index Q to be a mapping that assigns a positive real number to each gamble g: [15] proposed two axioms that an index should satisfy. The first is duality: given two gambles g and h and two agents characterized by the utility functions u and v, respectively, such that u is uniformly no less risk averse than v (i.e.:




Thus a CARA agent

Roughly, former properties characterize RAS in an axiomatic way. The duality axiom gives a mathematical interpretation of the following fact: provided two agents, one uniformly no less risk averse than the other, this latter will take a fortiori a position less riskier (according to the newly introduced index) than that one the former agent will consider. In addition, the homogeneity axiom embodies the cardinal nature of riskiness, making possible to quantify it. More precisely, it makes sense to say that if g is a gamble, then 2g is not only riskier than g but it as twice as risky as g.
To conclude, RAS suggests by way of the duality and homogeneity axioms an order for gambles, but from an operational point of view, one might be tempted to ask more, for instance by requiring stronger conditions to either accepting or rejecting a risky asset. Keeping this in mind, in next sections we work on the hypotheses (1) and (2), hence modifying the original model of Aumann and Serrano.
3. Generalizing the RAS Index: Preliminary Settings
Using the notational conventions we already introduced in Section 2, we now consider the following definition.
Definition 3.1 Let



where:


By construction, in (4) we examine the ratio between the decrement in the expected utility due to all possible outcomes of 


In order to discuss some mathematical features of R, we preliminary recall that g first order stochastically dominates on h if and only if:

where Fg, Fh are the cumulative distribution functions of g and h, respectively. We now introduce a theorem establishing for every utility function u and every wealth w how the measure 
Theorem 1 Assume:


Proof. We set:

that gives:


If 




and:
and we can conclude.
Another interesting feature of R relates to its behaviour under monotone transformations of the investor’s utility function. We summarize this result in Theorem 2.
Theorem 2 Consider two utility functions





Proof. We have:

iff:

Let:
and:
By Fubini’s theorem, (10) is equivalent to:

As u1 is a [strictly] concave and increasing transformation of u2, we have:

with:
Note that for all 





Remark 3.1 Given two utility functions u1, u2, corresponding to investors i1 and i2 respectively, by the Arrow-Pratt theorem we get: 


Consider now two CARA agents


Now, for every gamble g and for every 

Assuming a CARA agent with wealth w and utility function

Then, we can introduce the following theorem.
Theorem 3 For every gamble 


and:
Proof. From (14) it follows that 

In a similar fashion:

4. Acceptance and the Index of Riskiness
We are now ready to introduce our index of riskiness
Definition 4.1 Consider an agent with utility function u, wealth


otherwise the agent rejects g at the level θ.
Remark 4.1 From (13), if for a gamble g we have:
Let us now illustrate Definition 4.1 with an example.
Example 4.1 Let us set to zero the initial wealth:













Note that by Theorem 2, assuming 






Assume now a CARA agent, a gamble


has a unique solution iff:

Now, we define the set:

and for all 

As the function 









Example 4.2 Let us consider the gambles g and h already employed in the Example 4.1. The equation: 



Table 1 and Table 2 report the values of 





We are now going to introduce a number of mathematical features shared by the 





Assume



Table 1. Values of
Table 2. Values of
Furthermore:
Theorem 4 Consider two gambles g, h, being

・ 
・ 
Proof. Assume

Moreover, by (13), given two gambles g, h it is:


Finally, since 

However, the most important property of the index 
Theorem 5 Let two gambles 




then:

Proof. By hypothesis and by Theorem 2 we have:

therefore by Theorem 3 we have:



Theorem 5 posits a duality statement. In fact, it says that given two gambles g and h and two agents such that the first one is uniformly no less risk averse than the other, if the first agent with wealth w accepts g at the threshold θ, and 
5. Conclusions
In this paper we presented a new index of riskiness that we obtained using the index of Aumann and Serrano (2008) as starting point, and having in mind the Gain/Loss ratio of [35] as well.
In particular, our intuition moved from the observation that the RAS index is defined over the set of gambles whose expected value of losses is lower than the one of gains. In practical applications, however, the investor could be more demanding, restricting the attention on investment opportunities in a proper relation with a benchmark value θ: we assumed that 







Nevertheless, some issues need to be addressed. In particular, the risk framework we discussed in this paper still stays on the theoretical stage. Future research efforts will move basically towards two directions, by deriving efficient computational algorithms to calculate it, and by discussing some simulations studies, in order to compare 
References
- Markowitz, H.M. (1952) Portfolio Selection. The Journal of Finance, 7, 77-91. http://dx.doi.org/10.2307/2975974
- Markowitz, H.M. (1959) Portfolio Selection: Efficient Diversification of Investment. Yale University Press, New Haven.
- Roy, A. (1952) Safety First and the Holding of Assets. Econometrica, 20, 431-449. http://dx.doi.org/10.2307/1907413
- Laffont, J.J. (1993) The Economics of Uncertainty and Information. MIT Press, Cambridge.
- Haddar, J. and Russel, W.R. (1969) Rules for Ordering Uncertain Prospects. American Economic Review, 59, 25-34.
- Rothschild, M. and Stiglitz, J. (1970) Increasing Risk: A Definition. Journal of Economic Theory, 2, 225-243. http://dx.doi.org/10.1016/0022-0531(70)90038-4
- Arrow, K.J. (1951) Alternative Approaches to the Theory of Choice in Risk-Taking Situations. Econometrica, 19, 404-437. http://dx.doi.org/10.2307/1907465
- Pratt, J. (1964) Risk Aversion in the Small and in the Large. Econometrica, 32, 122-136.
- Rockafellar, R.T., Uryasev, S. and Zabarankin, M. (2006) Generalized Deviations in Risk Analysis. Finance and Stochastics, 10, 51-74. http://dx.doi.org/10.1007/s00780-005-0165-8
- J. P. Morgan (1996) Risk Metrics Technical Document. Morgan Guarantee Trust Company.
- Pflug, G.C. (2000) Some Remarks on the Value-at-Risk and the Conditional Value-at-Risk. In: Uryasev, S.P., Ed., Probabilistic Constrained Optimization: Methodology and Applications, Kluwer, Norwell, 278-287. http://dx.doi.org/10.1007/978-1-4757-3150-7_15
- Artzner, P., Delbaen, F., Eber, J.M. and Heath, D. (1999) Coherent Measures of Risk. Mathematical Finance, 9, 203- 228. http://dx.doi.org/10.1111/1467-9965.00068
- Rockafellar, R.T. (2007) Coherent Approaches to Risk in Optimization under Uncertainty. INFORMS Tutorials in Operations Research, Institute for Operations Research and the Management Sciences, Hannover, 38-61.
- Dowd, K. (2005) Measuring Market Risk. The Wiley Finance Series # 323.
- Aumann, R. and Serrano, R. (2008) An Economic Index of Riskiness. Journal of Political Economy, 116, 810-836. http://dx.doi.org/10.1086/591947
- Foster, D.P. and Hart, S. (2009) An Operational Measure of Riskiness. Journal of Political Economy, 117, 785-814. http://dx.doi.org/10.1086/644840
- Riedel, F. and Hellmann, T. (2015) The Foster-Hart Measure of Riskiness for General Gambles. Theoretical Economics, 10, 1-9. http://dx.doi.org/10.3982/TE1499
- Schreiber, A. (2013) Comparing Local Risk by Acceptance and Rejection. Mathematical Finance, Published Online. http://dx.doi.org/10.1111/mafi.12054
- Hart, S. (2011) Comparing Risks by Acceptance and Rejection. Journal of Political Economy, 119, 617-638. http://dx.doi.org/10.1086/662222
- Foster, D.P. and Hart, S. (2013) A Wealth-Requirement Axiomatization of Riskiness. Theoretical Economics, 8, 591- 620. http://dx.doi.org/10.3982/TE1150
- Bennett, C.J. and Thompson, B.S. (2013) Moving the Goalposts: Subjective Performance Benchmarks and the Aumann-Serrano Measure of Riskiness. Working Paper, SSRN Electronic Journal. http://dx.doi.org/10.2139/ssrn.2247023
- Bosch-Badia, M.T., Montllor-Serrats, J. and Tarrazon-Rodon, M.A. (2014) Unveiling the Embedded Coherence in Divergent Performance Rankings. Journal of Banking & Finance, 42, 154-165. http://dx.doi.org/10.1016/j.jbankfin.2014.01.015
- Sharpe, W.F. (1966) Mutual fund performance. The Journal of Business, 39, 119-138. http://dx.doi.org/10.1086/294846
- Sharpe, W.F. (1994) The Sharpe Ratio. The Journal of Portfolio Management, 21, 49-58. http://dx.doi.org/10.3905/jpm.1994.409501
- Michaeli, M. (2014) Riskiness for Sets of Gambles. Economic Theory, 56, 515-547.
- Kadan, O. and Liu, F. (2011) Performance Evaluation with High Moments and Disaster Risk. Working Paper. http://ssrn.com/abstract=2020724
- Hansen, L.P. (1982) Large Sample Properties of Generalized Method of Moments Estimators. Econometrica, 50, 1029- 1054. http://dx.doi.org/10.2307/1912775
- Ortobelli, S., Rachev, S.T., Shalit, H. and Fabozzi, F.J. (2013) Portfolio Selection Problems Consistent with Given Preference Orderings. International Journal of Theoretical and Applied Finance, 16, Article ID: 1350029.
- Meilijson, I. (2009) On the Adjustment Coefficient, Drawdowns and Lundberg-Type Bounds for Random Walk. The Annals of Applied Probability, 19, 1015-1025. http://dx.doi.org/10.1214/08-AAP567
- Homm, U. and Pigorsch, C. (2012) An Operational Interpretation and Existence of the Aumann-Serrano Index of Riskiness. Economic Letters, 114, 265-267. http://dx.doi.org/10.1016/j.econlet.2011.10.030
- Homm, U. and Pigorsch, C. (2012) Beyond the Sharpe Ratio: An Application of the Aumann-Serrano Index to Performance Measurement. Journal of Banking and Finance, 36, 2274-2284. http://dx.doi.org/10.1016/j.jbankfin.2012.04.005
- Shalit, H. (2011) Measuring Risk in Israeli Mutual Funds: Conditional Value-at-Risk vs. Aumann-Serrano Riskiness Index. Working Paper, Ben-Gurion University of the Negev, Beersheba.
- Kauffmann, A., Shalit, H. and Zahavi, G. (2012) Profit Index―Pertinent Risk of Financial Investment. Working Paper. http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2190841
- Shalit, H. (2013) On Pertinent Risk. Working Paper, Ben-Gurion University of the Negev., Beersheba.
- Bernardo, A.E. and Ledoit, O. (2000) Gain, Loss and Asset Pricing. Journal of Political Economy, 108, 144-172.
- Von Neumann, J. and Morgenstern, O. (1944) Theory of Games and Economic Behavior. Princeton University Press, Princeton.
NOTES
1With respect to stochastic dominance.
2This assumption can be relaxed; see for instance [30] .
3Constant Absolute Risk Averse.
4i.e.: provided that the index of riskiness of g at the threshold value θ is greater than the index of riskiness of h at the threshold level θ, then the second one accepts h at the level θ if its wealth is equal to w.













