Received 21 January 2015; accepted 9 February 2015; published 11 February 2015

ABSTRACT

We investigate the implications of time inconsistent preferences on the entrepreneurial decision making. We use a time varying preference model to capture the optimal liquidation choice and investment allocation for the averse risk agent in the incomplete market. Compared to standard entrepreneurial dynamic framework, our model shows that inconsistent preferences may lead to under investment when the entrepreneur faces liquidity constraint and over investment when his liquid wealth is far away from the liquidation boundary. Moreover, the possibility of changing to the future stage has ambiguous influences on the exit decision and optimal investment.

Keywords:

Time Inconsistency, Liquidity Constraints, Precautionary Saving, Optimal Liquidation, Investment Strategy

1. Introduction

Entrepreneurs face high uncertainty and liquidity constraints, both of which have significant influences on the business decision making process. These uncertainty and constraints are important determinants for capital ac- cumulation, exit decision and asset allocation. Since [1] , the real option approach has become an essential part of optimization problem for the entrepreneurs. [2] develop an incomplete-market q-theoretic model to study entrepreneurship dynamics and find that the illiquidity, idiosyncratic risks and borrowing constrains result in business decisions, consumption and asset allocation decisions different with the standard complete markets profit-maximizing analysis for entrepreneurial firms.

In the standard optimization model framework, it is assumed that agents have a constant rate of time pre- ference. However, virtually every experimental research on time preference indicates that this assumption is unrealistic. The most relevant effect of time inconsistent is the preference change with time. Usually, an agent has different preferences at different stages. In this article, we focus on the entrepreneurs’ decision making under non-constant preference.

In our paper, we try to focus on the following interesting questions: What is the impact of time inconsistent preference on the entrepreneurial valuation? How could the time varying discount rate affects the liquidation choices? How would the entrepreneur allocate the wealth between investment, consumption and public equity? We extend the entrepreneurial optimization model in [2] by incorporating the time inconsistence preferences.

Our model gives three main contributions. First, the time inconsistent agent will under invest when his liquid wealth is close to liquidation boundary and over invest when the agent is far away from the exit threshold. Second, time inconsistent preferences weaken the effects of risk aversion on the liquidation decisions. Third, increasing the possibility of the birth of the future stage with utility discount has ambiguous influences on the exit decision and investment strategy and finally the decisions approach the steady result in the future stage.

Our research relates to the literature about time inconsistency model and its application. [3] models time varying impatience with quasi hyperbolic discount functions and explains why consumers have asset-specific marginal propensities. [4] describe the equilibrium of a discrete-time exchange economy in which consumers with arbitrary subjective discount factors and homothetic period utility functions follow linear Markov consumption and portfolio strategies. [5] consider two types of goods: goods with immediate costs and delayed benefits, and goods with immediate benefits and delayed costs. With time inconsistency model, they explain how to design optimal contract respond to consumer biases. [6] extend the real option framwork to model the investment timing decisions of entrepreneurs with time inconsistent preferences.

The remainder of the paper proceeds as follows: Section 2 presents the model; Section 3 derives the solutions; Section 4 provides the quantitative results and Section 5 concludes.

2. Model

In this section, we set out the framework for the basic model of entrepreneurial optimization problem. The liqui- dation option is described and followed by a discussion of the nature of time inconsistent preferences.

Time is continuous and horizon is infinite. There is a single perishable consumption good. The agent derives utility from a consumption process 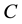according to

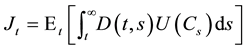(1)

where 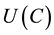is a concave function. For tractability, we choose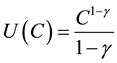, where 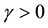is the coefficient

of relative risk aversion. 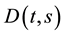denotes the agent’s intertemporal discount function: the agent’s value at time of $1 received at the future time s. We thus have

(2)

for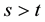. As in [7] , the present stage could last for a random duration of time. For simplicity, we assume that the lifespan of present agent 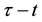is exponentially distributed with parameter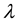. Stated in another way, the birth of future agent is modeled as a Poisson process with intensity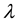. We defin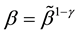e where 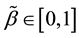measures the degree of the agent’s utility discount in future stage. We assume the agent is in the present stage, and thus the value function is:

(3)

Consider the setting for a standard entrepreneurial problem as in [2] . The agent possesses a firm and our pro- duction specification features the widely used “AK” technology augmented with capital adjustment costs. Let I denote the gross investment. The change of capital stock 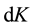is given by:, where is the rate of depreciation. The firm’s productivity shock over the period is independently and identically distributed (iid), and is given by:, where is a standard Brownian motion, and are the mean and volatility of the productivity shock respectively. The firm’s operating revenue over period is proportional to and is given by. The firm’s operating profit over the same period is given by:

(4)

where is the adjustment cost. We assume that the firm’s adjustment cost is homogeneous of degree one in and, and write in the homogeneous form as:, where

is the firm’s investment-capital ratio. For simplicity, we assume, where the parameter

measures the degree of the adjustment cost.

The entrepreneur has an option to liquidate capital at any moment. Liquidation is irreversible and gives a terminal value, where is a constant. Let denote the optimal liquidation time. When the entre- preneur is not well-diversified, liquidation provides an important channel to manage the downside risk exposure.

The agent can invest in risk free asset and public equity. These two financial asset represent the standard investment opportunities in the classical [8] model. The risk free asset accumulates with a constant interest rate. Incremental return of public equity, , over time period is iid: , where is a standard Brownian motion, and are the constant expected mean and volatility, respectively. The sharp

ratio for the public equity is:. Let denote the correlation coefficient between the public equity

and the entrepreneurial business. The non diversifiable risks play a role in the decision making process.

Let be the amount allocated to the risky public equity at time, and denote the liquid financial wealth process. Before, the agent holds the firm and acts as an entrepreneur. The liquid financial wealth process evolves as follows:

(5)

After exiting from the business, the agent retires and accumulates in the following form:

(6)

The agent is allowed to borrow against capital at all times in our model. To make sure the debt is risk free, we set the liquidation value of the capital greater than outstanding debt:

(7)

The optimization problem of the agent involves the maximization of the utility defined as (3). First, before liquidation, the entrepreneurial objective is to choose a consumption process, a portfolio allocation rule, the investment process and an optimal liquidation timing strategy to maximize the utility subject to the wealth dynamics (5) and borrowing constrain (7). After the liquidation option has been exercised, the entrepreneur collects the liquidation proceeds and retires. And then the agent chooses optimal allocation between the risk free asset, public equity and consumption.

3. Solution

3.1. Benchmark: Time Consistent Preference

As a benchmark, we consider the case in which the entrepreneurial preference is time consistent. The constant preference case reduces to [2] , and the solution to this problem is summarized in Proposition 1.

Proposition 1. The entrepreneur operates the business if and only if. Before liquidation the entrepreneurial value function is given by, where

. The scaled certainty equivalent (CE) wealth solves

the following ordinary differential equation (ODE):

(8)

where and. When approaches,

approaches the complete-markets solution given by, where is the scaled average q in complete-market:

(9)

The ODE (8) satisfies the following boundary conditions at endogenous liquidation choice: and. The optimal consumption, investment and the public equity allocation-

capital ratio are given by:, and

. After exiting entrepreneurship, the agent’s value function takes the following homothetic form:

3.2. Time Inconsistent Case

Consider the case of an entrepreneur who makes decisions under the belief that future selves act in the interest of the current self. This assumption has been analyzed in [9] . In addition, this assumption is also consistent with empirical evidence on 401 (K) investment (see [10] ), and health club attendance (see [11] ).

Assume the entrepreneur is in the present stage where the value function takes the form as (3). The standard dynamic programming argument implies that the agent’s optimal consumption, investment and public equity allocation solve the following Hamilton-Jaobi-Bellman (HJB) equation of value function:

(10)

where is the value function in time consistence case. It is easy to verify that takes the form:

(11)

Let denote the entrepreneurial endogenous liquidation boundary and. The following pro- position summarizes the solution for the optimal decisions making and scaled CE wealth.

Proposition 2. The scaled CE wealth solves the following ODE:

(12)

When approaches, approaches the complete-market solution given by

, where measures the influence of time inconsistence preference on

the valuation in complete-market. is the solution to the following function:

. The ODE (12) satisfies the following conditions at the endogenous

optimal liquidation choice: and.

The consumption, investment and public equity allocation are given by,

and. After the liquidation, the agent’s value function takes the form:.

4. Quantitative Results

Parameter choices. Where possible, we borrow the parameters from [2] . We set. For public equity, and. Adjusted cost and depreciation. For production shock, and. Capital liquidation price.

4.1. Optimal Liquidation Boundary

Figure 1 plots the effects of risk aversion and correlation on liquidation boundaries. Panel A presents in different levels of. [2] study the effects of risk aversion in time consistent case and find that a higher entrepreneur will exit earlier. We find the trend stays the same in time inconsistent case while the liquidation boundary is always lower than. In addition, the results show the difference is larger with a higher risk aversion. Actually, the time inconsistent preference weakens the effects of risk aversion. That is, higher risk averse agent will delay the exit compared to the time consistent case. The entrepreneur would like to maintain the firm operation longer considering the existence of utility discount in future stage. Panel B indicates that the influences of correlation between the entrepreneurial business and public equity on the liquidation decision is ambiguous in both cases. measures the systematic risks involved in the firm operation, and thus increasing brings more systematic risks which encourages the agent exit sooner. On the other hand, correlation between the firm and the public equity offers a way for the entrepreneur to hedge the risks and thus delay the liquidation. Panel B shows the non monotonic result and we find that the hedge effect is a little more

significant in time inconsistent case. Therefore, is always lower than.

The magnitude of utility discounting parameter and Poisson process intensity determine the degree of the entrepreneurial time inconsistency. Figure 2 presents the effects of and in our model. Panel A plots the CE wealth in complete-market when (i.e.) at various levels of. decrease sharply when is around 0. With increasing, turns to be stable and approaches the future state (case) steady result. Panel B plots the liquidation boundary at different. The setting of inconsistent preferences requires the entrepreneur to maintain the firm operation longer as to offset the utility discount in future stage while panel B indicates that the liquidation decision is non monotonic with. When the agent’s preference just changes to inconsistency from consistent setting (near), the desire to maintain the firm operation dominates and the liquidation boundary decreases with. But the typical entrepreneurial dynamics turns to dominate and the exit choice approaches the future stage steady result in a higher level of. Panel C and D plot the influences of utility discount on and. Decreasing leads to a lower and delays the liquidation. Panel D indicates that the agent lacks sensitivity to when the discount factor is close to 1 and the liquidation boundary is reduced sharply at a lower level of.

4.2. CE Wealth and Investment Decision

The time inconsistency affects not only the liquidation choice but also the wealth and operation strategies. Figure 3 plots the effects of inconsistency on CE wealth, Tobin’s q, entrepreneurial investment and con- sumption. We define private enterprise value for the firm as follows:. The entrepreneurial average q is given by the ratio between private enterprise value and capital:

. Panel A and B show that the CE wealth and average q is significantly lower in

time inconsistent case. Panel C plots the investment decision and indicates that there exist both over- and under- investment in time inconsistent case compared to the constant preference. The entrepreneur will invest less when his liquid wealth approaches the liquidation threshold. In a higher level of liquid wealth, on the other hand, the inconsistent preference agent will invest more than standard model. Panel D presents the consumption in two preference settings. The inconsistent agent will consume less and this reflects their precautionary saving con- sidering the utility discount in the future stage.

Figure 4 plots the effects of and on the entrepreneurial wealth and investment decisions when the

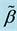
agent’s liquid wealth equals the capital. CE wealth decreases sharply when is close to 0. With increasing, turns to be stable and approaches the future stage value (case). Panel B shows that the investment decision is non monotonic with. As we have stated above, the inconsistent preference encourages the entrepreneur maintain the firm operation longer. In the investment decision process, it is intuitive that the inconsistent agent would invest more than consistent case as a compensation for the utility discount in future stage. On the other hand, higher means it would be more possible for the birth of the future stage. Therefore the entrepreneur will invest less and make more precautionary saving. Panel B exhibits this ambiguous effects. At a low level of, the entrepreneur will invest more to offset the utility discount in the future stage. With increasing, the precautionary saving starts to dominate and the investment turns to approach the lower future stage investment strategy. Panel C and D plot the CE wealth and investment at various. captures the degree of the utility discount in the future stage and thus it is intuitive that the CE wealth will be reduced when. Panel C shows that decrease sharply when reducing. Panel D indicates that investment is higher than the consistent case and our result presents the negative correlation between and exists all the time with inconsistency setting. With decreasing, the precautionary saving become meaningless given the huge utility discount in future compared to present age and thus the agent would like to invest more in the firm operation to obtain risky but high return in contemporary stage.

5. Conclutions

This paper extends the entrepreneurial dynamics model to account for time inconsistent preferences. Entrepreneurs need to formulate the investment decisions taking into account the possibility of future stage with utility discount. This sets up a conflict between two opposing forces. First, the agent desires to take advantage of the option to exit, and also has an incentive to invest more and longer to offset the utility discount in future stage. Second, the time inconsistent preference lead to motivation of precautionary saving and thus reducing the investment. We extend the model of [2] to consider the decision making process for an industry made up of time inconsistent entrepreneurs.

We find that time inconsistency leads to under investment when the entrepreneurial liquid wealth is close to the liquidation boundary and over investment when the liquid wealth is far away from the exit threshold. For further analysis, we study the effects of some key factors in our model. Inconsistency weakens the effects of risk aversion which accelerates the liquidation. The effects of the correlation between the firm and the public equity are ambiguous and non monotonic in both cases, but the inconsistent setting delays the exit decision compared to consistent model. The magnitude of Poisson process intensity and the utility discount determine the degree of the entrepreneurial time inconsistency. Increasing promotes the possibility for the birth of the future stage in which there exists utility discount. We find that the entrepreneurial CE wealth is negatively correlated with and will approach the future stage steady value with increasing. The effects of on the liquidation decisions and the investment strategy are ambiguous. At a low level, increasing delays the liquidation and promotes the investment. But a higher accelerates the exit and reduces the investment. measures the utility discount in future stage and thus the entrepreneurial CE wealth decreases sharply when reducing. The investment is negatively correlated to. The liquidation boundary becomes stable when is close to 1 but decreases significantly when is lower.

Acknowledgements

Jinqiang Yang acknowledges support by Natural Science Foundation of China (#71202007 #71472117), New Century Excellent Talents in University (#NCET-13-0895) and Chen Guang Project of Shanghai Municipal Education Commission and Shanghai Education Development Foundation (#12CG44).

References