Received 30 July 2014; revised 13 September 2014; accepted 28 September 2014

ABSTRACT

This research paper is focused on the modelling of credit rating, using reduced form approach, in which intensity is defined endogenously based on the firm’s cashflow. It was modelled with reflected stochastic differential equation; this was adopted to evaluate the credit rating of a firm where the reflection function 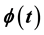(i.e. Brownian local time) was used to detect default and measure time spent at default. Through this, the credit rating is estimated within [0,1]; where “0” is the state of default and “1” is interpreted as undefaultable within a time interval 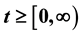under consideration.

Keywords:

Brownian Local Time, Credit Rating, Cashflow, Default, Reflected Stochastic Differential Equation, Undefaultable

1. Introduction

The mathematical modelling of stock market using Brownian motion according to Protter [1] and Hobson [2] was first introduced in 1900 by L. Bachelier in his Ph.D thesis where he modelled the flunctuation of assets prices and the price derivatives. Protter in [1] claimed that Bachelier’s work was not recognised but was re- discovered by L. Savage in the 1950s. He later alerted P. Samuelson [3] who suggested the use of geometric Brownian motion to model stock prices.

A major breakthrough occurred in 1973 when Black and Scholes [4] proposed a method to price European options via an explicit formula by making use of Itŏ stochastic calculus and the Markov property for diffusion. In the same year, Merton [5] with some modifications showed that the same analysis could be applied to American options on non-dividend paying common stocks. In the last two decades, the idea of using stochastic calculus for modelling prices of risky assets has generally been accepted and this has interestingly led to a new branch of applied probability theory called Mathematical Finance.

One of the most recent research areas in mathematical finance is the modeling of credit risk. Until recently, obligors were either classified to be of “good credit” and assumed not to default in payment of debt, or said to be of “bad credit” and failure to fulfill financial obligation was assumed. Probability of default was only introduced in the 1990s and financial institutions such as banks started to manage their credit portfolio using credit ratings.

M. Jeanblanc in [6] had earlier modelled default risk by providing a detailed analysis of a case when the flow of information available to an agent reduced to the observations of the random time which modelled the default event. In the research work, a restricted condition was posed in the model by assuming an hypothesis which postulated the invariance of the martingale property with respect to the enlargement of the Brownian filtration by the observation of a default time. But in this paper, instead of such hypothesis, reflection of the boundary of a stochastic differential equation shall be used to model default.

The main focus of this paper is to model credit rating using one-dimensional reflected stochastic differential equation with motivation from A. V. Skorohod [7] , H. Tananka [8] , and N. Ikeda and S. Watanabe [9] [10] . This would be done through incomplete information model which was introduced by Duffie and Lando [11] and Giesecke [12] . It has been analysed by Giesecke [12] , Jarrow and Protter [13] amongst others that this model bridges the gap between the structural approach and the reduced form approach in modelling credit risk by the assumption of the completeness of information available to the modeler. This eventually makes a structural model whose default time is predictable to be transformed into a reduced form model whose default is totally a surprise. Based on this incomplete information about the firms asset or default barrier, the structural model becomes a reduced form model whose intensity of default is no more exogenously defined but now determined endogenously within the model.

2. Preliminaries

Definition 2.1. Let 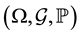be a probability space, a random variable is called a 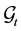- stopping time if 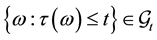for any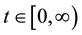. The stopping time 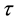is said to be predictable if there exists a non-decreasing sequence of stopping times 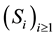with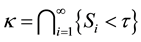, then

.

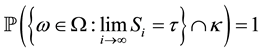The stopping time 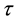is said to be totally inaccessible if it comes with no advance warning (i.e. a complete surprise). It can be defined as

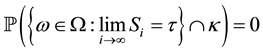
where 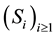is a non-decreasing sequence of stopping times as defined above.

Theorem 2.1. A uniformly integrable process 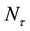such that 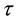is a finite stopping time is a submartingale if and only if it has a decomposition

where is a uniformly integrable martingale and is a predictable increasing process, both are null at 0.

Definition 2.2. A process is called the -compensator of the process if and only if the following conditions are satisfied:

i) is a -predictable increasing process, with.

ii) The process, called the compensated process, follows a -martingale.

Definition 2.3. Let be a one-dimensional Brownian motion defined on a probability space. A local time which can also be called a sojourn time density of is a non-negative random variable which satisfies the following properties:

i) is continuous.

ii) For every Borel subset of and

is unique and can be written as

.

A local time is a process that describe the amount of time a diffusion process has spent at a given point therefore providing a description of the sample path of the process.

Reflected Stochastic Differential Equations

We shall consider a one-dimensional diffusion process on which has only one boundary at. We define, where is the boundary of and is the interior of.

Let and be continuous, a one dimensional reflected stochastic differ- ential equation is as follows:

(2.1)

Remark 2.1. From [9] these equations can be intuitively interpreted as the following: The “reflection function” is a non-decreasing process whose point of increase is only when is on the boundary where it causes a reflection. It is called the local time of on. is defined as one-dimensional Brownian

motion in the ordinary time such that. The function describes the rate of sojourn of on the boundary. When then for the boundary is said to be non- sticky and this also called instantaneous reflection. When then. The boundary is

said to be sticky and this is also referred to as the delayed reflection.

Definition 2.4. Let be a probability space with a filtration. We call a family of stochastic process a solution of (2.1) if the following holds:

i) is a -valued continuous -adapted process.

ii) is a continuous -adapted increasing process such that and

for a.s.

iii) There exists a one-dimensional Brownian motion with a.s.

iv) With probability one,

.

Theorem 2.2. Let and be measurable functions that

satisfy the linear growth and Lipschitz condition and let be a continuous non-decreasing process, having point of increase only at the zeros of, then there exist a unique -valued solution for the reflected stochastic differential equation

.

Proof. See [8] and [10] .

3. Main Result

Let be defined as a filtered complete probability space where is the information set available to the manager of the firm to be rated. If is the net value of the firm at time, then

.

Let another filtration be defined which contains a reduced information set such as cash flow of the firm. This implies that. The default time of the model with the filtration becomes totally inaccessible stopping times because the information set has been reduced from the one being constantly monitored by the manager with predictable default time. Hence, it is a reduced form model with endogenously defined intensity on the firm’s economic fundamentals which is cashflow.

Let us consider a one-dimensional reflected stochastic differential equation which shall be used to model credit rating of a firm. The model will assess the firm based on the cash flow over a period of time, it will show the credit rating of such firm between the interval [0,1] where point “0” means the firm is at a state of default which is the lowest rating and the point “1” means the firm is undefaultable which is the highest rating. The relevant barrier to be considered in this model is, where negative cashflow is still assumed to be at point zero.

The model is made up of the following terms:

i) Let the cashflow of the firm. This is made up of cash inflow (i.e. bank loans, interest on savings etc.) and cash outflow (i.e. purchase of stock, purchase of raw materials etc.). is a markov process since the present cashflow of the firm over a period of time will be used to determine the future credit rating of the firm without any consideration of the past cashflow.

ii) riskless cash, which represents the cash inflow.

iii) risky cash, which represents the cash outflow.

iv) the reflection function that measures the time spent at default. It increases immediately the cashflow of the firm. Where we define and.

v) the default intensity.

vi) Let be defined as the rating of a firm at time. This a -martingale process since it is believed to be without any bias (i.e. it is “fair”).

vii) is default indicator process such that

viii) act as the compensator which describes the cumulative default intensity and it is

.

Since the default indicator process is a point process with one jump of size one at default, it is uniformly integrable, hence it is a submartigale. is an increasing predictable process since when therefore by Doob-Meyer decomposition (Theorem 2.1), the credit rating of the firm will be equal

.

Let us consider the following cases:

Case 1: Suppose throughout the period being considered, the cash inflow of the firm was always greater than the cash outflow (i.e. all through period), this implies that throughout the period the firm did not default. Hence, the credit rating of such firm is.

Interpretation: This means the firm is termed Undefaultable throughout the period considered and such firm can be recommended to investors for future investment with very low risk.

Case 2: When the cash inflow is less than the cash outflow during the period of time being considered, default occurs. Now, suppose the firm’s cashflow at time but there was a recovery from such default within a short period (i.e.), the default intensity is low. Hence the value of the cumulative

rate of default is also very small say. The rating of the firm in this is the case is

.

Interpretation: Hence, such a firm will have high credit rating and the closer it is to 1 the higher the rating. Therefore investors could consider such firm as low risk firm and if given a loan the interest rate will be small.

Case 3: Suppose on the contrary, when the cashflow, the firm tarried at this point for a very long period of time or equivalently if the cumulative time of default within the period is considerably large. The cumulative rate of default will be equally large say. Therefore, the rating of the firm in this case is.

Interpretation: Such firm will be rated very low. Therefore investors could consider such a firm as a high risk firm. Granting a loan to such a firm will require a very high interest rate.

Case 4: Finally, suppose the cashflow of the firm is through out all the period being considered, then such firm has a credit rating is.

Interpretation: Such firm is said to be at a default state and the firm is of very high credit risk. Investors are advised to avoid investing in such firm until a credit migration occurs when the firm moves from such a default state to at least with low credit rating.

4. Conclusions

In conclusion, a firm’s credit rating can be evaluated by investors in order to make decision on future invest- ments and this has been done by modelling credit rating with reflected stochastic differential equation where the reflecting function detects the default time and it measures how long the firm stays at the point of default. Case 1 and Case 2 can be suggested as the optimal solution for investor to minimise risk.

Further research can be done through multidimensional extensions by the use of systems of reflected stochastic differential equations to analyse a set of ratings for various indexes in the risk management of the relevant stochastic financial models.

Cite this paper

Adeyemi AdewaleSonubi, (2014) Credit Rating Modelled with Reflected Stochastic Differential Equations. Journal of Mathematical Finance,04,333-337. doi: 10.4236/jmf.2014.45031

References