Received 18 May 2014; revised 23 June 2014; accepted 9 July 2014

Abstract

The main result of this paper is the construction of a strictly positive extension of any no-arbitrage price system defined on an incomplete market of any dimension and for any (finite) number of states of the world. This is proved by using the component functionals of the positive basis of the 2-dimensional lattice-subspace, which is spanned by the riskless asset and any of the state-dis- criminating payoffs, which are generically existent in the span of the primitive, non-redundant assets of the incomplete market, whose time-period 1 payoffs are x₁, x₂,・・・, x_n, respectively. This result is also valid in the case where the market is complete. Both of these results lead to a new statement of both of the Fundamental Theorems of Asset Pricing in the finite-state case.

Keywords:

Lattice-Subspace, Positive Projection, Positive Extension

1. Introduction

The First Fundamental Theorem of Asset Pricing states that the absence of arbitrage for a stochastic process X is equivalent to the existence of an equivalent martingale measure for X. The Second Fundamental Theorem of Asset Pricing states that the completeness of the market is equivalent to the uniqueness of this equivalent martingale measure. In the case of finite markets, this is the famous Harrison-Pliska Theorem, proved in [1] , mainly using the notion of stopping time. This theorem is related to the viability of a market model developed extensively in [2] , about the relation between viability and existence of equivalent martingale measures, see [3] . These results are generalized in [4] , under the same general frame of investors’ preferences, while they require certain integrability conditions for the price process. However, the least restrictive assumptions for the FTAP in finite markets are contained in [5] , where the origin of the ideas for its proof is the (non-) boundedness of the support of a probability measure in. A first Hilbert space proof of this Theorem was given in [6] . It was shown in [7] that for a locally bounded 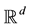-valued semi-martingale X the condition of No Free Lunch with Vanishing Risk is equivalent to the existence of an equivalent local martingale measure for the process X. It was proved in [8] that the local boundedness assumption on X may be dropped under the notion of equivalent 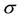-martingale measure. The work [2] , also discussed in [9] , is still essential in this topic and actually this work’s results rely on what Kreps established as viable market model consisted by an incomplete market and a linear price system on it. Recently, in [10] , a Fundamental Theorem of Asset Pricing and a Super-Replication Theorem in a model-independent framework are both proposed. However, these theorems are proved in the setting of finite, discrete time and a market consisting of a risky asset S, as well as options written on this risky asset. This work makes clear the relation between the span generated by options written on a risky asset and the Fundamental Theorems of Asset Pricing, which is exactly the topic of the present paper. The aim of this paper is to revisit the classical finite-state finance theory, in order to extract the Fundamental Theorems of Asset Pricing by using 2-dimensional lattice-subspaces. More specifically, a basis of such a lattice-subspace is consisted by the riskless asset and one of the famous state-discriminating payoffs, which were mentioned in the seminal article [11] . The point of the main result of this paper is that combining the prices of the call and put options on this portfolio in order to pick a price-system for all the states is not so simple. It definitely needs to know the span of the call and put options written on a market of primitive securities X, which is actually equal to the sublattice 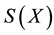generated by X, see [12] . This sublattice is generically equal to 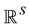in the sense of Lebesgue measure of 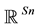and X also generically contains state-discriminating portfolios, under the same sense, too. This leads to the construction of a strictly positive extension of any no-arbitrage price system defined on an incomplete market of any dimension and for any (finite) number of states of the world. This is proved by using the component functionals of the positive basis of the 2-dimensional lattice-subspace, which is spanned by the riskless asset and any of the state-discriminating payoffs, which are generically existent in the span of the primitive, non-redundant assets of the incomplete market. These time-period 1 payoffs are denoted by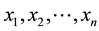, respectively. This result is also valid in the case where the market is complete. Both of these results lead to a new statement of both of the Fundamental Theorems of Asset Pricing in the finite-state case.

2. Preliminaries

2.1. Finite-Dimensional Ordered Linear Spaces

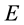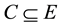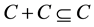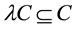Let be a Euclidean space. A set satisfying and for any 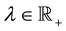is called wedge. A wedge for which 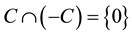is called cone. If ≥ is a binary relation on E satisfying the following properties:

1) 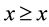for any 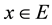(reflexive);

2) If and then, where (transitive);

3) If then for any and for any, where (compatible with the linear structure of E), then the pair is called partially ordered linear space. If

then this set is a cone of E and the binary relation is called component- wise partial ordering or usual partial ordering of. is a partially ordered linear space. The set is called (positive) wedge of the partial ordering ≥ of E. Given a wedge C in E, the binary relation defined as follows:

is a partial ordering on E, called partial ordering induced by C on E. If the partial ordering ≥ of the space E is antisymmetric, namely if and implies, where, then P is a cone. The usual partial ordering of is antisymmetric, its positive cone is and the partial ordering induced by on is actually the usual partial ordering. In the topological and the algebraic dual coincide. The partially or- dered vector space is a vector lattice under the usual partial ordering ≥, namely for any, both the supremum and the infimum of with respect to this partial ordering, exist in. If F is a sub- space of a vector lattice and the partial ordering induced on F by the cone makes F a vector lattice, then F is called lattice-subspace. Then for any, exist in F. Their relation to equivalent is the following:

If D is a subspace of having a basis, this basis is called positive basis if and only if

Choquet-Kendall Theorem [13] refers to the connection between finite-dimensional vector lattices and positive bases: A finite-dimensional ordered vector space E with a closed and generating cone is a vector lattice if and only if has a positive basis. Also in I.A. Polyrakis [13] , the determination of such a positive basis in the case of a finite-dimensional lattice-subspace of, where is some compact and Hausdorff topological space, is provided. Hence, Theorem [13] is also applicable on. A vector is a positive functional of a cone C in if and only if, while it is a strictly positive functional of C if and only if. If D is a subspace of and is a strictly positive functional of, or else a strictly positive functional of X with respect to the partial ordering induced by C on D, we say that is a strictly positive extension of g if and only if is a strictly positive functional of C and. A positive projection of being partially ordered by a cone C on the sub-space D being partially ordered by the cone is a projection, for which for any. A strictly positive projection is a positive projection which has the additional property:. As I.A. Polyrakis proved in [13] , the finite-dimensional lattice-subspaces in having positive bases with nodes, where is some compact and Hausdorff topological space, are examples of ranges of positive projections. Hence, Theorem [13] is also applicable on. The cone C is called generating if and only if. If C has interior points then C is generating for. Also, as a lattice

cone, is generating for. If E is partially ordered by C, then any set of the form

where is called order-interval of E. If E is partially ordered by C and for some, is called order-unit of E if and only if holds. If E is a normed linear space, then if every interior point of C is an order-unit of E. If E is moreover a Banach space and C is closed, then every order-unit of is an interior point of C. If, partially ordered by, then every, such that is an order unit. For more about ordered linear spaces, see [14] .

2.2. Finite-State Finance

Suppose that there are two periods of economic activity and S states of the world. At time-period there is uncertainty about the true state of the world, while at time-period this state is revealed. Suppose that there are n primitive assets in the market which are non-redundant, namely their payoff vectors at time period, are linearly independent. A portfolio in this market is a vector of in which denotes the units invested to the asset. If, then the investment to units of the asset denotes a long position on these units. If, then the investment to units of the asset denotes a short position on units of the asset. The payoff of a portfolio, if the payoff vectors are expressed in terms of the numeraire as well, is the vector. The range of the operator is called asset span of the market, derived by. In this article we suppose that, hence the market of is incomplete. A contingent claim is any liability, while a derivative is a contingent claim whose payoff is connected through a functional form to some portfolio payoff for the asset span of. If for some contingent claim there is some portfolio such that, then the contingent claim is called replicated or hedged (by the portfolio). Any portfolio such that is called replicating portfolio or hedging portfolio of. Classical examples of derivatives are (European) options, which include the corresponding call options and put options. Call and put options written on some asset under some risky strike vector. different from 1. If we denote such a vector by, In this case, the call option written on with strike price with respect to is the contingent claim whose payoff vector is. In the same way, the corresponding put option is. The last call option is denoted by, while the put option is denoted by. The call option and put option are called non-trivial if, respectively. This definition implies that for both of these vectors all of their components are positive and at least one of them is non-zero.

It is well-known that the completion by options of the asset span with respect to 1 is the vector subspace of which contains all the derivatives written on the elements of the asset span X, see [12] . It is also well-known (see [12] ) that the completion of X by options is the sublattice generated by.

Since is a sublattice and hence a lattice-subspace, it has a positive basis

This positive basis is a partition of the unit (see [12] ). Its elements are binary vectors, (see also [12] [15] ). The determination of this positive basis relies on [16] .

According to [12] , a vector is an -efficient fund if is the linear subspace of which is generated by the set of nontrivial call options and the set of non-trivial put options of.

We also remind of the statements of [12] , respectively:

Suppose that is a positive basis of, , and for each. Then the vector of is an -efficient fund if and only if for each.

Each non-efficient subspace of is a proper sublattice of.

Suppose that is a positive basis of and that with for each i. Then:

1) the nonempty set, where is the set of non-efficient subspaces of, is the set of -efficient funds of and the Lebesgue measure of is supported on;

2) is the subspace of generated by the set of the call options written on the elements of. If is the subspace of generated by the set of call options written on the elements of X.

Lemma 2.1. There exists an efficient fund with respect to the strike vector 1.

Proof. Direct from [12] .

We also have the following:

Proposition 2.2. If we suppose that the vectors of the date-1 payoffs of the primitive assets are linearly independent and, then, where, except a set of vectors

of Lebesgue measure zero in.

Proof. In the last part of [12] , we gave a brief proof about the fact that resolving markets have the property. It is also well-known that resolving matrices are in general position, namely the complement of the set of them is a null-set in the vector space of the matrices, whose entries are real numbers. Hence the super-set of all the -matrices (markets), such that where are linearly independent and they have the property that are also in general position.

If F is a subspace of a vector lattice E and the partial ordering induced on F by the cone makes a vector lattice, then is called lattice-subspace. Then for any,

exist in. Their relation to equivalent is the following:

in terms of the partial ordering of. About lattice-subspaces and their influence in economics see [12] [13] [16] [17] .

Theorem 2.3. The subspace created by a “generically existent” and the riskless asset 1 is a lattice-subspace of.

Proof. According to the Choquet-Kendall Theorem, see [13] Theorem, we have to prove that is closed and generating. is closed, since the component functionals of the basis are continuous. is generating, since is generating, becauce it contains the order unit 1, which is also an order unit for under the induced ordering implied by. Since is a closed subspace of it is also a complete space under the induced topology, hence by Baire Category the order unit 1 is also an interior point of, which implies that is generating.

Corollary 2.4. has a positive basis.

Proof. Direct from [13] , and 2.3.

3. Re-Statement of the Fundamental Theorems of Asset Pricing

Following standard definitions, (see in [17] ), an arbitrage-free price on the space X of marketed securities is a strictly positive functional on X. Namely, if f is such a price, it is a linear functional such that for any, where is the cone of the induced partial ordering of X (the positive cone of the ordering relation which is induced on X by the usual, component-wise partial ordering on). Since X is finite-dimensional and X is identified to the space of portfolios through, mentioned above, f may be defined through a portfolio price as follows:, where is a replicating portfolio of x.

Theorem 3.1. (1st FTAP) If for the incomplete market X, such that we may find a portfolio, which separates the states of the world, then every no-arbitrage price f of the market generated by is extended to a no-arbitrage price in the complete market. Moreover, if we suppose that the probabilities for the states of the world are given by the vector:

a vector of -continuous risk-neutral probabilities exists.

Proof. Since by Theorem 2.3. is a lattice-subspace, we may define the strictly positive projection

operator where is the normalized positive basis of L and

are the component functionals of it. The extension of f is. The relevant vector of risk-

neutral probabilities is exactly equal to. The relevant Radon-Nikodym derivative vector is

Theorem 3.2. (2nd FTAP) If the market X is complete and and also we may find a portfolio, which separates the states of the world, then the no-arbitrage price f in the market which is generated by is extended to a unique no-arbitrage price in the complete market. Moreover, if we suppose that the pro- babilities for the states of the world are given by the vector, the vector of risk-neutral probabilities is unique.

Proof. Appropriate linear combinations between the time-period 0 price of the portfolio e and the time-period 0 price of the riskless asset (set to be equal to 1), provide the prices of the marketed assets which denote the Arrow securities (since the market X is complete). These prices are the same for different state-dis- criminating portfolios, since otherwise arbitrage opportunities would exist. Moreover, there prices are positive for the same reason. Hence we may suppose that the unique price vector for the Arrow securities is given from. If this vector is normalized (divided by its -norm) then the unique risk-neutral

probability vector arises. The relevant Radon-Nikodym derivative vector is

4. Conclusion

This paper presents a proof of the First and the Second Fundamental Theorem of Asset Pricing in the two-date, finite-state model of financial markets. We first assume incomplete markets that contain the riskless asset. Our proof relies on the fact that for almost all of the incomplete markets the span of the call and the put options written on the payoffs of their asset span is equal to the complete market. Also, for almost all of these markets state-discriminating payoffs lying in the asset span exist. We prove that the span of each of these payoffs and the riskless asset is a lattice-subspace, which has a positive basis. By this positive basis we construct any of the equivalent martingale measures―even the unique one in the case of the complete markets. Hence we obtain the proof by the geometric properties of the asset span, and moreover in the sense of arbitrarily small perturbations which do not alter the results.

References

[1] Harrison, M.J. and Pliska, S.R. (1981) Martingales and Stochastic Integrals in the Theory of Continuous Trading. Stochastic Processes and Their Applications, 11, 215-260. http://dx.doi.org/10.1016/0304-4149(81)90026-0

[2] Kreps, D.M. (1981) Arbitrage and Equilibrium in Economies with Infinitely Many Commodities, Journal of Mathematical Economics, 8, 15-35. http://dx.doi.org/10.1016/0304-4068(81)90010-0

[3] Harrison, M.J. and Kreps, D.M. (1979) Martingales and Arbitrage in Multiperiod Securities Markets. Journal of Economic Theory, 20, 381-408. http://dx.doi.org/10.1016/0022-0531(79)90043-7

[4] Duffie, D. and Huang, C. (1986) Multiperiod Security Markets with Differential Information. Journal of Mathematical Economics, 15, 283-303. http://dx.doi.org/10.1016/0304-4068(86)90017-0

[5] Dalang, R.C., Morton, A. and Willinger, W. (1990) Equivalent Martingale Measures and No-Arbitrage in Stochastic Securities Market Models. Stochastics and Stochastic Reports, 29, 185-201. http://dx.doi.org/10.1080/17442509008833613

[6] Schachermayer, W. (1992) A Hilbert Space Proof of the Fundamental Theorem of Asset Pricing in Finite Discrete Time. Insurance: Mathematics and Economics, 11, 249-257. http://dx.doi.org/10.1016/0167-6687(92)90013-2

[7] Delbaen, F. and Schachermayer, W. (1994) A General Version of the Fundamental Theorem of Asset Pricing. Mathematische Annalen, 300, 463-520. http://dx.doi.org/10.1007/BF01450498

[8] Delbaen, F. and Schachermayer, W. (1998) The Fundamental Theorem of Asset Pricing for Unbounded Stochastic Processes. Mathematische Annalen, 312, 215-250. http://dx.doi.org/10.1007/s002080050220

[9] Schachermayer, W. (2002) No Arbitrage: On the Work of David Kreps. Positivity, 6, 359-368. http://dx.doi.org/10.1023/A:1020262419556

[10] Acciaio, B., Beiglböck, M., Penkner, F. and Schachermayer, W. (To Appear) A Model-Free Version of the Fundamental Theorem of Asset Pricing and the Super-Replication Theorem. Mathematical Finance.

[11] Ross, S.A. (1976) Options and Efficiency. The Quarterly Journal of Economics, 90, 75-89. http://dx.doi.org/10.2307/1886087

[12] Kountzakis, C. and Polyrakis, I.A. (2006) The Completion of Security Markets. Decisions in Economics and Finance 29, 1-21. http://dx.doi.org/10.1007/s10203-006-0059-z

[13] Polyrakis, I.A. (1996) Finite-Dimensional Lattice-Subspaces of and Curves of. Transactions of the American Mathematical Society, 348, 2793-2810. http://dx.doi.org/10.1090/S0002-9947-96-01639-X

[14] Jameson, G. (1970) Ordered Linear Spaces, Lecture Notes in Mathematics. Springer-Verlag, Burlin.

[15] Baptista, A.M. (2007) On the Non-Existence of Redundant Options. Economic Theory, 31, 205-212. http://dx.doi.org/10.1007/s00199-006-0095-5

[16] Polyrakis, I.A. (1999) Minimal Lattice-Subspaces. Transactions of the American Mathematical Society, 351, 4183- 4203. http://dx.doi.org/10.1090/S0002-9947-99-02384-3

[17] Aliprantis, C.D., Brown, D.J., Polyrakis, I.A. and Werner, J. (1998) Portfolio Dominance and Optimality in Infinite Security Markets. Journal of Mathematical Economics. 30, 347-366. http://dx.doi.org/10.1016/S0304-4068(97)00038-4

NOTES

^*This paper was written as a part of RIVAL Project-Supervisor: Professor Walter Schachermayer.