Journal of Mathematical Finance
Vol.04 No.03(2014), Article ID:45663,9 pages
10.4236/jmf.2014.43016
A Simple Generalisation of Kirk’s Approximation for Multi-Asset Spread Options by the Lie-Trotter Operator Splitting Method
Chi-Fai Lo
Institute of Theoretical Physics and Department of Physics, The Chinese University of Hong Kong, Hong Kong, China
Email: cflo@phy.cuhk.edu.hk
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 March 2014; revised 3 April 2014; accepted 21 April 2014
ABSTRACT
In this paper, by means of the Lie-Trotter operator splitting method, we have presented a new unified approach not only to rigorously derive Kirk’s approximation but also to obtain a generali- sation for multi-asset spread options in a straightforward manner. The derived price formula for the multi-asset spread option bears a great resemblance to Kirk’s approximation in the two-asset case. More importantly, our approach is able to provide a new perspective on Kirk’s approxima- tion and the generalization; that is, they are simply equivalent to the Lie-Trotter operator splitting approximation to the Black-Scholes equation.
Keywords:
Lognormalrandom Variables, Black-Scholes equation, Spread options, Kirk’s approximation, Lie-Trotter Operator Splitting method

1. Introduction
Spread options, whose payoff is contingent upon the price difference of two underlying assets form the simplest type of multi-asset options, are very popular in markets as diverse as interest rate markets, currency and foreign exchange markets, commodity markets, and energy markets nowadays [1] . Despite the rapid development of spread options, pricing spread options is a very challenging task and receives much attention in the literature. The major difficulty lies in the lack of knowledge about the distribution of the spread of two correlated
lognormal random variables. The simplest approach is to evaluate the expectation of the final payoff over the joint probability distribution of the two correlated lognormal underlyings by means of numerical integration. However, practitioners often prefer to use analytical approximations rather than numerical methods because of their computational ease. Among various analytical approximations, e.g. Carmona and Durrleman [1] , Deng et al. [2] , Bjerksund and Stensland [3] , Venkatramana and Alexander [4] , Kirk’s approximation seems to be the most widely used and is the current market standard, especially in the energy markets [5] . It is well known that Kirk’s approximation extends from Margrabe’s exchange option formula with no rigorous derivation [6] . Recently, Lo [7] applied the idea of WKB method to provide a derivation of Kirk’s approximation and discuss its validity. Nevertheless, it is not straightforward to provide a generalisation of Kirk’s approximation for the case of multi-asset spread option via this approach.
Accordingly, it is the aim of this paper to present a simple unified approach, namely the Lie-Trotter operator splitting method [8] , not only to rigorously derive Kirk’s approximation but also to obtain a generalisation for the case of multi-asset spread option in a straightforward manner. The derived price formula for the multi-asset spread option bears a great resemblance to Kirk’s approximation in the two-asset case. More importantly, the proposed approach is able to provide a new perspective on Kirk’s approximation and the generalisation; that is, they are simply equivalent to the Lie-Trotter operator splitting approximation to the Black-Scholes equation. Illustrative numerical examples for the three-asset spread options are also shown to demonstrate both the accuracy and efficiency of the extended Kirk approximation. Furthermore, it should be emphasized that our approach is completely different from the extended Kirk approximation proposed by Li et al. [9] . Li et al. suggested to approximate the sum of 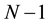 lognormal assets as a single lognormal variable and then apply Kirk’s approximation directly to this single lognormal variable and the remaining asset to price the
lognormal assets as a single lognormal variable and then apply Kirk’s approximation directly to this single lognormal variable and the remaining asset to price the 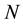 -asset spread option.
-asset spread option.
2. Two-asset Spread Options
The price of a European call spread option obeys the two-dimensional Black-Scholes equation
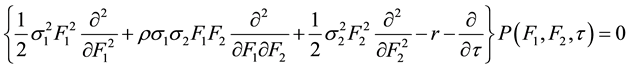 (1)
(1)
with the final payoff condition
 (2)
(2)
Here 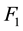 and
and 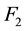 are the future prices of the two lognormal underlying assets,
are the future prices of the two lognormal underlying assets, 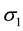 and
and 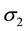 are the vola- tilities,
are the vola- tilities, 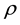 is the correlation between the two assets,
is the correlation between the two assets, 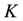 is the strike price,
is the strike price, 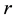 is the risk-free interest rate, and
is the risk-free interest rate, and 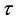 denotes the time-to-maturity. It is well known that no analytical solution is available in closed form and one needs to resort to numerical methods. In the following, we propose a simple derivation of the well-known price formula of Kirk’s approximation by means of the Lie-Trotter operator splitting method [8] .
denotes the time-to-maturity. It is well known that no analytical solution is available in closed form and one needs to resort to numerical methods. In the following, we propose a simple derivation of the well-known price formula of Kirk’s approximation by means of the Lie-Trotter operator splitting method [8] .
Proposition 1:
The price of the two-asset spread option can be approximated by
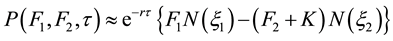 (3)
(3)
where
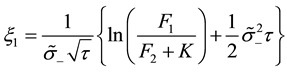 (4)
(4)
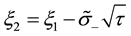 (5)
(5)
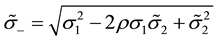 (6)
(6)

Proof:
In terms of the two new variables

Equation (1) can be rewritten as follows:

where


The final payoff condition now becomes

Accordingly, the formal solution of Equation (9) is given by

Since the exponential operator 

and obtain an approximation to the formal solution

for

It is not difficult to recognise that 

with the initial condition:

where 


As a result, we obtain

which is exactly the approximate price formula given in Equation (3). (Q.E.D.)
In terms of the spot asset prices, namely

where




It should be noted that for the Lie-Trotter operator splitting approximation to be valid, 





3. Multi-asset Spread Options
To price a European 


subject to the final payoff condition

where 








Proposition 2:
The price of the 

where






Proof:
Introducing the new variables: 



where




The formal solution of Equation (36) is given by

Then we apply the Lie-Trotter operator splitting method [10] to obtain an approximation to the formal solution

where the relation

is utilized.
Next, in terms of the two new variables

we rewrite 

where




It is clear that the exponential operator 
Lie-Trotter operator splitting method [10] again to approximate the operator by
result, we obtain

for

Since 



where


It is obvious that this approximate solution is identical to the approximate price formula given in Equation (29). (Q.E.D.)
In terms of the spot asset prices, namely

where





Obviously, this approximate price formula resembles the price formula of Kirk’s approximation in the two-asset case very closely. In fact, by setting 



4. Illustrative numerical examples for the Three-asset Spread Options
In this section, illustrative numerical examples are presented to demonstrate the accuracy of the extended Kirk approximation for the three-asset spread options. Although most spread options involve two assets only, yet there is a growing demand for three-asset spread options which can be found in the models for power plants or their financial equivalents―tolling contracts. We examine a simple three-asset spread option with the final payoff



















5. Conclusion
In this paper, we have proved that Kirk’s approximation for two-asset spread options can be rigorously derived
Table 1. Prices of a European three-asset call spread option. Other input parameters are: r = 0.05, s1 = s2 = s3 = 0.3, r12 = 0.4, r23 = 0.2, r13 = 0.8, S1 = 50, S2 = 60 and S3 = 150. Here “EK” refers to the extended Kirk approximation while “MC” denotes the Monte Carlo estimates with 900,000,000 replications. The relative errors of the “EK” option prices with respect to the “MC” estimates are also presented.
Table 2. Prices of a European three-asset call spread option. Other input parameters are: r = 0.05, s1 = s2 = s3 = 0.6, r12 = 0.4, r23 = 0.2, r13 = 0.8, S1 = 50, S2 = 60 and S3 = 150. Here “EK” refers to the extended Kirk approximation while “MC” denotes the Monte Carlo estimates with 900,000,000 replications. The relative errors of the “EK” option prices with respect to the “MC” estimates are also presented.
Table 3. Prices of a European three-asset call spread option. Other input parameters are: r = 0.05, s1 = 0.5, s2 = 0.4, s3 = 0.3, r12 = 0.4, r23 = 0.2, r13 = 0.8, S1 = 50, S2 = 60 and S3 = 150. Here “EK” refers to the extended Kirk approximation while “MC” denotes the Monte Carlo estimates with 900,000,000 replications. The relative errors of the “EK” option prices with respect to the “MC” estimates are also presented.
by applying the Lie-Trotter operator splitting approximation to the Black-Scholes equation, and that for cases with vanishing strike prices, the Lie-Trotter splitting approximation becomes exact and Margrabe’s formula is recovered. Our derivation also shows that Kirk’s approximation is more favourable for those cases with two positively correlated assets. Moreover, we apply the Lie-Trotter operator splitting method to obtain a genera- lisation of Kirk’s approximation for multi-asset spread options in a straightforward manner. The derived price formula for the multi-asset spread option closely resembles Kirk’s approximation in the two-asset case. By setting the total number of assets to be two, we can recover Kirk’s approximation readily. Thus, the ge- neralisation possesses the same nice features as Kirk’s approximation. For instance, as shown by the illustrative examples, the generalization is found to be very accurate and efficient in pricing the multi-asset spread options. All in all, our approach is able to provide a new perspective on Kirk’s approximation and the generalisation; that is, they are simply equivalent to the Lie-Trotter operator splitting approximation to the Black-Scholes equation.
References
- Carmona, R. and Durrleman, V. (2003) Pricing and Hedging Spread Options. SIAM Review, 45, 627-685. http://dx.doi.org/10.1137/S0036144503424798
- Deng, S.J., Li, M. and Zhou, J. (2008) Closed-Form Approximation for Spread Option Prices and Greeks. Journal of Derivatives, 15, 58-80. http://dx.doi.org/10.3905/jod.2008.702506
- Bjerksund, P. and Stensland, G. (2011) Closed Form Spread Option Valuation. Quantitative Finance, iFirst, 1-10.
- Venkatramana, A. and Alexander, C. (2011) Closed form Approximation for Spread Options. Applied Mathematical Finance, 18, 447-472. http://dx.doi.org/10.1080/1350486X.2011.567120
- Kirk, E. (1995) Correlation in the Energy Markets. Managing Energy Price Risk. Risk Publications and Enron, London, 71-78.
- Margrabe, W. (1978) The Value of an Option to Exchange One Asset for Another. Journal of Finance, 33, 177-186. http://dx.doi.org/10.1111/j.1540-6261.1978.tb03397.x
- Lo, C.F. (2013) A Simple Derivation of Kirk’s Approximation for Spread Options. Applied Mathematics Letters, 26, 904-907. http://dx.doi.org/10.1016/j.aml.2013.04.004
- Trotter, H.F. (1958) Approximation of Semi-Groups of Operators. Pacific Journal of Mathematics, 8, 887-919. http://dx.doi.org/10.2140/pjm.1958.8.887
- Li, M., Zhou, J. and Deng, S.J. (2010) Multi-Asset Spread Option Pricing and Hedging. Quantitative Finance, 10, 305-324. http://dx.doi.org/10.1080/14697680802626323
- Trotter, H.F. (1959) On the Product of Semi-Groups of Operators. Proceedings of the American Mathematical Society, 10, 545-551. http://dx.doi.org/10.1090/S0002-9939-1959-0108732-6
- Suzuki, M. (1985) Decomposition Formulas of Exponential Operators and Lie Exponentials with Some Applications to Quantum Mechanics and Statistical Physics. Journal of Mathematical Physics, 26, 601-612. http://dx.doi.org/10.1063/1.526596
- Drozdov, A.N. and Brey, J.J. (1998) Operator Expansions in Stochastic Dynamics. Physical Review E, 57, 1284-1289. http://dx.doi.org/10.1103/PhysRevE.57.1284
- Hatano, N. and Suzuki, M. (2005) Finding Exponential Product Formulas of Higher Orders. Lecture Notes in Physics, 679, 37-68.
- Blanes, S., Casas, F., Chartier, P. and Murua, A. (2013) Optimized Higher-Order Splitting Methods for Some Classes of Parabolic Equations. Mathematics of Computation, 82, 1559-1576. http://dx.doi.org/10.1090/S0025-5718-2012-02657-3
Appendix: Lie-Trotter Operator splitting method
Suppose that one needs to exponentiate an operator 
and


evaluate but 

exponential operator

operator splitting formula:

This can be seen as the approximation to the solution at 

composition of the exact solutions of the equations 


the Lie-Trotter splitting approximation can be found in Trotter [8] [10], Suzuki [11], Drozdov and Brey [12], Hatano and Suzuki [13], and Blanes et al. [14]. The Lie-Trotter splitting approximation is particularly useful for studying the short-time behaviour of the solutions of evolutionary partial differential equations of parabolic type because for this class of problems it is sensible to split the spatial differential operator into several parts each of which corresponds to a different physical contribution (e.g., reaction and diffusion).



