Journal of Mathematical Finance
Vol.3 No.3A(2013), Article ID:37588,19 pages DOI:10.4236/jmf.2013.33A004
Corporate Financing, Taxation, and Tobin’s q: Evidence from Japanese Firms and Industries
1Graduate School of Strategic Management, Chuo University, Tokyo, Japan
2Department of Economics, Sophia University, Tokyo, Japan
3Graduate School of Finance, Accounting, and Law, Waseda University, Tokyo, Japan
Email: kekubota@tamacc.chuo-u.ac.jp, susumu_3110@y2.dion.ne.jp, takehara@waseda.jp
Copyright © 2013 Keiichi Kubota et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received July 25, 2013; revised September 2, 2013; accepted September 18, 2013
Keywords: Tobin’s q; Corporate Tax Rate; Interest Tax Shields; RBC Model; Cost of Capital
ABSTRACT
This paper addresses the question of how taxation affects the cost of capital of firms and value of firms as measured by Tobin’s q. We construct a Real Business Cycle model and derive our original unlevered q on an after-tax basis, by removing financial tax shield effects in order to disentangle real operating profitability of firms and their financing decisions. Our model is an extended version of the two-sector general equilibrium model originally developed by Christiano and Fisher [1] and can incorporate both corporate and individual taxation. The unlevered q-value is derived from our general equilibrium solutions and some comparative static results are demonstrated with model predictions. In an empirical section of the paper, we find that the data support these model predictions, and thus they rationalize the use of our unlevered q. Our result possesses important policy implications for financial managers of the firms in correctly identifying firms’ true profitability aside from corporate tax shields as well as for the tax authority in changing the regulatory corporate tax rates.
1. Introduction
The question of how value of firms and their debt-equity ratios are determined is a focus of debates in corporate finance, macroeconomics [2], and microeconomics [3-5]. This issue is also closely related to the determination of the cost of capital on a before and after-tax base. Moreover, in public economics research, how taxation policies affect investment and financing decisions of firms [6,7] is the acute question, which needs to be investigated because the determination of the cost of capital after taxation directly affects investment behavior of firms as well as corresponding financing decisions.
In this paper, we extend a model developed in the macroeconomics literature to analyze this problem. The model is developed under homogenous expectations in the capital market and with labor immobility within the RBC model framework, which was originally developed by [1] in relation to Tobin’s q. [4] derived the q value under monopolistic competition, and [8] derived the q value with imbedded firms’ investment functions, but we incorporate the formulation of the corporate and personal tax in a general equilibrium model as was also used in [2].
Our paper is the first general equilibrium model which extends [1] with taxation parameters and the government sector, and it addresses our original concept of “unlevered q” within this general equilibrium framework1.
In the empirical part of the paper we focus on our constructed q variable because it is the variable that can highlight firms’ real productivity. With our model, we interpret estimation results for the cost of capital and our unlevered Tobin’s q on an after-tax basis using recent Japanese data, with particular attention to the different phases of business cycles.
As to the estimation method of our constructed Tobin’s q, even though the estimation of Tobin’s q in relation to firms’ investment decisions has been conducted by [11, 12] with estimated replacement cost for Japanese data, we utilize a simplified method proposed by [13,14] as advocated by [15]. The estimation method for the cost of capital in this paper follows that of [16], utilizing asset pricing theory in the finance literature. Our sample firms are non-financial firms listed on the First and Second Sections of the Tokyo Stock Exchange. The computations of the effective marginal tax rates are conducted utilizing a simulation method proposed by [17].
Section 2 demonstrates our two-sector RBC model and presents some comparative static results. Section 3 explains our data and the estimation method. Section 4 reports our empirical result. Section 5 reaches a conclusion.
2. Two-Sector General Equilibrium Model with Taxation and Government
The theoretical relationship between production technology and asset returns is previously analyzed in [18,19] in a general equilibrium model. The Euler condition equations where both investment returns and asset returns are included are derived by [20]. In this paper, we instead use a model developed by [1] to distinguish between firm decisions in the investment goods sector and consumption goods sector for which we expect business cycle implications to be quite different2.
In the current paper, we introduce a government sector as an extra agent to collect tax and conduct infrastructure investment, in addition to the two private sectors used in [1]. The government can change tax parameters, and accordingly, equilibrium values may change. We treat this government, however, as a passive agent and do not assume any kind of maximizing behavior on the part of government in our model for the sake of simplicity. In other words, our government just equates the tax income and its infrastructure investment as if it is an identity equation3. Our model is also closely related to [21] and [22], 2000) who analyze the business cycle differences between the investment goods sector and the consumption goods sector using a power utility function with habit persistence. [16] also introduces a financial sector as a straightforward extension of [21,22] and empirically analyze the business cycle co-movements of Japanese firms in the capital market.
In an original two-sector economy model by [1], consumption goods and investment goods are produced in separate sectors. Investment goods, which we call capital goods, are resold at the end of every period and depreciable, and consumption goods are perishable. The household commits her employment contract prior to realizations of the state of nature, and firms issue risk-free debt as well as equity. The household is assumed to be equipped with a log utility function with habit persistence. The original model of [1] is proven to follow the steady-state equilibrium path, and the equilibrium equity return, as a random variable, also follows the stochastic process for each production sector.
In this paper we extend their model by incorporating both the corporate tax and the individual income tax within their general equilibrium framework and also introduce the tax savings effect of utilizing firms’ debt, which is nothing but the subsidy by the government for the use of corporate debt. The question is whether that subsidy enhances a firm’s productivity or is detrimental to it. An answer to this question can be given by utilizing our new concept of the unlevered q.
Our model specification is the following. First, we write out the consumers’ problem. The preference for households is as shown in Equation (1). In Equation (1), Ct is consumption, 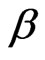 is a subjective discount factor
is a subjective discount factor , Xt is an evolution of habit stock whose movements are as described in Equation (2),
, Xt is an evolution of habit stock whose movements are as described in Equation (2), 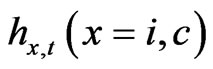 are the labor hours spent in the investment goods sector and in the consumption goods sector, respectively. The habit is the minimum level of desired consumption. Note the labor work hours are standardized to one as usual. Finally, the parameter
are the labor hours spent in the investment goods sector and in the consumption goods sector, respectively. The habit is the minimum level of desired consumption. Note the labor work hours are standardized to one as usual. Finally, the parameter  is a positive scalar to denote the utility derived from leisure4. As in [1] we assume that the there is pre-commitment in the household’s labor decision. Then, she decides her consumption decision as well as stock and bond holding decisions. However, as we explain below, we assume that firms announce their real investment decision and financing leverage decision plan just before the household reaches consumption and portfolio decisions. At the end of each period government collects tax and automatically invests in the infrastructure that determines the productivity technology level. Finally, the individual, firms, and the government simultaneously reach equilibrium for each. In other words, at the beginning of every period there are three staged discrete time frameworks as in a cash-inadvance model.
is a positive scalar to denote the utility derived from leisure4. As in [1] we assume that the there is pre-commitment in the household’s labor decision. Then, she decides her consumption decision as well as stock and bond holding decisions. However, as we explain below, we assume that firms announce their real investment decision and financing leverage decision plan just before the household reaches consumption and portfolio decisions. At the end of each period government collects tax and automatically invests in the infrastructure that determines the productivity technology level. Finally, the individual, firms, and the government simultaneously reach equilibrium for each. In other words, at the beginning of every period there are three staged discrete time frameworks as in a cash-inadvance model.
The expectations in (1) are taken at the end of the previous period 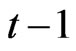 after the pre-committed working decision is
after the pre-committed working decision is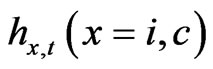 , already done as in cash-in-advance models.
, already done as in cash-in-advance models.
 (1)
(1)
where the habit evolves following (2),
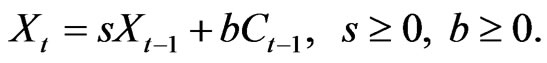 (2)
(2)
Then, the budget constraint for the household is the following. The portfolio decision is also made in conjunction with consumption decisions at the beginning of the period t but after the labor decisions are done. Note also it is done after the firm announces its investment and the leverage plan, the firm’s decision, and an individual’s decision is made simultaneously along with the government infrastructure investment.
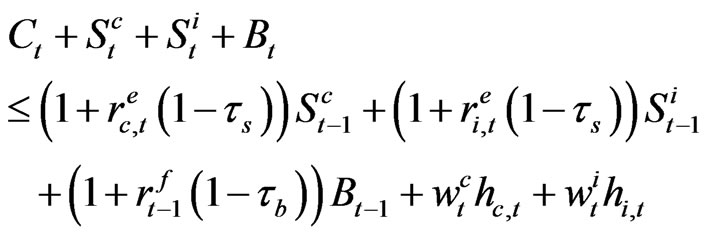 (3)
(3)
In Equation (3), 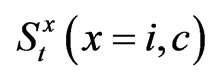 is the market value of equity at time t,
is the market value of equity at time t, 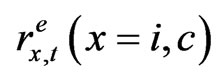 is the net rate of return on equity,
is the net rate of return on equity,  is the market value of corporate bonds,
is the market value of corporate bonds, 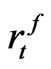 is the risk free bond rate, and
is the risk free bond rate, and 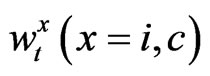 is the wage rate for each sector, Furthermore, we denote the average tax rate for the dividend and capital gains as
is the wage rate for each sector, Furthermore, we denote the average tax rate for the dividend and capital gains as , the tax rate for the interest income as
, the tax rate for the interest income as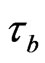 , and for future used corporate tax rate as
, and for future used corporate tax rate as 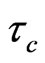 5. We abstract from ordinary income tax of the household from labor wages6.
5. We abstract from ordinary income tax of the household from labor wages6.
Then, the household’s first order condition with respect to the labor decision is the following (4), wherein  is the partial derivative of Equation (1) with respect to consumption where the expectation is taken with respect to time t+1 instead of t.
is the partial derivative of Equation (1) with respect to consumption where the expectation is taken with respect to time t+1 instead of t.
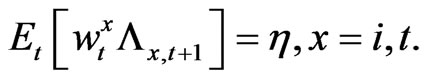 (4)
(4)
The optimum portfolio decision satisfies the following Euler conditions for stocks and bonds by solving for dynamic recursive Equation (1) assuming that the household also maximizes her/his consumption and investment decision from time 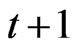 on after substituting (3) into (1) for
on after substituting (3) into (1) for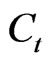 . By defining
. By defining 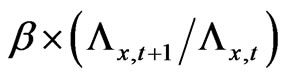 as
as 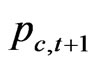 the relative price of consumption goods between time t and time
the relative price of consumption goods between time t and time  as an optimal solution for the consumer maximization problem, we get the following:
as an optimal solution for the consumer maximization problem, we get the following:
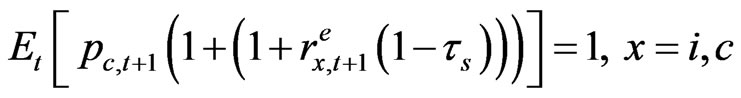 (5)
(5)
 (6)
(6)
The firms’ production decisions are as follows. There are two goods in an economy; i.e., perishable consumption goods and depreciable investment goods. First, the technology for producing consumption goods in period t is:
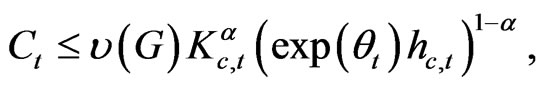 (7)
(7)
where Ct denotes consumption goods in period t, Kc,t denotes capital for producing consumption goods at the end of period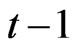 , and hc,t denotes the level of labor input in the consumption goods producing sector.
, and hc,t denotes the level of labor input in the consumption goods producing sector. 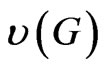 is the technology coefficient which is an increasing function of government infrastructure investment G. The covariancestationary technology shock θt is defined as in (8) where parameter ρ lies in the interval
is the technology coefficient which is an increasing function of government infrastructure investment G. The covariancestationary technology shock θt is defined as in (8) where parameter ρ lies in the interval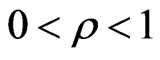 .
.
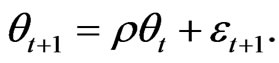 (8)
(8)
Here, random variable  is distributed as
is distributed as 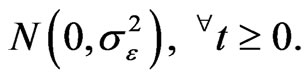 Second, the technology for producing new investment goods is:
Second, the technology for producing new investment goods is:
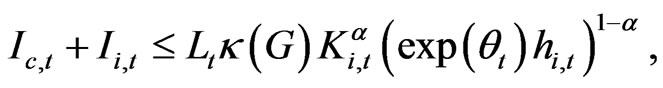 (9)
(9)
where 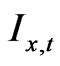 denote investment goods in sector
denote investment goods in sector , and hi,t denote employment in the investment goods producing sector7. In Equation (9),
, and hi,t denote employment in the investment goods producing sector7. In Equation (9), 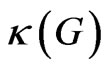 is the technology coefficient which is an increasing function of government infrastructure investment G. A logarithmic random walk technology shock Lt for this sector is defined as in (10)
is the technology coefficient which is an increasing function of government infrastructure investment G. A logarithmic random walk technology shock Lt for this sector is defined as in (10)
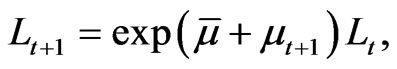 (10)
(10)
and 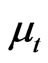 is distributed as
is distributed as 
Capital stock at the end of the period is governed by the following technology:
 (11)
(11)
where y denotes the previously installed capital and z denotes new investment goods. In Equation (11), 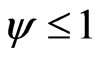 ,
, 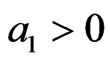 , and
, and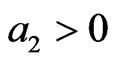 .
.
Next, we introduce the tax parameter g as defined in Equation (12). Let 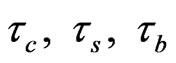 denote the corporate tax rate, personal average tax rate for holding stock, and personal tax rate on interest, respectively8. Then, by introducing the tax parameter g defined in Equation (12) below, we can obtain a constraint on firms’ financing decisions based on Miller’s formulation in [26]. We consider the economy before the Miller equilibrium is attained, in which the firm supply curve of the debt and the demand curve by the individual do not intersect9. This status is already verified for US firms by [27], in which he claims that the good firms do not take full advantage of government tax subsidy through the use of debt instruments because these firms want to keep their financial flexibility to prepare for financially bad times.
denote the corporate tax rate, personal average tax rate for holding stock, and personal tax rate on interest, respectively8. Then, by introducing the tax parameter g defined in Equation (12) below, we can obtain a constraint on firms’ financing decisions based on Miller’s formulation in [26]. We consider the economy before the Miller equilibrium is attained, in which the firm supply curve of the debt and the demand curve by the individual do not intersect9. This status is already verified for US firms by [27], in which he claims that the good firms do not take full advantage of government tax subsidy through the use of debt instruments because these firms want to keep their financial flexibility to prepare for financially bad times.
Thus, we define g here as
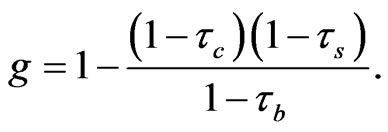 (12)
(12)
Since original stockholders receive tax shield benefits, the sum of investments on real assets and tax shields can be less than or equal to the total capital employed in the firm. The capital gains accrue to the original stockholders as an indirect subsidy from the government through a reduced corporate tax.
The firm’s financing constraint becomes the following inequality (13), where 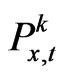 is the beginning period price of the old capital,
is the beginning period price of the old capital,  is the beginning period price of the new capital, Sx,t is the initial issue value of equity in industry x, and Bx,t is issued amount of risk-free debt and final term on the RHS side of the equation. The debt-tax shield accrues to the purchased stockholders and determines the next period return
is the beginning period price of the new capital, Sx,t is the initial issue value of equity in industry x, and Bx,t is issued amount of risk-free debt and final term on the RHS side of the equation. The debt-tax shield accrues to the purchased stockholders and determines the next period return 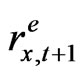 from holding the stock.
from holding the stock.
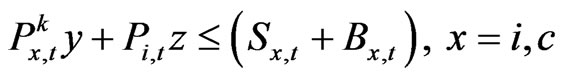 (13)
(13)
We also impose the condition that the firms set their own maximum debt amount by setting the firm target leverage ratio, partly due to flexibility reasons and partly to signaling reasons (see [16]). We denote this target leverage ratio as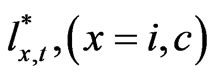 . This constraint is written in the following inequality (14). Because we assume that the firms have already announced the investment amount and the maximum leverage ratio at the second stage of the beginning of the period, this target will be specified by
. This constraint is written in the following inequality (14). Because we assume that the firms have already announced the investment amount and the maximum leverage ratio at the second stage of the beginning of the period, this target will be specified by 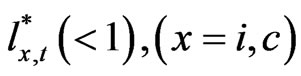 on the RHS of inequality (14).
on the RHS of inequality (14).
 (14)
(14)
Finally, as an objective function of the firms we assume that firms choose labor and capital to maximize the profit except after payment to the bondholders of both interest and principle and to the stockholders before tax gross return from holding stock as is the case in [1]10. Note the firm in [1] is resolved every period, and firms have to pay back both the principal and interest for its debt, pay the dividend, and also buy back the stock (or liquidation dividend) before the end of the period, which becomes 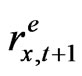 in the household budget constraint (3). The profit of the firm after the corporate tax and distributions to bondholders and stockholders but before the personal tax is as follows11:
in the household budget constraint (3). The profit of the firm after the corporate tax and distributions to bondholders and stockholders but before the personal tax is as follows11:
 (15)
(15)
Where 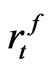 denotes a rate of return of risk-free debt and
denotes a rate of return of risk-free debt and  denotes a rate of return of an equity issued in period
denotes a rate of return of an equity issued in period  in sector x. In Equation (15) the economic depreciation rate of the capital is denoted as
in sector x. In Equation (15) the economic depreciation rate of the capital is denoted as  and
and 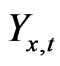 is the gross output of firms.
is the gross output of firms.
Then, the firm’s objective is to choose  to solve
to solve
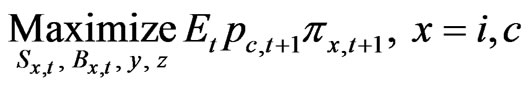 (16)
(16)
subject to constraints (13) and (14)12. The variable 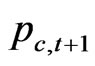 is the value, measured in date
is the value, measured in date 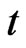 consumption units, of a unit of date
consumption units, of a unit of date  consumption goods indexed by state of nature and scaled by the conditional probability of that state of nature. This variable
consumption goods indexed by state of nature and scaled by the conditional probability of that state of nature. This variable 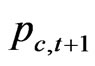 in (16) is defined as in the foregoing as the ratio of marginal consumption,
in (16) is defined as in the foregoing as the ratio of marginal consumption, 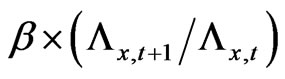 in the previous Equations (5) and (6). Then, firms maximize profit after the distribution to the stockholder and the bondholder before the personal tax.
in the previous Equations (5) and (6). Then, firms maximize profit after the distribution to the stockholder and the bondholder before the personal tax.
Let the marginal value to the firm of an extra unit of  be denoted by
be denoted by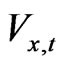 .
.
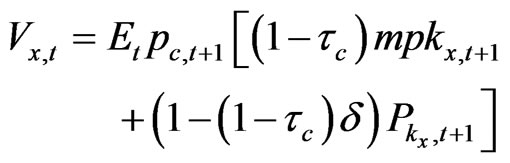 (17)
(17)
Where  denotes the marginal product of capital, denoted in period
denotes the marginal product of capital, denoted in period 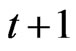 consumption units.
consumption units.
Let  be the Lagrange multiplier on the financing constraint (13) and
be the Lagrange multiplier on the financing constraint (13) and 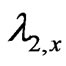 be the multiplier on the leverage target constraint (14). Then the Lagrange function to be maximized can be written as:
be the multiplier on the leverage target constraint (14). Then the Lagrange function to be maximized can be written as:
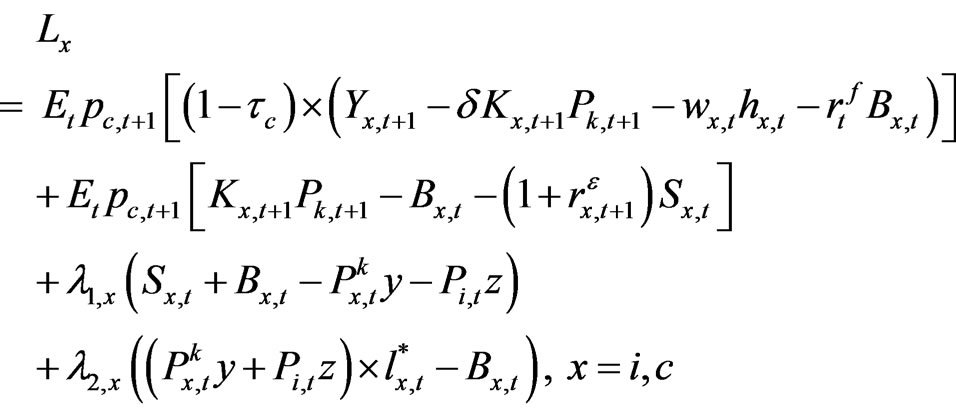 (18)
(18)
The first order optimality condition for (18) associated with 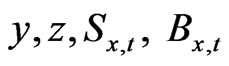 are respectively,
are respectively,
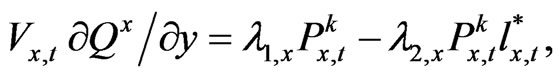 (19)
(19)
 (20)
(20)
 (21)
(21)
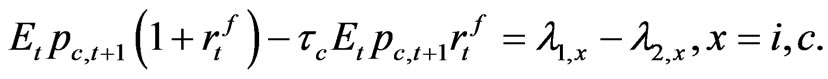 (22)
(22)
We can solve for these first order optimality conditions and the Euler conditions for households as well as for government revenue and the infrastructure identity Equation (28) in the following. Because the firm profit is zero and the government budget balances, it becomes the general equilibrium solution with the infinite lived household.
For this purpose let us first define the after tax bond return as  and
and 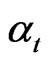 as
as
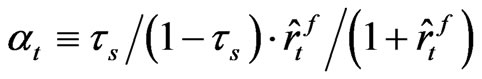 . By first solving for Lagrange multipliers, we get the following equation for the capital goods industry13. Note also that in this case the debt-equity ratio constraint is binding14.
. By first solving for Lagrange multipliers, we get the following equation for the capital goods industry13. Note also that in this case the debt-equity ratio constraint is binding14.
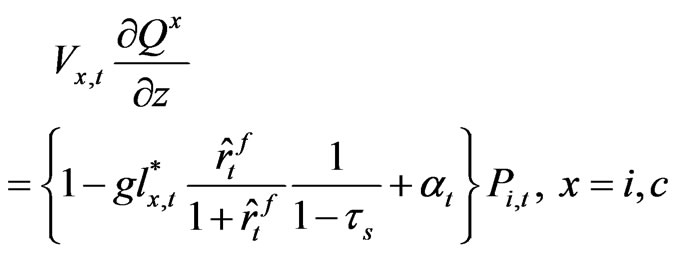 (23)
(23)
The LHS of the equation is a marginal value increase of the capital goods investment after tax for each sector, and the RHS is the price of the goods minus (inside the parenthesis) the government tax subsidy plus interest rate payments adjusted for interest rate tax.
Next, let us denote the firm value as 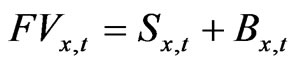 15. Since the relationship
15. Since the relationship
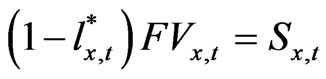 , we also get a following Equation
, we also get a following Equation
(24) as a value of the firm with debt.
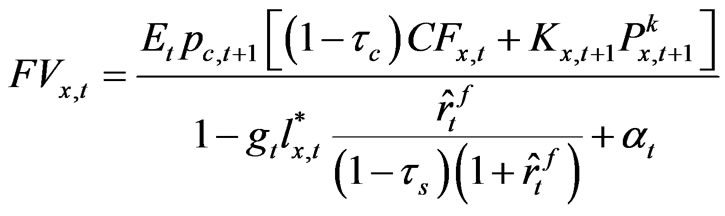 (24)
(24)
By denoting the first derivative of the 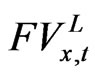 with respect to the productive capacity for the investment goods and the consumption goods as
with respect to the productive capacity for the investment goods and the consumption goods as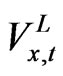 , we can derive the q ratio as the ratio of
, we can derive the q ratio as the ratio of 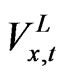 to
to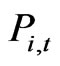 . It is because the optimization condition for q is that the marginal revenue after-tax of the investment has to be equal to the q ratio, while the marginal benefit of investment is
. It is because the optimization condition for q is that the marginal revenue after-tax of the investment has to be equal to the q ratio, while the marginal benefit of investment is 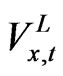 and the accompanying unit cost of investment is
and the accompanying unit cost of investment is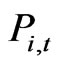 .
.
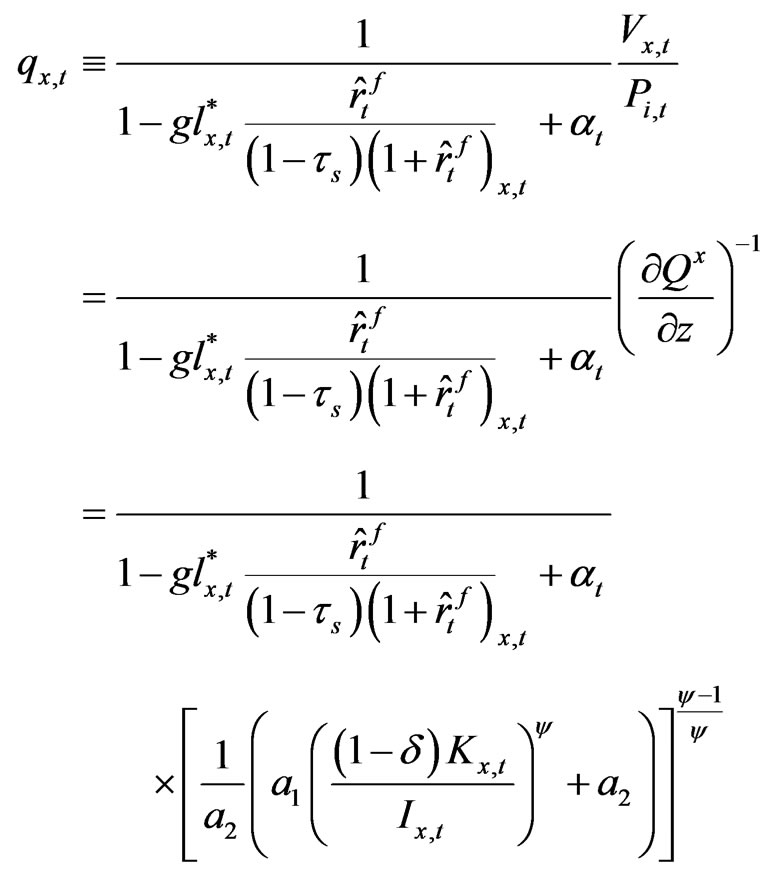 (25)
(25)
With this q value given, let us take a partial derivative of the q value with respect to the corporate tax rate and the debt ratio of the firm, respectively16.
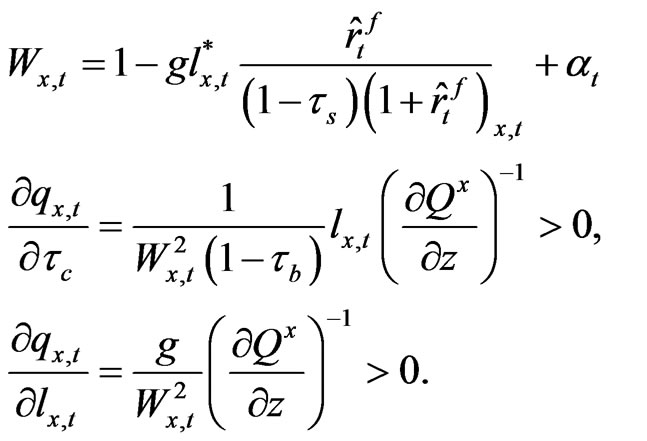 (26)
(26)
We find that our after-tax q is an increasing function of the corporate tax rate and debt ratio of the firm. The fact that q is an increasing function of the corporate tax rate may look counterintuitive because it means that raising the statutory corporate tax rate improves productivity of the firm. However, in Equation (25) note that the after-tax q-value is a product of two terms, one is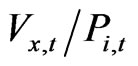 , and the other is,
, and the other is,
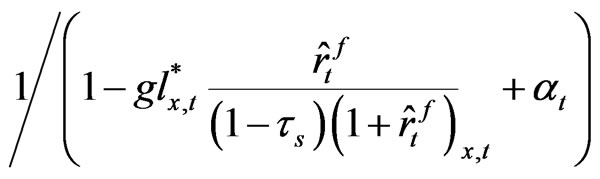 . The first term can be regarded as a q-value of an unlevered firm, and this construct, which we call “unlevered q-value”, is multiplied by the tax-shield factor
. The first term can be regarded as a q-value of an unlevered firm, and this construct, which we call “unlevered q-value”, is multiplied by the tax-shield factor
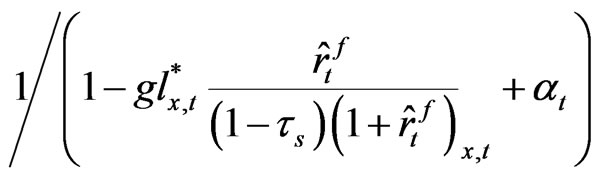 . Obviously, we observe that the conventional Tobin’s q is a decreasing function of the corporate tax rate, contrary to the case of our unlevered q. In this paper we compute both the ordinary q-values and unlevered q-values in the empirical part and we pay particular attention to the unlevered qvalues. It is because we believe that the unlevered qvalue is a more precise measure to identify a firm’s real productivity as well as the efficiency of capital allocations.
. Obviously, we observe that the conventional Tobin’s q is a decreasing function of the corporate tax rate, contrary to the case of our unlevered q. In this paper we compute both the ordinary q-values and unlevered q-values in the empirical part and we pay particular attention to the unlevered qvalues. It is because we believe that the unlevered qvalue is a more precise measure to identify a firm’s real productivity as well as the efficiency of capital allocations.
Note up to this point the firm is assumed to maximize ex ante profit every period and the derived equations above apply only for one period. When we extend our analysis into multi-periods with infinite horizon as steady state equilibrium, we can evaluate the tax savings as a present value of the perpetual stream. When we do this, the value of the perpetual tax benefits then reduces to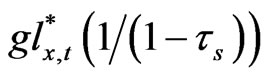 , and similarly the parameter
, and similarly the parameter 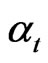 above reduces to
above reduces to 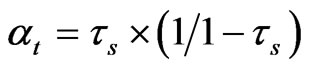 17,18.
17,18.
Thus, based on Equation (23) we get the following relationship.
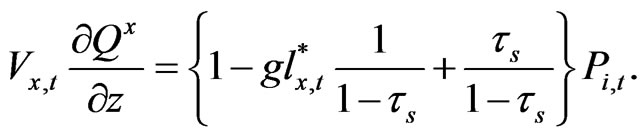 (27)
(27)
Finally, by simplifying (27) we get (28).
 (28)
(28)
This equation is the final equation that bridges the conventional levered q and our unlevered q, which we will estimate in Section 4 using time-series Japanese firm data by aggregating it into the investment goods sector and the consumption goods sector.
Before we end this section, we close our model by introducing the identity equation that equates the government infrastructure investment and the tax collections from corporate income and individual financial resources. However, note in the formulation of the model that we assumed that the corporation pays for these taxes in lieu of individuals a la McGrattan and Prescott (see [2]).
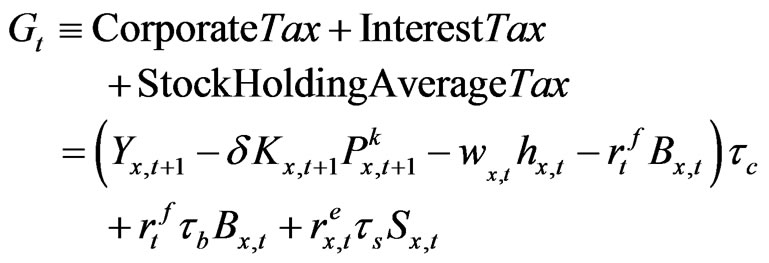 (29)
(29)
Note also that we assume  for governmental infrastructure investment.
for governmental infrastructure investment.
The equity rate of return formula for firms in the two production sectors in a tax-less world is given in [1,21] for a before-tax base. We extend this condition allowing for the corporate tax rate, stock holding tax rate, and the interest income withheld tax. Because the linear homogeneity of the firm’s objective, together with the inequality constraint (13), implies the equilibrium condition, 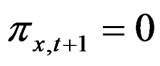 , for all
, for all  and for all states of the nature, we get
and for all states of the nature, we get
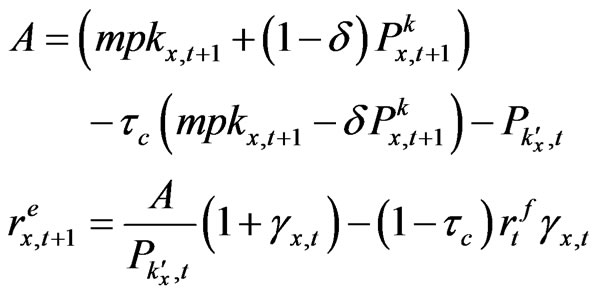 (30)
(30)
where 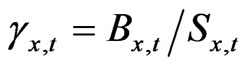 and
and 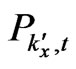 is the price of newly produced capital goods in sector i and sector c, for which the following (31) holds (see Appendix).
is the price of newly produced capital goods in sector i and sector c, for which the following (31) holds (see Appendix).
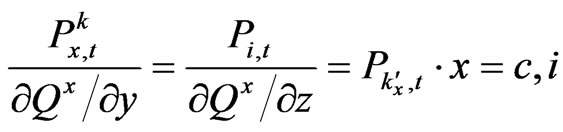 (31)
(31)
In (30) the excess return of both the investment goods sector and the consumption goods sector are functions of the capital stock and the debt-to-equity ratio of the corresponding sector, as well as various forms of tax rates. The consumption goods sector is also influenced by capital goods price changes and depreciation rates. The investment goods sector and the consumption goods sector are similarly influenced by the same capital goods price changes, while the marginal productivity of the two sectors, mpk, will be generally different among them.
These differences may cause different time patterns of the equity premium in two sectors along the different phases of the business cycles. Another parameter which produces different changes in equity premium between the two sectors is the leverage ratio of firms. Thus, the productivity parameter mpk, debt-to-equity ratio, tax rates, and the price of capital (market value of equity) all affect the rates of return on equity even before-tax as seen in Equation (30).
In Equation (30), the higher leverage causes the risk premium to be higher, as does the increase in the marginal productivity of labor and the future capital price. On one hand, higher personal taxation on capital income increases the before-tax required return. On the other hand, in our case, higher corporate tax and interest tax reduces the required rate of return19. In addition, faster economic depreciation will lead to lower required returns.
In the empirical section of the paper, we observe the time-series behavior of the required rate of return on equity and the unlevered q after-tax, and investigate how these values vary depending on historical changes in tax rates, the leverage ratios, and statutory tax rates as well as over the business cycles.
3. Data and the Estimation Method
Our data is all firms listed on the First and Second Sections of the Tokyo Stock Exchange between 1977 and 2007. The definition of each industry is from the Tokyo Stock Exchange 33 industry classifications. The definition of sectors we use is as follows. The consumption goods sector includes fisheries and agriculture, food, textiles and apparel, pharmaceuticals, electric appliances, and other products. The investment goods sector includes mining, construction, pulp and paper, chemicals, oil and coal products, rubber products, glass and ceramics products, iron and steel, nonferrous metals, metal products, machinery, transportation equipment, and precision instruments. The commerce sector includes communication, wholesale trade, retail trade, and services. The financial sector includes banks, securities, insurance, and other financial businesses. The transportation sector includes land, marine, and air transportation. Utilities include only power and gas. The real estate sector includes real estate and warehousing. The primary source for stock return data is the Nikkei Portfolio Master Data, and for financial variables we use the Nikkei NEEDS Data.
Our initial and conventional Tobin’s q estimates are computed using the simplified method proposed by [13, 14]20.
Our first Tobin’s q estimate for firm i in period t is defined as:
 , (32)
, (32)
where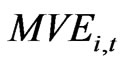 ,
, 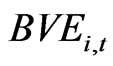 and
and 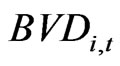 denote market value of equity, book value of equity and book value of debt of firm i in period t, respectively. On the other hand, based on Equation (14) we compute unlevered Tobin’s q estimates. The approximate unlevered q is:
denote market value of equity, book value of equity and book value of debt of firm i in period t, respectively. On the other hand, based on Equation (14) we compute unlevered Tobin’s q estimates. The approximate unlevered q is:
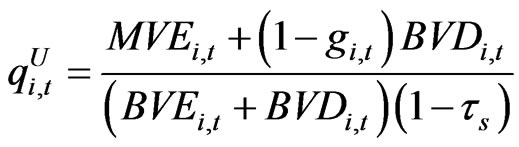 . (33)
. (33)
Note in the previous Equation (28) the after-tax Tobin’s q is equal to the product of unlevered q and the tax shield factor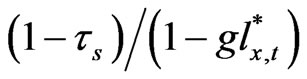 . The relation also holds between the approximate q defined in (32) and the approximate unlevered q defined in (33). One can easily check that the following (34) holds between the original Tobin’s q and our unlevered q from our stationary equilibrium solution for infinite horizons.
. The relation also holds between the approximate q defined in (32) and the approximate unlevered q defined in (33). One can easily check that the following (34) holds between the original Tobin’s q and our unlevered q from our stationary equilibrium solution for infinite horizons.
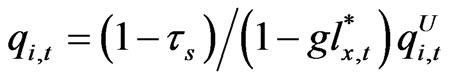 (34)
(34)
It is because the term 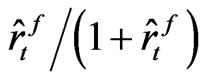 vanishes in equilibrium with infinite horizon time. Note that the numerator is discounted by
vanishes in equilibrium with infinite horizon time. Note that the numerator is discounted by 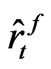 in this case for infinite cash flow stream and cancel out each other on the numerator and the denominator, and furthermore one period discount rate term of the denominator does not matter in the repeated stationary equilibrium after suitably adjusting for initial boundary values.
in this case for infinite cash flow stream and cancel out each other on the numerator and the denominator, and furthermore one period discount rate term of the denominator does not matter in the repeated stationary equilibrium after suitably adjusting for initial boundary values.
In computing the effective marginal tax rates for each firm and for each year we adopt the definition used by [32], which is: “the present value of the current plus deferred income taxes (both explicit plus implicit) to be paid par dollar of additional (or marginal) taxable income (where taxable income is grossed up to include implicit taxes paid)21.” We employ the simulation method proposed by [17] and estimate a simple time series model of taxable income for each firm. Thus, the two tax parameters in (33), 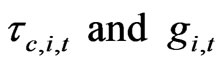 are different across all firms and also across all fiscal years.
are different across all firms and also across all fiscal years.
Here, the definition of income before-tax for our study is the sum of earnings before-tax as reported in financial statements and the net deferred tax balance divided by statutory tax rates in accordance with Japanese accounting standards22,23. The change in taxable income is defined as the change in earnings plus tax deferrals and it is assumed to follow the stochastic process (35), where 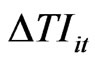 is the first difference of taxable income for firm i between the time period t and
is the first difference of taxable income for firm i between the time period t and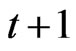 ,
, 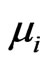 the mean drift parameter for firm i, and
the mean drift parameter for firm i, and 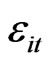 an identically and independent normal random variable for all t for each i with finite and constant variance.
an identically and independent normal random variable for all t for each i with finite and constant variance.
 (35)
(35)
The parameters of the taxable income process are estimated using the past five years of data both for the mean trend and the variance of the error term in (34) for each firm. Based on these parameter values, we then compute the expected present value of the increased tax when extra dollar (yen) income is earned by taking into account both the past five years of the tax loss carryforward benefits whenever applicable, as well as the future tax loss benefits in case firms incur losses for all 1,000 simulation paths in the future 20 years24. We use the 10 year JGB bond yield to discount the present value of tax benefits25. We also use future tax rates to compute the future tax readjustment amount by following current Japanese accounting standards26. With this method we compute the effective marginal tax rates for all firms.
4. Empirical Results
Table 1 reports the estimation results for the cost of equity for all firms listed on the First and Second Sections of the Tokyo Stock Exchange, using the version of conditional three-factor models as used in [37]. The observation period using the monthly stock return data is from September 1977 to June 2008. The detailed definition of the factor variables used is omitted, but a standard procedure is used for Fama and French three-factor model estimations, and it follows [16].
We estimate a conditional model, and for this purpose we use a natural logarithm of market size of equity and a natural logarithm of firms’ book-to-market ratio as instruments to let the sensitivity coefficient of the Fama and French three-factor model vary.
We estimate time series regression coefficients for individual stocks and take arithmetic averages for each industry as well as for two sectors used in our equilibrium model. The sector classifications are shown in the upper and lower rows of the table. We find that the cost of equity as measured in annual percent computed from the monthly data is slightly higher for the investment goods sector than for the consumption goods sector where the medians are 9.223% vs. 7.501%, and the means are 9.515% vs. 7.671%, respectively. The standard deviations are also larger for the investment goods sector with 9.795% vs. 7.671% and it implies the investment goods sector is riskier than the consumption goods sector. The size, measured by the natural logarithm of market value of equity in millions of yen, is similar between the two sectors with 10.438 vs. 10.476, and book-to-market ratios are higher for the investment goods sector at 0.725 than those for the consumption goods sector at 0.611, which means that the consumption goods sector is more of the “growth stocks” in Japan by usage in the financial economics field.
Table 2 shows summary statistics of the unlevered q which were computed using Equation (33) above. We find that the average value of the unlevered q is higher for the consumption goods sector at 1.507 than for the investment goods sector at 1.258. So is the case for the
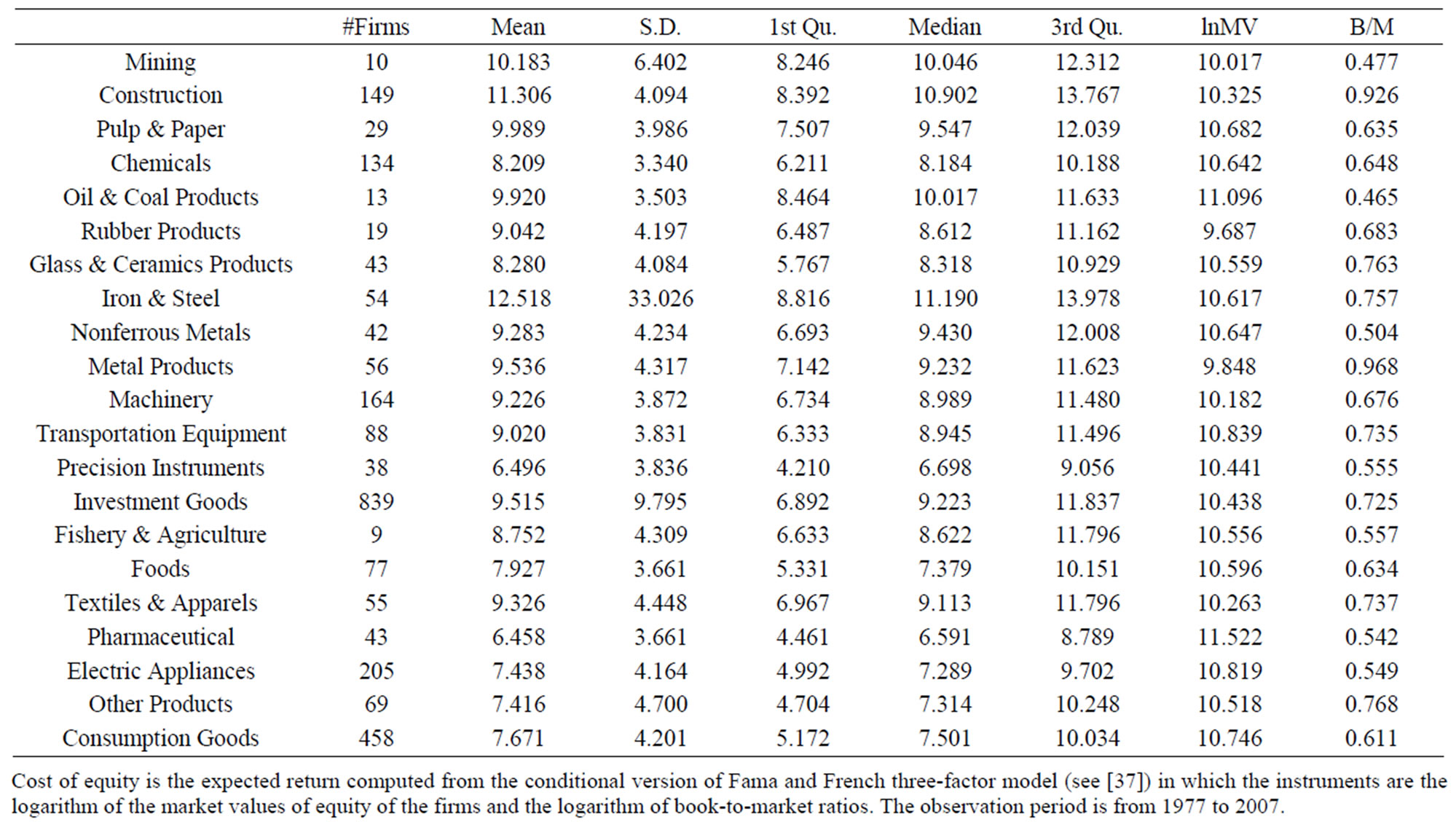
Table 1. Summary statistics of the estimated cost of equity.

Table 2. Summary statistics of unlevered Tobin’s q estimates.
median at 1.288 and 1.111, respectively. Because we are computing the unlevered q, it is not surprising that in some cases q values are smaller than one, which is what we expected from the definition of our unlevered q value as seen in Equation (33). Note also that similar results from a model with taxation in somewhat different contexts are presented in [8,38], in which the q-values can also become smaller than one in some selected cases. The finding that q-values can become below one after-tax is an important finding and also has important implications for both corporate taxation policies and individual taxation policies. The observation that all the numbers reported in the first quartile, except for the pharmaceutical industry, are less than one is a new finding of our paper. Finally, the median values are smaller than the means, implying the right skewness of our q-values.
Table 3 reports the effective marginal tax rates and debt-to-total-asset ratios for all firms based on a computing method as described in the previous section. The equity is measured in market value and the debt is measured in book value. When we compare the means and the medians, we do not find any difference in average values in effective marginal tax rates between the investment goods sector and the consumption goods sector with 0.372 vs. 0.373 and 0.408 vs. 0.408, respectively. Note the past effective statutory tax rates for large corporation groups in Japan varies between 0.4078 and 0.5498 during our sampling period, while the number, 0.408, which appears often for median values in Table 3, means that it is the marginal rate for relatively new firms facing the lower maximum statutory tax rate in recent years (See also Figure 1).
We find, however, that the debt-to-total-asset ratios are much higher for an investment goods industry which is required to have heavier equipment than a consumption goods industry. The means for an investment goods industry and a consumption goods industry are 0.545 vs. 0.422, and the medians are 0.552 vs. 0. 412. We further investigate how this difference in firms’ leverage ratios between the two sectors affects the behavior of our unlevered q values.
While all previous results reported are from pooled data, Tables 4 and 5 show the result where all stocks are reshuffled every year at the end of June; i.e., in Table 4 the criterion to sort is the effective marginal tax rate, and in Table 5 it is the debt-to-equity ratio27. After ranking stocks in each sector by the magnitudes of effective marginal tax rates and debt-to-total-asset ratios we report average values for the total period. From Tables 4 and 5, first of all we find that q ratios, both conventional and unlevered, are overall higher for the consumption goods sector than the investment goods sector28. We also find
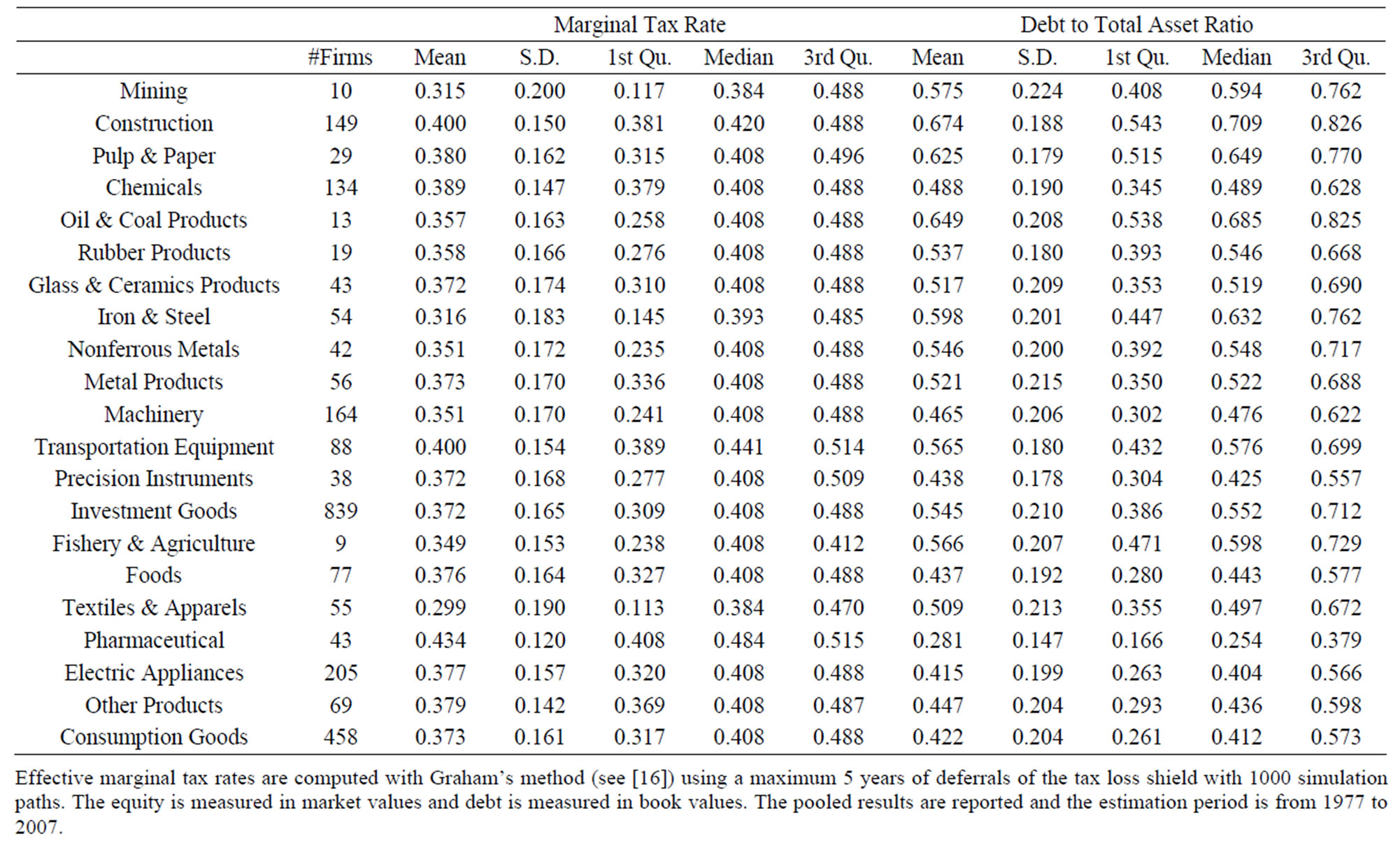
Table 3. Summary statistics of marginal tax rates and debt ratios.
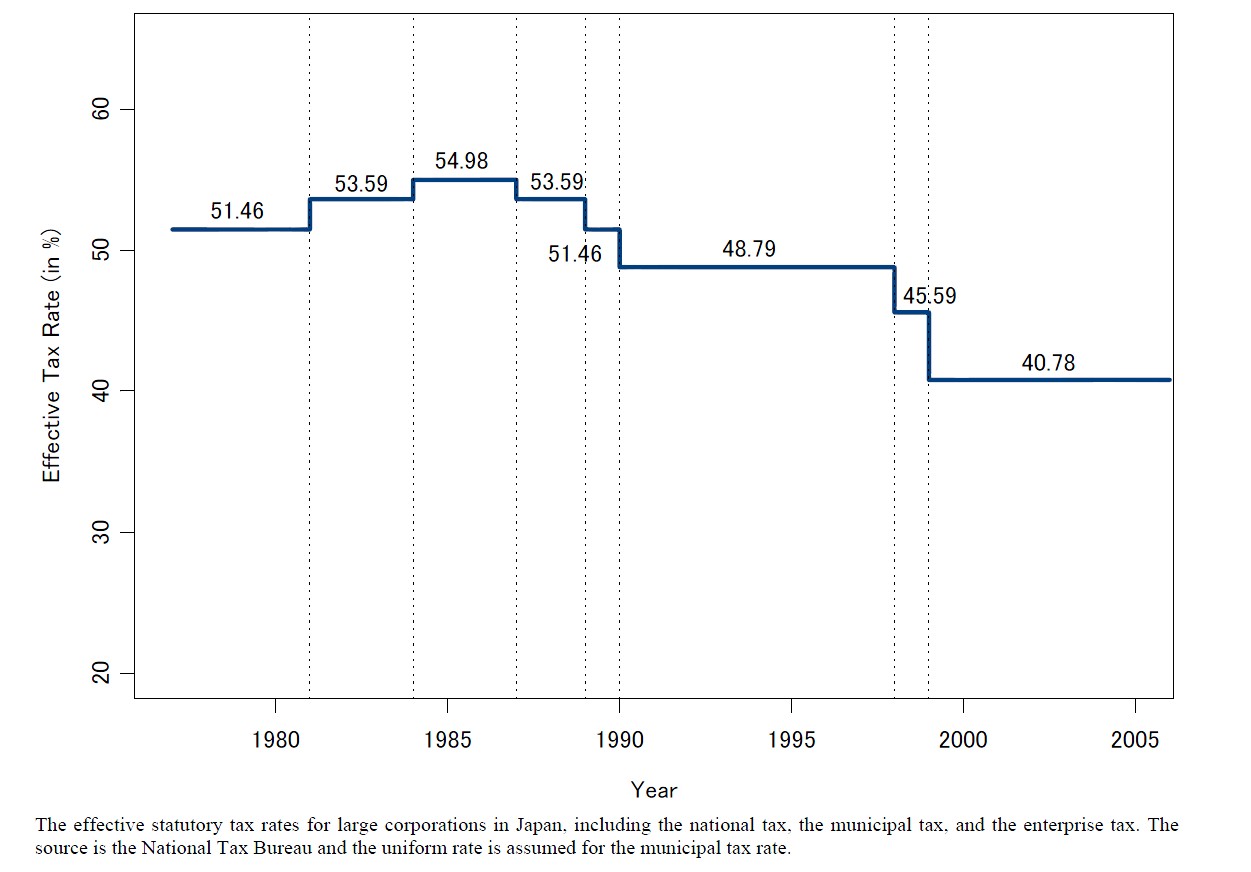
Figure 1. Trend of effective statutory corporate tax rates in Japan.

Table 4. Attributes of marginal corporate tax rate ranked portfolios.

Table 5. Attributes of marginal debt ratio ranked portfolios.
that the conventional Tobin’s q slightly overestimates the unlevered q, which purportedly shows the real productivity of firms apart from their financing decisions.
In Table 4, among the investment goods sector in Panel A, we find that firms with higher (lower) marginal tax rates tend to show a higher (lower) conventional Tobin’s q ratio, which means good firms are paying higher taxes. Firms with higher (lower) marginal tax rate brackets are the profit producing (losing) companies and thus show higher (lower) Tobin’s q. The tendency that the unlevered q increases as the tax rate increases, as predicted in the first inequality in (26), is supported except for the lowest tax paying group. The opposite tendency for the conventional q is not supported, but it may be due to the sample selection of good (bad) firms as the firms which signal (do not signal) that they are the good firms by paying higher tax rates [39]. The mere comparative static result may not be extended for this sorting scheme. Note the lowest tax group is the firms with the highest debt-to-equity ratios. When the marginal tax rates are the lowest at 0.130 and 0.144, with much tax loss carry forward benefits, it may be the case that the unlevered q where the individual capital gain tax rates 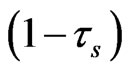 are included in the denominator may be pushing the unlevered q higher than the conventional q29.
are included in the denominator may be pushing the unlevered q higher than the conventional q29.
In Table 5 the firms with higher debt-to-equity ratios have lower Tobin q and the unlevered q. It is unfortunately inconsistent with the prediction from the second inequality of (26), but again we consider that is more due to the signaling behavior of the firms where the good firms do not borrow to the full extent to extract the tax benefits they can enjoy (Graham, 2000). We also find that the overestimation of the Tobin’s q is the largest among firms with the largest debt. In Panel A it is 12.17% (1.124 vs. 1.002) and it is 6.59% (1.246 vs. 1.169) in Panel B. So, we conclude that among firms with higher leverage ratios our method to correct for the overestimation of the conventional Tobin’s q is more important.
We also find that the cost of equity is higher (lower) for firms with lower (higher) marginal tax rate brackets in the case of the consumption goods sector in Table 4. It means the less (more) profitable, the higher (lower) the expected cost of equity. Also, in Table 5, the expected cost of equity in both sectors is higher (lower) for firms with more (less) debt. This is a reconfirmation of the old Proposition by Modigliani and Miller, but at the same time it validates the relationship of our Equation (30), in which we predict that our after-tax equilibrium required returns of equity in both sectors should be higher if the firms’ leverage ratios are higher. As for the realized returns as measured in monthly returns, we also observe that the tendency is similar to the case for the cost of equity.
Figures 2 shows the time-series pattern of the unlevered

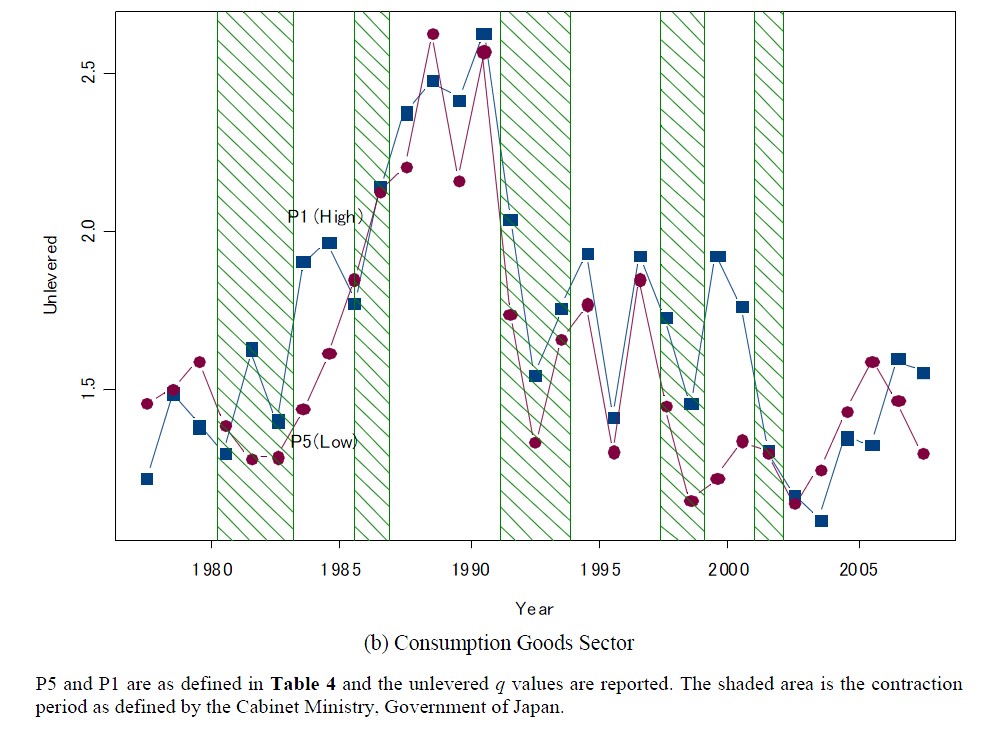
Figure 2. Time series pattern of unlevered q of marginal corporate tax rate ranked portfolios.
q-values for the highest ranked portfolio and the lowest ranked portfolio as ranked by effective marginal tax rates and Figures 3 shows the cumulative returns of these portfolios. Figures 4 and 5 show the same when ranked by debt-to-total-asset ratios.
In all the figures, the white part of the graph is the expansion period and the shaded part of the graph is the contraction period defined by the Cabinet Office, Government of Japan. In Figure 2 we find that firms with lower marginal tax rates show slightly but most of the time higher unlevered q values than firms with higher marginal tax rates for both sectors. Figure 3 demonstrates that firms with lower marginal tax rates attained higher realized returns than firms with higher marginal tax rates, as can be also confirmed from the utmost right column of Table 4.
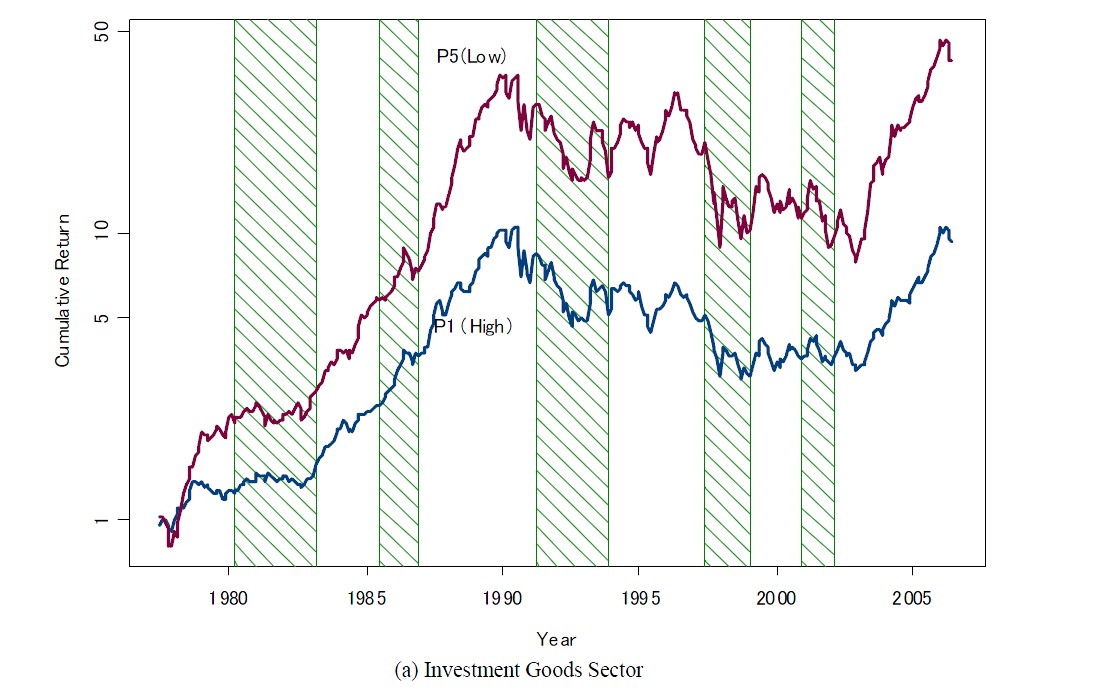
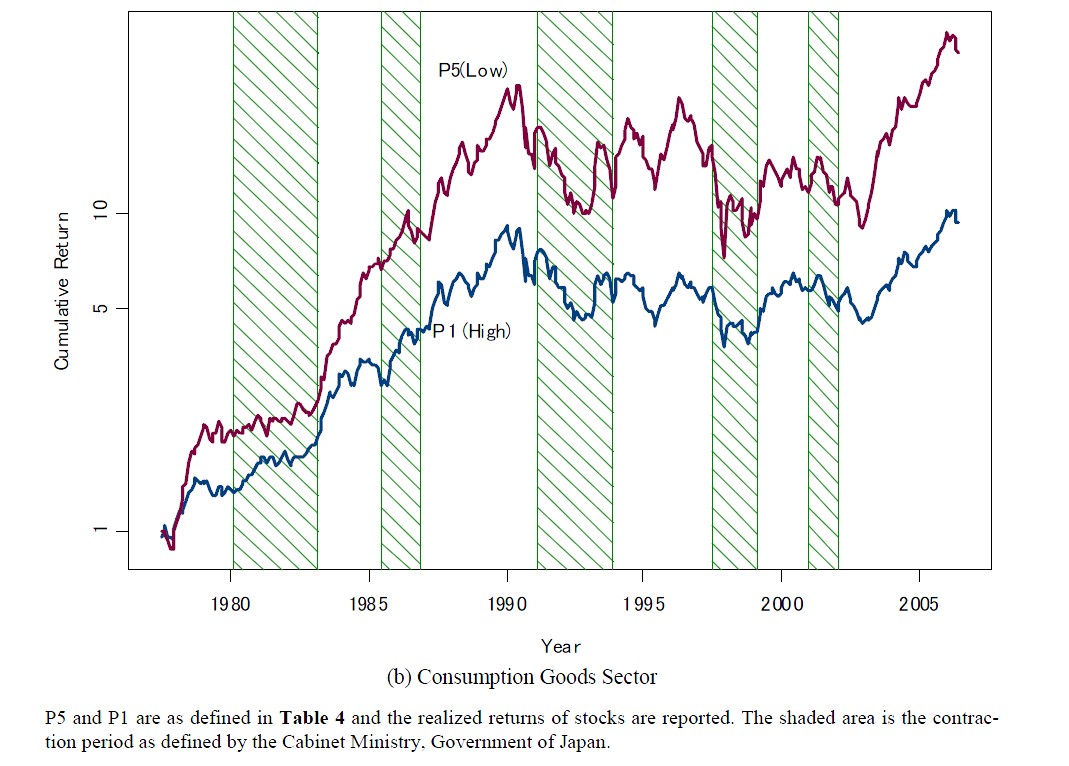
Figure 3. Cumulative returns of the marginal corporate tax rate ranked portfolios.


Figure 4. Time series pattern of unlevered q of debt ratio ranked portfolios.
In Figure 1 we indicate the decrease in corporate statutory tax rates in the years 1987, 1989, and 1990, and in the years 1997 and 1998 it has pushed up realized returns as can be seen from Figure 3. This observation is in accordance with the prediction from Equation (30) if we were to replace realized returns for expected returns for corporate tax rate changes. In recent years, the capital income tax rate has been also temporarily reduced from the statutory 20% to 10% in Japan until 2001, and that might have also helped push up realized returns in recent years, as can be observed from Figure 3.
The pattern of the results is similar for Figures 2 and 4,

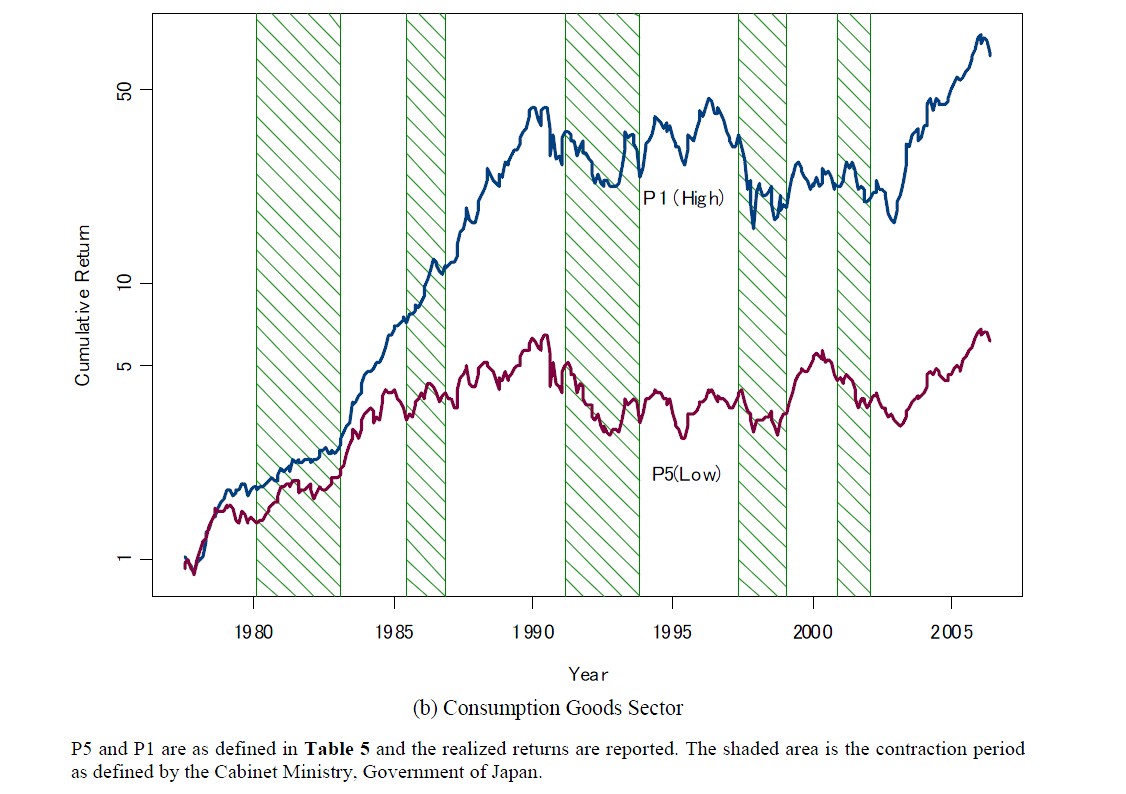
Figure 5. Cumulative returns of the debt ratio ranked portfolios.
while the variable for ranking is different. The differentiating power of the debt-to-equity ratio variable seems stronger as these figures show, and, unlike the case for marginal tax rates, the difference between the two portfolios becomes much wider during the bubble period of Japan in late 1980s.
Contrary to a naïve view that firms with high debt gain during the bubble period by the use of extensive leverage, the analysis of our purified version of q value reveals that firms with less debt are indeed higher quality firms. Because we measure equity by market values, it may also mean that firms with high stock price and little debt become quality firms. Again, it warns us to use the conventional q where the debt tax shield effect is simultaneously included, and justifies the use of our constructed unlevered q. The pattern of realized returns seen in Figure 5 in relation to the changes in corporate tax rates and capital tax rates is also similar to the one found in Figure 3, but again the difference is wider between the two portfolios, especially in recent years.
Finally, Figure 6 highlights the trend and cyclical components of our unlevered q value using the HodrickPrescott filter [40] with the lambda value of 400 applied to our monthly estimates of the unlevered q values. There is not much difference in the trend variation patterns between the two sectors, although the cyclical swings are larger for the consumption goods sector as Table 1 reveals. It is also what was a priori expected, because this sector produces the end product. More importantly, however, we find that unlevered q values lead the contraction and expansion periods of the actual economy with one to two year lengths. It suggests that our unlevered q value can also predict future business cycle swings at two business sectors. Moreover, note we observe the decrease of the trend component of the unlevered q in the most recent year of 2007. Hence, even though the subprime meltdown of September 2008 had not occurred, we can say that the Japanese economy was into downturn from this figure. It is noteworthy when we extract only the real productivity part of Tobin’s q as we derived our general equilibrium solution.
5. Conclusions
The paper addresses a question of how taxation affects the equity cost of capital, the value of firms, and the quality of firms as measured by Tobin’s q. Our model extends the two-sector model developed by Christiano and Fisher (1995), introducing tax parameters and government budget identity equations. We derive the firm’s total value and the unlevered q by removing the effect of debt tax shield benefits in order to highlight real productivity of firms. We assume homogenous expectations for capital market agents and labor immobility as was the case with [1]. Given our equilibrium solutions, we conduct some limited comparative static analysis with respect to the changes in corporate tax rates and firms’ leverage ratios, and, in an empirical part of the paper, we thoroughly investigate the time-series behavior of unlevered q-values with special considerations to the characteristic differences of firms’ effective marginal tax rates and firms’ debt-to-total-asset ratios. We confirm the importance of distinguishing real productivity and the tax shield effect with Japanese data. Note during which time we pay particular attention to the phases of business cycles and changes in actual corporate tax rates in Japan.
Overall, we confirm the validity of our theory of using our unlevered q measure. In addition, the result gives us a warning against using the conventional Tobin’s q without caution because both the real productivity element and another element from financing decisions are jointly included.

Figure 6. The decomposition of unlevered q by H-P filter (λ = 400).
Finally, we recommend using our constructed unlevered q-values when the researcher wants to identify the real productivity of firms. The tax authority also has to take this into consideration when changing tax rates, either to increase or decrease tax collections and the consequent public infrastructure investment. The further calibration exercise to complement our simple comparative static analysis is a subject for our future work.
6. Acknowledgements
This paper was presented at the 2010 European Economic Association, the 2009 Congress of the International Institute of Public Finance, and the 2009 Japan Finance Association Meeting. The authors thank Georg Wamser and Keiichi Hori for their comments to improve the paper.
REFERENCES
- L. J. Christiano and J. D. M. Fisher, “Tobin’s q and Asset Returns: Implications for Business Cycle Analysis,” Staff Report 200, Federal Reserve Bank of Minneapolis, 1995.
- E. R. McGrattan and E. C. Prescott, “Taxes, Regulations, and the Value of U.S. and U.K. Corporations,” Review of Economic Studies, Vol. 72, No. 3, 2005, pp. 767-796. http://dx.doi.org/10.1111/j.1467-937X.2005.00351.x
- S. A. Ross, “The Determination of Financial Structure: The Incentive-Signaling Approach,” Bell Journal of Economics, Vol. 8, No. 1, 1976, pp. 23-40. http://dx.doi.org/10.2307/3003485
- E. B. Lindberg and S. A. Ross, “Tobin’s q and Industrial Organization,” Journal of Business, Vol. 54, No. 1, 1981, pp. 1-32.
- F. Degeorge, B. Moselle and R. Zeckhauser, “The Ecology of Risk Taking,” Journal of Risk and Uncertainty, Vol. 28, No. 3, 2004, pp. 195-215. http://dx.doi.org/10.1023/B:RISK.0000026095.75015.e0
- A. J. Auerbach, “Taxation and Corporate Financial Policy,” In :A. J. Auerbach and M. Feldstein, Eds., Handbook of Public Economics, Vol. 3, Elsevier Science, Amsterdam, 2002, pp. 1251-1292. http://dx.doi.org/10.1016/S1573-4420(02)80023-4
- P. A. Samuelson, “Tax Deductibility of Depreciation to Insure Invariant Valuation,” Journal of Political Economy, Vol. 72, No. 6, 1964, pp. 604-606. http://dx.doi.org/10.1086/258967
- L. H. Summers, “Taxation and Corporate Investment: A q-Theory Approach,” In: W. C. Brainard and G. L. Perry, Eds., Brookings Paper on Economic Activity 1, The Brookings Institution, Washington DC, 1981, pp. 67-127.
- K. Kubota, S. Saito and H. Takehara, “Corporate Investment, Interest Tax Shields, Taxation, and Tobin’s q: Business Cycle Analysis of Japanese Industries and Firms,” Journal of Strategic Management Studies, Vol. 4, No. 1-2, 2013, pp. 27-45.
- A. Yakita, “Capital Taxation, Tobin’s q and Overlapping Generations,” Japanese Economic Review, Vol. 51, No. 1, 2000, pp. 111-129. http://dx.doi.org/10.1111/1468-5876.00142
- F. Hayashiand T. Inoue, “The Relation between Firm Growth and Q with Multiple Capital Goods: Theory and Evidence from Panel Data on Japanese Firms,” Econometrica, Vol. 59, No. 3, 1991, pp. 731-753. http://dx.doi.org/10.2307/2938226
- K. Hori, M. Saito and K. Ando, “What Caused Fixed Investment to Stagnate during the 199s in Japan? Evidence from Panel Data of Listed Companies,” The Japanese Economic Review, Vol. 57, No. 2, 2006, pp. 283-306. http://dx.doi.org/10.1111/j.1468-5876.2006.00366.x
- K. H. Chung and S. W. Pruitt, “A Simple Approximation of Tobin’s q,” Financial Management, Vol. 23, 1994, pp. 70-74. http://dx.doi.org/10.2307/3665623
- S. B. Perfect and K. W. Wiles, “Alternative Constructions of Tobin’s q: An Empirical Comparison,” Journal of Empirical Finance, Vol. 1, No. 3-4, 1994, pp. 313-341. http://dx.doi.org/10.1016/0927-5398(94)90007-8
- T. Erickson and T. M. Whited, “On the Accuracy of Different Measures of Q,” Financial Management, 2006, pp. 5-33. http://dx.doi.org/10.1111/j.1755-053X.2006.tb00145.x
- K. Kubota and H. Takehara, “Changes in Factor Loading across Sectors and Economic Dynamics: Evidence for the Japanese Firms,” 2004. http://ssrn.com/abstract=686562 http://dx.doi.org/10.2139/ssrn.686562
- J. R. Graham, “Debt and the Marginal Tax Rate,” Journal of Financial Economics, Vol. 41, No. 3, 1996, pp. 41-73. http://dx.doi.org/10.1016/0304-405X(95)00857-B
- W. F. Brock, “Asset Prices in a Production Economy,” In: J. J. McCall, Ed., The Economics of Information and Uncertainty, University of Chicago Press, Chicago, 1982.
- J. C. Cox, J. E. Ingersoll and S. A. Ross, “An Intertemporal General Equilibrium Model of Asset Prices,” Econometrica, Vol. 53, No. 2, 1985, pp. 139-170. http://dx.doi.org/10.2307/1911241
- J. Cochrane, “A Cross-Sectional Test of an InvestmentBased Asset Pricing Theory,” Journal of Political Economy, Vol. 104, No. 3, 1996, pp. 572-621. http://dx.doi.org/10.1086/262034
- M. Boldrin, L. J. Christiano and J. D. M. Fisher, “Asset Pricing Lessons for Modeling Business Cycles,” Working Paper, No. 560, Federal Reserve Bank of Minneapolis, 1995.
- M. L. Boldrin, L. J. Christiano and J. D. M. Fisher, “Habit Persistence, Asset Returns, and the Business Cycles,” Staff Report, No. 280, Federal Reserve Bank of Minneapolis, 2000.
- J. Y. Campbell and L. M. Viceira, “Strategic Asset Allocation,” Oxford University Press, Oxford, 2002. http://dx.doi.org/10.1093/0198296940.001.0001
- R. E. Lucas Jr. and E.C. Prescott, “Investment under Uncertainty,” Econometrica, Vol. 39, No. 5, 1971, pp. 659- 681. http://dx.doi.org/10.2307/1909571
- G. M. Constantinides and M. Scholes, “Optimal Liquidation of Assets in the Presence of Personal Taxes: Implications for Asset Pricing,” Journal of Finance, Vol. 35, No. 2, 1980, pp. 439-449. http://dx.doi.org/10.1111/j.1540-6261.1980.tb02174.x
- M. H. Miller, “Debt and Taxes,” Journal of Finance, Vol. 32, No. 2, 1977, pp. 261-75.
- J. R. Graham, “How Big Are the Tax Benefit of Debt?” Journal of Finance, Vol. 55, No. 5, 2000, pp. 1901-1942. http://dx.doi.org/10.1111/0022-1082.00277
- M. T. Leary and M. R. Roberts, “Do Firms Rebalance Their Capital Structures?” Journal of Finance, Vol. 60, No. 6, 2005, pp. 2575-2619. http://dx.doi.org/10.1111/j.1540-6261.2005.00811.x
- M. L. Lemmon, M. R. Roberts and J. F. Zender, “Back to the Beginning: Persistence and the Cross-Section of Corporate Capital Structure,” 2006. http://ssrn.com/abstract=881899 http://dx.doi.org/10.2139/ssrn.881899
- H.-W. Sinn, “Taxation and the Cost of Capital: The ‘Old’ View, the ‘New’ View, and Another View,” In: D. Bradford, Ed., Tax Policy and the Economy, Vol. 5, MIT Press, Massachusetts, 1991, pp. 25-54.
- E. R. Arzac and L. G. Glosten, “A Re-Consideration of Tax Shield Valuation,” Mimeo, Graduate School of Business, Columbia University, 2004.
- M. Scholes, M. A. Wilson, M. Erickson, E. M. Maydew and T. Shevin, “Taxes and Business Strategy,” 2nd Edition, Prentice Hall, Upper Saddle River, 2002.
- M. King and D. Fullerton, “The Taxation of Income from Capital,” The University of Chicago Press, Chicago and London, 1984.
- J. G. Cummins, T. S. Harris and K. A. Hasssett, “Accounting Standards, Information Flow, and Firm Investment Behavior,” NBER Working Paper, No. 4685, 1994.
- V. Kanniainen and J. Sodersten, “The Importance of Reporting Conventions for the Theory of Taxation,” Journal of Public Economics, Vol. 57, No. 3, 1995, pp. 417-430. http://dx.doi.org/10.1016/0047-2727(95)80004-S
- K. Kubota and H. Takehara, “Effect of Tax Rate Changes on the Cost of Capital: The Case of Japanese Firms,” Finanz Archiv/Public Finance Analysis, Vol. 63, No. 2, 2007, pp. 163-185.
- E. F. Fama and K. R. French, “Industry Cost of Equity,” Journal of Financial Economics, Vol. 43, No. 2, 1997, pp. 1939-1967. http://dx.doi.org/10.1016/S0304-405X(96)00896-3
- M. Honma, N. Atoda, F. Hayashi and K. Hata, “Capital Investment and Corporate Taxation (in Japanese),” Research Series No. 41, the Cabinet Ministry of Japan (Formerly Economic Planning Agency), 1984.
- J. Mirrlees, “An Exploration in the Theory of Optimal Taxation,” Review of Economic Studies, Vol. 38, No. 2, 1971, pp. 175-208. http://dx.doi.org/10.2307/2296779
- R. J. Hodrick and E. C. Prescott, “Post-War US Business Cycles: An Empirical Investigation,” Journal of Money, Credit, and Banking, Vol. 29, No. 1, 1997, pp. 1-16. http://dx.doi.org/10.2307/2953682
Appendix
We solve for Equations (5), (6), (19), (20), (21), (22) and (27), and derive our general equilibrium solution and then derive our unlevered Tobin’s q and rate of return of the stock.
From (5) and (6) in the main text we get the following.
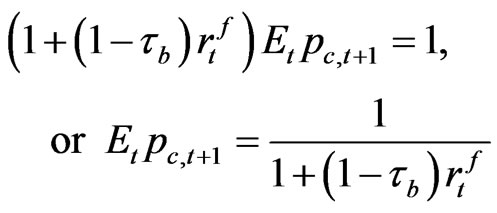 (A-1)
(A-1)
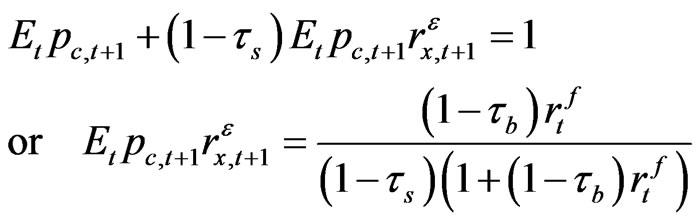 (A-2)
(A-2)
Then, 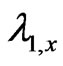 in (21) can be solved as follows where the after tax interest rate
in (21) can be solved as follows where the after tax interest rate 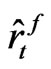 is defined as
is defined as 
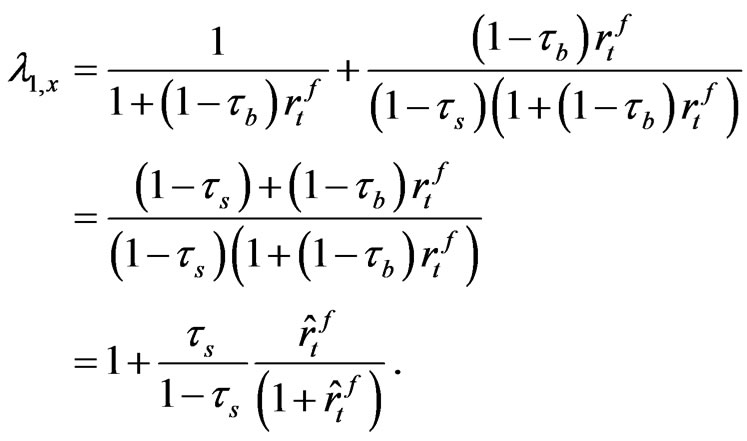 (A-3)
(A-3)
Let us define  as
as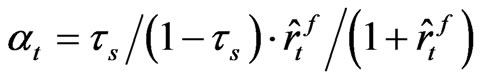 . Then, we can also solve for
. Then, we can also solve for 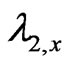 as follows. Using (A-1) and (22) in the main text we get
as follows. Using (A-1) and (22) in the main text we get
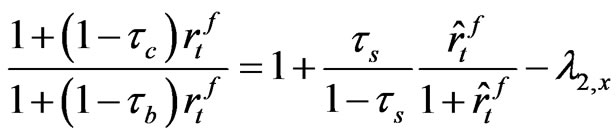 (A-4)
(A-4)
Then,
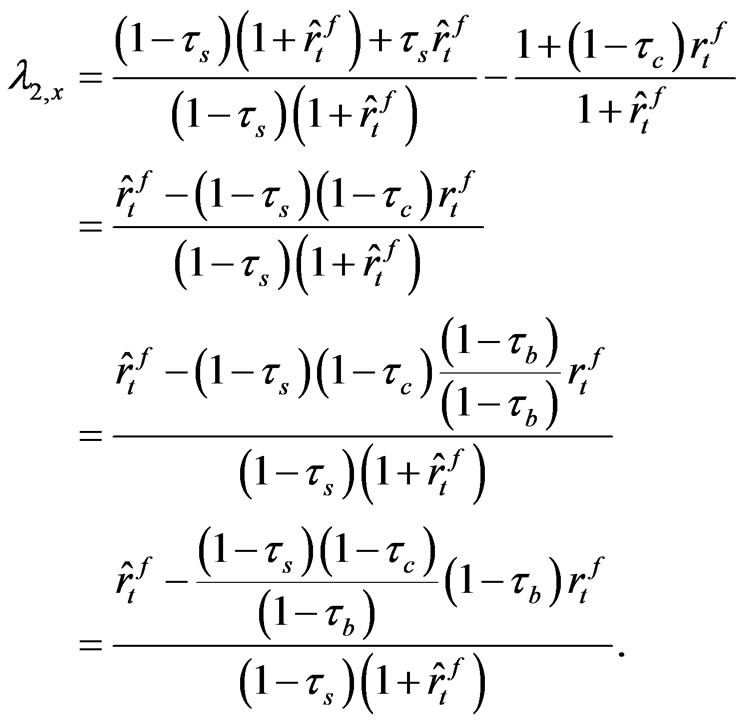 (A-5)
(A-5)
and using the definition of g in (12) of the main text we obtain
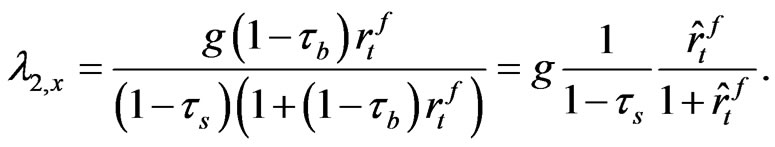 (A-6)
(A-6)
Then, (20) can be expressed as follows.
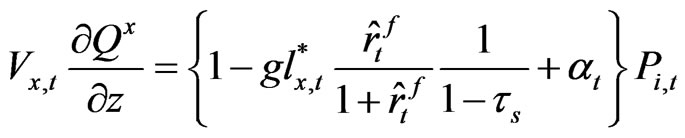 (A-7)
(A-7)
Thus, we get a following (A-8) by which we obtain the q ratio in (25) of the main text.
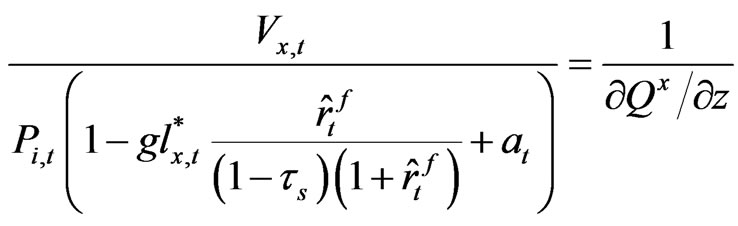 (A-8)
(A-8)
Next, from (22) we have
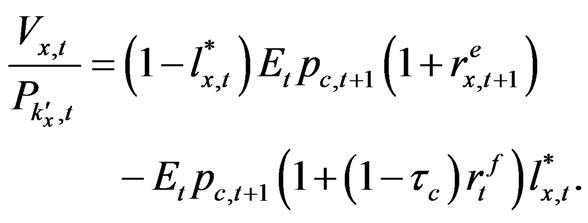 (A-9)
(A-9)
Applying (17) of the main text we get
 (A-10)
(A-10)
The Ex ante zero profit condition should be satisfied if the following holds under all states of time period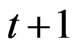 .
.
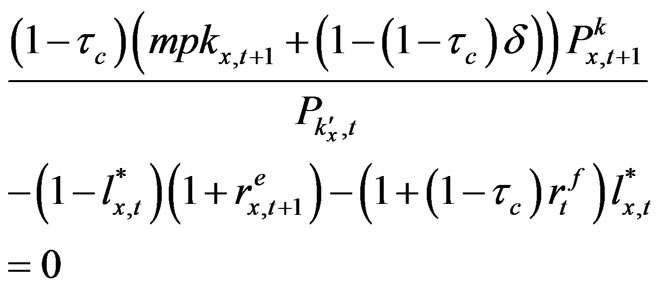 (A-11)
(A-11)
After some algebraic manipulations using 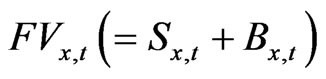 , we get
, we get
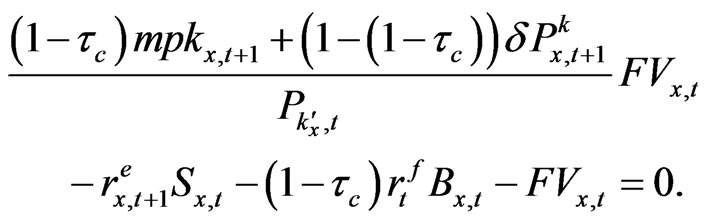 (A-12)
(A-12)
Thus, we get Equations (24) and (30) in the main text.
NOTES
1A partial equilibrium analysis in which a household’s optimization problem is suppressed is conducted in [9]. Also, [10] analyzes the similar problem using the overlapping generation model with capital adjustment costs. However, [10] does not incorporate individual taxations as ours.
2The calibration results using U.S. data are demonstrated in [1]. The empirical result that estimates the cost of equity for different business sectors for Japanese data is reported by [16].
3It is also to keep intact the basic original mode in [1] and to concentrate on effects of taxation on Tobin’s q in a simple framework.
4The formulation can be extended to the power utility case with habit formation as in [22], but we only adopt the log utility case for simplicity. The role of the log utility and the power utility with various risk aversion coefficients in long-term asset allocation decisions are well discussed in [23].
5This usage follows [2], in which the authors introduce the government subsidy via investment tax credit and accelerate depreciations over economic depreciation. We also abstract from the difference between the postponed and realized capital gain tax and the accrued capital gain tax.
6Because in Japan the interest income tax is the constant withheld tax, this abstraction does not affect the rest of our analysis.
7The original functional forms of (1) and (3) are as found in [24], equations (10) and (11) in which the investment goods adjustment cost was first introduced.
8The average tax rate for holding stock should reflect effective rates of the capital gain tax triggered by the deferred optimal liquidation of stocks by investors. See [25], for example.
9We thank George Constantinides for discussion of this point.
10In [2], they maximize the present value of firm distributions after individual tax payment for stockholders. We do not take this path in the paper, but this way of specification is subject to future scrutiny.
11This is also similar to the economic value maximization criterion in corporate finance literature.
12Because of the labor immobility assumption in this paper as in [1] the current labor decision is the pre-commitment to the next period’s labor work input.
13See Appendix for a formal derivation.
14See, for example, [28,29] for evidence of the persistence of capital structure for U.S. firms.
15Here it also includes the capital windfall gain emanating from the debt tax benefit.
16Although it is not a complete static analysis of the system of equations (11), numerical calibrations of this simultaneous system are left outside the scope of this paper.
17Note this formulation is similar to the new share issue and the stock repurchase category in Table 1 of [30]. Our formulation should be also categorized as the “Old” view.
18Because we assume stationary equilibrium the debt amount is assumed to stay constant and we discount with the risk free rate. However, it is appropriate to discount with the unlevered cost of equity when the debt amount changes every period. See [31] for discussion.
19See [30] again for extensive analyses of the relationship between before and after-tax cost of capital.
20Because [15] discuss that all q measurement methods are subject to estimation errors, we choose this simplest and most widely used method.
21Note it is slightly different from the definition used by [33].
22Only the financial reports are observable at the individual firm level in Japan and individual tax returns are not.
23Japanese financial reporting and tax reporting are prepared according to the uniform system. Moreover, from fiscal year 1999 the tax deferral account in balance sheets are admitted to be recorded on the condition that such a deferred amount can be expected to be reversed with a high probability. In spite of this allowance, the Japanese taxation system is still uniform reporting in the sense that depreciation methods, inventory costing, or other major accounting choices have to follow uniform reporting. See also [34,35] for a related discussion on the Japanese taxation system.
24During our sampling period, the firms which experienced losses less than 5 years ago, the tax loss carry forward benefits accrue and hence we decided to extend our simulations after 5 years from today for the period of 20 years to take care of this cumulative effect. Similar results are reported in [36] with some simulation results of the tax rate changes. Note the current tax law allows for an extension up to 7 years.
25To be precise, we should discount it with the risky corporate bond yield for each firm to get a correct present value. However, exact bond yield data for all sample firms are not available. An example of using the government bond rate as a base and adding the risk premium as specified by the statutory code is found in the Swedish tax code, but the Japanese tax code does not deal with this risk premium concept.
26The recommendations to include the tax deferral accounts in accounting standards in Japan was released on October 30, 1998 and enacted in April 1999, while some firms began their voluntary disclosure in April 1998.
27Note that more than 90 percent of Japanese firms choose their fiscal year end at the end of March. As in the U.S., Japanese companies have to file tax returns within three months after the fiscal year-end at the latest. Statutory deadline is two months and can be postponed to three months, which most Japanese firms choose in accordance with the deadline of their proxy statements.
28Because we use book value of total assets in the denominator, the consumption goods sector with less capital intensity might have a smaller total assets balance. It may be one of the reasons, but we do not conclude here.
29The relative tax rates matter here (see [30]).

