Journal of Mathematical Finance
Vol.3 No.4(2013), Article ID:38144,5 pages DOI:10.4236/jmf.2013.34044
Contingent Claims in Incomplete Markets: A Case Study
Division of Actuarial Science, School of Management Studies, University of Cape Town, Cape Town, South Africa
Email: sure.mataramvura@uct.ac.za
Copyright © 2013 Sure Mataramvura. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received July 2, 2013; revised August 11, 2013; accepted August 27, 2013
Keywords: incomplete markets; equivalent martingale measure; admissible pricing measure
ABSTRACT
In this paper, we revisit pricing contingent claims in incomplete markets. While a lot have been done on pricing in incomplete markets, there is still a gap on the categorization of the payoffs. Some contingent claims are attainable while others will not be attainable. We address the question of which contingent claims belong to each group. We also propose a generalization of the equivalent martingale measures used for pricing, a generalization which includes those studied so far. We also provide some examples of how to price in each class and introduce important definitions.
1. Introduction
In this paper we extend the study of the pricing of contingent claims in incomplete markets. We categorize these contingent claims into those which are attainable and those which are not attainable which has not been fully addressed in previous works. In a market where there are more Brownian motions than number of stocks the market is likely to be incomplete. We refer the reader to [1] for more discussion on incompleteness of markets of this type. The Girsanov theorems give an explicit representation of the market price of risk which induces the equivalent martingale measure used for pricing. In incomplete markets there are infinitely many such equivalent martingale measures, leaving researchers looking for what could be a good candidate measure for pricing. Common examples of these measures  are the minimal martingale measure as in [2], the relative entropy minimizer as in [3], the Esscher transform in [4], the minimal
are the minimal martingale measure as in [2], the relative entropy minimizer as in [3], the Esscher transform in [4], the minimal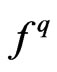 —divergence as in [5] among others.
—divergence as in [5] among others.
One objective for this study is to generalize these measures to include even those measures not yet studied. We call these measures admissible pricing measures. We note that the mapping from the set of equivalent martingale measures to the price of contingent claims is a many to one mapping. Therefore there are some contingent claims which have a unique price calculated using different equivalent martingale measures. We do this by means of some simple toy examples that reveal our results. It is in this light that the uniqueness of some of the admissible pricing measures suggested before could be brought into question. However, if we introduce an equivalence relation which results in cosets, each containing admissible pricing measures that gives the same price for a given contingent claim, then this mapping becomes an injective function. We have limited this ideas into the idealizations and we leave further scrutny to interested readers.
This paper is organized as follows: the next section gives the preliminaries. In that we also introduce some important definitions. The final chapter deals with the important results where we observe that the pricing measures are not unique after all. This is achieved through some toy examples of European options belonging to the sets of attainable claims and non-attainable claims respectively.
2. Mathematical Preliminaries
Assume that we have a filtered probability space
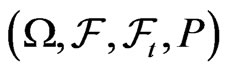
with the filtration chosen in such a way that asset prices are  -adapted. Consider a market
-adapted. Consider a market

where  is the price of the bond at time
is the price of the bond at time  and is given by
and is given by
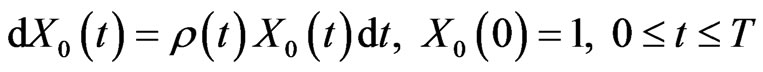 (2.1)
(2.1)
where  is the interest rate and for
is the interest rate and for 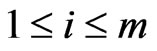 the price of stock
the price of stock 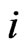 is given by
is given by
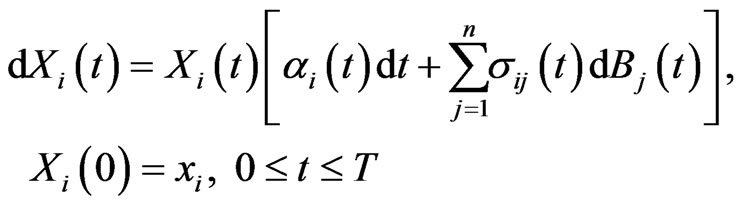 (2.2)
(2.2)
where

is an n-dimensional P-Brownian motion and  means transposition. We can write (2.2) as
means transposition. We can write (2.2) as
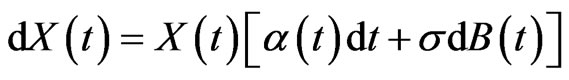
where
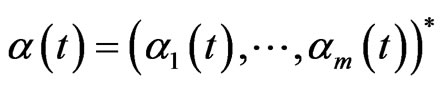
is the vector of appreciation rates and
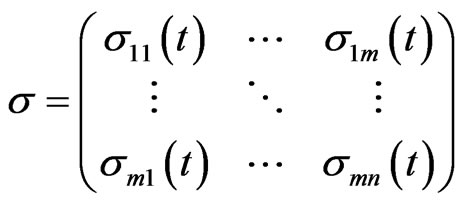
is the volatility matrix. Assume that 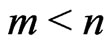 and rank
and rank  so that
so that 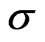 has no left inverse. It is then clear from this setup that the market of stocks and bonds is incomplete (see [1]).
has no left inverse. It is then clear from this setup that the market of stocks and bonds is incomplete (see [1]).
By the Girsanov theorem for this market (see [1]), the market price of risk is  such that
such that
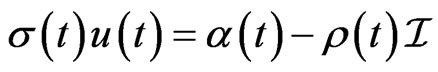
where 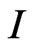 is the 1-vector in
is the 1-vector in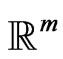 . The system (2.3) has infinitely many solutions in
. The system (2.3) has infinitely many solutions in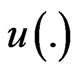 . By the same Girsanov theorems cited above, the probability measure Q given by
. By the same Girsanov theorems cited above, the probability measure Q given by
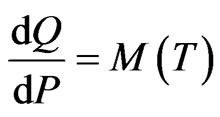
where
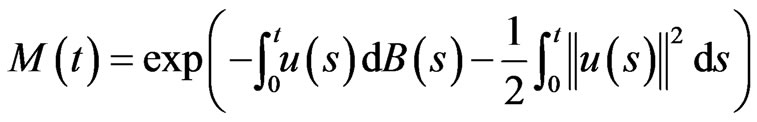
is equivalent to P and is such that
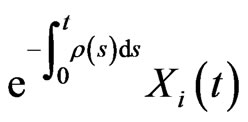
is a Qmartingale. In this case 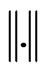 represents the usual norm in
represents the usual norm in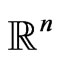 . Moreover
. Moreover 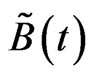 given by
given by
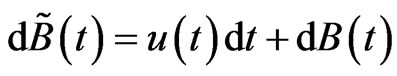
is a Q-Brownian motion. Surely there are infinitely many equivalent martingale measures Q. Let 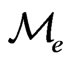 be the set of all equivalent martingale measures Q for this market.
be the set of all equivalent martingale measures Q for this market.
Pricing a contingent Tclaim with payoff 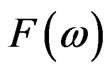 in such a market has been studied before. The most common ideas include either to complete the market (see [6]) or finding a measure
in such a market has been studied before. The most common ideas include either to complete the market (see [6]) or finding a measure 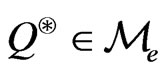 which is “good” enough so that
which is “good” enough so that
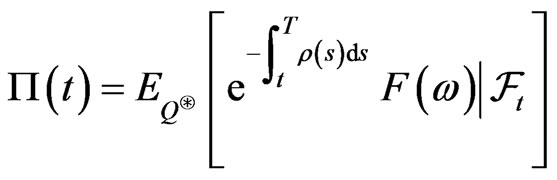
is the “best” price admissible to buyers and sellers. It is known (see [1] and references therein) that
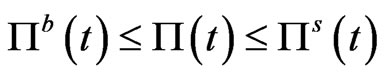
where respectively 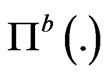 and
and 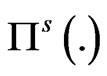 represents the buyer's price and seller’s price. The interval
represents the buyer's price and seller’s price. The interval
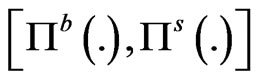
is the set of admissible prices for both buyers and sellers. Any price charged outside this interval will cause one to create an arbitrage. In [1], the authors give an explicit representation of 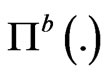 and
and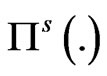 .
.
In this paper we aim to characterize and price contingent claims in incomplete markets. We will characterize them into those which are attainable and those which are not and we give an overview of their pricing procedure.
3. Ontingent Claims in Incomplete Markets
We look at the following results:
Proposition 3.1 Let 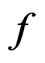 be a measurable function and T
be a measurable function and T  0 be a finite time horizon. Any contingent Tclaim of the form
0 be a finite time horizon. Any contingent Tclaim of the form
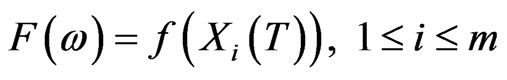
is attainable in the market, its price is unique and is independent of the choice of the equivalent martingale measure Q.
Proof:
Without loss of generality, let us assume constant coefficients. With respect to P, we have
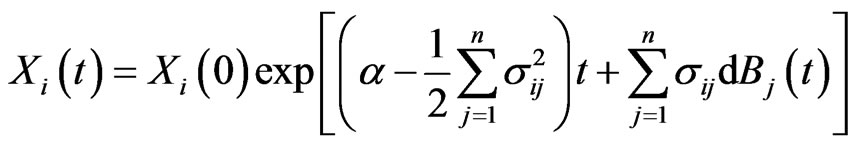
and with respect to Q we have
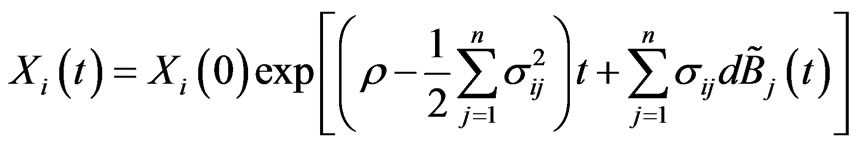
Clearly, 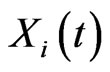 is independent of the market price of risk
is independent of the market price of risk  and thus is independent of the equivalent martingale measure Q, so that the price
and thus is independent of the equivalent martingale measure Q, so that the price
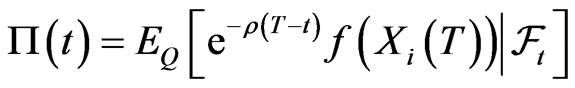 (3.1)
(3.1)
is independent of Q. Thus 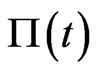 is uniquely determined in (3.1). To show that every
is uniquely determined in (3.1). To show that every 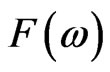 of this nature is attainable, it is enough to use the martingale representation theorem and also normalize to get a martingale representation of the terminal value of the self-financing portfolio of stocks and bonds. We refer the reader to [1] Chapter 12 for details of this working.
of this nature is attainable, it is enough to use the martingale representation theorem and also normalize to get a martingale representation of the terminal value of the self-financing portfolio of stocks and bonds. We refer the reader to [1] Chapter 12 for details of this working.
N.B: What the proposition above tells us is that in incomplete markets the set of attainable claims is not empty. So in incomplete markets there are some contingent claims which can be hedged by a portfolio of stocks and bonds. Let 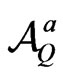 be the set of all T-claims which are attainable in this market. Therefore
be the set of all T-claims which are attainable in this market. Therefore
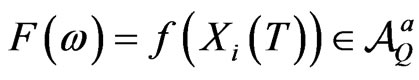 .
.
we are not so certain as to what other types of payoff are in  and this remains a good exercise for interested readers.
and this remains a good exercise for interested readers.
Proposition 3.2 Let 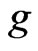 be a measurable function, then any T-claim with payoff
be a measurable function, then any T-claim with payoff
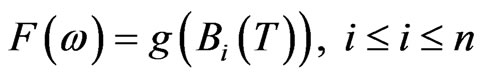
is not attainable in the market.
The proof is in [1] Chapter 12 for a particular case which could easily be generalized. The set of T-claims which are not attainable in the market shall be denoted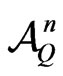 .
.
Definition 3.3 An equivalent martingale measure  is called an admissible pricing martingale measure for the T-claim
is called an admissible pricing martingale measure for the T-claim 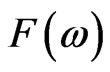 if
if
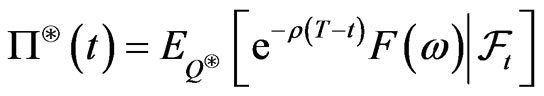
is admissible to buyers and sellers and there exist utility functions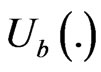 , (the buyer’s utility) and
, (the buyer’s utility) and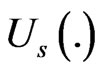 , (the seller’s utility) such that
, (the seller’s utility) such that
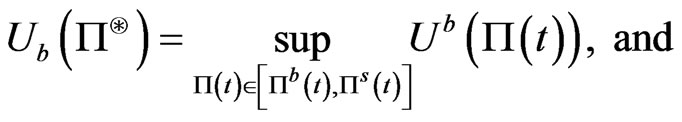 (3.2)
(3.2)
 (3.3)
(3.3)
Note that (3.2) and (3.3) can easily be justified through an auction of the contingent claim  and the price for this claim obtained through such an auction is
and the price for this claim obtained through such an auction is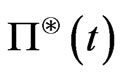 . Therefore for each contingent claim
. Therefore for each contingent claim 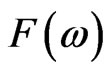 there is a unique price
there is a unique price 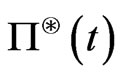 admissible to buyers and seller and there exists an admissible pricing measure
admissible to buyers and seller and there exists an admissible pricing measure  such that
such that
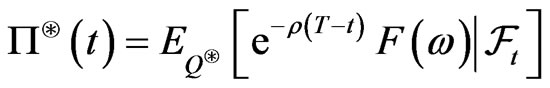 .
.
what may not be clear for now is whether this admissible pricing measure is unique for each contingent claim. This will be addressed later after looking at the following particular cases.
3.1. Examples of Pricing in  and
and 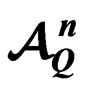
We assume constant coefficients and assume 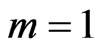 and
and . We also consider the mean-variance measure as one of the studied admissible pricing measures. The choice of this measure is arbitrary since the results for the other already studied pricing measures will be similar.
. We also consider the mean-variance measure as one of the studied admissible pricing measures. The choice of this measure is arbitrary since the results for the other already studied pricing measures will be similar.
The market will now be 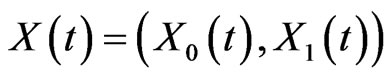 with
with
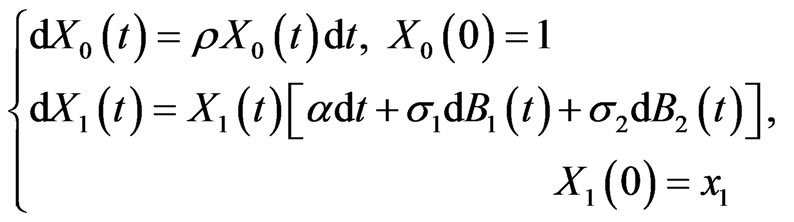 (3.4)
(3.4)
Then by the Girsanov theorem, the market price of risk is 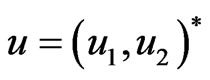 such that
such that
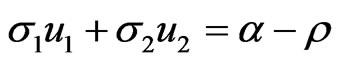 (3.5)
(3.5)
There are infinitely many solutions for  and
and . The measure Q given by
. The measure Q given by
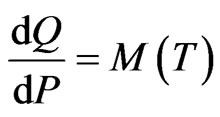
where
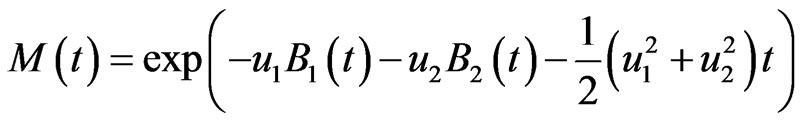
is an equivalent martingale measure such that 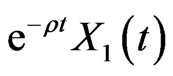 is a Q-martingale. Moreover,
is a Q-martingale. Moreover,
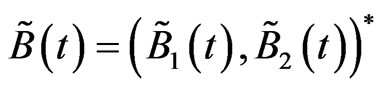
given by
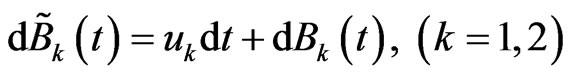
is a two dimensional Brownian motion with respect to Q.
Since 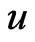 induces Q then there are infinitely many equivalent martingale measures to P. Any payoff
induces Q then there are infinitely many equivalent martingale measures to P. Any payoff  will have infinitely possible prices . The challenge is to find the “best” such price admissible to buyers and sellers.
will have infinitely possible prices . The challenge is to find the “best” such price admissible to buyers and sellers.
3.1.1. Pricing a Payoff in 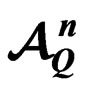 by the Mean Variance Martingale Measure
by the Mean Variance Martingale Measure
Let us for simplicity consider the European T-claim with payoff
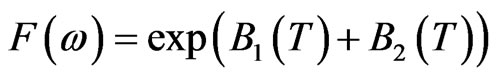 .
.
then with respect to Q, we have
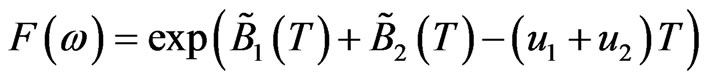 .
.
the mean variance equivalent martingale measure  is the one which minimizes
is the one which minimizes
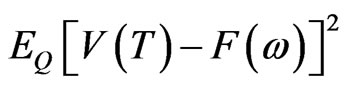
over all 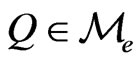 where
where 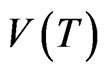 is the terminal value of a self financing portfolio
is the terminal value of a self financing portfolio 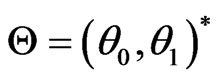 of stocks and bonds. We have
of stocks and bonds. We have

and
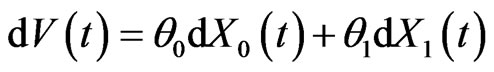 .
.
Therefore to get  we find
we find
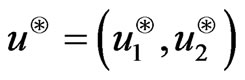
from
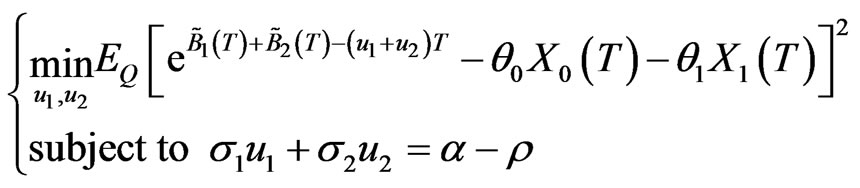
Therefore 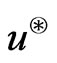 is obtained from the following system of equations
is obtained from the following system of equations
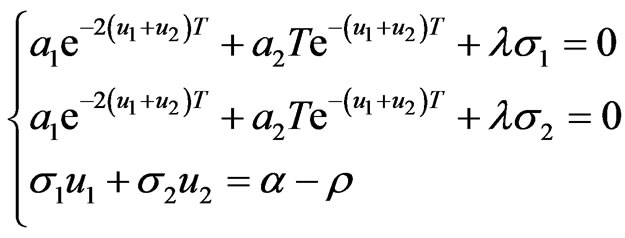 (3.6)
(3.6)
where 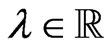 is the Lagrange multiplier.
is the Lagrange multiplier.
Here  and
and
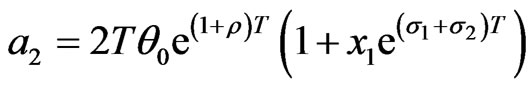
Solving we get
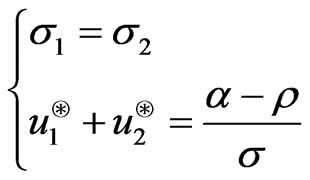 (3.7)
(3.7)
where 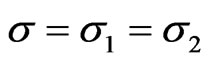
Therefore, with respect to , we have
, we have
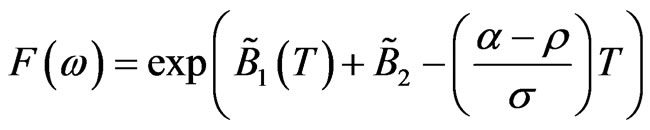 .
.
We see here that  is uniquely determined by (3.7). The price of the contingent claim
is uniquely determined by (3.7). The price of the contingent claim 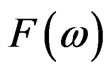 is
is
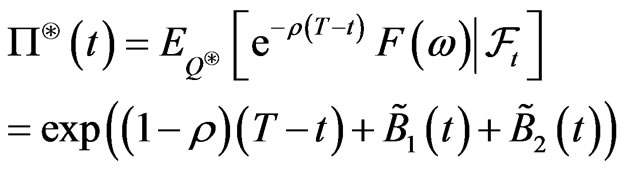 .
.
In particular if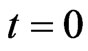 , then
, then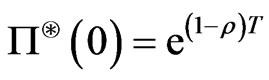 .
.
Remark 3.4 If instead, we consider
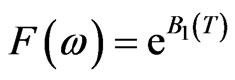
then we get the solution
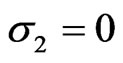 ,
, 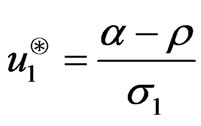 ,
, 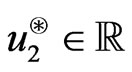
is arbitrary. Therefore in this case the mean variance measure is not unique since 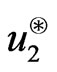 can take any value in
can take any value in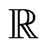 .
.
The price for this contingent claim is
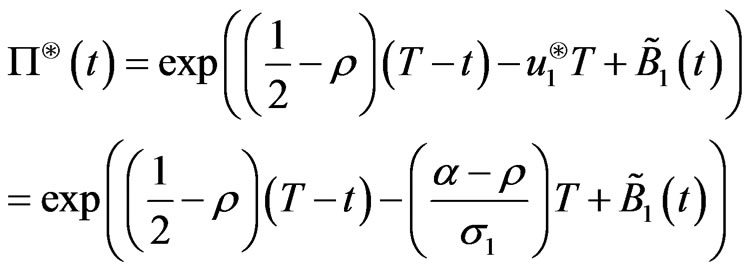
and is independent of the choice of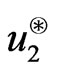 .
.
In particular to these toy examples, we see that if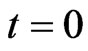 , then
, then
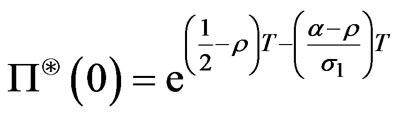 .
.
In conclusion, we see that in , each chosen contingent claim has a unique price calculated using either a unique or infinitely many admissible pricing measures. So the mapping from the set of admissible pricing measures to the set of admissible prices can be a many to one mapping.
, each chosen contingent claim has a unique price calculated using either a unique or infinitely many admissible pricing measures. So the mapping from the set of admissible pricing measures to the set of admissible prices can be a many to one mapping.
3.1.2. Pricing a Payoff in  by the Mean Variance Martingale Measure
by the Mean Variance Martingale Measure
Let us now consider a payoff of the form
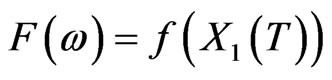
and in particular let f be the identity function so that
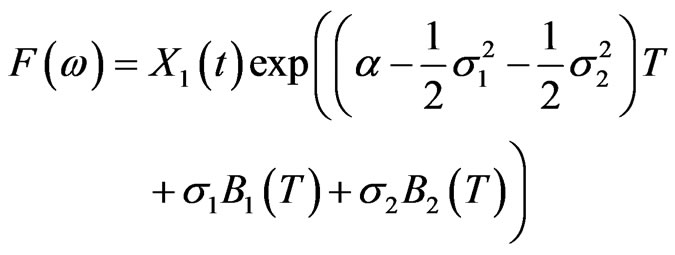 .
.
With respect to Q, we have

which does not depend on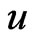 . Therefore the mean variance measure
. Therefore the mean variance measure  does not depend on
does not depend on 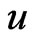 meaning that any choice of
meaning that any choice of 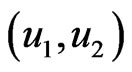 will reult in the same price for F, which price is
will reult in the same price for F, which price is

and if , then
, then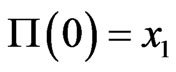 , the price of the stock. Therefore a European contingent claim which promises to pay the terminal stock price should charge the current stock price.
, the price of the stock. Therefore a European contingent claim which promises to pay the terminal stock price should charge the current stock price.
Definition 3.5 Two admissible pricing measures  and
and 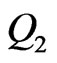 are substitutes with respect to a given payoff
are substitutes with respect to a given payoff 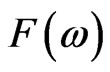 if and only if the discounted price of
if and only if the discounted price of  with respect to
with respect to 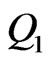 is the same as that with respect to
is the same as that with respect to 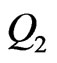
Remark 3.6 The relationship substitutes defined above is an equivalence relation.
The proof of this remark is trivial. Now the equivalence relation would result in the creation of equivalent classes and considering 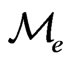 as a set of these atoms, then the map from
as a set of these atoms, then the map from 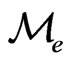 to
to 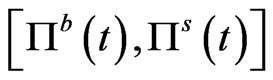 will be an injective function. We are not interested in pursuing this algebraic reality in this paper and leave it for interested readers to explore further.
will be an injective function. We are not interested in pursuing this algebraic reality in this paper and leave it for interested readers to explore further.
In conclusion to this section, we have managed to categorize payoffs which are attainable and those which are not in an incomplete market. Each payoff will be priced using an admissible pricing measure. Our definition of admissible pricing measures shows that any contingent claim in incomplete markets can be priced and the price is unique. However the uniqueness of the price does not imply the uniqueness of the pricing measure. For example, if the payoff is attainable, then all 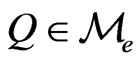 yields the same price. The story is different in the case that the claim is not attainable.
yields the same price. The story is different in the case that the claim is not attainable.
4. Conclusion
We have managed to categorize the T-claims which are attainable and those which are not and we have linked each payoff to a price which in turn is linked to a class of substitutes. Therefore, given a contingent claim, we should be able to find its price using one of the admissible pricing measures. The price is calculated as the discounted expectation of the payoff with respect to the admissible measure and buyers and sellers would always agree on this price.
REFERENCES
- B. Oksendal, “Stochastic Differential Equations,” 6th Edition, Springer-Verlag, Berlin, 2007.
- M. Schweizer, “On the Minimal Martingale Measure and the Möllmer-Schweizer Decomposition,” Stochastic Analysis and Applications, Vol. 13, No. 5, 1995, pp. 573-599. http://dx.doi.org/10.1080/07362999508809418
- M. Fritelli, “The Minimal Entropy Martingale Measure and the Valuation Problem in Incomplete Markets,” Mathematical Finance, Vol. 10, No. 1, 2000, pp. 39-52. http://dx.doi.org/10.1111/1467-9965.00079
- H. U. Gerber and E. S. W. Shi, “Option Pricing by Esscher Transforms,” Transactions of the Society of Actuaries, Vol. 46, 1994, pp. 99-191.
- M. Jeanblanc, S. Klöppel and Y. Miyahara, “Minimal
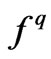 -Martingale Measures for Exponential Lévy Processes,” The Annals of Applied Probability, Vol. 17, No. 5-6, 2007, pp. 1615-1638. http://dx.doi.org/10.1214/07-AAP439
-Martingale Measures for Exponential Lévy Processes,” The Annals of Applied Probability, Vol. 17, No. 5-6, 2007, pp. 1615-1638. http://dx.doi.org/10.1214/07-AAP439 - S. Mataramvura, P. Dankemlmann and S. W. Mgobhozi, “Completion of Markets by Variation Processes,” Working Paper, 2013.

