ABSTRACT

This paper establishes a dynamic portfolio insurance model under the condition of continuous time, based on Meton’s optimal investment-consumption model, which combined the method of replicating dynamic synthetic put option using risk-free and risk assets. And it transfers the problem of investor’s individual inter-temporal dynamic portfolio insurance decision into a problem of static utility maximization under condition of continuous time, and give the optimal capital combination strategies corresponding to the optimal wealth level of the portfolio insurers, and compares the difference of strategies between this model and Merton model. The conclusions show that investors’ optimal strategies of portfolio insurance are not dependent on their wealth, but market risk. That is to say, the higher the risk is, the more the demand of portfolio insurance is.

1. Introduction

In the past two decades, with the development of the globalization of international finance，there is the wave of financial innovation that financial institutions aid to avoid financial risks and improve their competitiveness. The early 80s of last century, a new hedging tool based financial derivatives—the portfolio insurance strategy— is very popular in the financial markets. Investors used this new type of hedging tools largely, and there were excessive trades, once a crisis, it may affect the entire financial system stability because of a series of events of default. There were two cases, one is the chain reaction of the collapse of Barings Bank in 1995, the other is the outbreak of the sub-prime crisis in 2007 that led to the global proliferation and amplification of financial risk, whose root cause is the credit risk of the excessive use of financial derivatives.

Earliestly, Rubinstein, etc. [1] put forward the concept of portfolio insurance, Grossman, etc. [2] gave a specific definition of that is a technology of hedging and shifting the risk using the financial derivative instruments such as options, futures or simulated options. The portfolio insurance developed very rapidly before the crash of stock market in 1987. At this stage, the appraisal of portfolio insurance was more affirmative, and the research focused on how to avoid the risk of stock market and how to utilize hedge. Literatures [1,3,4] proposed the model of portfolio insurance which is only deformation of optimal control model of Merton [5], and the ultimate goal of which is to control the end of the wealth of not less than a certain pre-set values. After the crashing of US stock market in October 1987, the attentions of scholars were affected by the problems that whether the implementation of portfolio insurance strategy would increase market volatility and how to use the portfolio insurance strategy effectively. The results of literatures [6-10] showed that the implementation of portfolio insurance using options do have influence on the market liquidity increase transaction costs, and then increase market volatility; the studies of literatures [11,12] showed that the increasing market volatility is not included by using of options to avoid risks, but by the uncertainty of the model itself; literature [13] researched the relations between portfolio insurance, benefits and risk of investors in high-risk market conditions; literatures [14,15] compared the different portfolio insurance strategies with different trading; literature [16,17] analyzed the problem of the minimum cost of portfolio insurance strategies, as well as the application of lattice theory in portfolio insurance; literature [18] analyzed portfolio insurance strategies under the transferring of the market volatility and structural changes; literature [19] studied the optimization of the CPPI strategy; literatures [20,21] proved the portfolio insurance is a stochastic dominance strategy with limitation using random process theory; literature [22] showed that portfolio insurance strategies contribute to the allocation of financial risks; literature [23] studied the CPPI strategy in the conditions of discrete-time.

The financial derivatives in China and relatively research are few lacking. Literature [24] showed the portfolio insurance strategy can be created by dynamical replicating futures options; literature [25] analyzed the portfolio insurance strategy by a empirical study of Monte Carlo, on; In literature [26] studied the problem of portfolio insurance using VaR-based futures markets; literature [27] analyzed not only the relations between the price volatility of risk asset and the value of portfolio insurance, but also between revenue and its cost, etc; literature [28] analyzed the dynamic insurance with the constraints of EaR.

Because of the long history of the development of foreign financial market, and more varieties of financial derivatives, the study on theory or empirical analysis of portfolio insurance focused on how to use portfolio insurance strategies to avoid risk and how to affect on the market volatility [1,29,30]. The financial market in China is just starting, derivative instruments is lacking, and options market does not exist currently, so the study also is limited to how to use the dynamic portfolio insurance strategies.

In this paper, we try to use stock and risk-free assets to replicate options to achieve the portfolio insurance, and establish a new dynamic model different from the existing model to analyze the implementation of the dynamic process of the strategy and the investors’ actions using dynamic replication strategy. Firstly, this paper established a dynamic portfolio insurance model in the conditions of continuous-time model by using the technology of dynamic replication options, which is not like the literature [1,3,4], which only added a lower limit in the final level of wealth; Secondly, the investor’s personal inter-phase dynamic portfolio insurance decision-making problem is changed into a static utility maximization problem; Finally, this paper achieves the best optimal portfolio strategy in the level of participants’ optimal asset, and compares similarities and differences between the optimal investment portfolio insurance model and the optimal investment strategy of the optimal investment and consumption model of Merton [5].

2. Model of Portfolio Insurance

In this paper, with the assumptions of principle of noarbitrage and a complete market, based on the model of optimal consumption and portfolio strategy in a continuous time of Merton [5], a model of dynamic portfolio insurance is created using dynamic replication of put option.

2.1. Complete Market Hypothesis

The complete market model assumes [29] under the condition of continuous-time is as follows.

1) Investors exist in a time period [0,T], T < ∞Investors will consume and invest in any (consecutive) time points, and insurance at time 0.

2) Uncertainty of Market is described by a complete probability space {Ω,Φ,P}. Information structure is generated by the Brownian motion on the definition of the above probability space, is

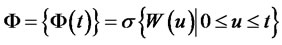
where.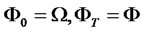

3) Suppose there are two financial assets in the marketone is a risk-free asset, 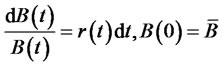, the other is risk asset, its price S(t) follow the Brownian motion.

.

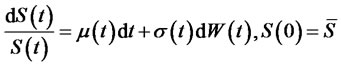where the risk-free interest rate r(t), expected rate of return of risk assets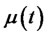; and the transient volatility is adapted to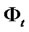and uniformly bounded in 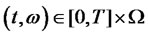; 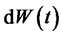is a standard Wiener process, the process of discounted price is.

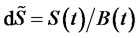4) The decision-making variables which investors control are two, one is the consumption for each moment, that is, the consumption process C(t), the other is the trading process or portfolio process 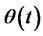(present the number of assets); the number of risk-free assets is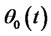, the number of risk assets is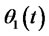, and is a predictable two-dimensional random variable, where

.

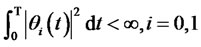5) The initial wealth of investor is

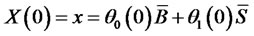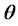. is the trading strategy with initial wealth, where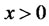, following by the process of wealth of investor.

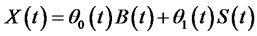where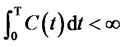, the process of wealth generated by the trading strategy and consumption is:

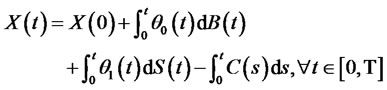(1)

The above formula demonstrates that the total wealth of the investor in the moment of t equals to the initial wealth plus payoff of risk assets and risk-free assets, and minus the total accumulating consumption. The proportions of investment in risk-free assets and risk assets are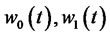, when the investment strategy is definited by using the relative proportion of the assets investing in the total personal wealth.

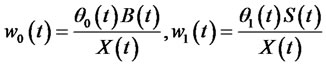(2)

where 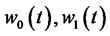is the portfolio process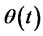, and

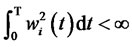, i = 0, 1. is a self-financing strategyaccording (1), the simple process of wealth is achieved:

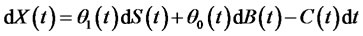(3)

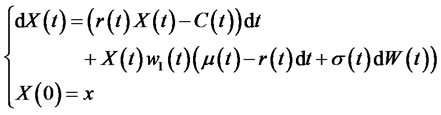(4)

Given a positive initial wealth x, a self-financing strategy 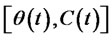or 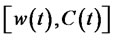produce a non-negative wealth process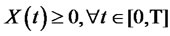, which is a admissible strategy. The entire set of feasible strategies 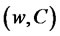based on x is denoted.

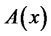6) The market price of risk in complete market 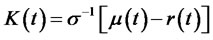has a unique solution which is bounded. There are Radon-Nikodym derivative

and the only measure of risk-neutral (martingale probability measure Q) according to Camron-Martin-Girsanov theorem [30], where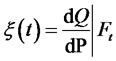, and the risk asset under the martingale probability measure Q is

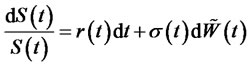(5)

after discounting, it becomes

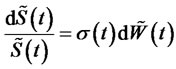(6)

then the price of risk asset 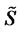turns into a martingale Q.

7) The state price density process

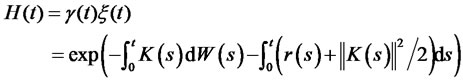(7)

is positive, continuous and progressively predictable, and is the unique solution of the following stochastic differential equation.

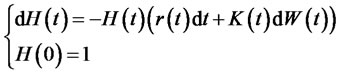(8)

where 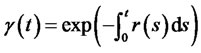is the discount factor.

8) There are all kinds of options matching with risk asset in the market.

Theorem 1. Given the initial wealth + and a admissible self-financing strategy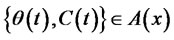, the corresponding process of wealth meets

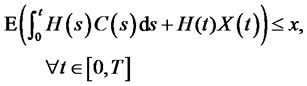
M is a non-negative random variable and adapted to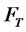, C(t) is a consumption process, 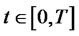,where

.

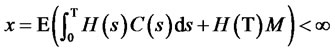So there is a portfolio process, where

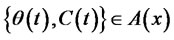, and the corresponding wealth process satisfies.

The proof of the theorem which can be found in literature [31] is similar to the process of optimal investment and consumption, and omitted.

2.2. Portfolio Insurance Market Model

The optimal model of portfolio insurance is expressed as to maximization of the total expected utility about consumption and the final wealth, that is,

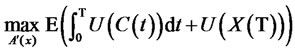(9)

Thus, an optimal strategy is solved.

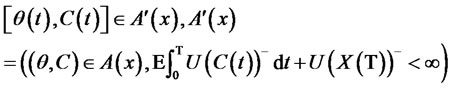
where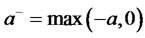, which demonstrates a weak and integrable condition.

The variables of dynamic trading strategies 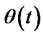include the number of risk-free assets, risk assets and the put option whose underlying is the risk assets with investing in portfolio insurance.

In order to simplify the process of analysis, we assume that the consumption 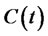during the period of investment is zero, and the variables of trading strategy controlled is. Because of dynamic replication strategy, the premium of options is zero. Based on these descriptions, portfolio insurance model is expressed as

(10)

According to (1), the process of wealth generated by the portfolio insurance trading strategy is

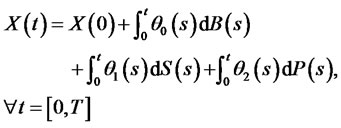(11)

Investors hold one risk asset and one put option P (the exercise price is K which is equal to the initial value of underlying assets), since they invest in portfolio insurance, then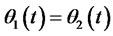, (11) becomes

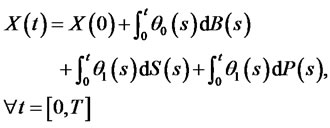(12)

That is the total wealth of investors at the time t equaling to the initial wealth plus the payoff of the investment in risk-free assets and risk assets as well as the put option. If 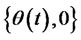is self-financing, the change of wealth are from the change of prices and the risk-free rate, the process of wealth is expressed as

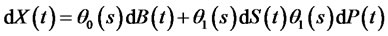(13)

Under the condition of no-arbitrage, we can replicate a put option by investing in the long position of risk assets

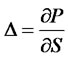and a short position of risk-free assets, then (13)

becomes

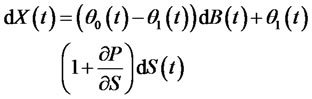(14)

ordering

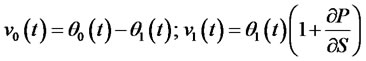(15)

then, (14) becomes

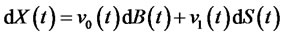(16)

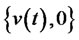is the set of investment strategy which includes ports of investing in risk-free assets and risk assets, according dynamic replication of options under the condition of no-arbitrary equilibrium. Comparing of (16) and (3), the model of portfolio insurance is similar to the general model of investment and consumption, because they have the same objective function which is maximizing the utility function of the wealth of investors. However the investment strategies 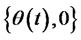which include investment in risk-free assets, risk assets as well as the put option, is changing into 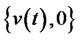which only include investment in risk-free assets and risk assets. So the model of portfolio insurance is

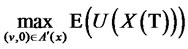(17)

where the process of wealth is (16). Similarly, according to Theorem 1, there is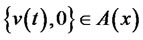, then.

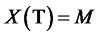The most important difference between our model and the models of literatures [1,4,5] is that the strategy include trading of portfolio insurance by using replicating technology,, rather than adding a restriction to the final level of wealth.

3. Optimization of Portfolio Insurance Model

In the continuous-time conditions, the optimization of portfolio insurance model includes two steps: the first step is that the decision-making problem of the investor’s personal inter-phase dynamic portfolio insurance is changed into a static utility maximization problem, then the optimal wealth level of the investor; the second step is that the corresponding optimal strategy is obtained with martingale representation theorem.

3.1. Deformation of Model

Portfolio insurance model (17) is similar to the investment-consumption model in micro-finance, and the investment strategy is changed from 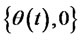of the investment-consumption model into 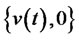of the portfolio insurance model. Then

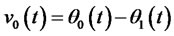
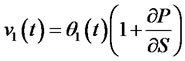
According to optimization theory, we definite

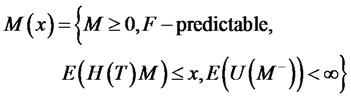
is predictable.

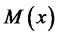is the set of all final wealth which is generated by a feasible trading strategy with the initial wealth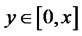, and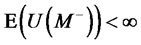. To optimize the model of portfolio insurance (17) and get the optimal final wealth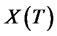, we can maximize all the random variables of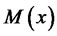, which is achieved with the martingale probability measure Q :

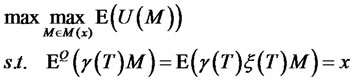(18)

As a result, the portfolio insurance model (17) becomes the static optimization of model (18).

3.2. Optimization of Model

If 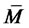is the optimal solution to the equation (18), 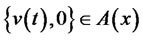with has to be achieved. To find a trading strategy with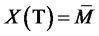, we construct the Lagrange function:

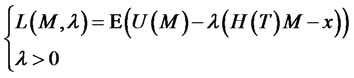(19)

We calculate derivatives of 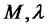in equation (19).

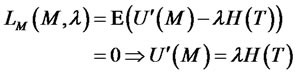(20)

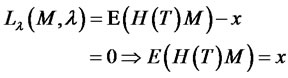(21)

Because the utility function is monotonic decreasing strictly, there is an inverse function 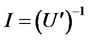which makes the optimal level of final wealth is

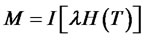(22)

To substitute equation (22) into (21).

(23)

Ordering

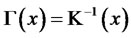(24)

According to equation (22), the optimal solution is

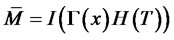(25)

Because of

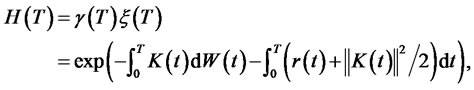
the optimal solution is

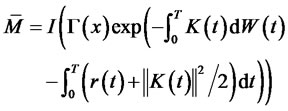
Theorem 2. In the optimization of equation (17), if

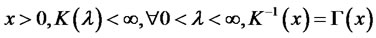, to the optimal final wealth

.

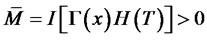There is a self-financing portfolio process 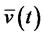and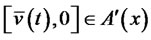, which is the optimal solution of equation (18).

Theorem 2 and Theorem 1 is similar, the proof is omitted. Superscript 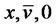demonstrates the initial wealth, the investment strategy and consumption. To simplify the model, the consumption process is always 0.

3.3. Analysis of the Optimal Portfolio Insurance Strategy

To find the solution of optimal portfolio insurance strategy, from (2) the value of risk-free assets and risk assets which the investors invest in portfolio insurance is

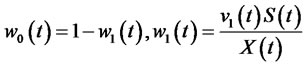(26)

where 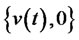is the investment strategy set investing in risk-free assets and risk assets using dynamic replicating options method under no-arbitrage equilibrium analysis. As the wealth process of the self-financing portfolio process 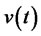is expressed as the formula (4), using the state price function, there is

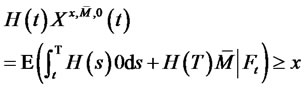(27)

The integral 0 indicated the consumption process, that is the consumption is 0.t The optimal portfolio process is.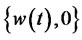

Using Ito’s theorem, there is

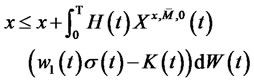(28)

As the investor participates in insurance, the smallest earning of investor in the end is x, the formula (28) is

so

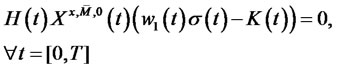(29)

Because 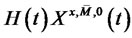is always positive, so

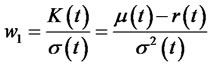(30)

After dynamic replicating option, we can obtain the investment strategy set of the model (18). And the investment strategy set 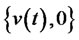investing in risk-free assets and risk assets is

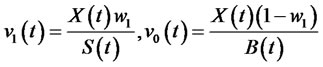(31)

Formula (30) is the same to the result of literatures [5, 31]. After investing in portfolio insurance, if we obtain the solution of the model of portfolio insurance using the way of dynamic replication options, the investor’s proportion of investing the risk assets is similar with the result of the optimal investment consumption model (where the consumption is 0).

Because 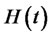is the solution of

and satisfies the formula (27), the process of consumption 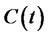is always 0,

(32)

is the process of wealth accompanied by the optimal trading strategy.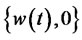

Comparing with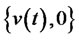, we can obtain the trading strategy 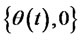of the portfolio insurance problem (10) which includes investments in risk-free assets, risk assets as well as options underlying risk assets.

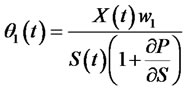(33)

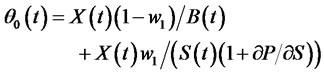(34)

Comparing (33), (34) with (31), there are similarities and differences between the optimal portfolio insurance model and the optimum investment strategy of the optimum investment consumption model.

Firstly, the former set of optimal strategies is divided into three parts: investment in risk-free assets, risk assets and options; the latter is divided into the two parts: investments in risk-free assets and risk assets.

Secondly, the share of investment in risk-free assets 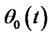in the optimal investment strategy of the portfolio insurance model includes two parts. One is the investment in risk-free assets without insurance (the first part of the right of formula (34)), the other is the investment in risk-free assets which replicates options with insurance (the latter part of the right of formula (34)). The sum of both is less than the share of investment in risk-free assets of the optimal investment and consumption model. The share of investment in risk assets is more than that of the optimal investment and consumption model by comparing the denominator of formula (33) whit that of formula (26), which the denominator of 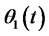is smaller than of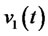. Because is always less than 1, which is the same to the result of replicating one option by investing in the long of risk assets 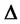and the short of risk-free assets in the analysis of no-arbitrage equilibrium. To implement the portfolio insurance strategy, That is, in order to the investor must invest more 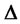in the risk assets for risk assets.

Finally, if the risk-free interest rate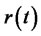, the expected return rate of risk assets 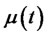and the instantaneous volatility rate 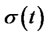are constant, the trading strategy 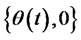of portfolio insurance model (10) after putting the formula (33) and (34) into the formula is

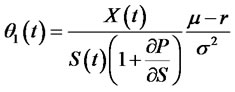(35)

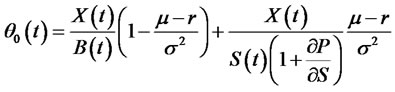(36)

Therefore, to achieve the positive initial wealth x, the investor of portfolio insurance investing in risk assets and options are both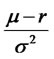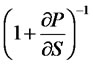. And it is independent of the level of wealth, which is decided by the risk premium (the ratio of the difference between the average return rate of risk assets and the return rate of risk-free assets to volatility rate) and the amount of investing in risk assets to replicate portfolio insurance strategy.

4. Conclusions

The portfolio insurance model of this paper is similar to the investment consumption model which has the same function, and is the maximization of the investor’ utility function. The only difference is that the other models have a restriction of the final wealth. This paper shows the portfolio insurance strategy by replicating put option with risk-free assets and risk assets in the entire investment process, so we may clearly analyze the dynamic behavior of investors.

Through the analysis of the optimization of dynamic portfolio insurance model, we find that the share of investment in risk-free assets of the optimal investment strategy is less than the share in the general model. However, the share of investment in risk-free asset is more than the share in the general model, because the option is copied by the long position of risk assets and the short position of 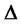risk-free in the strategy of dynamic investment portfolio insurance. That is investors must have more risk assets to insure.

The proportion investing in risk assets and options of portfolio insurance which is determined by the risk premium and 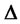is independent of the level of wealth. It indicates the demand of investors for insurance is independent of the wealth, but dependent on the market risk. In the other words, the higher of the market risk, the greater the demand for portfolio insurance. The conclusions of this paper reflect the function of avoiding the risk of the portfolio insurance strategy.

The implementation of portfolio insurance strategy is a complicated systems engineering. It is used to avoid and manage the risk of market, and faces the potential risks because of the special character of the strategy itself. Based on dynamic portfolio insurance model and its optimal strategy, the study of this paper is a basis for the further research of the portfolio insurance in China and give some conclusions that provides a reference for the theoretical research and practical investment operations of financial market. Meanwhile, it also is a theoretical foundation for China’s development of financial derivatives market and provides some technical supports for the investors to avoid market risk using the portfolio insurance strategy.

REFERENCES

NOTES

^*Project supported by the National Natural Science Foundation of China (No. 71101045), by Foundation for University Key Teacher by Henan Province (No. 2010GGJS-031), by Programs Foundation for Scientific Innovation Talent Henan Province (No. 2009HASTIT017).