Journal of Mathematical Finance
Vol.2 No.1(2012), Article ID:17588,3 pages DOI:10.4236/jmf.2012.21004
On the Insignificant Cross-Sectional Risk-Return Relationship
Nanyang Business School, Nanyang Technological University, Singapore City, Singapore
Email: *zfli@ntu.edu.sg
Received November 21, 2011; revised January 16, 2012; accepted January 25, 2012
Keywords: CAPM; Portfolio Theory; Mathematical Finance; Market Risk and Expected Return; Cross-sectional Relationship; Theory and Evidence; Mathematical Derivation
ABSTRACT
In their paper, “On the Cross-sectional Relation between Expected Returns and Betas”, Roll and Ross (1994) demonstrated that the expected returns and betas can have zero relationship even when the underlying market portfolio proxies are nearby the efficient frontier. In this note, we provide the mathematical details that lead to their conclusion and further show that their claim needs not hold for the entire set of MV portfolios.
1. Introduction
There is ample empirical evidence that sample mean returns and estimated betas have no statistically significant relationship. For example, Fama and French (1992) [1] finds no cross-sectional beta-return relation after controlling for firm size and book-to-market financial ratio.
Roll and Ross (1994) [2] demonstrate that expected returns and betas can have a zero relationship even if the underlying market portfolio proxies are nearby the efficient frontier, whereas the relationship can always be positive if generalized least square (GLS) regression is used for the test. Their demonstration implies an extreme sensitivity of the empirical test of cross-sectional relationship to the choice of proxies for market portfolio.
In this paper, we provide analytical details on the crosssectional relationship examined in [2]. Our derivation clarifies the sensitivity of the risk-return covariability to the choice of index proxies and thus characterizes the index proxies that lead to the insignificant relationship.
2. Derivation of the Index Proxies
For comparability, let’s employ the notations used in [2]. Let R denote the vector of expected returns for the N individual assets. Let V be the N ´ N covariance matrix of returns. The unit vector is denoted by 1, the portfolio weights vector is denoted by q, and the scalar expected portfolio return is r = q'R.
The scalar portfolio return variance is σ2 = q'Vq and the cross-sectional or time series variance of asset j is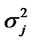 . The cross-sectional mean or expected returns is denoted by
. The cross-sectional mean or expected returns is denoted by 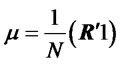 and
and 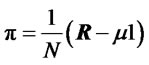 is the vector of scalar expected return deviations from the crosssectional mean. The scalar slope from cross-sectional regressing R on betas computed for individual assets against portfolio q is denoted by k.
is the vector of scalar expected return deviations from the crosssectional mean. The scalar slope from cross-sectional regressing R on betas computed for individual assets against portfolio q is denoted by k.
Note that the slope coefficient estimate (the sample beta) of a time-series regression Rit = αi + βi Rmt + eit, is given by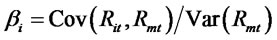 , where
, where
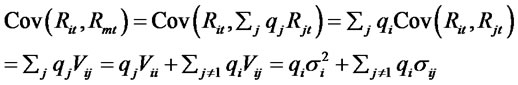
since  and
and  .
.
Denote β as the vector of the slope coefficient estimates. Then we must have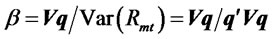 . In order to see this, consider the covariance of each individual stock and the portfolio,
. In order to see this, consider the covariance of each individual stock and the portfolio,
 (1)
(1)
Since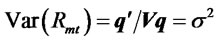 , it follows from (1) that
, it follows from (1) that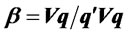 .
.
A minimum variance (MV) index proxy should satisfies the following three conditions: 1) the portfolio’s expected return is a fixed value, r; 2) its weights q sum to unity; and 3) a cross-sectional regression of expected returns R on betas ( )) has a given slope k. The MV index portfolio can be obtained from minimizing
)) has a given slope k. The MV index portfolio can be obtained from minimizing 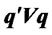 with respect to q, subject to
with respect to q, subject to
 , (2)
, (2)
 , and (3)
, and (3)
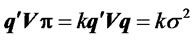 . (4)
. (4)
The main characteristic of the MV index portfolio is implied in the third constraint (equation (4)). Consider a cross-sectional regression
 .
.
The slope is given by , where,
, where,
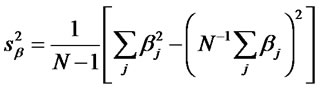 .
.
Since k = Cov(R, β) and
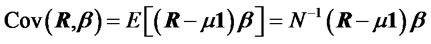 we know that
we know that
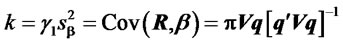 .
.
Because the variance is treated as a simple constant, the β stationarity is implicitly assumed.
Note that the Lagrange function is given by

Hence, the first order conditions for a minimum are
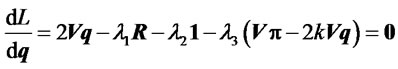 , (5)
, (5)
together with three constraints that collectively satisfy
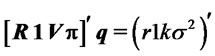 (6)
(6)
Thus in Roll and Ross (1994) the market portfolio weights are given by
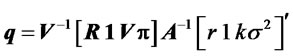 , (7)
, (7)
where  is a 3 ´ 3 matrix.
is a 3 ´ 3 matrix.
3. Detailed Derivation of the Market Portfolio Weights
Based on equation (7), Roll and Ross (1994) claimed the sensitivity of the risk-return covariability to the choice of index proxies. Hence in order to understand their claim, we need to examine the details behind the mathematical derivation of equation (7).
The first order condition (5) can be written as

Pre-multiplication of the above equation by V–1 leads to
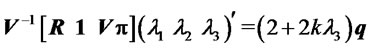 (8)
(8)
In order to obtain a solution for the Lagrange multipliers λ, we pre-multiply equation (8) by 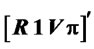 to obtain
to obtain
 (9)
(9)
We need to eliminate λ3 from the right hand side of equation (8). By the substitution of equation (9) into (8), equation (8) becomes
 (10)
(10)
The substitution of equation (6) into (10) yields the following desired solution
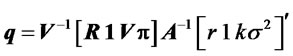 provided that 2 + 2kλ3 ¹ 0.
provided that 2 + 2kλ3 ¹ 0.
In order to see that 2 + 2kλ3 ¹ 0, suppose the contrary, that is, 2 + 2kλ3 is indeed zero. Then, λ3 must be −1/k. However, if λ3 = −1/k, then it follows from equation (9) that λ1 = λ2 = λ3 = 0, which contradicts the premise that λ3 = −1/k.
4. Conclusion
Roll and Ross (1994) [2] the expected MV portfolio return and its variance are both treated as constants. Hence, the implicitly-assumed beta stationarity implies k is also constant. The choice of index proxies (in terms of explaining the cross-sectional return-risk relationship) is an increasing function of k. It also follows that the return of the market portfolio q'R is also an increasing function of k. Hence, our exposition in this note shows that the claim of Roll and Ross (1994) need not hold for the entire set of MV portfolios.
5. Acknowledgements
The authors have received valuable comments from Andrew Chen, Yonggan Zhao, Charlie Chareonwong and participants of the CREFS Seminar at the Nanyang Business School, Nanyang Technological University, Singapore.
REFERENCES
- E. F. Fama and K. R. French, “The Cross-Section of Expected Stock Returns,” Journal of Finance, Vol. 47, No. 2, 1992, pp. 427-466. doi:10.2307/2329112
- R. Roll and S. A. Ross, “On the Cross-Sectional Relation between Expected Returns and Betas,” Journal of Finance, Vol. 49, No. 1, 1994, pp. 101-121. doi:10.2307/2329137
NOTES
*Corresponding author.

