Received 6 August 2013; revised 16 February 2014; accepted 4 March 2014

ABSTRACT

In recent years, numerous researches have been carried out with purpose of predicting motor vehicle crashes on transportation facilities as freeways and urban or rural highways. Accident process can be modeled successfully with assuming a dual-state data-generating process. Based on this assumption, road components like intersections or road segments have two states of perfectly safe and unsafe. Zero-inflated regression models are applied to model accidents usually in cases of preponderance of excess zero data in crash data. We handle in this research, the investigation into effective factors on frequency and severity of accidents on urban highways and use crash data of Mash had-Iran urban highways as a case study. We use in this study, the Poisson, Negative binomial, Zero-inflated Poisson and Zero-inflated Negative binomial regression models for modeling accidents, and traffic flow and road geometry related variables as in dependent variables of models. In addition to identifying effective factors on crash occurrence probability, we deal with comparison of models, evaluate and prove the efficiency of Zero-inflated regression models against traditional Poisson and Negative binomial models.

Keywords:

Accidents; Modeling; Urban Highways; Traffic Flow; Zero-Inflated Regression Models

1. Introduction

In recent years, numerous researches have been carried out with purpose of predicting motor vehicle crashes on transportation facilities as freeways and urban or rural highways [1] -[6] . The range of statistical models commonly applied includes binomial, Poisson, negative binomial, zero-inflated Poisson and negative binomial models (ZIP and ZINB), and multinomial probability models. Given the range of possible modeling approaches, making an intelligent choice for modeling motor vehicle crash data is difficult. There is little discussion in the literature comparing different statistical modeling approaches, identifying which statistical models are most appropriate for modeling crash data, and providing a strong justification from basic crash principles. Motor vehicle crash process can successfully be modeled by assuming a dual-state data-generating process, which implies that entities (e.g., intersections, road segments, pedestrian crossings, etc.) exist in one of two states―perfectly safe and unsafe. The ZIP and ZINB are two models that have been applied to account for the preponderance of excess zeros frequently observed in crash count data [7] .

In this paper, we deal with research that have been conducted for identifying the effective factors on frequency and severity of accidents on urban highways and use crash data of Mashhad urban highways as a case study. These data were gathered by transportation and traffic organization of Mashhad, using GIS for accurate record of time and place of accidents and assistance of police reports. The traffic flow and road geometry related factors have been used in this research as independent variables of models. Such variables are observed in studies of many other researchers particularly in the area of modeling crashes occurred on freeways and urban or rural highways [8] -[13] . Some researchers also applied pavement condition or quality [14] [15] , driver behavior [10] [13] [14] [16] and weather condition [13] [14] related variables as independent variables in their models. In this research, traffic volume and speed are applied as traffic flow related variables. In previous researches, the average daily traffic (ADT) or annual average daily traffic (AADT) was applied in modeling as traffic flow related variable [12] [17] or to consider number of lanes in each side, ADT or AADT per lane was used [8] [9] [11] . The special attempt made in this research, was the separation of traffic volume into vehicle groups volume including passenger car, heavy vehicle and light non-passenger car vehicle volumes, light non-passenger car vehicles consists of taxi, pickup and motorcycle. The purpose of this attempt was to study thoroughly the role of each vehicle group of traffic flow, in occurrence and severity of crashes. Other Investigators were used in modeling variables such as average daily truck traffic (ADTT) or percentage of trucks to account for the role of heavy vehicles in frequency and severity of highway accidents [9] [11] [15] or variables of average daily passenger car traffic and average daily truck traffic or percentage of trucks separately for detachment of the role of passenger cars and heavy vehicles in accident occurrence [15] . The other volume-related variable is traffic speed. Although this factor may be considered naturally as an effective item in accident process, it should see firstly, whether or not this factor has also in practice, considerable part in accident process. Secondly, this factor contributes more to accident occurrence or severity. In this study and some other studies [12] the value of traffic speed in each segment of highway is used for modeling crashes, however in many previous studies the posted speed limit in different segments of highways is considered as independent variable [8] [11] [13] .

Factors applied as road geometry related variables in this research, include number of lanes, horizontal curves and access roads. Although in some investigations, the factors of ADT or AADT per lane were applied in modeling instead of ADT or AADT, for considering the variable of number of lanes [8] [9] , such variables are seen in many past researches [12] [15] [17] . Using variables of number of horizontal and vertical curves in specified distances of highways as road geometry related variables, is observed in many researches [8] [11] [15] , however the average degree of curvature of horizontal curves [9] [15] , gradient or length of vertical curves [8] [9] in each segment of highway have been applied in modeling in some studies. Access roads are roads which enter or exit the highway and interfere the traffic flow. Some researchers applied variables of number of interchanges [9] , at-grade intersections [8] or ramps [15] in specified distances of freeways or highways, instead of number of access roads.

Statistical models applied in this research to identify effective parameters on crash occurrence on urban highways are four well-known regression models in crash modeling―Poisson, Negative Binomial (NB), Zero- Inflated Poisson (ZIP) and Zero-Inflated Negative Binomial (ZINB). Regression models in this research are developed for modeling accidents with property loss only and more severe accidents included injury and fatal accidents. After developing models, based on modeling conclusions, we examine the part of independent variables in probability of occurrence of accidents with property loss only and more severe accidents. Then we evaluate the models “goodness of fit” and compare them to find out the best and fittest models for no injury (with property loss only) and more severe (injury or fatal) accidents on urban highways.

2. Methodology

In this research, the accidents of urban highways of Mashhad are modeled by four regression models―Poisson, Negative binomial (NB), Zero-inflated Poisson (ZIP) and Zero-inflated Negative binomial (ZINB). Two groups model were developed, one for accidents with property damage only and the other for more severe accidents (injury or fatal). Independent variables applied in these models include traffic-related and geometry-related variables. Flow-related variables include traffic volume and speed and geometry-related variables include number of lanes, horizontal curves and access roads. The specific effort made in this research, in addition to development and analysis of four considerable statistical models separately for modeling accidents, is separation of total traffic volume into passenger car volume, heavy vehicle volume including truck trailer, truck, bus and minibus and light non-passenger car vehicle volume including taxi, pickup and motorcycle. By this attempt, we intend to have a thorough look into the role of volume in occurrence of accidents with property damage and injury or fatal ones and see exactly which part of traffic have an effective or more effective part in accident occurrence. What is often heard is the role of heavy vehicles in crash occurrence, but it should be found out whether heavy vehicles result in more accidents or passenger cars or light non-passenger car vehicles like taxis or motorcycles have key role in accident occurrence or frequency.

Accident data are usually two-level data, the first and main level is often road segments i.e. the highway is divided into several parts or segments. The base of this segmentation is different, segmentation can be based on segment length that is, division of highway into equal segments. The problem of such division is that one can not assign to each section a constant value for traffic volume, which is considered an important and effective factor in this study. It is preferred therefore to do this segmentation based on total traffic volume. The second level is daily hours that is, the traffic peak hours is considered as the first sub-level, the day non-peak hours the second and night non-peak hours the third one.

The SAS 9.1 was used for statistical computations related to models. After statistical analyses, it is found out which parameters affect accident occurrence and which does not have much part in accident occurrence. The other important care in this research is evaluating models and their comparison to examine the efficiency of zero-inflated (ZI) models against traditional Poisson and Negative binomial (NB) regression models in modeling property and injury or fatal accidents on urban highways. In this study, to compare Poisson and NB regression models and also ZIP with ZINB regression models, we use significance of dispersion parameter and likelihood ratio (LR) test as criterions. The statistic of likelihood ratio test is given by the following equation:

(1)

This statistic has a Chi-squared distribution with degrees of freedom, in which 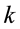is number of regression coefficients. If the statistic is greater than the value of 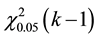then, the model2 is better than the 1. The consequence of this test for comparing models mentioned is usually equivalent to evaluating the dispersion parameter. Vuong statistic is also used for comparison between Poisson model and ZIP. But this is one stage of comparison; the other stage is goodness-of-fit evaluation of models and their fit comparison. To do this, Akaike Information Criteria (AIC) or Bayesian Information Criteria (BIC) is applied. AIC and BIC are calculated as:

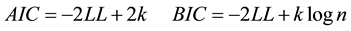(2)

where LL is log-likelihood, k number of parameters and n number of observations. The less AIC is, the more model fit and model with the least AIC is the fit test one [18] . Consequences of model evaluation by AIC and BIC are similar and their values are close together. Results of the second stage of comparison often approve the first stage conclusion.

2.1. Poisson Regression Model

In Poisson regression model, the i-th observation of dependent variable 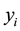is modeled as a random Poisson variable with mean:

(3)

In Poisson model, the conditional variance is equal to conditional mean:

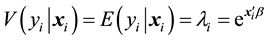(4)

The log-likelihood of Poisson regression model is given by:

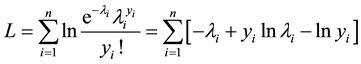(5)

For estimating the regression coefficients by maximum likelihood method, derivative of log-likelihood relative to vector of coefficients, 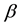is set equal to zero:

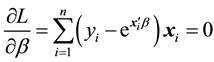(6)

Estimation of regression coefficients in Poisson regression model is not obtained of a direct equation, but the Newton-Raphson iteration procedure is used for estimating unknown parameters of the model [19] . To do the estimation process, the corresponding iteration algorithm is given to SAS statistical software to obtain the calculated coefficients.

2.2. Negative Binomial Regression Model

In negative binomial (NB) model, the i-th observation of dependent variable has the following probability distribution function:

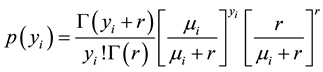(7)

The conditional mean of, for the vector of observed independent variables, 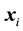is given by:

(8)

The cause of investigators’ inclination for NB distribution is disadvantage of Poisson distribution in equality of mean and variance of distribution. The relationship between mean and variance of NB distribution is as following:

(9)

The variance of NB distribution is always greater than the mean, thus it fits the data with variance greater than mean. is dispersion parameter. For accident data with low dispersion, use of Poisson distribution for modeling gives plausible results but if over dispersion exists in data, variance of data will be greater than the mean, in such cases NB distribution is preferred.

In NB regression model, dispersion parameter should be estimated in addition to regression parameters. is restricted to be positive, so is estimated instead, which can take on any value. The log-likelihood of NB model is obtained from following equation:

(10)

For estimating and, as in Poisson model, the iteration procedure of Newton-Raphson is applied [8] [20] . To do so, the related iteration algorithm is written in SAS to obtain unknown parameters.

2.3. Zero-Inflated Regression Models

The other problem, which accident data often encounter, is preponderance of excess zero data. In other words, number of zero data is more than expected in Poisson and NB models. If one meets with excess zero data while data mining, uses zero-inflated (ZI) distribution for data analysis.

The underlying assumption of ZI models is that entities (e.g., intersections, segments, crosswalks, etc.) exist in two states [21] :

1. True-zero or inherently safe state. Although in recent years some have defined it as “virtually safe state” to avoid having to defend the notion that sites can be perfectly safe

2. Non-zero state, which may happen to record zero accidents in an observation period that follows the Poisson (ZIP) or NB (ZINB) distribution.

First state happens with probability and the second.

Accident data are usually two-level data that the first level is often a specific segment of road and the other could be a specific period of year or hours of day. If number of crashes occurred on the i-th section in the -th period, follows a ZIP distribution, the probability mass function is as following:

(11)

In ZIP model, the mean of Poisson distribution, is linked to a regression of independent variables, by logarithm link function and the probability of zero process, to a regression of independent variables, by log it link function:

(12)

where and are vectors of regression coefficients.

If accident data suffer from over dispersion in addition to excess zero data, as in NB regression model, ZINB regression model is applied in modeling. A count variable with ZINB distribution has probability mass function as following [8] [22] :

(13)

ZIP and ZINB regression models are in fact a combination of Poisson and NB models with a model which models zero data. Therefore, the log-likelihood function, which is set to estimate the regression coefficients β and,should consider both models. For non-zero data, the log-likelihood function is the one for Poisson or NB models and for zero data, this function is defined as:

(14)

where is the value of Poisson or NB probability function in zero.

Usually for simplicity of estimation, the same variables of vector are considered for vector. As a result, the link relationships of distribution mean, and, the probability of the process which generates zero data only, will be as following [18] :

(15)

For testing the relevance of using ZI models instead of Poisson and NB regression models, the Vuong statistic is used. If, j = 1, 2 is the probability of, number of accidents and:

(16)

where and are probability mass functions of ZI and Poisson or NB models respectively, Vuong statistic is obtained by following equation [23] -[25] :

(17)

where is mean, standard deviation and sample size.

Vuong statistic is asymptotically standard normally distributed, and if is less than 1.96 i.e. the 95% confidence level for the t-test, the test does not have any results. However, the zero-inflated regression model is favored if the value is greater than 1.96, while value of less than −1.96 favors the Poisson or negative binomial regression model [23] . This test unlike the likelihood ratio test, which is used to compare Poisson and NB models, is not a numerical test in which the result is obtained by comparing the negative two times log likelihood of two models, but according to Equations (17) and (18), one encounters an iteration process that iterates for each observation and the value of probability function of Poisson and ZIP models for that observation. Thus for corresponding computations, SAS should be applied [18] .

3. Data

The accident data of Mashhad-Iran urban highways were used for modeling accidents on urban highways. This information is collected by Transportation and Traffic Organization of Mashhad with the help of GIS and using Police reports. In this research two groups model are applied to number of accidents with property loss only (no injury) and more severe accidents (injury or fatal). Therefore accident statistics were collected in two groups of no injury and more severe. Accident data are usually two-level data, the first and main level is often road segment i.e. highway is divided into several parts. In this study, highway segmentation is performed based on total traffic volume. The second level is daily hours that is, traffic peak hours is considered as the first sub-level, the day non-peak hours the second and night non-peak hours the third sub-level. The traffic flow related variables including volume and speed and geometric variables including number of lanes, horizontal curves and access roads, are applied as independent variables of models in this investigation.

To scrutinize the part of different vehicle types in crash occurrence or severity, the traffic is separated into passenger cars, heavy vehicles and light non-passenger car vehicles. The volume data separately were not available readily in Transportation and Traffic Organization of Mashhad. The Organization conducts once every few years, a comprehensive survey in November and obtains the passing volume of different kinds of vehicles through a main part of urban roads in daily hours. In November, the traffic condition of Mashhad is normal and basically, models made in this research do not consider the seasonal changes of traffic, because the statistics of traffic volume in different seasons were not available and the volume data is related to different hours of the day. According to this statistics, one can perceive the traffic combination and percent of each vehicle type in traffic and can trust this combination in future, but the total (equivalent) traffic volume is updated every year.

The Transportation and Traffic Organization of Mashhad, gives out the total traffic volume on different urban roads particularly highways in peak hours, for future years. According to this total equivalent volume, with having passenger car equivalent factors of vehicle types, percent of each in traffic combination and the ratio of total volume in non-peak hours to that in peak hours, the volume of each vehicle type in peak hour and 2 hours representing day and night non-peak hours will be obtained and also the volume of passenger cars and equivalent volume of heavy vehicles and light non-passenger car vehicles in peak hour and 2 representative hours of non-peak day and night hours. These calculations are conducted by Excel program. The passenger car equivalent factors of vehicle types are given in Table 1 [26] .

The total volume (passenger car equivalent) is obtained by following equation:

(18)

where V_te is the total equivalent volume and and are equivalent factor and number of vehicles type i respectively.

As the numbers of vehicle types are counted hourly, these numbers are volumes in terms of vehicle per hour. The speed data in different parts of highways for peak hours and non-peak day and night hours are collected by Traffic Organization. The data related to number of lanes, access roads and horizontal curves in dif- ferent segments are collected from the highways route map with the help of Google Earth. The summary sta-

tistics of the crashes and independent variables of the models, from 2006 to 2009 for 156 sections of Mashhad urban highways, with 67.5 kilometers length in overall, in 1872 sub-sections (468 sub-sections, considering 3 daily periods, for each year) are presented in Table 2. The total numbers of no injury and more severe accidents occurred on all sections of urban highways of Mashhad from 2006 to 2009 are 13,071 and 1776 respectively.

4. Statistical Modeling

We intend to explore in this investigation, the effective factors on frequency and severity of crashes on urban highways through modeling no injury and more severe (injury and fatal) accidents on urban highways. The well known models of Poisson, Negative binomial (NB), Zero-inflated Poisson (ZIP) and Zero-inflated Negative binomial (ZINB) are applied to developing two groups model for no injury and more severe accidents. Here, according to collected statistics of accidents and data related to independent variables, the models are developed.

4.1. Poisson Regression Model

For estimating regression coefficients by maximum likelihood approach, Equation (6) is used. For estimating unknown parameters of the model, the iteration method of Newton-Raphson is applied. We consider first a vector of regression parameters as primary estimate, and obtain the second parameter estimate from iteration relation (19) and so on until the difference between two successive estimates becomes less than tolerance level. The estimate before the last is the desired estimated coefficients. The iteration relation is as following:

(19)

where is the gradient evaluated at, the first partial derivative of the log likelihood in called gradient and is the hessiane valuated at, the second partial derivative of log likelihood is called hessian, as following:

(20)

For evaluating significance of independent variables, the inverse hessian obtained at the last iteration will be the asymptotic variance matrix. The variance of the estimates are the diagonal elements and the standard errors their square roots. The t statistic for each parameter is also constructed as the ratio of the parameter estimate over its standard error. If the p-value of a parameter is less than needed level of significance (0.05 or less), the corresponding variable is significant and will stay in model, otherwise it is neglected and leaves the model [19] .

Such calculations were proceeding by SAS, estimated parameters and their significance evaluation for accidents with property loss only and more severe accidents are presented in Table 3.

4.2. Negative Binomial Regression Model

For estimating regression coefficients and dispersion parameter, the Newton-Raphson iteration procedure is applied like Poisson model, but the process is more complicated. First of all, we put or Poisson regression then the regression parameters is estimated by following iteration:

(21)

where. Then is estimated by iteration as:

(22)

where. Now and estimated regressors are applied as initial estimate θ in

the following iteration to estimating updated values of and:

(23)

where:

(24)

The estimated values of and in the iteration before the last, is what we look for. is the inverse dispersion parameter [20] . The significance evaluation of independent variables of NB regression model is similar to Poisson model. The estimated parameters of model and their significance evaluation for property and more severe accidents are presented in Table 3.

4.3. Zero-Inflated Regression Models

In ZI regression models, the link relations of distribution mean, and, the probability of process which generates only zero data are presented in equation. Significance evaluation of regression coefficients is as before, except that significant variables of link relation is different from that for and usually number of significant variables of (ZI) part is less than that for (Poisson or NB) part. Also for examining the appropriation of using ZI models instead of Poisson or NB models, the Vuong test is applied. The estimated parameters of models and their significance evaluation for no injury and injury or fatal accidents are presented in Table 4.

4.4. Models Evaluation and Comparison

What is considerable after modeling, is not only significant variables issue but goodness-of-fit evaluation and comparison between models i.e. not only after modeling we will see which variables have considerable effect on likelihood of property and more severe accidents but model fit and comparison issue is also considered. After receiving results, first Poisson and NB models are compared in terms of data dispersion, so the significance evaluation of dispersion parameter in NB model and LR test is implemented. For comparing Poisson and ZIP models, Vuong test is applied and comparison between ZIP and ZINB models is also made by significance evaluation of dispersion parameter and LR test, note that the result of comparison between Poisson and NB models could not be extended to ZI models. The other step of comparison is goodness-of-fit evaluation of models and their fit comparison, so Akaike (AIC) or Bayesian (BIC) information criteria are employed. The results of comparison in the second stage often approve the first. The results of goodness-of-fit evaluation of models and their comparison are presented in Table 5.

5. Results and Discussion

After developing models for crashes with property damage only and more severe crashes (injury and fatal), we handle analyzing results and discussion and also evaluation and comparison between models to see which variables play considerable roles in crash occurrence on urban highways and which do not have much parts in it. After that, we handle evaluation and comparison between models and will see which models fit better for modeling the likelihood of no injury and more severe accidents.

The results of developing four regression models of P, NB, ZIP and ZINB including regression parameters and significance of independent variables for both no injury and more severe accidents are presented in Table 6.

The increase in likelihood of accidents with number of access roads, as is clear from results and reflected in Table 6, was not unexpected because access roads in segments of urban highways interfere the highway flow and this could increase the probability of crash occurrence with increase in number of conflicts. The accidents could be with property loss only or more severe.

As the results show, the probability of accident occurrence increases with number of horizontal curves, either property accidents or more severe ones. This result has a consistency with some researches [17] , but is incompatible with some others [9] [11] . For instance, Chang (2005) concluded in his study on accident frequency on freeways that the existence of horizontal curves greater than six degree in freeway sections reduces accident likelihood. He justified it as; drivers are more likely to drive cautiously at horizontal curves [9] . Also Milton et al. (2008) conclude in their investigation that the number of horizontal curves per mile significantly reduces the

^*Highlighted Coefficients are significant at 5%.

likelihood of injury accidents for all highway segments. Their explanation for this were, as the curve density increases, individuals may adjust by driving more slowly to provide more time to process information and to increase their ability to safely negotiate the curves [11] . But as naturally expected, the existence of curve in segments of urban highways increase the likelihood of accidents on those segments, the present researchers believe that at least on Iran’s urban highways, one could not count much on decrease in accident likelihood on sections with horizontal curve as a result of more cautiously driving.

The results of modeling crashes presented in Table 6 indicate that, number of lanes increases the likelihood of accidents with property damage only, but does not have any effect on more severe accidents. The result is consistent with previous findings [9] [12] , although when the number of lanes increases the traffic flow gets more convenient, the traffic conflicts and driving maneuvers such as lane changing increase and consequently the probability of accident occurrence.

The results show that, speed of traffic plays an effective role on occurrence of accidents with property damage, as the likelihood of property accidents increases with speed, but it does not have much impact on occurrence of injury or fatal accidents. Some researchers implemented the posted speed limit or exceed or not the speed limit as independent variable in modeling crashes and found out that exceeding the speed limit increases the likelihood of injury accidents [8] [13] . This finding is not consistent with our results, an explanation for this that, studies of other researchers is more often on rural or urban highways with high speed limits but our research is conducted on urban highways with lower speed limits. The increase in speed, lessen the driver’ dominance on vehicle and increase the number of conflicts and consequently probability of accident occurrence, but what result in accidents with more severity are high speeds which is usual in rural highways. In urban highways of Iran, because of existing defects in geometric design of highways and higher V/C than normal, maneuvering and speeding possibility on urban highways is less than that in countries in which corresponding researches is carried out, therefore except for dangerous driving behavior of young drivers in high speeds, the speed could not be considered as an effective factor on accidents severity on urban highways of Iran.

The results of investigation show that the volume of passenger cars and light non-passenger car vehicles have an increasing impact on likelihood of no injury (with property damage only) accidents, but the volume of heavy vehicles does not have much effect on no injury accidents. Also, the volume of light (non-passenger car) vehicles increases the likelihood of injury or fatal accidents, but the volume of passenger cars and heavy vehicles do not have much impact on likelihood of injury or fatal crashes. Researchers came up with different results; Chang (2005) concluded in his studies that conflicts between vehicles and probability of accident occurrence increase with number of vehicles and trucks. First part of this conclusion is consistence with our findings but the other is not [9] . Also Milton et al. (2008) found out in their studies, taking into consideration the random effects for independent variables, that for 75.2% of the roadway segments, an increasing number of trucks decreases the likelihood of accidents resulting in injury and for remaining 24.8%, an increasing number of trucks increases the likelihood of accidents resulting in injury [11] , which is not consistent with our findings.

After analyzing the results of modeling, we handle goodness-of-fit evaluation and comparison between models. For accidents with property loss, as is clear from Table 5 the dispersion parameter is significant in NB model and the negative value of two times log likelihood is much greater for Poisson model than NB model and the value of LR statistic is, which is much greater than equal to 14.07. Therefore it is concluded that NB regression model is better than Poisson model for no injury accidents. But for comparison between Poisson and ZIP model, the Vuong statistic is implemented. According to Table 5, the statistic is equal to 10.6, greater than 1.96, so ZIP model is better than Poisson. Note that Vuong test is in fact performed for evaluating the significance of ZI models. The significance of dispersion parameter in ZINB model and that the negative value of two times log likelihood is sufficiently greater for ZIP model than ZINB, indicate that ZINB is better than ZIP model. The second stage of comparison is comparing model fit, according to Table 5, the comparison of AIC value between four models demonstrates that ZINB regression model with the lowest value of AIC is the best and fittest model for no injury accidents.

For more severe accidents, as is clear from Table 5, dispersion parameter is significant and LR statistic is equal to, which indicates that NB is better than Poisson model. The Vuong statistic is also equal to 3.83, greater than 1.96 which points that ZIP model is better than Poisson. But as the dispersion parameter of ZINB model is significant and LR statistic is, greater than, ZINB model is better than ZIP. Eventually, As the AIC value for ZINB model is less than other models; it is evident that this model is the best and fittest model for modeling injury or fatal accidents on urban highways.

6. Summary and Conclusions

In this research, we dealt with investigation into effective factors on frequency and severity of accidents on urban highways. The statistical methodology applied in this research, is employing four well known regression models in modeling highway accidents comprising Poisson, Negative binomial, Zero-inflated Poisson and Zero-inflated Negative binomial regression models. In this study, the accident data of Mashhad-Iran urban highways were used as a case study, traffic flow and road geometry related variables as independent variables of models were used to scrutinize the part of traffic in accident occurrence and severity, the traffic volume was divided into volumes of passenger cars, heavy vehicles and light non-passenger car vehicles.

In conducted research, we developed two groups model one for accidents with property damage only (no injury) and one for more severe accidents (injury or fatal) and concluded that, the likelihoods of no injury and more severe accidents increase with existence and number of horizontal curves and access roads, also as speed and number of lanes increase, the likelihood of no injury accidents increases but it does not have much effect on likelihood of more severe accidents. The results of research indicate that, the volume of passenger cars and light (non-passenger car) vehicles have increasing impact on likelihood of no injury accidents, but the volume of heavy vehicles does not have much effect on probability of occurrence of no injury accidents. Also, the volume of light vehicles increases the likelihood of injury or fatal accidents, but the volume of passenger cars and heavy vehicles does not affect much likelihood of such accidents. After that, we handled goodness-of-fit evaluation and comparison between models and concluded that, zero-inflated negative binomial regression model is the best and fittest model, both for no injury and more severe accidents.

References

NOTES

^*Corresponding author.