Journal of Quantum Information Science
Vol.06 No.01(2016), Article ID:64831,8 pages
10.4236/jqis.2016.61004
Modified BB84 Protocol Using CCD Technology
Subhashree Basu1, Supriyo Sengupta2*
1Department of Computer Science and Engineering, St. Thomas College of Engineering and Technology, Kolkata, India
2Department of Electronics and Communication Engineering, St. Thomas College of Engineering and Technology, Kolkata, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 October 2015; accepted 17 March 2016; published 22 March 2016
ABSTRACT
Quantum cryptography and especially quantum key distribution (QKD) is a technique that allocates secure keys only for a short distance. QKD protocols establish secure key by consent of both the sender and receiver. However, communication has to take place via an authenticate channel. Without this channel, QKD is vulnerable to man-in-the-middle attack. While not completely secure, it offers huge advantages over traditional methods by the use of entanglement swapping and quantum teleportation. In our research, we adopt the principle of charge-coupled device (CCD) to transfer the qubit from the sender to the receiver via a quantum channel. This technology has an added advantage over polarizer as only the circuit for transmitting the qubit is sufficient. No extra circuitry to implement the polarizer is required.
Keywords:
Quantum Cryptography, Quantum Key Distribution (QKD), Entanglement, Teleportation, Charge-Coupled Device (CCD)

1. Introduction
Cryptography is the design and analysis of mathematical techniques that enable secure communications in the presence of malicious adversaries. It is a science of protecting information by encoding it into an unreadable format. Cryptography has immense applications in the field of broadcast and network communication, such as electronic transactions, the internet, e-mail, and cell phones, where sensitive monetary, business, political, and personal communications are transmitted over public channels.
A sender scrambles or encrypts the original message in a systematic way that obscures its meaning. The sender transmits the encrypted message, and the receiver recovers the message by unscrambling or decrypting the transmission.
Public Key Cryptography (PKC) uses a pair of mutually inverse transformations: one to scramble the information and the other to unscramble the information. Then the scrambling transformation is published. PKC systems exploit the fact that certain mathematical operations are easy to compute in the forward direction but cannot be computed in the reverse by classical computers [1] [2] . However, recent work in quantum computation [3] [4] suggests that a quantum computer might be able to compute such complex computations in practical times, which could jeopardize the authenticity of many modern cryptography algorithms. But quantum technology can also ensure secure communication at an even more fundamental level.
Quantum cryptography [5] - [9] can be used to ensure the confidentiality of information transmitted between two parties by exploiting the counter-intuitive behavior of particles such as qubits. In quantum computing, a qubit or quantum bit (sometimes qbit) is the basic unit of quantum information. It can be considered as the quantum analogue to the classical bit. In a classical system, a bit would have to be in either state 0 or 1. However, quantum mechanics allows the qubit to be in a superposition of both the states, and this is a fundamental property of quantum computing which makes it so different from the classical world. Hence the qubit can be represented as a linear combination of 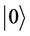 and
and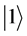 .
.
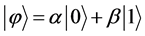 (1)
(1)
where 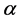 and
and 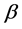 are probability amplitudes and can be complex numbers. When measured in the standard basis, the probability of outcome
are probability amplitudes and can be complex numbers. When measured in the standard basis, the probability of outcome 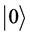 is
is 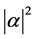 and the probability of outcome
and the probability of outcome 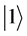 is
is 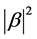 where
where
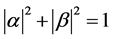 (2)
(2)
Quantum Key Distribution [10] - [18] is a state-of-the-art technique that exploits properties of quantum mechanics to guarantee the secure exchange of secret keys. The crypto systems developed so far use polarized light photons to transfer data between two points. Each photon therefore carries one bit of quantum information, which is called as a qubit. To receive such a qubit, the recipient must determine the photon’s polarization, which has to be done by passing it through a polarization filter. This will inevitably alter the photon’s properties. Thus any intervention of an eavesdropper can easily be recognized by the alterations introduced to the measurements.
In this paper, the first attempt is made to use electric charge and electric fields instead of light and polarizer to generate the qubits. This can be realized by using charge-coupled device. The BB84 QKD protocol [19] has been modified to incorporate the above approach.
2. Related Topics
2.1. Charge-Coupled Device
A CCD [20] [21] is an electrical device that is commonly used to create images of objects, store information, or transfer electrical charge. It receives an electrical charge as an input. It then transfers the charge via potential wells―the output. The electronic signal is then processed by some other equipment and/or software to either produce an image or to give the user valuable information. The storing function comes from shifting these charges, simultaneously, down a row of cells, in discrete time. Also, an analog signal can be delayed a discrete time for synchronization purposes. It has an immense application in image sensors. The packets of charge are not initially converted to an electrical signal, but rather moved from cell to cell by the coupling and decoupling of potential wells within the semiconductor that make up the CCD. At the end of the line the charges, can be converted to electrical signals.
Each cell of a CCD contains a metal oxide semiconductor (MOS). CCDs are typically fabricated on a p-type substrate. The “buried” channel is implemented by creating a thin n-type region on its surface. An insulator, in the form of a silicon dioxide layer is grown on top of the n-region. The capacitor is finished off by placing one or more electrodes, also called gates, on top of the insulating silicon dioxide. These electrodes could be metal, but more likely a heavily doped polycrystalline silicon conducting layer would be used [19] .
CCD can be built by placing a number of such single cells arranged in a single row. At one end, called the input, we send the initial charge electro statically which at the other end, called the output, is converted back to an electric signal. If all goes well, the output electric signal is a reasonable copy of the input electric signal, but it is sampled at discrete points in time. Control wires are used to control the height of the various potential wells. The changing well height is what pushes and pulls the charge packets along the line of CCDs. The diagrammatic representation of a CCD is shown in Figure 1.
2.2. Quantum Bit Error Rate of Quantum Channel
The Quantum Bit Error Rate (QBER) [19] is the measurement of the probability of error in the key distribution across the quantum channel. It is one of the key quantities in quantum communications which is used to characterize the quality of signal transmission in QKD systems. It can be affected by several factors, such as type of the protocol used, transmission impairments to the quantum bits, noise and imperfections of the components in the link. The QBER is the ratio of an error rate to the key rate and contains information on the existence of an eavesdropper and how much such eavesdropper knows. This value allows the users to estimate the maximum amount of information that an eavesdropper could have on the key.
In simple terms, the QBER can be calculated as:
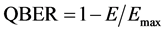 (3)
(3)
where:
E is the number of correctly transmitted bits,
Emax is the total number of transmitted bits.
This definition of the QBER contains an implicit assumption that without eavesdropping QBER is equal to zero. Obviously, the QBER for an ideal quantum channel without noise is equal to zero and can use the QBER to estimate Eve’s interference. Hence for simulation purposes, the maximum error rate of 40% has been chosen as the upper bound.
2.3. BB84 Protocol
The operation of BB84 QKD protocol is described below. It comprises of two main stages:
Quantum Channel (one way communication) Classical Channel (two way communication)
In the first stage, Alice and Bob set up a quantum channel to distribute the key. During the second stage, they recover the final key using the classical channel.
Alice and Bob are equipped with two polarizer each, one aligned with the rectilinear 0˚ or 90˚ (or +) basis that will emit − or | polarized photons and one aligned with the diagonal 45˚ or 135˚ (or ×) basis that will emit \ or / polarized photons. Alice and Bob communicate via the quantum channel to send photons. Later they discuss the
Figure 1. Diagrammatic representation of a complete CCD.
polarization of the photons over the classical channel and finally decide the key.
In this method, Alice can send the qubit via any of the two quantum paths at the sender end. The propagation of information in the form of qubits takes place following the principle of CCD. Four phases θ1, θ2, θ3, θ4 are arbitrarily selected by Alice. These phases are selected randomly but to avoid predictability, the phases should not be selected such that θ1= (−θ2) = (π − θ1) and so on.
Now Alice assigns two phases to one path and the other two phases to the other path in a random basis. The basic principle of this approach is that when a sender sends a key in the form of a qubit, that qubit can choose any of the two paths based on the electric fields applied to the paths. The path that the qubits will choose can be decided by Alice by adjusting the height of the potential wells in the CCD. Similarly the phase shifts can be implemented by introducing a certain amount of delay in the path equivalent to the angle of phase shift. The moment the qubits pass through the phase shifts, the state of the qubit should change hence the actual data gets manipulated. At Bob’s end, again two paths with two different combinations of phases are applied. Hence, the incoming qubit again can pass through any of the channels and will be subjected to two phase shifts at the receiving end.
In order to get back the actual qubit, the receiver has to apply the opposite phases to that of the sender. For example, if the phase shift θ1 and θ2 are applied at the Alice’s end, then (π − θ1) and (π − θ2) phase shift should be applied at the Bob’s end in order to get back the original qubit. One thing that has to be kept in mind is that this whole setup should be in the quantum channel where no intervention with the classical world can take place.
As shown previously, a qubit can be represented as
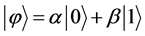 (4)
(4)
When Alice introduces a phase shift of θ1 then the state of the qubit in Equation (4) can be represented as
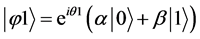 (5)
(5)
Again, applying the phase shift of θ2 to the state in Equation (5) gives
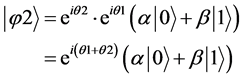 (6)
(6)
And this qubit is propagated to the receiver. At the receiver’s end, If Bob is able to guess the value of phase shifts correctly, then after applying the two phase shifts at the receiver’s end, the state of the qubit in Equation (6) becomes

Hence applying complementary phase shifts to that of the sender’s end at the receiver’s end, we should get back the actual qubit. The diagrammatical representation of how the system can be implemented is shown in the Figure 2 below.
Let us now consider an example. Alice begins to send qubits to Bob, each one phase shifted at random by two of the four angles whose sequences are also selected at random for example: 13˚, 45˚, 110˚, 205˚. As Bob receives each qubit, the qubit will pass through any one of the quantum path at the receiver’s end. Since Bob does not know which angles Alice chose for her phase shifts, his choice may not match hers. If it does match the basis, Bob will measure the same qubit value as Alice sent, but if it doesn’t match, Bob’s measurement will be completely random. For an example, if Alice sends a qubit and the phase shift applied is 13˚ and 45˚ and Bob measures with his phase shift 167˚ and 135˚, he will correctly deduce the value of qubit that Alice sent, but if the measures with any other phase shifts, he will deduce wrong values of the qubit. Furthermore, his measurement will have destroyed the original qubit.
Table 1 shows how the bit string is recovered in the proposed method. In this particular example, Alice chooses random bit string (row 1) and phase shift them using the random angles given in row 2. Row 3 shows
Table 1.Key Recovery in proposed method.
Figure 2. Diagrammatic representation of the proposed mothod.
the phase shifted bit string that travel to Bob’s end. Bob in turn uses random phase angles (row 5) to obtain a key string which comprises of errors. After sending all the qubits in the key, Alice and Bob begin a public discussion via a classical channel. There is no need for Alice and Bob to discuss the actual state of the qubits sent. Bob tells Alice which phase shifts he used to measure each qubits, and Alice tells him whether it was the correct one or not. They discard all data for which their phase angles did not match. After this stage, Alice and Bob produce a shorter sequence of bits which are known as Raw Keys. The aim of this phase is to agree on the correct phase angles used by both parties.
If there is no intrusion, then Alice’s and Bob’s raw keys will be in total agreement. However, if there is an intrusion by an eavesdropper Eve, these raw key are subject to errors. During the eavesdropping, Eve tries to gain information about the key by intercepting the qubits as they are transmitted from Alice to Bob, measuring their phase angles, and then resending them so Bob does receive a message. Since Eve, like Bob, has no idea which basis Alice uses to transmit each qubits, she too chooses the phase angles at random for her measurements. If she chooses the correct basis, and then sends Bob a qubit matching the one she measures, the raw keys will be in total agreement. However, if she chooses the wrong basis, she will propagate wrong sequence to Bob and the raw keys will not match.
Thus Alice and Bob have to estimate the errors introduced by Eve’s eavesdropping as well as by other means. Thus, to estimate the errors, Alice and Bob choose a subset of their raw keys and publicly compare the bits to calculate the bit error rate (R) of the recovered key. If the calculated R is less than the threshold error rate (i.e. QBER) for the quantum transmission, Alice and Bob can safely assume that the errors introduced are acceptable to proceed with. Then they remove the bits revealed from their raw keys .If the calculated R is greater than the threshold error rate for the quantum transmission, the errors introduced are beyond the acceptable limit and it is impossible for them to arrive at a common secret key. Hence they abort the rest of the process and initiate a new quantum transmission.
The steps that follow are similar to that of the BB84 algorithm [19] .
3. Result Analysis
The QBER can be calculated for the above method and the key obtained can be accepted or discarded based on the calculated QBER. The main advantage of the method is that it is practically implementable. It does not use photons in order to represent the qubits like most of the previous QKD protocols. Hence this removes the problem of separating a single photon from a packet of photons which is a problem in practical. Moreover we do not need any polarizer. Here we are using an already existing technology of CCD which is the basic technology used in MEMS and is very much practically implementable. The phase shifts can be implemented by only controlling the height of the potential wells and by controlling the time delay for which a qubit resides in a well. No extra circuit is required as compared to the implementation of the polarizer where extra wires or plates will be required to implement the polarizer.
QKD protocols implemented by photons can be breached by laser beam incident on the photon detector at the receiver’s end which will render the receiver’s photon detector ineffective. Receiver’s detector can no longer detect and distinguish between different quantum states of incoming light. However, it still works as a classical detector, and can record bit values of 1 or 0 regardless of the quantum properties of the pulse. So, eavesdropper can intercept the bit and can resend a pulse to receiver so that he also receives a correct signal and is completely unaware that his detector has been sabotaged. This has been possible because at whatever polarization the photon is being oriented, they are interpreted as 0 or 1.
But, in our proposed method, we are dealing with the quantum state of the qubits and are not concerned about their classical state. So, whatever state, the qubit is at the sender’s end, it can never come as 0 or 1 at the receiver’s end. Only after the receiver applies the two phase shifts, the qubit can take the state of 0 or 1. Moreover, incidenting a laser at the receiver’s end will certainly change the qubit but will not disable the CCD. So, the receiver will be able to measure the qubit, even if it is the wrong magnitude. So, even if the setup is breached and an eavesdropper reads the qubit and sends a classical bit instead, the receiver will immediately realize that an interception has taken place.
Whether the degree of noise in the qubit stream is acceptable or not can be calculated by the QBER. In order to make the whole setup full proof, we can enclose the setup within a quantum conduit, so that no external fields can affect the setup. In this context we have to keep in mind that this method does not ensure reduction in the number of resources as compared to that of using polarizer. But the advantage is we can insert a phase shift of any value using CCD whereas polarizer can have only two orientations (45˚ or 135˚) and (90˚ or 180˚). Obviously, decryption becomes more tedious in our proposed method as compared to that of using polarizer.
4. Conclusion
Quantum technologies will play a pivotal role in the future as it has been proved that quantum computers will have massive computational power because it can do computational tasks in parallel and can solve problems whose solutions are virtually unthinkable in conventional computers. Such system can also provide more security for information sharing. The proposed method gives such a protocol for information security, which can be implemented in real time applications as it is designed using an already existing technology of CCD.
Cite this paper
SubhashreeBasu,SupriyoSengupta, (2016) Modified BB84 Protocol Using CCD Technology. Journal of Quantum Information Science,06,31-38. doi: 10.4236/jqis.2016.61004
References
- 1. Moore, T. and Ballentine, K. (2012) Serpent Cipher Design and Analysis. A Report, Rochester University of Technology, Rochester.
- 2. Daemen, J. and Rijmen, V. (1999) AES Proposal: Rijndael. A Report, NIST, the Computer Security Resource Center (CSRC).
- 3. Mattle, K., Weinfurter, H., Kwiat, P.G. and Zeilinger, A. (1996) Dense Coding in Experimental Quantum Communication. Physical Review Letters, 76, 4656-4659.
- 4. Das, R., Mahesh, T.S. and Kumar, A. (2002) Implementation of Conditional Phase-Shift Gate for Quantum Information Processing by NMR, Using Transition-Selective Pulses. Journal of Magnetic Resonance, 159, 46-54.
http://dx.doi.org/10.1016/S1090-7807(02)00009-5 - 5. Nguyen, T.M.T., Sfaxi, M.A. and Ghernaouti-Hélie, S. (2006) 802.11i Encryption Key Distribution Using Quantum Cryptography. Journal of Networks, 1, no. 5,
- 6. Paterson, K.G., Piper, F. and Schack, R. (2007) Quantum Cryptography: A Practical Information Security Perspective. In: Zukowski, M., Kilin, S. and Kowalik, J., Eds., Quantum Communication and Security, Proceedings, NATO Advanced Research Workshop, IOS Press, Amsterdam, 175-180
- 7. Cederlöf, J. and Larsson, J.-Å. (2008) Security Aspects of the Authentication Used in Quantum Cryptography. IEEE Transactions on Information Theory, 54, 1735-1741.
http://dx.doi.org/10.1109/TIT.2008.917697 - 8. Bakhtiari, M. and Maarof, M.A. (2011) An Efficient Stream Cipher Algorithm for Data Encryption. International Journal of Computer Science Issues, 8, 247-253.
- 9. Sharma, R.D. (2011) Quantum Cryptography: A New Approach to Information Security. International Journal of Power System Operation and Energy Management (IJPSOEM), 1, 11-13.
- 10. Kulkarni, D.H. (2012) Research Directions in Quantum Cryptography and Quantum Key Distribution. International Journal of Scientific and Research Publications, 2, 1-3.
- 11. Reddy, I.S., Reddy, K.S., Reddy, M.P., Bhat, P.J. and Rajeev (2012) Key Distillation Process on Quantum Cryptography Protocols in Network Security. International Journal of Advanced Research in Computer Science and Software Engineering, 2, 19-24.
- 12. Tsurumaru, T. and Hayashi, M. (2013) Dual Universality of Hash Functions and Its Applications to Quantum Cryptography. IEEE Transactions on Information Theory, 59, 4700-4717.
http://dx.doi.org/10.1109/TIT.2013.2250576 - 13. Godhavari, T. and Alamelu, N.R. (2013) Quantum Encoder and Decoder for Secret Key Distribution with Check Bits. Research Journal of Applied Sciences, Engineering and Technology, 6, 4381-4386.
- 14. Luo, W.J. and Liu, G.L. (2014) Asymmetrical Quantum Encryption Protocol Based on Quantum Search Algorithm. Journal of China Communications, 11, 104-111.
- 15. Kilor, P.P. and Soni, P.D. (2014) Quantum Cryptography: Realizing next Generation Information Security. International Journal of Application or Innovation in Engineering & Management (IJAIEM), 3, 286-289.
- 16. Elliott, C. (2004) Quantum Cryptography. IEEE Security & Privacy, 2, 57-61.
http://dx.doi.org/10.1109/MSP.2004.54 - 17. LaMonica, M. (2013) Long-Distance Quantum Cryptography. IEEE Spectrum, 50, 12-13.
- 18. Hughes, R.J., Alde, D.M., Dyer, P., Luther, G.G., Morgan, G.L. and Schauer, M. (1995) Quantum Cryptography. LA-UR-95-806.
http://arxiv.org/abs/quant-ph/9504002 - 19. Wijesekera, S. (2011) Quantum Cryptography for Secure Communication in IEEE 802.11 Wireless Networks. PhD Thesis, University of Canberra, Bruce.
- 20. Peterson, C. (2000) How It Works: The Charged-Coupled Device, or CCD. The Journal of Young Investigators, 3.
- 21. Felber, P. (2002) Charge-Coupled Devices: A Literature Study. Illinois Institute of Technology, Chicago.
NOTES
*Corresponding author.





