Journal of Quantum Information Science
Vol.05 No.03(2015), Article ID:60004,4 pages
10.4236/jqis.2015.53013
The Lines of Lyman and the Titus-Bode Law Preferred Orbital of a Celestial Body
Raoul Charreton
Diplomé Ecole Nationale Supérieure des Mines de Paris, Paris, France
Email: raoul.charreton@mines-paris.org
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 September 2015; accepted 25 September 2015; published 28 September 2015
ABSTRACT
We have proposed, thanks to a new model of the hydrogen atom [1] , some explanation of the lines observed by Lyman in the spectrographic analysis of this atom. The model is based on a pre- quantum physics, itself founded on classical mechanics completed by the existence of a universal cloud of tiny particles called U. This cloud induces simultaneously and similarly electromagnetic and gravitational effects. This common origin creates a narrow link between how planets are arranged in a solar system, say the Titus-Bode law, and how the electrons are arranged in an atom, say the lines of Lyman. We describe what this link is in the following text and, more generally, what is the preferred orbit of an isolated celestial body.
Keywords:
Planets, Lyman, Titus-Bode

1. The Lines of Lyman
The electron of an hydrogen atom is a charged particle surrounded by a train of k particles U from the universal cloud. The number k oscillates, say between k and k + 1 at each shock of a U particle on the electron and its moving average value is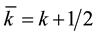 , a semi-integer number. At long intervals, because of an exceptional shock by its energy, very large or quite small,
, a semi-integer number. At long intervals, because of an exceptional shock by its energy, very large or quite small, 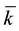 increases or decreases by 1. Yet, if the atom is in its fundamental state,
increases or decreases by 1. Yet, if the atom is in its fundamental state, 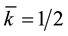 , k oscillates between 0 and 1 and cannot decrease by an exceptional shock. Each train commands the mass m of the electron, i.e. its internal energy w = m・c2 in natural units.
, k oscillates between 0 and 1 and cannot decrease by an exceptional shock. Each train commands the mass m of the electron, i.e. its internal energy w = m・c2 in natural units.
Natural units: We retain natural units of time, length and mass so that Planck constant h = 1 and not h = 2π, so that the speed of light in the universal cloud of particles be 1, and so that the average inertial mass of an isolated electron, with an average nil speed versus the universal cloud, be m = 1.
The value of these units in the International System is the following:
・ Natural unit of time h/(m∙c2) = 8.1 E−21 second.
・ Natural unit of length h/(m∙c) = 2.4 E−12 meter.
・ Natural unit of mass m = 9.1 E−31 kilogram.
・ Natural unit of energy m∙c2 = 8.2 E−14 Joule.
The principal quantum number of the electron is n = 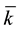 + 1/2, hence respectively
+ 1/2, hence respectively 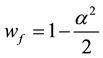 and
and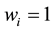 ,
,
the energy of the electron in the fundamental state and in the ionized state, α designating the fine structure constant. The identified energies by the lines of Lyman according to the prime positive number n are
 , n finite and
, n finite and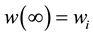 . (The line of the ionized state being said to have a wavelength of 911.267 Angstrom.) According to Bohr’s model, one associates to each value of the quantum number n a radial distance
. (The line of the ionized state being said to have a wavelength of 911.267 Angstrom.) According to Bohr’s model, one associates to each value of the quantum number n a radial distance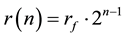 ,
, 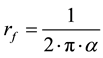 designating the radial distance in the fundamental state, called Bohr radius.
designating the radial distance in the fundamental state, called Bohr radius.
According to our model of pre-quantum atomic physics, the train of electrons in the ionized state of the atom is made of a finite number no of particles U, with an order of magnitude of 100.
Let ru be the reach of electromagnetic influences. According to the teaching of today, this reach is not limited. According to pre-quantum physics, it would be limited by the free course of U particles of the universal cloud between two shocks among them. This free course, noted ru is certainly large. If the universal cloud is locally populated by hydrogen atoms, ionized or not, with a sufficient volumetric density, then the U particles have shocks with the composing neutrons and electrons from time to time and their free course between smaller than ru. Strictosensu, an isolated hydrogen atom does not exist and an orbit of electron around the proton at a distance of the order of magnitude ru has no physical reality.
We retain ru ≈ a galactic radius, i.e. 45,000 light years. This range ru governs the value of no.
 , then
, then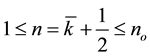 , then
, then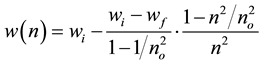 ,
, 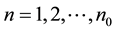 ,
,
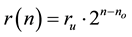 ,.
,.
This model is compatible with the observations.
2. Titus-Bode Law
One seeks to compare the distances of the various planets to the Sun. Each distance is well-defined if the orbit is circular. If not, we keep the semi latus rectum as the estimate of this distance.
Nota: An ellipse is defined in polar coordinates r and θ by , L being the semi latus rectum, e the eccentricity. The semi-major axis is
, L being the semi latus rectum, e the eccentricity. The semi-major axis is
Be i the rank of a planet according to the measured increasing distances ranking order. Planets are ordered by their distances to the sun: Mercury of rank 1, Venus, Earth, Mars, Ceres, Jupiter, Saturn, Uranus, Neptune of rank 9, and the Titus-Bode law puts a distance r to the Sun according to their rank i. Be AU the astronomical
unit of distance, i.e. the distance from the Earth to the Sun, For Mercury of rank i = 1,

well verified (by ≈3%) except for Neptune.
3. Stable Distances According to Pre-Quantum Physics
Pre-quantum physics reveals Lyman lines as preferred energies of the electron of a hydrogen atom, i.e. an electron in the vicinity of a proton with both particles in the universal cloud of U particles. Each preferred energy corresponds to a number 
Let us consider the Sun or a star as a tight gathering of hydrogen atoms and a test body such as an isolated hydrogen atom. One admits a priori that the orbit of a planet is little function of its mass and therefore that the orbit of the test body can be the image of a planetary orbit.
The gravitational effect of a star made of 



In the same way as one distinguishes 2 extreme states for the hydrogen atom―the fundamental state in which w and r are noted wf and rf, the ionized state with w and r noted wi and ri―one distinguishes two extreme states for the couple made by the star and test body, the gravific fundamental state with W and R noted as Wf and Rf, and the state without gravific influence, called “ionized” by extension, with W and R noted as Wi and Ri.
The direct computation of the W and R characters thanks to the pre-quantum model is possible but it can be made more easily by transposing the already computed electromagnetic effects because the gravific and electromagnetic effects are produced similarly in the pre-quantum model.
Here is the transposition of r towards R, the radii of the preferred planetary orbits which we search for in order to compare them with the observable radii in the solar system
The transposition is made by substituting 2∙π∙G∙m1∙m2 to α and m2 to m, m1 designating the mass of the celestial body, m2 that of the test body, m that of the electron, and G the Newton constant of attraction law.
Reminder: m2 = Wi/c2 and m1 ≈ M∙Wi/c2. In natural units c = 1, m2 ≈ Wi∙m1 = M∙Wi. Then 


Ru = ru, the reach of the gravific influence is the same as that of the electromagnetic influence. It is a finite distance.
N is the number of U particles of the test body, a hydrogen atom, according to the considered’ system gravific state, N0 this number in the state without attraction, N = 1 this number in the fundamental gravific state.

One does not expect to find R(1) of the order of magnitude of the distance from the Sun to Mercury when one takes for M an estimate of the number of hydrogen atoms of the Sun because the planets on orbits such as R be smaller than the apparent radius of Sun, or even smaller than ten times this radius, are subject to diverse non gravific but widely larger effects.
One can compute all preferred R distances but it is wise not to compare observations other than those which are farther than a ≈ 10 solar radii, and at less than b ≈ twice the distance from Sun to Pluto. The upper limit is the threshold above which the influence of Sun becomes smaller than the gravific influence of the galaxy, the considered model being no more acceptable as that of an isolated celestial body with a test body. R(N) is established as the model of the isolated system of a celestial body and a body test, not a celestial body such as Sun, and a test body, in the galaxy.
Numerical values are the following ones in natural units:
Mass of the proton mp = 1836;
Mass of the electron = 1;
Mass of the hydrogen atom m2 = wi = mp + 1 − σ2/2 ≈ 1837;
Mass of Sun mS = 2.18 E60;
The dimensionless number MS = mS/m2 ~ 1.2 E57;
The G constant of Newton’s law in natural units, G = 2.8 E−46;
Radius Rf of the test body or satellite in the fundamental gravific state of the couple Sun-satellite, Rf = 1.23 E−23;
Common reach ru and Ru of electromagnetic and gravific influences, ru = Ru ≈ galactic radius, i.e. 45 000 light years, i.e. 1.7 E32 natural units of h/(m∙c) length;
Number N0 of U particles in the train of hydrogen atom in its limit gravific state, N0 = 184.
Nota: It is easy to check that the obtained values of R(N) on the a to b support little depend of the Ru retained value, and therefore of N0, as soon as Ru is large enough.
Be A(j), j = 1, 2, ..., N the satellite of rank j of the isolated system of a celestial body A and of a satellite in the universal cloud.
Be P(i), i = 1, 2, ..., 9 the solar planet of i index, 1 for Mercure, 9 for Pluto.
Be R(j) the distance between the celestial body A to the A(j) satellite of circular orbit.
Be SLR(i) the semi latus rectum of the solar orbit of Planet P(i).
Be ji(i) the rank of P(i) defined by lSLR(i) - R(ji(i))l = minimum lSLR(i) - R(j)l, j = 1, 2, ..., N.
One presents the list of A(j), R(j) and of P(ji(i)), SLR(ji(j)) in increasing numbers of R(j) and under the condition a < R(j) < b with a ≈ 10 solar radii, b ≈ twice the distance from Sun to Pluto.
Satellite of rank 149, R = 0.07 AU;
Satellite of rank 150, R = 0.14 AU;
Satellite of rank 151, R = 0.28 AU;
Planet Mercury with the same 151 rank, SLR = 0.37 AU;
Satellite of rank 152, R = 0.57 AU;
Planet Venus with the same 152 rank, SLR = 0.72 AU;
Satellite of rank 153, R = 1.1 AU;
Planet Earth with the same 153 rank, SLR = 1. AU;
Planet Mars with the same 153 rank, SLR = 1.5 AU;
Satellite of rank 154, R = 2.3 AU;
Planet Ceres with the same 154 rank, SLR = 2.7 AU;
Satellite of rank 155, R = 4.6 AU;
Planet Jupiter with the same 155 rank, SLR = 5.2 AU;
Satellite of rank 156, R = 9.1 AU;
Planet Saturn with the same 156 rank, SLR = 9.5 AU;
Satellite of rank 157, R = 18. AU;
Planet Uranus with the same 157 rank, SLR = 19 AU;
Satellite of rank 158, R = 37. AU;
Planet Neptune with the same 158 rank, SLR = 37 AU;
Satellite of rank 159, R = 73. AU;
Remark 1: On the ato b support, the number 11 of preferred distances and the number 9 are close to each other. In itself, this is a rather astounding result.
Remark 2: The R(N) distances do not coincide with the radii SLR(i) because the model at the origin of R(N) is oversimplified. In particular, Sun is not a point and, in addition, it turns over itself. The gravific effects of this motion are major over the long term. It distorts the planetary trajectories up to put them in the equatorial solar plan. It reduces the eccentricity of the trajectories. It induces different effects depending on the rotation of planets on their trajectories as compared to that of Sun. Cf. [2] , chapter III.
Remark 3: The electron of a hydrogen atom is not durably stabilized on a Bohr’s orbit. On the contrary, a satellite is stabilized on a preferred trajectory, meaning that it cannot meet another preferred trajectory because of the following reason: the change of train of the hydrogen atom’s electron, i.e. the change of its principal quantum number, is caused by an exceptional U particle shock.
The change of the train, in an atom of the satellite of a gravific system star & satellite would be caused by an exceptional multiple shock of the M atoms which make the star. But M is is a large number and the probability of such a multiple shock is roughly nil. It is out of rule that an astronomer observe the exceptional passing of Saturn on a neighboring orbit, that of Jupiter or Uranus. Conversely, such a passing in a system of two isolated hydrogen atoms has a significant probability.
Remark 4: Over 184 potential satellites, we find 9. The 158 first ones have been absorbed by Sun and the 17 last ones are probably lost in the galaxy, virtually undetectable, on star-influenced trajectories.
4. Earth Satellites
As a supplement, we indicate in the following list the preferred distances of the earth satellites on a support between a = earth radius + 100 km and b = 5 times the distance between Earth and Moon. One may note that there are 9. We do not pretend that these distances define more stable orbits than the neighboring ones but they indicate that preferred distances exist. These considerations may have some practical utility given the multiplication of earth satellites aimed at diverse commercial purposes.
The ratio between Earth’s mass and that of an hydrogen atom is MT = 3.6 E51. The expressions of Rf and R(n) are those above-mentioned under the condition to replace M, the ratio between Sun’s mass ant that of a hydrogen atom, by MT.
Be A(j), j = 1, 2, ...N the satellite of rank j of the isolated system made by Earth and an hydrogen atom in the universal cloud.
Be R(j) the distance from Earth to the satellite A(j) with a circular orbit.
Be SLR the semi latus rectum of Moon’s orbit around Earth.
We present the list of A(j), R(j) ranked by increasing order of R(j) and under the condition a < R(j) < b.
We express R(j), not in astronomic unit AU but in earth radius ER. One also adds the height h of the orbit above Earth in km.
j = 120, R = 1.04 ER, height = 250 km
j = 121, R = 2.08 ER, height = 6 867 km
j = 122, R = 4.16 ER, height = 20 100 km
j = 123, R = 8.31 ER, height = 46 566 km
j = 124, R = 16.6 ER, height = 99 499 km
j = 125, R = 33.3 ER, height = 205 365 km
j = 126, R = 66.5 ER, height = 417 097 km
j = 127, R = 133. ER, height = 840 560 km
j = 128, R = 266. ER; height = 1 687 487 km
Moon’s rank is j = 126, calculated R = 66.5 ER versus observed SLR = 63.7 ER.
Remark: Moon is Earth’s only natural satellite versus a potential of 9.
It should not be excluded that Earth have absorbed all potential natural satellites, in lower orbits than Moon, during its existence.
Earth is not an isolated celestial body and the lower the orbit’s height of an earth’ satellite, the greater Sun’s impact on its movement. For Moon, this impact is large. The 58 potential natural satellites, in higher orbit than Moon may have never made up, or may have been lost, either in the solar system or outside this system;
We do not pretend that artificial satellites which would be put into orbit at the above-mentioned h(j) heights would be advantaged in terms of stability of their trajectories. We only estimate that there are a few neighbor preferred heights likely to be discovered empirically.
NOTA: We will examine in another note, relative to electromagnetic waves, the link which seems to emerge between ru and α, i.e. between the common reach of the gravific and electromagnetic influences, reach often assimilated to the size of the universe, and the fine-structure constant α which commands Bohr’s radius. This link has long been noticed by physicists, and seen, absent any explanation, as a random coincidence. On the contrary, Francis Sanchez [3] puts it at the top of its views on the universe.
Pre-quantum physics gives an explanation.
Cite this paper
RaoulCharreton, (2015) The Lines of Lyman and the Titus-Bode Law Preferred Orbital of a Celestial Body. Journal of Quantum Information Science,05,109-113. doi: 10.4236/jqis.2015.53013
References
- 1. Charreton, R.L. (2011) A pre-Quantum Atomic Physics. Published online, 30 March 2010.
http://perso.numericable.fr/raoul.charreton/ - 2. Charreton, R.L. (2009) Revision of the Foundations of Quantum Mechanics and Gravitation. L’Harmattan, Paris.
- 3. Sanchez, F. (2004) An Holographic Cosmology.
http://lempel.pagesperso-orange.fr/francis_sanchez.htm


