Journal of Quantum Information Science
Vol.05 No.02(2015), Article ID:57074,12 pages
10.4236/jqis.2015.52008
Formal Verification of Robertson-Type Uncertainty Relation
Takaaki Masuhara, Toru Kuriyama, Masakazu Yoshida, Jun Cheng
Department of Intelligent Information Engineering and Sciences, Doshisha University, Kyoto, Japan
Email: masyoshi@mail.doshisha.ac.jp, jcheng@ieee.org
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 30 April 2015; accepted 8 June 2015; published 11 June 2015
ABSTRACT
Formal verification using interactive theorem provers have been noticed as a method of verification of proofs that are too big for humans to check the validity of them. The purpose of this work is to verify the validity of Robertson-type uncertainty relation toward verifying unconditional security of quantum key distributions. We verify the validity of the relation by using proof assistant Coq and it is turned out that the theorem regarding the relation formally holds. The source code for Coq which represents the validity of the theorem is printed in Appendix.
Keywords:
Formal Verification, Proof Assistant Coq, Uncertainty Relation

1. Introduction
Formal verification is a technique for verifying the validity of proofs in mathematics, algorithms, computer sys- tems, and so on. In the formal verification by using logical reasoning, interactive theorem provers (HOL [1] , ACL2 [2] , Isabelle [3] , Coq [4] , just to a name a few) are used for verifying mathematical proofs. In accordance with the Curry-Howard correspondence [5] , the validity is verified through coding of the proofs in functional languages.
Formal verification by using the interactive theorem provers has been noticed as a technique for verifying proofs of theorems which are too large for humans to check the validity. Such a theorem as the Feit-Thompson theorem (also known as the odd order theorem) [6] can be enumerated as an example. This theorem was proven in 1963. However, the verification of the validity of the proof was highly difficult at 1980s [7] since its total number of pages are about 300. Gonthier et al. [8] verified the proof by using SSReflect which is an extension of the proof assistant Coq. The formalized theorem and lemmas which are formalized in the process of the veri- fication are utilized for the formalization of mathematical science. Therefore, the formal verification of rela- tively small lemmas which are used for large proofs is useful as a library for the verification of the other large proofs.
The formal verification is considered valid at information theory which is a branch of mathematical science. Affeldt et al. [9] formally verify basic definitions and theorems in information theory by using SSReflect, and also Shannon’s channel coding theorem and source coding theorem [10] which are famous theorems of all results of information theory. These formalized theorems are valuable not only toward the formally verification of integrity between coding and decoding algorithms and the software implemented ones, but also further facilitating of the formal verification by utilizing the formalized types.
In quantum information theory, the axioms of quantum physics are described mathematically [11] . Therefore, the formal verification can be applied to verifying the validity of quantum information theory. In this work, we verify the validity of uncertainty relation toward verifying unconditional security of quantum key distributions and encouraging the formal verification of large proofs in quantum information theory. Specifically, we verify the validity of Robertson-type uncertainty relation [12] by using the proof assistant Coq.
This paper is organized as follows. In Section 2, we review the theorem regarding Robertson-type uncertainty relation and its mathematically proof. In Section 3, we formally verify the validity of the theorem with Coq. In Section 4, this paper is summarized. Coq source code is printed in Appendix.
2. Robertson-Type Uncertainty Relation
Robertson-type uncertainty relation imposes a restriction on probability distributions of measurement outcomes with observables. In this type, uncertainty of the measurement is characterized by standard deviation of the dis- tribution.
In quantum information theory, a quantum system and a quantum pure state in the system are regarded in the same light as a Hilbert space and a unit vector in the space, respectively. In addition, an observable is regarded as an Hermitian operator on the Hilbert space. Let 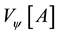 be variance of outcomes which are obtained by measuring a quantum system in a quantum state
be variance of outcomes which are obtained by measuring a quantum system in a quantum state 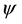 with an observable A. Then,
with an observable A. Then,
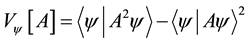 (1)
(1)
holds. Standard deviation of the outcomes  is defined as
is defined as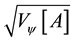 . The following theorem was given by Robertson [12] .
. The following theorem was given by Robertson [12] .
Theorem 1 ( [9] [12] ). For two observables A, B, and a quantum state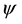 ,
,
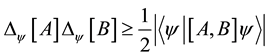 (2)
(2)
holds, where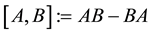 .
.
Proof. We observe 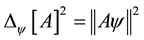 and
and 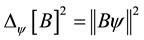 from the definition of standard deviation and
from the definition of standard deviation and
Hermiticity of the observable. 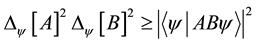 holds from the Schwarz inequality
holds from the Schwarz inequality
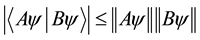 . We obtain
. We obtain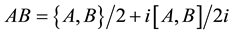 , where
, where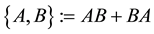 . We observe
. We observe
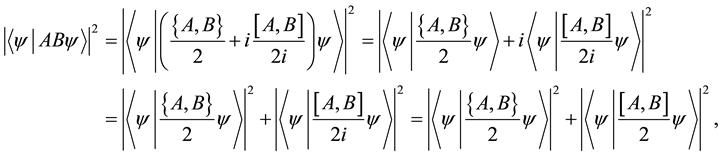
where we thank to Hermiticity of 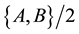 and
and
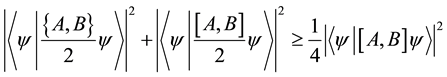

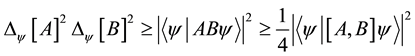
A relation between two observables represented by Equation (2) is called Robertson-type uncertainty relation. The right-hand side of the inequality always takes 0 if the observables are commutative. Therefore, both of standard deviations of the observables may take 0. On the other hand, for non-commutative observables, the right-hand side of the inequality dose not take 0. Then, both of standard deviations of the observables dose not take 0. This implies that Equation (2) is a tradeoff between uncertainties of the observables. In this case, the uncertainty is characterized by standard deviation.
The relation between the non-commutative observables often plays crucial role in discussion of unconditional security of quantum key distributions. In BB84 [13] which is the most famous quantum key distribution protocol, eigenstates of non-commutative observables 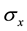
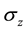








3. Formal Verification of Robertson-Type Uncertainty Relation
In this section, we verify the validity of Robertson-type uncertainty relation by using the proof assistant Coq. We define types as follows:
・ C: a type of a complex number
・ Vec C n: a type of an n-dimensional complex vector
・ UnitVec C n: a type of an n-dimensional complex unit vector
・ Mat C v: a type of a v = 
・ HMat v: a type of a v = 
We define functions as follows:
・ var: takes a pair of a variable of UnitVec C n and a variable of HMat v and returns variant with respect to the variables (see Equation (1))
・ cabs: takes a variable of C and returns absolute value of it
・ mMinus: takes a pair of variables of Mat C v and returns addition of them
・ mMinus: takes a pair of variables of Mat C v and returns subtraction of them
・ mMult: takes a pair of variables of Mat C v and returns product of them
・ innerProd: takes a pair of variables of Vec C n and returns inner product of them
・ mvMult: takes a pair of a variable of Mat C v and a variable of Vec C n and returns product of them
Theorem 2. We declare a formalized statement of Robertson-type uncertainty relation in Coq:
Theorem RobertsonUR:
forall (n : nat) (v : mlenghts n) (A B: HMat v) (psi : UnitVec C n),
(sqrt (var psi A)) * (sqrt (var psi B)) >=
(1/2) * (cabs ( innerProd psi (mvMult (mMinus (mMult A B) (mMult B A)) psi))).
Before giving the formally proof described by Coq, we show the broad outlines of it. Firstly, we define the types and the functions in linear algebra. The types and functions are already shown above. The next step is to obtain subgoals through applying small lemmas to some inequalities. The subgoals are formally verified through interactive proof sessions. Finally, we complete the verification of the the theorem regarding Robertson-type uncertainty relation when we have no new subgoals.
Proof. We execute the above statement and obtain a response from Coq:
1 subgoals
______________________________________(1/1)
forall (n : nat) (v : mlengths n) (A B : HMat v) (psi : UnitVec),
sqrt (var psi A) * sqrt (var psi B) >=
1/2* cabs (innerProd psi (mvMult (mMinus (mMult A B) (mMult B A)) psi))
For the above subgoal (statement), a command called tactic is inputted and executed, then, new subgoal which is rewritten according to the tactic is obtained as a response from Coq. We prove the statement through interactive proof sessions until there no exist new subgoals (for complete Coq source code, see Appendix).
We input the following tactic and execute it:
intros.
where intros is a tactic which adds a condition described by universal quantifier to preconditions. Then, we get the following response from Coq:
1 subgoals
n : nat
v : nlengths n
A : HMat v
B : HMat v
psi : UnitVec C n
______________________________________(1/1)
sqrt (var psi A) * sqrt (var psi B) >=
1/2* cabs (innerProd psi (mvMult (mMinus (mMult A B) (mMult B A)) psi))
For readability, 
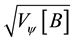
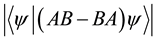
set ( a := sqrt (var psi A) ).
set ( b := sqrt (var psi B) ).
set ( c := (cabs (innerProd psi (mvMult (mMinus (mMult A B) (mMult B A)) psi)))).
Then, we get the following response from Coq:
1 subgoals
n: nat
v: mlengths n
A: HMat v
B: HMat v
psi: UnitVec C n
a:= sqrt (var psi A) : R
b:= sqrt (var psi B) : R
c:= cabs (innerProd psi (mvMult (mMinus (mMult A B) (mMult B A)) psi)):R
______________________________________(1/1)
a * b >= 1/2 * c
Hereafter, we show only subgoals which are responses from Coq. 
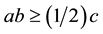
replace ( a * b >= 1 / 2 * c ) with ( (a * a) * (b * b) >= (1/4) * (c * c) ).
Then, we get the following response from Coq:
______________________________________(1/2)
a * a * (b * b) >= 1 / 4 * (c * c)
______________________________________(2/2)
(a * a * (b * b) >= 1 / 4 * (c * c)) = (a * b >= 1 / 2 * c)
For proving the inequality


transitive relation
to the preconditions by using a tactic assert:
assert ( a * a * (b * b) >=
(cabs ( innerProd psi (mvMult (mMult A B ) psi))) *
(cabs ( innerProd psi (mvMult (mMult A B ) psi))) /\
(cabs ( innerProd psi (mvMult (mMult A B ) psi))) *
(cabs ( innerProd psi (mvMult (mMult A B ) psi)))
>= (1 / 4) * (c * c) -> a * a * (b * b) >= 1 / 4 * (c * c)).
For proving the transitive relation
lemma R_leq_eq2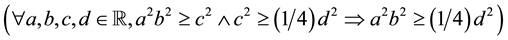
apply R_leq_eq2.
Then, we get the following response from Coq:
H : a * a * (b * b) >=
cabs (innerProd psi (mvMult (mMult A B) psi)) *
cabs (innerProd psi (mvMult (mMult A B) psi)) /\
cabs (innerProd psi (mvMult (mMult A B) psi)) *
cabs (innerProd psi (mvMult (mMult A B) psi)) >= 1/4 * (c*c)
-> a * a * (b * b) >= 1/4 * (c*c)
______________________________________(1/2)
a * a * (b * b) >= 1 / 4 * (c * c)
______________________________________(2/2)
(a * a * (b * b) >= 1 / 4 * (c * c)) = (a * b >= 1 / 2 * c)
Accordingly, the inequality which was performed with assert is added to the precondition as an assumption H. The assumption H is applied to the subgoal for proving
apply H.
We input a tactic split to split 
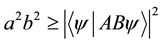

split.
For proving
apply RUR_Var_geq_InnerProd.

set ( d := cabs ( innerProd psi (mvMult (mMult A B ) psi)) ).
We get the following response from Coq:
______________________________________(1/2)
d * d >= 1 / 4 * (c * c)
______________________________________(2/2)
(a * a * (b * b) >= 1 / 4 * (c * c)) = (a * b >= 1 / 2 * c)
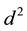
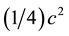
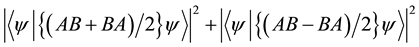
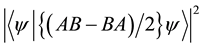
replace ( d * d ) with ((((1/2) * (cabs ((innerProd psi (mvMult (mPlus
(mMult A B) (mMult B A) ) psi))))) * ((1/2) * (cabs ( (innerProd psi (mvMult
(mPlus (mMult A B) (mMult B A) ) psi)))))) + (( (1/2) * (cabs ( (innerProd psi (mvMult
(mMinus (mMult A B) (mMult B A)) psi))))) * ((1/2) * (cabs ( (innerProd psi (mvMult
(mMinus (mMult A B) (mMult B A)) psi))))))).
replace ((1/4) * (c * c)) with (((1/2) * (cabs ((innerProd psi
(mvMult (mMinus (mMult A B) (mMult B A)) psi))))) * ((1/2) *
(cabs ((innerProd psi (mvMult (mMinus (mMult A B) (mMult B A)) psi)))))).
For proving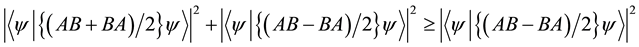
Plus_geq 
apply Square_Plus_geq.
For proving 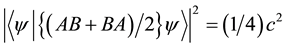

we apply RUR_eq_AB_0 and RUR_eq_AB_1 as follows:
apply RUR_eq_AB_0. apply RUR_eq_AB_1.
Then, we get the following response from Coq:
______________________________________(1/1)
(a * a * (b * b) >= 1 / 4 * (c * c)) = (a * b >= 1 / 2 * c)
For proving
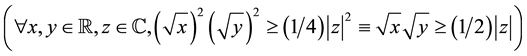
apply R_leq_eq.
Then, we get the following response from Coq:
No more subgoals.
All of the subgoals are proven. Input Qed and end the proof:
Qed.
The validity of Robertson-type uncertainty relation is verified formally.
4. Conclusion
In this work, we verified formally the validity of Robertson-type uncertainty relation by using the proof assistant Coq. We expect that the formalized theorem utilizes for facilitating the formal verification of the other theorems in quantum information theory. In future work, we will verify entropic uncertainty relation and the information disturbance theorem toward verifying unconditional security of quantum key distributions formally.
Acknowledgements
This work was partly supported by JSPS KAKENHI (24300030) Grant-in-Aid for Scientific Research (B), and MEXT-Supported Program for the Strategic Research Foundation at Private Universities (2014-2018, S1411030).
References
- Gordon, M.J.C. (1986) Why Higher-Order Logic Is a Good Formalism for Specifying and Verifying Hardware. In: Milne, G.J. and Subrahmanyam, P.A., Eds., Proceedings of the 1985 Edinburgh Workshop on VLSI, North-Holland, 153-177.
- Boyer, R.S., Moore, J.S. and Kaufmann, M. (1996) ACL2 Version 7.0. http://www.cs.utexas.edu/users/moore/acl2/
- University of Cambridge Computer Laboratory (1989) Isabelle. http://isabelle.in.tum.de/
- INRIA (1985) The Coq Proof Assistant. http://coq.inria.fr/
- Heine, M., Sørensen, B. and Urzyczyn, P. (2006) Lectures on the Curry-Howard Isomorphism. Warsaw University, Poland.
- Feit, W. and Thompson, J.G. (1963) Solvability of Groups of Odd Order. Pacific Journal of Mathematics, 13, 775- 1029. http://dx.doi.org/10.2140/pjm.1963.13.775
- Bender, H. and Glaubernan, G. (1995) Local Analysis for the Odd Order Theorem. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511665592
- Gonthier, G., Asperti, A., Avigad, J., Bertot, Y., Cohen, C., Garillot, F., Roux, S.L., Mahboubi, A., O’Connor, R., Biha, S.O., et al. (2013) A Machine-Checked Proof of the Odd Order Theorem. Lecture Notes in Computer Science, 7998, 163-179. http://dx.doi.org/10.1007/978-3-642-39634-2_14
- Affeldt, R., Hagiwara, M. and Sénizergues, J. (2014) Formalization of Shannon’s Theorems. Journal of Automated Reasoning, 53, 63-103. http://dx.doi.org/10.1007/s10817-013-9298-1
- Shannon, C.E. (1948) A mathematical Theory of Communication. Bell System Technical Journal, 27, 379-423. http://dx.doi.org/10.1002/j.1538-7305.1948.tb01338.x
- Hayashi, M., Ishizaka, S., Kawachi, A., Kimura, G. and Ogawa, T. (2014) Introduction to Quantum Information Sci- ence. Springer.
- Robertson, H.P. (1929) The Uncertanty Principle. Physical Review, 34, 163-164. http://dx.doi.org/10.1103/PhysRev.34.163
- Bennett, C.H. and Brassard, G. (1984) Quantum Cryptography: Public Key Distribution and Coin Tossing. Proceedings of IEEE International Conference on Computers Systems and Signal Processing, Bangalore, 175-179.
- Biham, E., Boyer, M., Boykin, P.O., Mor, T. and Roychowdhury, V. (2000) A Proof of the Security of Quantum Key Distribution. Proceedings of 32nd Annual ACM Symposium on the Theory of Computing, New York, 715-724.
- Miyadera, T. and Imai, H. (2006) Information-Disturbance Theorem for Mutually Unbiased Observables. Physical Review A, 73, Article ID: 042317. http://dx.doi.org/10.1103/PhysRevA.73.042317
- Miyadera, T. and Imai, H. (2007) Information-Disturbance Theorem and Uncertainty Relation. http://arxiv.org/abs/0707.4559
- Maassen, H. and Uffink, J.B.M. (1988) Generalized Entropic Uncertainty Relations. Physical Review Letters, 60, 1103. http://dx.doi.org/10.1103/PhysRevLett.60.1103
- Krishna, M. and Parthasarathy, K.R. (2002) An Entropic Uncertainty Principle for Quantum Measurements. Sankhya: The Indian Journal of Statistics, Series A, 64, 842-852.
Appendix: Coq Source Code






